提炼三角精髓放飞数学思想

■李 勇

三角函数中蕴含了许多数学思想,数学学习的精髓主要是思想方法的学习。同学们在掌握其基础知识的同时,还应注意数学思想的提炼、总结。那么,在三角函数中有哪些思想方法呢? 下面详细介绍,供同学们参考。

一、函数与方程思想

例1 已知角α的终边经过点P(5t,5t+1),且,求t的值。

分析:欲求t的值,需找出关于α的等式关系,利用三角函数的定义即可求解。

评注:方程思想就是用方程的观点分析所求的量,通过建立等量关系,然后解方程(组)使问题得到解决。

二、整体思想

例2 设函数f(x)=asin1000·,其中a,b,α,β为非零实数,已知f(2011)=-9,求f(2009)的值。

分析:观察题设及所求式子的特点,可采用整体代入法求解。

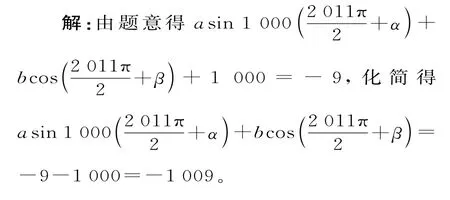
评注:利用整体思想解决问题时,要把握问题的全局,认清问题中相关元素的联系,从整体上利用条件进行简化求解。

三、正难则反思想

例3 将函数f(x)=Acos(ωx+φ)+B的图像上每一点的纵坐标伸长到原来的2倍,将横坐标缩短到原来的,再将整个图像沿x轴向左平移个单位,沿y轴向下平移1个单位,可得函数y=2sinx的图像,则原来的函数f(x)=____。

分析:因为三角变换具有可逆性,所以从结论反推,则简单易行。

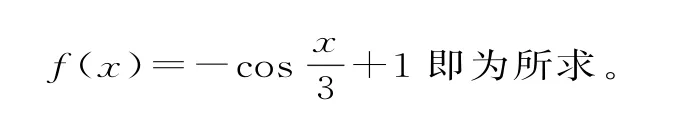
评注:利用正难则反的思想,反向思考问题,使得问题顺利获解。

四、数形结合思想

例4 方程sin2x=sinx在区间(0,2π)内的解的个数是____。

分析:在同一坐标系内分别作出函数y=sin2x和y=sinx的图像,由图像的交点个数判断方程解的个数。

解:在(0,2π)内,作出函数y=sin2x和y=sinx的图像,如图1所示。

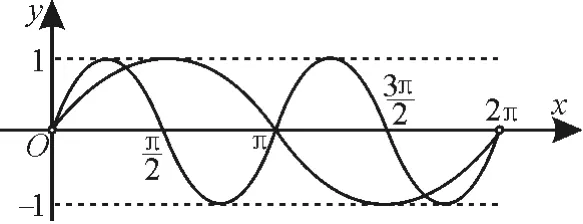
图1

在(0,2π)内的交点个数就是方程解的个数。因为两个图像共有3 个交点,所以原方程解的个数是3。

评注:方程f(x)=g(x)的实根个数就是函数y=f(x)和函数y=g(x)的图像的交点个数。

五、分类讨论思想

六、转化与化归思想

分析:由于条件比较复杂,涉及α+β,α-β,2α,2β等角,所以可考虑先将条件化简,得到关于α,β的三角函数,再逐步向条件靠近。

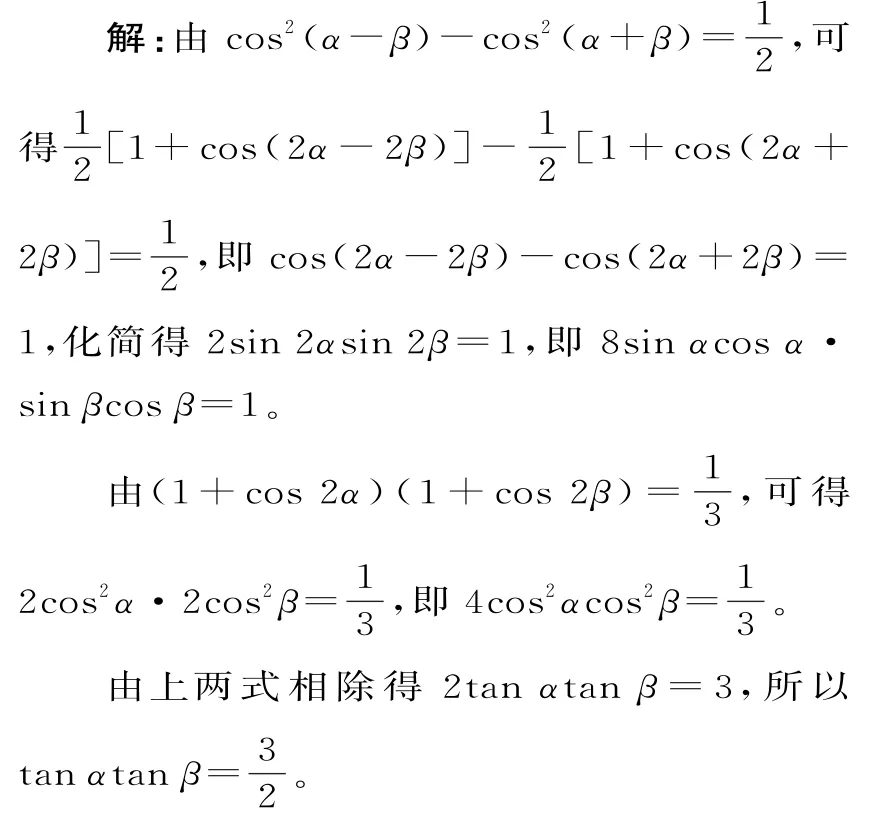
评注:通过化繁为简,使原来不易看到的关系显露出来,这是问题转化的原则之一。