三角函数常见典型考题赏析

■赵 昆

三角函数是每年高考的热点之一,高考主要考查三角函数的图像与性质、三角函数的化简与求值等。下面就三角函数常见典型考题,进行实例剖析,供大家学习与参考。

题型1:终边相同的角

终边相同的角之间相差360°的整数倍;终边在同一直线上的角之间相差180°的整数倍;终边在相互垂直的两直线上的角之间相差90°的整数倍。

例1 (1)把-1480°写成α+2kπ(k∈Z)的形式,其中0≤α≤2π。

跟踪训练1:已知角α=2025°。

(1)将角α改写成β+2kπ(k∈Z,0≤β<2π)的形式,并指出角α是第几象限的角。

(2)在区间[-5π,0)上找出与角α终边相同的角。

提示:(1)因为,又是第三象限角,所以α是第三象限角。

题型2:象限角

判断角α是第几象限角的常用方法:将α写成β+k·360°(其中k∈Z,β在0°～360°范围内)的形式,观察角β的终边所在的象限即可。由α所在的象限确定2α所在的象限时,应注意2α可能不再是象限角,对此特殊情况应特别指出,如α=135°,而2α=270°就不再是象限角。

例2 若α是第二象限角,则180°-α是( )。

A.第一象限角 B.第二象限角

C.第三象限角 D.第四象限角

解:α为第二象限角,不妨取α=120°,则180°-α为第一象限角。应选A。

跟踪训练2:在0°～360°范围内,找出与下列各角终边相同的角,并判断它们是第几象限角。

(1)-150°;(2)650°;(3)-950°15′。

提示:(1)因为-150°=-360°+210°,又210°是第三象限角,所以-150°是第三象限角。

(2)因为650°=360°+290°,又290°是第四象限角,所以650°是第四象限角。

(3)因为-950°15′=-1080°+129°45′,又129°45′是第二象限角,所以-950°15′是第二象限角。

题型3:三角函数角的判断

当角θ的终边在不同象限时,其三个三角函数值的符号会发生变化,记忆的口诀是“全正切余”,即第一象限全为正,第二象限正弦为正,第三象限正切为正,第四象限余弦为正。

例3 若sinαtanα<0,且,则角α是( )。

A.第一象限角 B.第二象限角

C.第三象限角 D.第四象限角

解:因为,所以cosα<0。又因为,所以sinα<0,所以角α为第三象限角。应选C。

跟踪训练3:“θ为第一或第四象限角”是“cosθ>0”的( )。A.充分不必要条件B.必要不充分条件C.充要条件

D.既不充分也不必要条件

提示:当θ为第一或第四象限角时,cosθ>0,所以“θ为第一或第四象限角”是“cosθ>0”的充分条件。当cosθ>0时,θ为第一或第四象限角或x轴正半轴上的角,所以“θ为第一或第四象限角”不是“cosθ>0”的必要条件。故“θ为第一或第四象限角”是“cosθ>0”的充分不必要条件。应选A。

题型4:sinα±cosα 与sinαcosα 关系的应用

sinα+cosα,sinα-cosα,sinαcosα这三个式子,已知其中一个,可以求其他两个,即“知一求二”,它们之间的关系是(sinα±cosα)2=1±2sinαcosα。求sinα+cosα或sinα-cosα的值,要注意根据角α所在的象限判断它们的符号。

题型5:已知tanα,求关于sinα 与cosα的齐次式的值

题型6:诱导公式的应用

诱导公式的应用策略:将已知角化为k·360°+α(k为 整 数,0°≤α<360°)或2kπ+β(k为整数,0≤β<2π)的形式;将原三角函数值化为角α的同名三角函数值,借助特殊角的三角函数值或任意角的三角函数的定义达到化简求值的目的。对于角(k∈Z)”的变换遵循“奇变偶不变,符号看象限”的法则。“奇变偶不变”是指“当k为奇数时,正弦变余弦,余弦变正弦;当k为偶数时,函数名不变”。“符号看象限”是指“在角α的三角函数值前面加上当α为锐角时,原函数值的符号”。

例6 已知角α终边上一点P(-4,3),则的值为_____。

解:因为P(-4,3)是角α终边上一点,所以

题型7:三角函数的奇偶性与周期性的应用

解决三角函数的奇偶性与周期性问题的方法:利用函数的周期性,把x+nT(n∈Z)的函数值转化为x的函数值;利用奇偶性,找到-x与x的函数值的关系,从而解决求值问题。若f(x+t)=f(x),则函数周期为t;若f(x+t)=-f(x),则函数周期为2t;若,则函数周期为2t;若,则函数周期为2t。

例7 下列函数中,不是周期函数的是( )。

A.y=|cosx| B.y=cos|x|

C.y=|sinx| D.y=sin|x|

解:函数y=|cosx|是周期函数,排除A。函数y=cos|x|=cosx是周期函数,排除B。函数y=|sinx|是周期函数,排除C。函数y=sin|x|不是周期函数,D 满足题意。应选D。

题型8:三角函数单调性的应用

求正、余弦函数有关的单调区间,可利用正、余弦函数的图像,结合它们的单调区间求解。确定函数y=Asin(ωx+φ)(A>0,ω>0)单调区间的方法:采用换元法整体代换,将ωx+φ看作一个整体,令z=ωx+φ,通过求y=Asinz的单调区间而求出此函数的单调区间,注意当ω<0 时,可利用诱导公式将x的系数转变为正数。比较三角函数值大小的步骤:把异名函数化为同名函数,利用诱导公式把角化到同一单调区间上,利用三角函数的单调性比较大小。

例8 已 知 函 数f(x)=sin（ωx+）(ω>0),对 任 意x∈R,都 有f(x)≤,且f(x)在区间上不单调,则ω的最小值是( )。

A.1 B.3 C.5 D.7

解:由题意得是函数f(x)的最大值,所以,k∈Z,即ω=6k+1,k∈Z。

因为ω>0,所以取k=0,可得ω=1,且上单调递增,这时不符合题意;

取k=1,可得ω=7,且f(x)=sin（7x+）,这时符合题意。

故ω的最小值为7。应选D。

跟踪训练8:函数f(x)=cos(x+θ)在[0,π]上为增函数,则θ的值可以是( )。

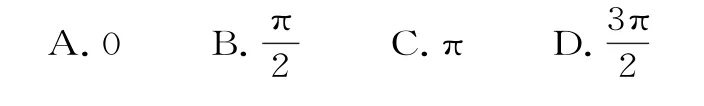
提示:对于A,f(x)=cosx,由余弦函数的性质知f(x)在[0,π]上为减函数,排除A。对于B,在[0,π]上先减后增,排除B。对于C,f(x)=cos(x+π)=-cosx,由余弦函数的性质知f(x)在[0,π]上为增函数,C 成立。对于D,在[0,π]上先增后减,排除D。应选C。

题型9:正切函数的图像与性质的应用

题型10:和角公式与差角公式的应用

四个 公 式C(α±β)、S(α±β),虽 然 形 式 不 同、结构不同,但它们的本质是相同的,其内在联系为-β)。对于公式C(α-β)与C(α+β),可记为“同名相乘,符号相反”,对于公式S(α-β)与S(α+β),可记为“异名相乘,符号相同”。使用和差角公式时,不仅要会正用,还要会逆用,如化简sinβ·cos(α+β)-cosβsin(α+β)时,不要将cos(α+β)和sin(α+β)展开,应采用整体思想,作如下变形:sinβcos(α+β)-cosβ·sin(α+β)=sin[β-(α+β)]=sin(-α)=-sinα。对 于 公 式T(α+β),T(α-β),tanα·tanβ,tanα+tanβ(或tanα-tanβ),tan(α+β)(或tan(α-β)),三者可“知二求一”。

例10 求值:

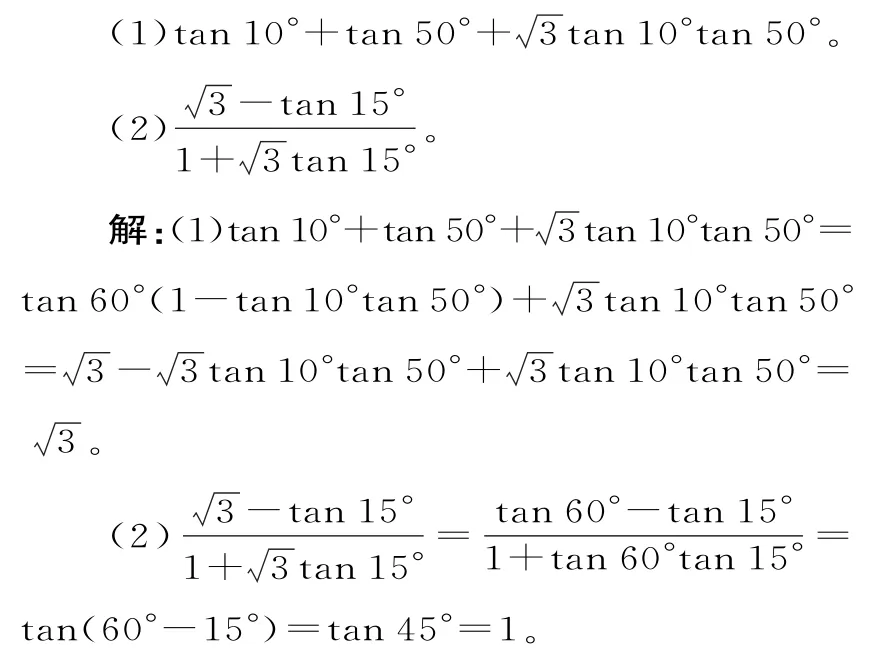
跟踪训练 10:下列化简正确的是( )。

题型11:给值(或式)求值

对于给值求值问题,当“已知角”有两个时,“所求角”一般表示为两个“已知角”的和或差的形式;当“已知角”有一个时,应着眼于“所求角”与“已知角”的和或差的关系,应用诱导公式把“所求角”变成“已知角”。

题型12:给值求角

给值求角的实质是转化为给值求值,先求角的某一三角函数值,再求角的范围,最后确定角的大小。

例12 已知sin(α+β)=sinα-sinβ,若,且β∈（0,π ）,则β=( )。

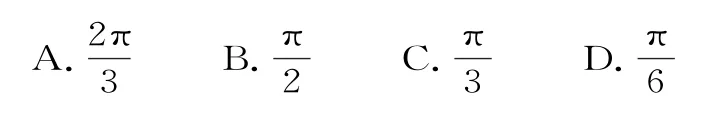
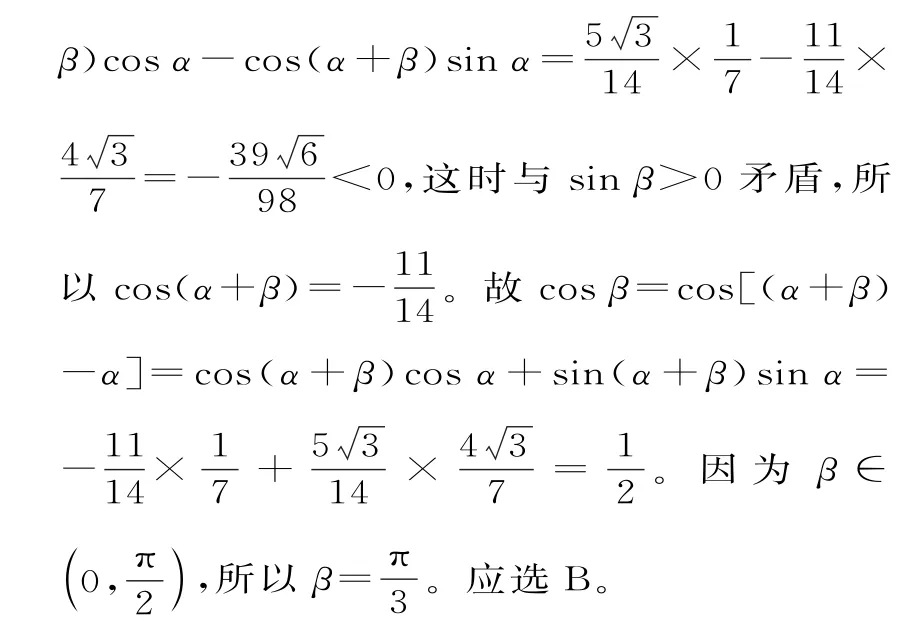
题型13:二倍角公式的应用

公式的正用:从条件出发,顺着问题的线索,以“展开”公式的方式使用。公式的逆用:逆向转换,应用时要求对公式特点有一个整体感知,主要形式有2sinαcosα=sin2α,等。公式的变形应用:将公式进行简单等价变形后,利用其新形式,主要形式 有1+cos2α=2cos2α,1-cos2α=

题型14:函数y=Asin(ωx+φ)的图像与性质的应用

给出y=Asin(ωx+φ)的图像的一部分,确定A,ω,φ的三种方法:先从图像上可直接确定A和ω,再选取五点法中的“第一零点”代入“ωx+φ=0”(要注意正确判断哪一点是“第一零点”),求得φ,或选取最大值点代入,k∈Z,选取最小值点代入,k∈Z,求得φ;结合五点法,将特殊点代入函数式,可以求得相关待定系数A,ω,φ,这里需要注意的是,要认清所选择的点属于五点法中的哪一点;利用逆向思维的方法,先确定函数的基本解析式y=Asinωx,再根据图像平移、伸缩规律,确定相关的参数。

例14 已知函数f(x)=Asin(ωx+φ)的部分图像,如图1所示。

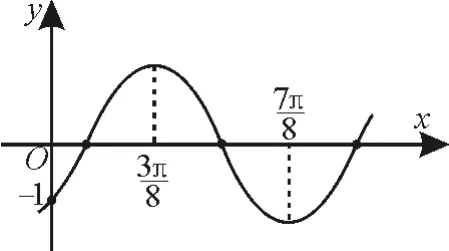
(1)求函数f(x)的解析式。

(2)将函数f(x)的图像向左平移个单位,再将图像上各点的横坐标伸长到原来的2倍(纵坐标不变)得到函数g(x)的图像,求函数g(x)在区间[0,π]上的值域。

解:(1)由图可知,,可得T=π,则ω=2,这时f(x)=Asin(2x+

图2

A.函数g(x)是奇函数

B.函数g(x)在区间[-2π,0]上是增函数

C.函数g(x)的图像关于点(3π,0)对称

D.函数g(x)的图像关于直线x=-3π对称