动态冲突搜索的多无人车路径规划算法
2023-12-20唐嘉宁陈云浩和雪梅闫搏远
唐嘉宁,颜 衡,陈云浩,和雪梅,闫搏远
(1.云南民族大学 电气信息工程学院, 昆明 650000; 2.云南民族大学 无人自主系统研究院, 昆明 650000)
0 引言
自1980年代,无人车开始进入人类的生活,无人车凭借高机动性、高性能、执行危险任务不会造成人员伤亡等优点被广泛应用于各种场景,为人类的生活、工作等提供了极大的便利[1]。但是在面对抢险救灾、重要目标搜索等时间要求高的任务时,单无人车受到载荷、能源条件的限制,难以在有限的时间内快速完成一些复杂的任务,因此,多无人车的协同是当前的一个研究热点。
为使多无人车能够快速应对紧急复杂的任务,需要快速生成连接无人车初始位置和目标位置的无碰撞路径,即多无人车路径规划(multi-UGV path finding)问题。多无人车路径规划问题是一个NP-hard问题,为多无人车规划出一组从已知起点到目标终点的无碰撞冲突最优路径。目前,关于多无人车路径规划的方法大多是基于A*[2-3]、人工势场[4]和Dijstra[5-6]等传统算法进行改进优化。Silver等[7]提出一种HCA*算法,根据预先定义的顺序依次规划无人车,当无人车找到目标路径时,此路径将被存储到全局保存表中,后续无人车在搜索路径时不会遍历先前发生冲突的位置。然而,随着无人车数量增加,状态空间呈指数级增长,在无人车数量多、地图较大的场景,可能无法在有限时间内找到最优解。
除了上述传统路径规划算法外,如蚁群算法[8]、遗传算法[9]等启发式算法也逐渐应用到了多无人车路径规划中。另外一些学者运用机器学习的方法解决多无人车路径规划问题,Xia等[10]将神经网络用于多无人车路径规划问题,以冲突半径和每个路径点到冲突中心的距离差作为神经网络的输入,把冲突和路径距离的加权作为神经网络的目标函数,输出一组规避冲突且使每一条路径距离总和最短的路径点。但是以上方法都存在计算量大,求解速度慢,容易陷入局部最优等缺点。
CBS算法[11-13]是一种用来求解多无人车路径规划问题最优解的框架,该算法通过底层搜索路径,顶层消除冲突实现多无人车路径规划问题的求解;Li等[12]提出了一种基于安全走廊约束的非线性优化CBS算法,为每辆无人车构建安全走廊,并对无人车的优先级进行排序;Sharon等[13]在CBS算法的基础上提出了一种MA-CBS(Meta-Agent CBS)算法,该算法不局限于单智能体的底层搜索,而是将有冲突的智能体合并为一个小组,相比CBS算法,计算速度提升了一个数量级;Barer等[14]提出的ECBS算法通过焦点搜索大幅度减少了运行时间;Andreychuk等[15]提出了时间连续的CBS算法(continous-time CBS,CCBS),将某个时刻的约束改为某个时间段内的约束;Li等[16]提出明确估计CBS(explicit estimation CBS,EECBS)算法,该算法的顶层搜索树的扩展由在线学习决定;Chan等[17]提出了增强并行CBS(ENHANCED PARALLEL CBS)算法,在ECBS的基础上采用多线程进行搜索,提高ECBS算法的效率;Li等[18]改进了CBS算法的顶层搜索,通过推理智能体之间的冲突关系提出了2种启发式,显著提高了成功率;乔乔等[19]将ECBS算法中的单向搜索改为双向搜索,以加快搜索速度。Li等[20]使用多邻域搜索对智能体集群进行重规划,解决了范围大的多智能体路径规划问题。
以上研究中对CBS算法的改进都存在搜索效率低以及生成的路径不符合运动学约束等问题,因此,本文在CBS算法的基础上,对底层搜索进行改进,提出了一种混合A*焦点搜索算法,使生成的路径更符合运动学约束;引入次优因子提高了CBS算法效率;并将路径距离加权系数和时间加权系数引入CBS算法的底层路径搜索中,以找到快且短的路径。
1 多无人车路径规划
1.1 问题描述
多无人车路径规划问题是由一组k个无人车{r1,r2,…,rk}与有向图G=(V,E)组成,每个无人车ri都有各自的起点si∈V和目标点gi∈V。在每个时间点t,无人车可执行一个移动到相邻顶点的动作或保持当前位置的等待动作,这2个动作的时间成本都是t0,但是路径距离成本只有无人车移动时才增加。目标是为多无人车找出一组从起点si到目标终点gi的无碰撞冲突最优路径,该路径不仅要满足路径距离成本最小,还要尽量满足时间成本累积小。
1.2 数学模型
(1)

(2)

(3)
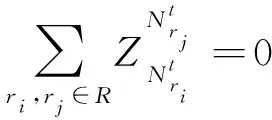
(4)
式(1)表示最小化多无人车路径总代价,Ci表示无人车ri的路径成本;式(2)表示一个目标点只能分配给一个无人车;式(3)表示一辆无人车只能对应唯一的目标点;式(4)表示不允许2辆无人车在同一时间出现在同一位置。
2 冲突搜索算法
冲突搜索(CBS)算法是求解多无人车路径规划问题的最优解算法框架。底层使用A*,Dijstra等普通算法进行单机路径搜索,为每辆无人车寻找各自的有效最优路径,但和传统A*算法不同的是:① 需要满足顶层搜索中添加的冲突规避约束;② 最优路径搜索不仅要考虑空间维度,还要考虑时间维度。
顶层遍历底层搜索的路径,检查路径之间是否存在冲突,如果存在冲突,则添加约束后重新进行底层搜索,直到所有路径没有冲突为止。
CBS中顶层搜索生成一棵二叉树(constarint tree,CT),CT中每个节点N都包含以下信息:
1) 对每辆无人车的约束集Ncon。CT中的根节点为一组空约束,子节点继承父节点的约束,且为一辆无人车增加一组新的约束。
2) 一组无人车的路径Nsol。该组路径通过底层搜索得到,每辆无人车ai的路径必须满足当前节点的Ncon。
3) 总成本Ncost。该值为Nsol中每辆无人车的路径成本总和。
以图1为例,图中无人车r1要移动到g1,无人车r2要移动到g2。
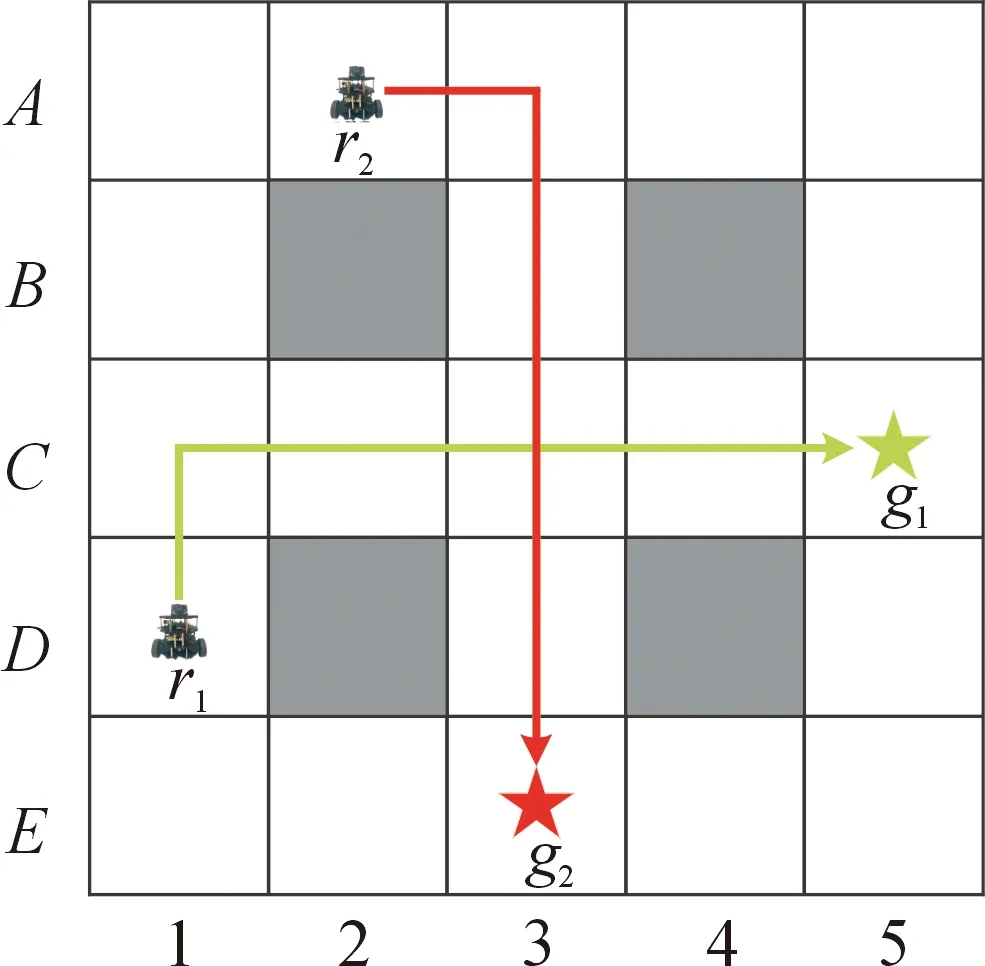
图1 多无人车路径示意图
底层搜索中两辆无人车各自的最优路径为r1:
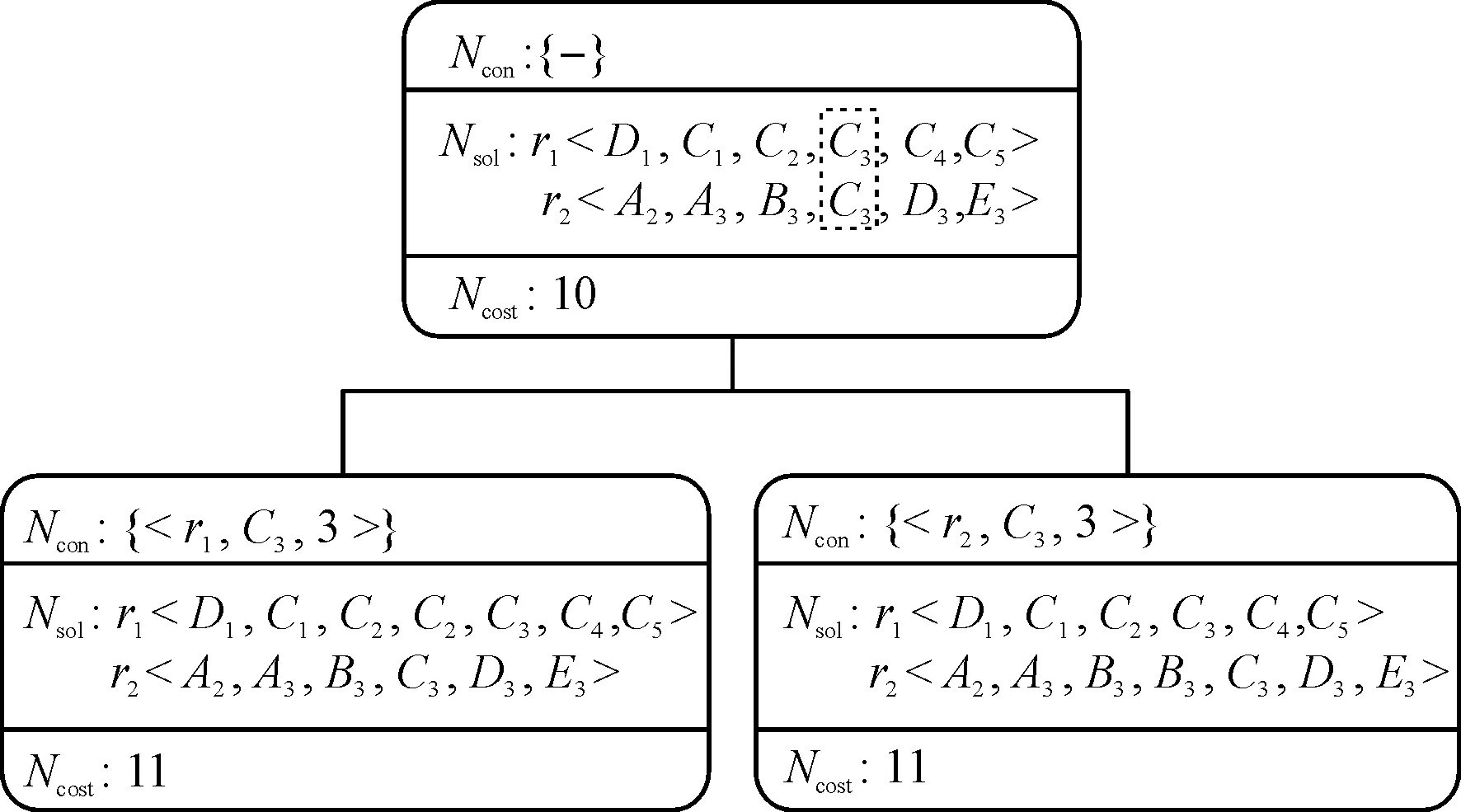
图2 冲突生成的二叉树示意图
3 动态冲突搜索算法
3.1 ECBS算法
CBS算法在顶层搜索检测到冲突时,会根据冲突生成2个子节点,并对2个子节点新增相应的约束,在底层路径搜索时,只需要找到满足约束的路径,这种盲目的搜索只能处理当前的冲突,新规划的路径还可能再次出现冲突,因此,增强的CBS(enhanced conflict-based search,ECBS)算法在CBS的框架基础上对2层搜索进行了优化。
ECBS算法与CBS算法相同,底层搜索每个无人车的路径,顶层消除无人车之间的冲突。不同的是ECBS在顶层和底层搜索中使用了焦点搜索,每次迭代不仅搜索一条最优的路径,而是搜索在恒定次优因子ω内的全部路径,大大降低冲突频率的发生,其基本流程如图3所示。

图3 搜索多无人车路径基本流程框图
焦点搜索生成2个节点列表:OPEN和FOCAL。OPEN列表是A*算法的常规列表,存储当前节点和所有邻居节点的集合;FOCAL列表是OPEN列表的子集,存放符合下面要求的节点:
FOCAL={n|n∈OPEN,f(n)≤ω·fmin(n)}
(5)
式中:n表示路径节点,fmin(n)为OPEN列表中代价估计的下界,ω为次优因子,FOCAL列表中所有路径节点的代价在ω·fmin(n)以内,FOCAL列表中的节点按照每个节点发生冲突的次数进行增序排列,用来判断节点扩展顺序的优先级。


3.2 混合A*搜索算法
ECBS算法虽然能够保证解决方案的同时提高搜索效率,但是在底层搜索时仍采用传统的A*算法,未考虑在实际应用场景中的运动学约束问题,本文结合传统A*算法,提出了在底层路径搜索中使用混合A*焦点搜索算法,使规划的路径符合无人车运动学约束,同时有效减少了冲突发生的概率,进而提高了算法搜索路径的速度。
传统A*算法的节点会选择周围4个或8个节点进行扩展,如图4(a),这种节点扩展方式只考虑位置,而忽略了方向角信息,因此不适合用在有运动学约束的无人车上。本文的混合A*算法在进行节点扩展时,需要考虑运动学约束,所以扩展的节点包含了方向角信息,通过对路径的曲率添加约束条件来满足无人车角速度的约束,图4(b)为混合A*节点扩展的基本方式。
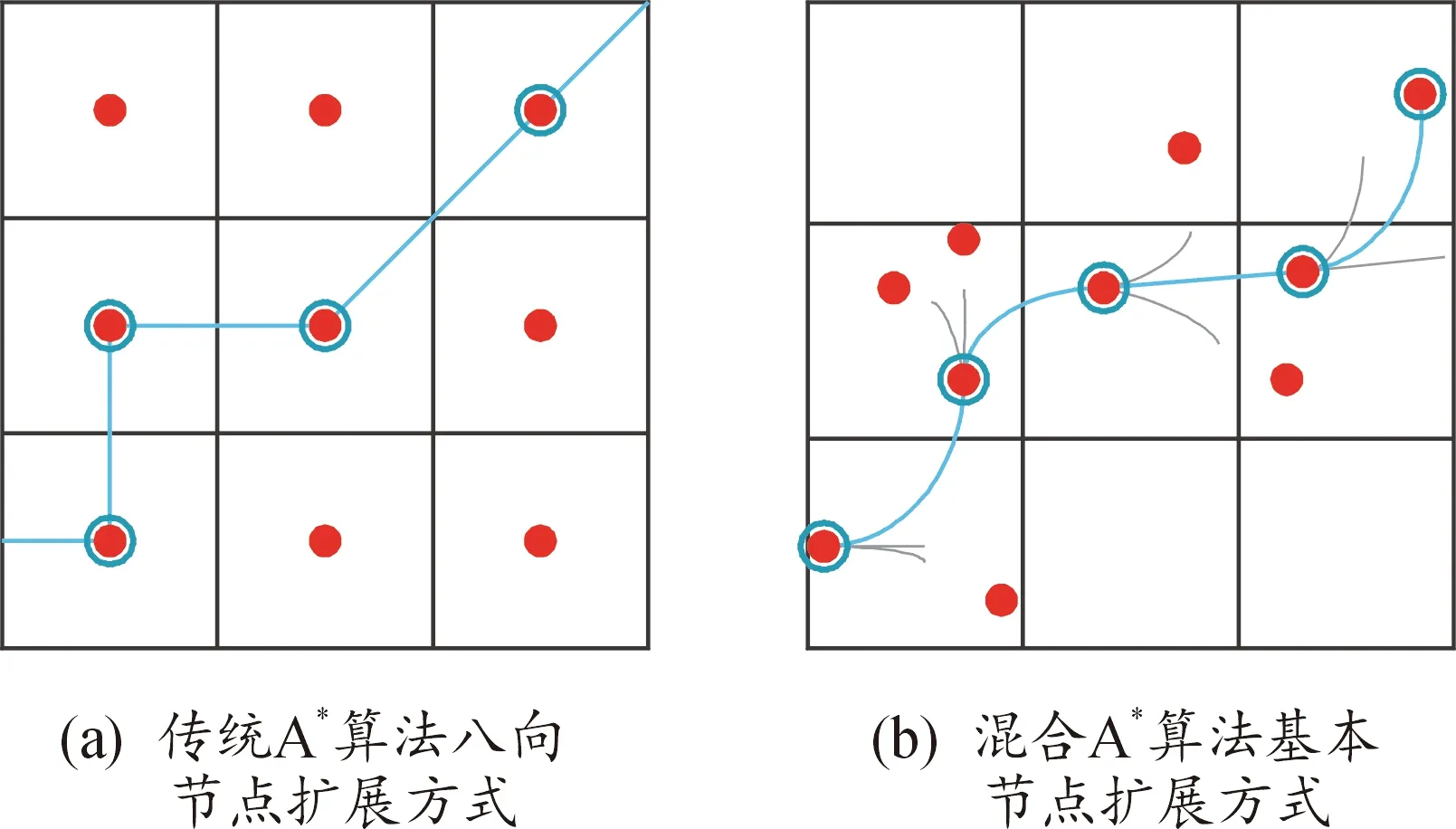
图4 节点扩展示意图
本文的混合A*继承了传统A*的一些思想,都会生成OPEN和CLOSE列表以及启发式函数f(n)=g(n)+h(n),其流程如图5所示。

图5 混合A*算法流程框图
混合A*算法中g(n)与传统A*相同,均为无人车实际行驶的距离,不过h(n)需要考虑的因素有很多,如转向角变化,因此本文中混合A*的启发式评估代价为
(6)
式中: (sx,sy)和(gx,gy)分别为当前节点n和目标节点的坐标值;kθ为偏航角的权重系数;θ为无人车当前位置的指向角度;θg为当前节点n指向目标节点的角度。
3.3 动态焦点搜索算法
在底层搜索中,将混合A*算法中OPEN列表中满足条件的次优子节点加入FOCAL列表中,并从FOCAL列表中选择要扩展的节点,当目标点出现在FOCAL列表某节点的搜索范围内停止搜索。因为混合A*生成的子节点并不一定位于栅格的顶点或中心位置,即同一栅格内可能有多个节点,因此,当同一栅格的2个子节点距离小于或等于2倍的无人车半径Ri时,才有可能发生冲突,否则两辆无人车可以同时出现在同一栅格。
混合A*焦点搜索算法在多无人车路径规划时,不仅能够规划出更符合运动学约束的平滑路径,还能减少冲突的发生,提高搜索路径的效率。
多无人车进行路径规划时,会为了找到最短路径需等待较长的时间,因此,不能仅用路径的长度作为衡量标准,尤其是在重要物资投送等对时间敏感度高的任务中,路径的时间成本同样重要,因此,本文将路径距离加权系数和路径时间加权系数代入函数中,使用公式(7)衡量多无人车路径的总成本,
(7)
式中:li表示无人车ri的路径距离;ti为无人车ri由起点到达目标点的时间;α和β分别为路径距离和时间的加权系数。
4 仿真实验及结果分析
4.1 仿真实验设置
为验证本文提出改进混合A*焦点搜索的有效性和可行性,采用ROS仿真平台,在一台ubuntu16.04,intel i5-12400@2.5 GHz处理器,运行内存16GB的集显台式机电脑上运行。对文献[12]的CBS算法和本文提出的动态CBS算法进行对照实验。在仿真中,使用八叉树地图表示环境的占用情况。其中无人车的参数设置如表1所示。

表1 无人车参数设置
4.2 算法性能对比
图6为本文方法20辆无人车在随机障碍物环境中、不同时间点运行的轨迹图,其中图6(a)和图6(d)分别为无人车初始时刻的位置和无人车行驶至目标点时的最终轨迹图。地图环境设置为8 m×8 m的正方形,环境里包含随机生成的12个0.3 m×0.3 m的正方形障碍物,每辆无人车的起点和目标点位置在实验开始之前给定,并保证不被障碍物占据。
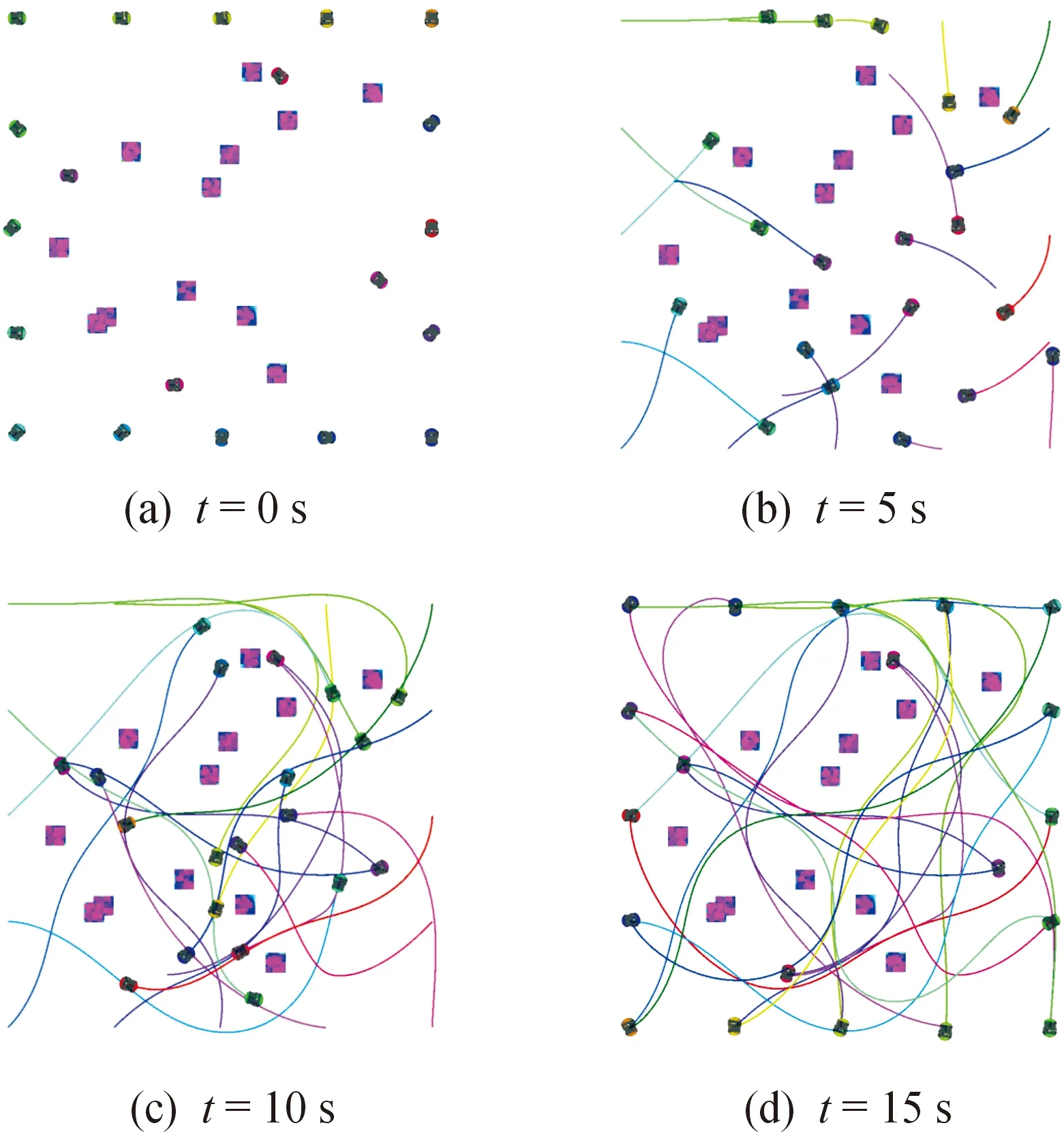
图6 随机障碍物环境20辆无人车不同时间点的轨迹
图7表示8辆无人车在算法改进前后求解的路径质量对比。
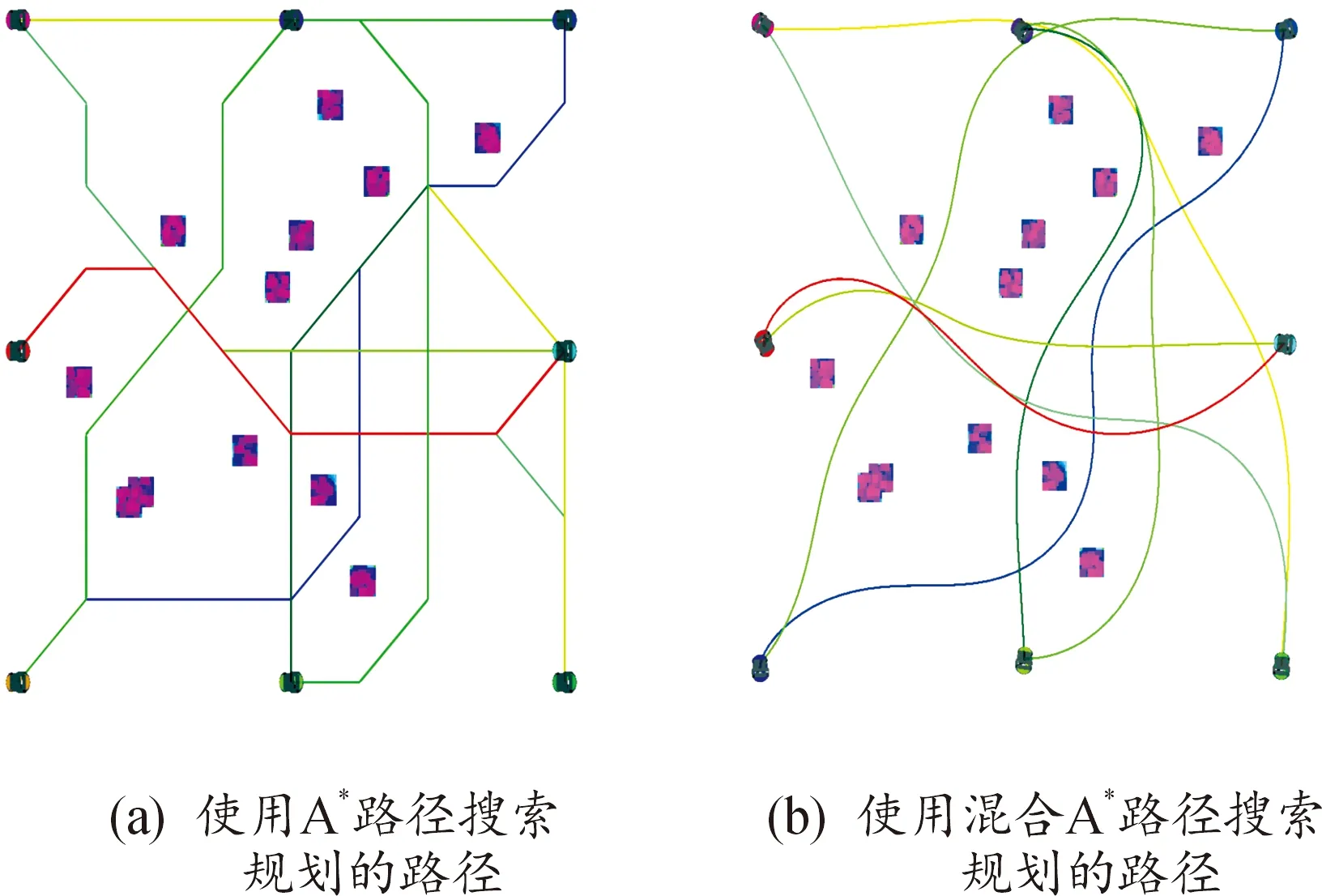
图7 CBS算法底层搜索使用A*路径搜索和混合A*路径搜索结果图
本文提出的算法能够有效提高多无人车路径的求解质量,主要体现在求解的路径更符合无人车运动学的约束,图7(a)为改进前的CBS算法在底层搜索中使用A*路径搜索,因为传统A*算法八向搜索和扩展的特性,无人车的路径为折线;图7(b)为本文改进后的CBS算法,在底层使用混合A*路径搜索,根据无人车转向角进行节点扩展,同时生成满足无人车运动学约束的轨迹,规划的路径是平滑曲线。同时无人车的路径重合部分也大幅减少,这也为之后的顶层冲突消解节省了时间。
为验证算法的效率,在相同的仿真环境中,分别对本文方法和前沿的ECBS算法各重复21次实验,记录每次实验结果并取平均值为最终的实验结果。图8为不同数量无人ECBS运行的时间曲线。
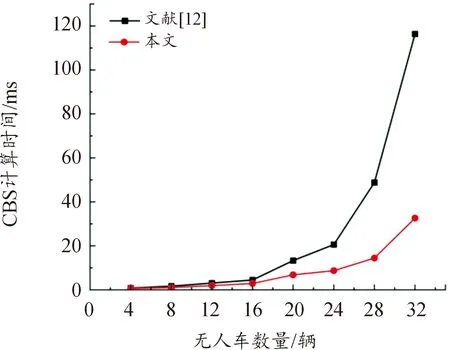
图8 算法计算时间曲线
与前沿的ECBS方法相比,本文提出的DCBS算法搜索的路径重合部分大幅度减少,配合次优路径策略和混合A*算法,无人车可选择的路径数量变多,无人车之间的冲突数量减少,计算速度整体提高。当无人车数量在4—16辆时,本文提出的算法计算时间减少了0.14~1.56 ms,相较于前沿的ECBS算法平均提高了31.98%;当无人车数量超过20时,计算速度的提升逐渐明显,本文提出的算法计算速度的提升均超过50%,尤其是在32辆无人车时,计算速度的提升最明显,计算时间缩短83.71 ms,计算速度提升了71.95%。实验数据表明:本文提出的DCBS算法在多无人车的路径规划速度上有明显提升,尤其是在无人车数量较多的情况下,提出的DCBS算法更具适用性。
为了验证本文提出的算法不仅在更短的时间内为多无人车规划出符合运动学约束的路径,且路径总成本也有降低,使用引入路径距离权重α和时间权重β的代价判别公式(7)对路径总成本进行衡量,其中距离权重和时间权重分别设置为0.2和0.1。图9为本文方法与前沿ECBS算法路径总成本曲线,因为无人车数量的增加,2种方法的路径总成本都在不断增加,但本文方法路径总成本普遍更低,路径总成本平均降低7.64%。在16辆和28辆无人车时,路径总成本降低最多,分别降低了10.52和10.92;在8辆无人车时,路径总成本虽然只降低了6.66,但是因为无人车数量少,路径总距离和时间都很短,路径总成本降低了18.91%,是本文实验中的成本降低率的最大值。实验数据表明:本文提出的DCBS算法有效降低了多无人车路径的总成本。

图9 路径成本曲线
5 结论
本文针对CBS算法在多无人车路径规划中存在求解效率低,求解路径不符合无人车运动学约束等问题,在CBS算法的基础上,提出了动态CBS(DCBS)算法,基于次优策略和路径平滑策略,在底层搜索中使用混合A*搜索算法并引入次优因子,提高了路径的规划速度,使规划的路径更符合运动学的约束;为了解决多车路径规划为了找到最短路径而等待时间过长的问题,引入路径距离加权系数α和时间加权系数β,平衡路径距离和时间的关系,以规划出快且短的路径。与前沿ECBS算法相比,本文提出的DCBS算法减少了多无人车路径规划的时间,规划出的路径更符合运动学约束,同时使整体路径代价减少。
本文研究的多无人车路径规划是二维平面路径规划,未来将以多无人机三维环境中的路径规划为重点展开研究。
