复杂轮廓膜式空气弹簧非线性结构参数统一模型
2023-12-18陈俊杰张盛蓬袁显举李国全
陈俊杰, 张盛蓬, 刘 昊, 袁显举, 李国全
(1. 江西理工大学 机电工程学院, 江西 赣州 341000; 2. 湖北汽车工业学院 汽车工程学院, 湖北 十堰 442002; 3. 广东溢康通空气弹簧有限公司技术中心, 广东 云浮 527300)
膜式空气弹簧(rolling lobe air spring, RLAS)刚度小,频率低,可通过设计合理的活塞轮廓形状获得理想的力学特性曲线,广泛应用于新能源乘用车、商用车、轨道车辆及空气悬浮座椅悬架中[1]。RLAS结构参数涵盖有效面积、有效面积变化率和有效体积、有效体积变化率四个参数,建立RLAS非线性结构参数统一模型是设计、优化空气弹簧力学性能的关键基础工作,对提升RLAS正向研发水平具有重要的理论意义和工程价值[2]。
袁春元等[3]采用有限元法建立了RLAS的静、动态特性有限元模型,研究了RLAS的力学特性。Fox等[4]研究了 RLAS 的结构参数建模,基于试验数据对RLAS有效面积、有效体积进行了等效处理,提出了由压缩空气模型、摩擦模型和阻尼模型并联而成的RLAS力学模型,但对于有效面积、有效体积等结构参数缺乏理论研究,仅通过试验数据获得。Quaglia等[5]对RLAS的有效面积和有效体积进行了试验,结果表明有效面积、有效体积仅是RLAS高度的函数。随后,陈燎等[6]通过拟合试验数据法,对RLAS悬架刚度特性与RLAS载荷和工作高度之间的关系进行了研究。但RLAS的刚度特性较难在设计阶段进行准确预测。
胡德安等[7]通过建立RLAS的简化模型对不同活塞外锥角下RLAS的刚度特性进行了分析,结果表明,在一定范围内RLAS刚度随活塞外锥角角度增大而提高。Li等[8-9]也推导了列车用的RLAS的有效面积及变化率的计算公式,给出了RLAS的垂直刚度公式。唐传茵等[10]进一步采用有限元法建立了直线型活塞轮廓的RLAS结构参数模型,分析有效面积变化率对刚度特性的影响规律。赵亚敏等[11]在考虑气囊外径变化的情况下,针对直线型活塞轮廓的RLAS刚度模型进了了进一步优化,理论与实际刚度误差控制在10%以内。李静等[12]考虑活塞圆弧过渡,采用曲面积分按活塞设计形状分段推导RLAS刚度特性模型,分析了活塞主要设计参数对RLAS刚度特性的影响规律。Xu[13]通过对铁路列车用的RLAS活塞进行几何分析,得出有效面积的表达式。
上述研究深化了RLAS结构参数、刚度的理论,对RLAS的工程应用起了重要作用。然而,均忽略了RLAS工作时因高度变化引起气囊内部气压变化对RLAS外径变化的影响,鲜有涉及直线与圆弧复合的复杂活塞轮廓的RLAS非线性结构参数建模,缺乏一般性;且涵盖四个参数的RLAS完整结构参数模型极少报道。
综上所述,目前国内外研究主要以圆柱形或圆锥形活塞(直线型活塞轮廓)的RLAS为主,对直线与圆弧复合的复杂活塞轮廓的RLAS非线性结构参数研究较少,缺乏完整的复杂活塞轮廓的RLAS非线性结构参数统一模型。而商用车车身、座椅空气弹簧广泛采用曲线型活塞轮廓的RLAS,以满足乘坐舒适性及安全性等要求。但曲线等复杂活塞轮廓设计使结构参数非线性变化,参数化设计及结构参数预测难度大,因而建立复杂活塞轮廓的RLAS非线性结构参数统一模型可为活塞精细化设计与RLAS力学特性设计、优化提供理论依据。
1 RLAS非线性结构参数统一模型
空气弹簧的刚度为
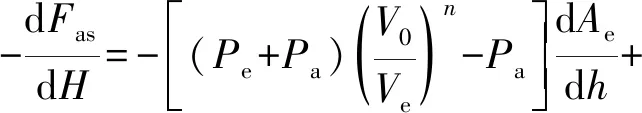
(1)
式中:Fas为某高度时的空气弹簧承载力;Ve为某高度时的有效体积;Ae为某高度时的有效面积;Pe为RLAS气囊内的相对气压;V0为静平衡时的有效体积;Pa为大气压强;H为空气弹簧总成高度,且H=H0+h,H0为静平衡高度,h为RLAS高度变化量;n为多变指数。
由式(1)可知,有效面积及其变化率、有效体积及其变化率是决定RLAS刚度的关键参数,文中将复杂活塞轮廓分段处理,结合几何及力学分析得出各分段的结构参数模型。复杂活塞轮廓的RLAS结构设计模型,如图1所示。

图1 复杂活塞轮廓RLAS结构设计模型
图1中:Ha为活塞作用高度;Ht、H2为气囊与活塞接触相切所产生的高度变化参量;H3~H7为活塞设计参数;H8为气囊上卷曲面到上盖台阶面高度;R0为气囊外表面半径;R1为上压环扣压后的外半径;Ra为活塞顶端半径;Rb为活塞底端半径;K1、K2分别为活塞轮廓坐标系原点到活塞轮廓上侧面、下侧面的距离;Re为气囊的有效半径;Rt为气囊下卷曲位置的半径;Rs为气囊上卷曲位置的半径;Rw为圆弧段圆弧的半径;Ru为过渡段圆弧的半径;α为气囊与活塞形成的内锥角;假设Rs=Rt,气囊内经线长度S保持不变。
当活塞运动时,气囊有效半径、气囊下卷曲位置半径、气囊上卷曲位置半径、气囊与活塞形成的内锥角、空气弹簧有效面积、空气弹簧有效体积等参数将会随气囊所接触的活塞外轮廓段不同而形成分段函数。故在后文中Red~ReIV分别表示为第〇段~第IV段曲线对应的有效半径;Rt0~RtIV分别表示为第〇段~第IV段曲线对应的下卷曲位置的半径;Rs0~RsIV分别为第〇段~第IV段曲线对应的上卷曲位置的半径;α0~αIV分别表示为第〇段~第IV段曲线对应的气囊与活塞形成的内锥角;Ae0~AeIV分别表示为第〇段~第IV段曲线对应的有效面积;Ve0~VeIV分别表示为第〇段~第IV段曲线对应的有效体积。
复杂活塞轮廓形状由直线和圆弧组合,如图2所示。其他活塞轮廓可在此轮廓上简化得到,即文中研究的直线和圆弧复合的复杂活塞轮廓具有一般性。根据曲线型活塞轮廓的设计形状,将其分为导入段(〇段)、活塞段(Ι~V段)及活塞终止段VI段。其中,活塞工作段为Ι~III段,活塞保护段为IV~V段。由于工作时橡胶气囊主要沿活塞工作段滚动,部分气囊壁在极限行程时会接触活塞外壁上的气囊保护段,且限于篇幅原因,本文主要对直线和圆弧复合的Ι~ΙV段进行叙述。
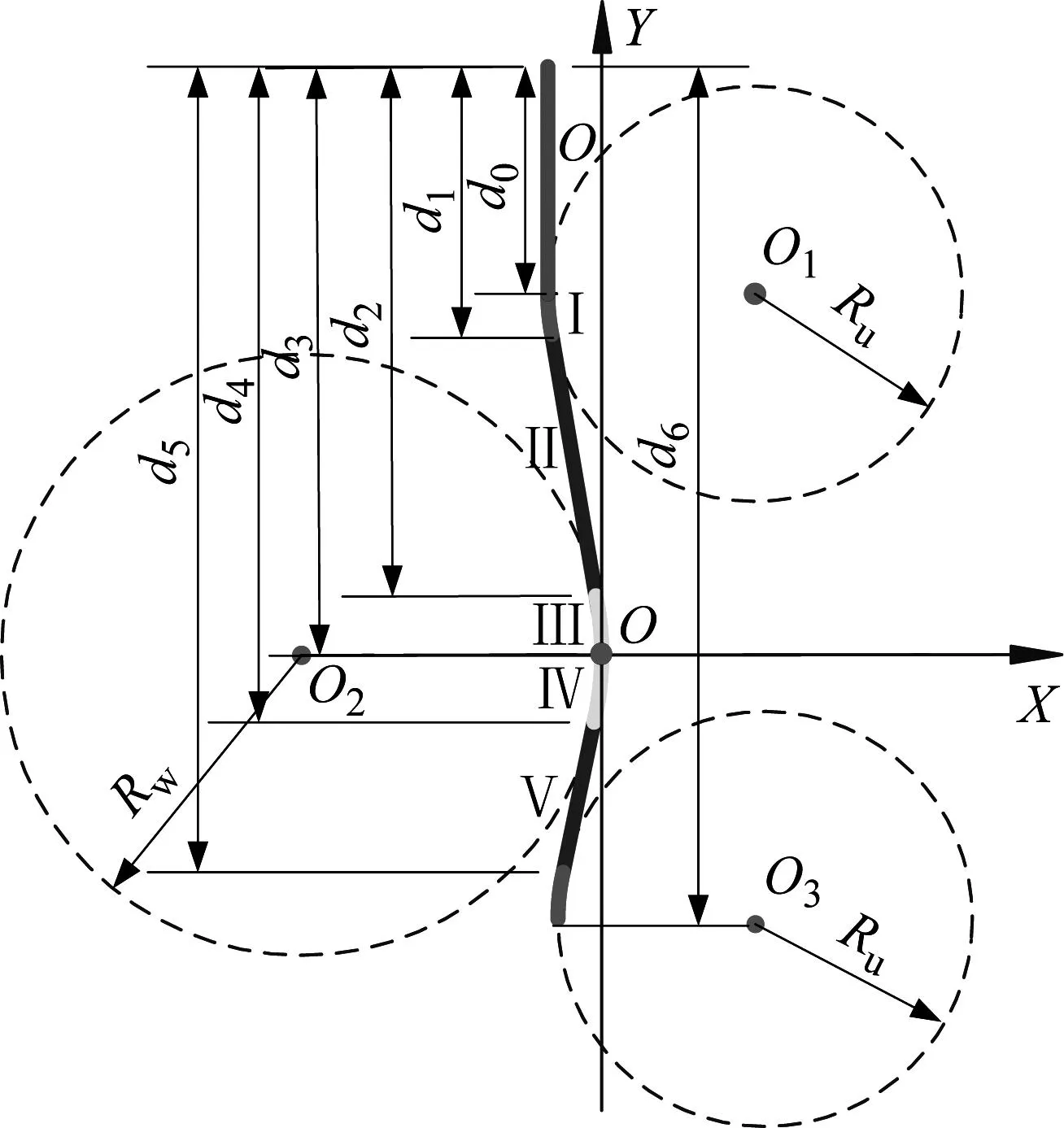
图2 复杂活塞轮廓坐标系
以活塞轮廓直径最小处O点为原点建立坐标系,气囊与活塞接触点为U(x,y)(见图1),得到复合曲线型轮廓的函数方程式如下
(2)
1.1 有效面积及有效面积变化率数学模型
1.1.1 第〇段
当RLAS橡胶气囊运动到图2第〇段曲线(导入段)位置时,即气囊接触点从M点运动到N点位置时,如图3所示。由图3几何关系可得
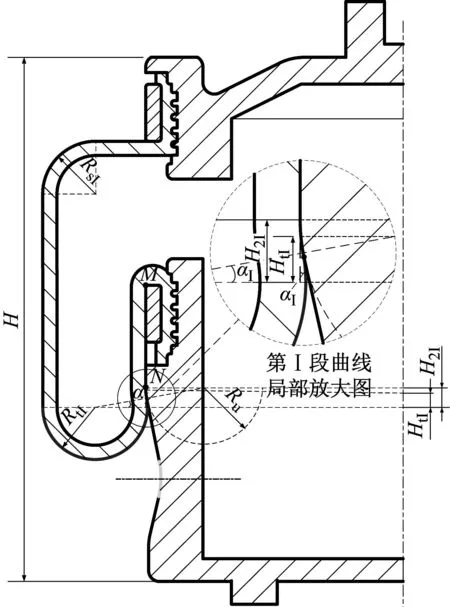
图3 气囊卷曲与过渡段I曲线接触图
Rt0+Re0=R0
(3)
Rt0=Re0-Ra
(4)
联立式(3)、式(4)得有效半径为
Re0=(R0+Ra)/2
(5)
因此,有效面积为
(6)
将Ae0对RLAS的高度变化量h求导,得出有效面积的变化率为
dAe0/dh=2πRe0×dRe0/dh
(7)
式中,dRe0/dh由式(5)求导可得。
1.1.2 第I段曲线
当RLAS橡胶气囊运动到第I段曲线(过渡段)位置时(见图3)。此时该段曲线的函数方程式为
(8)
HtI、H2I为气囊与活塞接触相切所产生的高度变化参量(见图3),由图3几何关系,得到:
RtI+ReI=R0
(9)
(10)
ReI=Ra+RtI×secαI-HtI×tanαI
(11)
联立式(9)、式(11)得
(12)
联立式(10)、式(12)得
HtI=[Ru(sinαI-tan(αI/2))+(R0-Ra)×
tan(αI/2)cosαI]/(1-sinαItan(αI/2))
(13)
则有效半径为
(14)
因此,有效面积为
(15)
式中,AeI为第I段曲线对应的有效面积,其中
αI=arctan[(b1-y)/(a1-x)]
(16)
将AeI对h求导,得出有效面积的变化率为
dAeI/dh=2πReI×dReI/dh
(17)
其中

(18)
式中,dHtI/dh由式(13)求导可得。
1.1.3 第II段直线段
当橡胶气囊运动到第II段曲线(直线段)位置时,如图4所示。此时该段曲线的函数方程式为

图4 气囊卷曲与直线段II曲线接触图
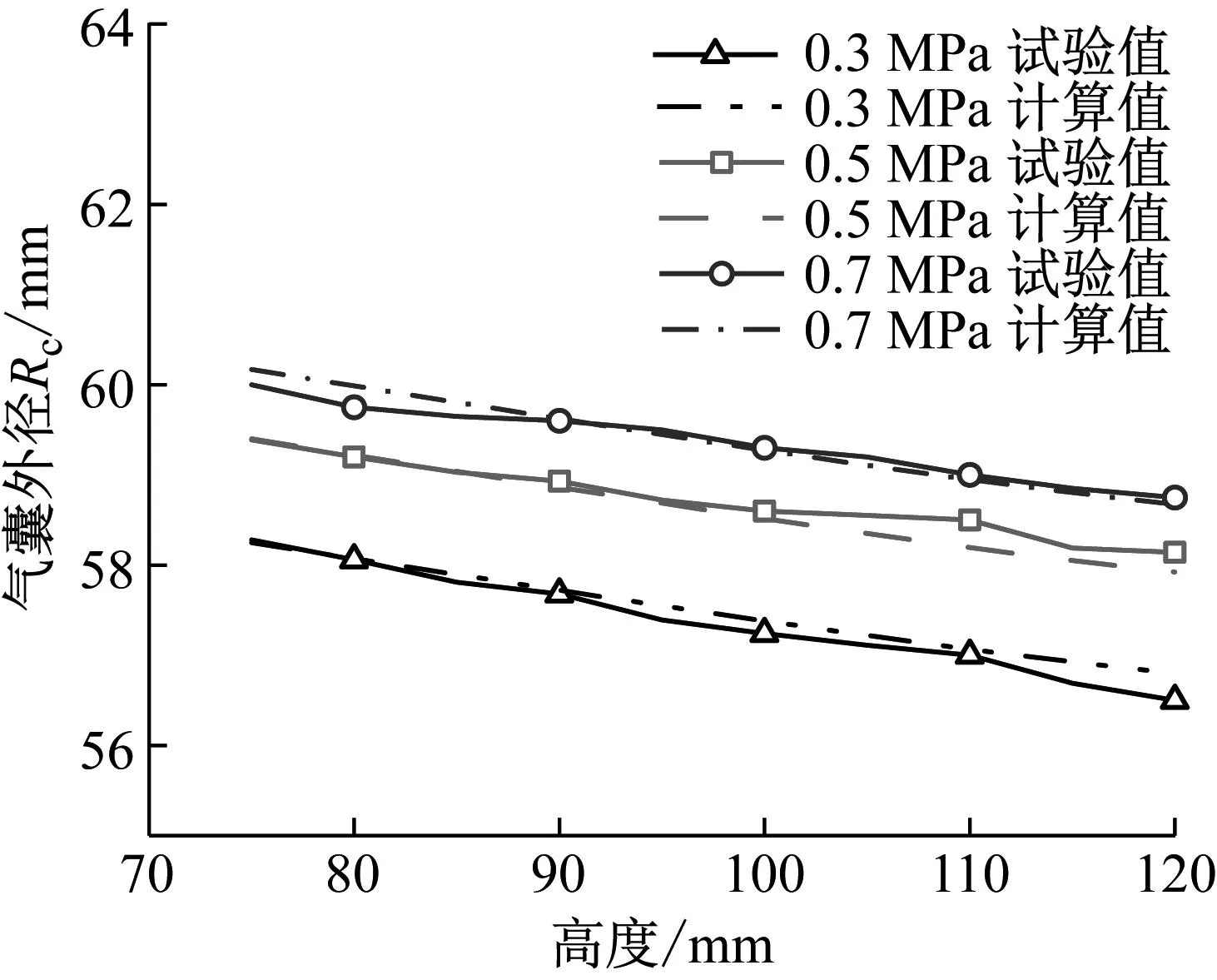
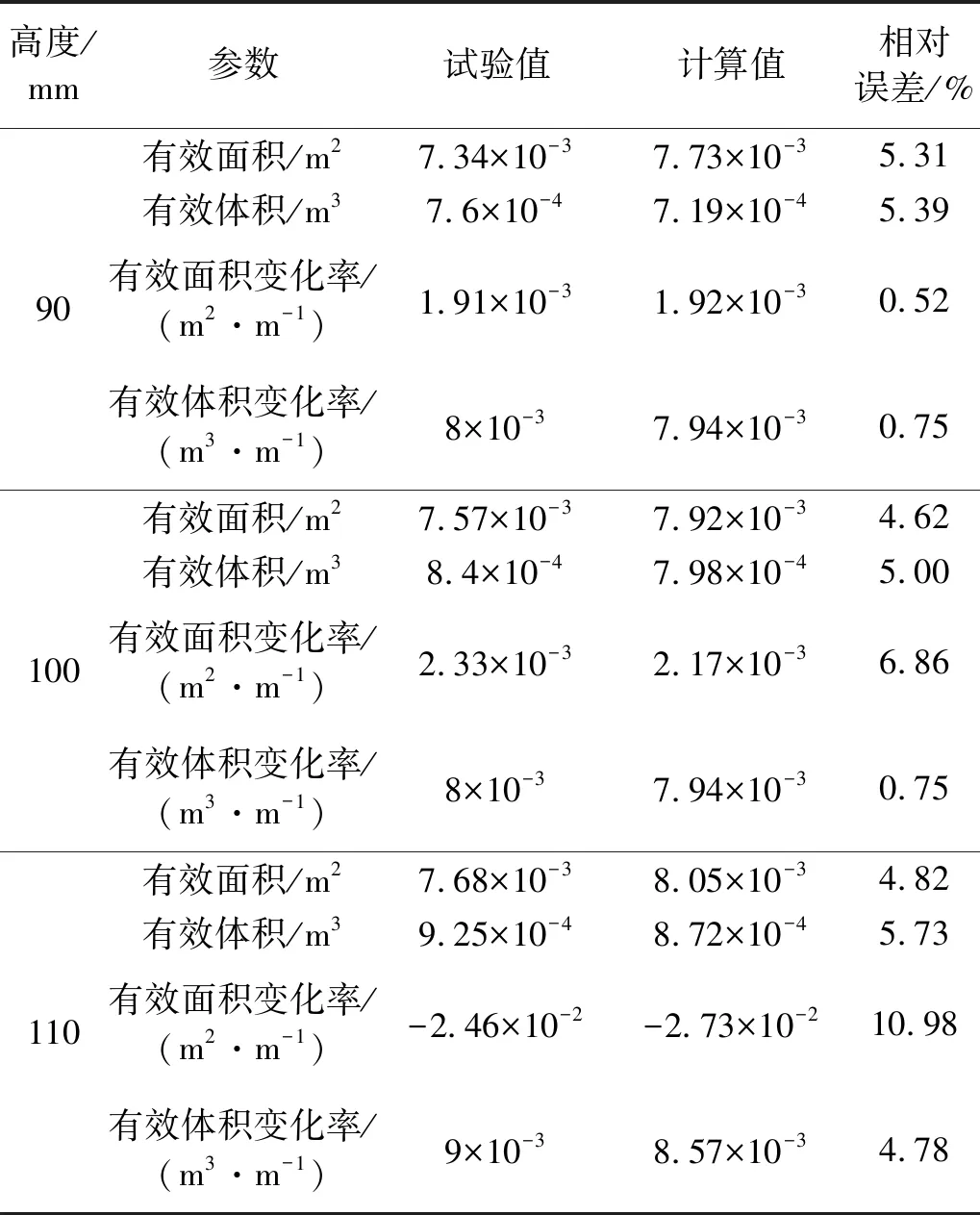
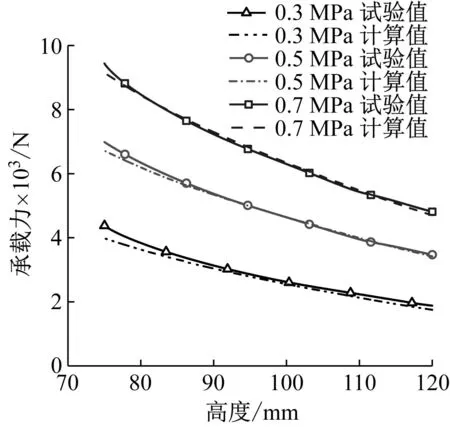
-a2x+b2=y,d1 (19) 由图4几何关系,可得各段弧长为 (20) 联立式(20)可得 (21) (22) (23) 因此, (24) 将HtII对h求导,得: (25) 由图4几何关系,根据式(9)、(11)、(12)、(14)可以得到有效面积为 (26) 式中 αII=arctan(1/a2) (27) 将AeII对h求导,得出有效面积的变化率为 (28) 1.1.4 第III段上圆弧 当RLAS橡胶气囊运动到第III段曲线(上圆弧段)位置时,如图5所示。此时该段曲线的函数方程式为 图5 气囊卷曲与上圆弧段III曲线接触图 (29) 由图5几何关系,得到: ReIII=Ra+RtIIIcosαIII-(K1+x) (30) 联立式(3)、式(30)得 (31) 因此,有效面积为 AeIII=πReIII (32) 式中 αIII=arctan[(y-b3)/(x-a3)] (33) 将AeIII对h求导,得出有效面积的变化率为 (34) 式中 (35) (36) (37) 式中,dαIII/dh由式(33)求导可得。 1.1.5 第IV段下圆弧 当RLAS橡胶气囊运动到第IV段曲线(下圆弧段)位置时,如图6所示。此时该段曲线的函数方程式为 图6 气囊卷曲与下圆弧段IV曲线接触图 (38) 由图6几何关系,得到: ReIV=Rb+RtIVcosαIV-(K2+x) (39) 联立式(3)、式(39)得 RtIV=[R0-Rb+(K2+x)]/(cosαIV+1) (40) 因此,有效面积为 (41) 式中 αIV=arctan[(y-b4)/(a4-x)] (42) 将AeIV对h求导,得出有效面积的变化率为 dAeIV/dh=2πReIV×dReIV/dh (43) 式中 (44) (45) 式中,dαIV/dh由式(42)求导可得。 1.2.1 第〇段 当RLAS橡胶气囊运动到第〇段曲线(导入段)位置时,如图7所示。此时体积公式为 图7 导入段〇体积示意图 Ve0=V1+V2+V3+V4+V5O+V6+V7O (46) 式中 (47) (48) (49) (50) (51) (52) (53) 式中:R2、R6~R8、H11、H13~H17为活塞设计参数;R3~R5、H9~H10、H12为上盖设计参数。 将Ve0对h求导,得出有效面积的变化率为 (54) 1.2.2 第I段曲线 当RLAS橡胶气囊运动到第I段曲线(过渡段)位置时,如图8所示。此时体积公式为 图8 过渡段I体积图 VeI=V1+V2+V3+V4+V5+V6+V7I+V8I+V9I (55) 式中 (56) (57) (58) (59) 将Ve1对h求导,得出有效面积的变化率为 (60) 1.2.3 第II段直线段 当RLAS橡胶气囊运动到第II段曲线(过渡段)位置时,如图9所示。此时体积公式为 图9 直线段II体积图 VeII=V1+V2+V3+V4+V5+V6+V7+V8II+ (61) 式中 (62) (63) (64) (65) 将VeII对h求导,得出有效面积的变化率为 (66) 1.2.4 第III段上圆弧 当RLAS橡胶气囊运动到第III段曲线(上圆弧段)位置时,如图10所示。此时体积公式为 图10 上圆弧段III体积图 VeIII=V1+V2+V3+V4+V5+V6+V7+V8+V9III+V10III+V11III (67) 式中: (68) (69) (70) (71) 将VeIII对h求导,得出有效面积的变化率为 (72) 1.2.5 第IV段下圆弧 当RLAS橡胶气囊运动到第IV段曲线(下圆弧段)位置时,如图11所示。此时体积公式为 图11 下圆弧段IV体积图 VeIV=V1+V2+V3+V4+V5+V6+V7+V8+V9+ (73) 式中 (74) (75) (76) 将VeIV对h求导,得出有效面积的变化率为 (77) 综上所述,RLAS分段非线性结构参数统一模型如下 有效面积公式为 (78) 有效面积变化率为 (79) 有效体积公式为 (80) 有效体积变化率为 (81) 根据式(1),RLAS处于静平衡高度H0的刚度为[14-15] (82) 式中:Pe0为静平衡高度时RLAS内部相对气压;A0、V0分别为静平衡高度时的RLAS的有效面积、有效体积。RLAS承载力为[16] Fas=PeAe (83) 采用本课题组与国内某企业联合设计、制造的RLAS样品A作为试验对象,试验装置如图12所示。主要由MTS852.05(含力传感器和位移传感器)、精密调压阀(型号SNS IR2020-02)、开关阀及气源等组成。 图12 RLAS结构参数测试装置 试验时,在静平衡位置向RLAS内部充入相对气压分别为3×105Pa、5×105Pa、7×105Pa后关闭开关阀,试验速度为10 mm/min,将气囊调节至110 mm高度,气囊从110 mm高度开始,高度每(增加)减少5 mm,测量该时刻的气囊最大外径,同时记录该高度下的承载力值,在总成高度75~120 mm范围下通过试验得到不同气压下的气囊外径-总成高度曲线和承载力-总成高度曲线。 其次,试验时分别保持RLAS内部相对气压恒定为3×105Pa、5×105Pa、7×105Pa,试验速度为10 mm/min的三角波,在总成高度75~120 mm范围下通过试验得到不同恒定气压下的承载力-总成高度数据。将承载力-总成高度数据除以相对恒定气压并求导可分别得到不同高度下的有效面积、有效面积变化率。 最后,用水填充RLAS,将气囊高度调节至120 mm,保证内部相对压强恒定为0.5 Mpa,试验速度为10 mm/min。气囊从最大拉伸高度120 mm开始,高度每减少10 mm,读出排出水量并记录,直至气囊高度降低到75 mm,试验得到有效体积-总成高度曲线,求导可得有效体积变化率-总成高度曲线 。样品A活塞轮廓坐标参数和设计参数,如表1、表2所示。 表1 样品A活塞轮廓坐标参数 表2 样品A设计参数 复杂轮廓的RLAS工作时高度变化使其内部相对压强变化,气囊外径亦相应变化。故对气囊外径进行拟合得到在静平衡位置时不同初始气压下气囊膨胀外径R0与总成高度的函数关系,如下: R0=E×[(A×H2+B×H+C)×Pe0]D (82) 式中,A、B、C、D、E为拟合系数。其中A=0.02,B=-5.8,C=500,D=0.383,E=45.8。不同气压下样品A气囊外径变化,如图13所示。由图13可知,不同气压下R0试验值与计算值最大相对误差为0.54%,表明气囊膨胀外径拟合式(84)的正确性和有效性。 图13 不同气压下样品A气囊外径变化对比图 0.5 MPa下有效面积、有效体积对比,如图14所示。从图14中得到有效面积、有效体积计算值与试验值的最大相对误差分别为5.31%和5.73%,吻合度较好。不同高度时样品A结构参数,如表3所示。表3给出的样品A四个结构参数最大相对误差为10.98%,表明了文中建立的复杂轮廓RLAS非线性结构参数统一模型的正确性[17-18]。 表3 不同高度时样品A结构参数值 图14 0.5 MPa下有效面积、有效体积对比图 不同压强下试验力与计算力对比,如图15所示。由图15可知,采用文中提出的结构参数统一模型辨识得到的四个结构参数计算不同压强下RLAS承载力曲线与试验曲线吻合度很好,承载力相对误差小于9%。静平衡位置时不同压强下样品A刚度值,如表4所示。表4给出不同压强下样品A刚度最大相对误差为6.99%,进一步验证了RLAS结构参数统一模型的有效性。 表4 静平衡位置时不同压强下样品A刚度值 图15 不同压强下试验力与计算力对比图 复杂活塞轮廓的关键设计参量包括圆弧段半径、直线段内锥角。为减少RLAS活塞上的应力集中,保证活塞轮廓复合曲线设计连续性,改变活塞直线段的内锥角时,应相应改变复合曲线的圆弧半径,以提高活塞轮廓形状的连续性和光滑性,提升RLAS疲劳寿命[19]。 选取气囊相对内压为5×105Pa下,分析关键设计参量分别对导入段〇段(108~120 mm)、I段(105~108 mm)、直线段II段(86~105 mm)、圆弧段III-IV段 (75~86 mm)结构参数及力学特性的影响。圆弧半径或内锥角在不同阶段对有效面积的影响,如图16所示。由图16可知,当圆弧段的圆弧半径增大8.2 mm时,有效面积增加了173 mm2,有效面积随着圆弧半径的变化上下移动,形成平移特性。同时,固定圆弧半径下的圆弧段有效面积曲线随高度变化呈现先减小后增大趋势,但总体上趋于平缓。直线段有效面积与内锥角成反比特性,某一内锥角度下有效面积与高度呈正比和线性关系。当活塞内锥角改变8°时,直线段区间内的有效面积最大变化了285 mm2。 图16 圆弧半径或内锥角在不同阶段对有效面积的影响 圆弧半径或内锥角在不同阶段对有效面积变化率影响,如图17所示。由图17可知,活塞内锥角对有效面积变化率的影响随角度的增加而平移增加,且在直线段II的有效面积变化率基本恒定。当活塞内锥角趋于0°时,此时直线段有效面积变化率趋于零(其曲线与横坐标重合);当活塞内锥角趋于90°时,此时直线段有效面积变化率趋于无穷大(其曲线与横坐标平行且趋向无穷远处);即活塞内锥角由0°逐渐变为90°时,直线段的有效面积变化率曲线在第一象限内呈现出上下平移效应。 图17 圆弧半径或内锥角在不同阶段对有效面积变化率影响 当圆弧半径趋于无穷小时,圆弧段的形状趋于横向直线,此时有效面积变化率曲线趋于与纵坐标平行;当圆弧半径趋于无穷大时,圆弧段的形状趋于垂向直线,此时有效面积变化率趋于某一恒定值(与横坐标共线);即圆弧半径由无穷小逐渐变为无穷大时,圆弧段的有效面积变化率曲线在第一象限内呈现顺时针旋转效应。 在内锥角趋于0°前提下,若圆弧半径趋于无穷大,活塞轮廓由复合曲线型演变为直线轮廓(圆柱型活塞);若圆弧半径为某一定值,活塞轮廓为纯圆弧型(束腰型活塞)。在内锥角为某一定值时,若去掉圆弧段(或圆弧半径趋于无穷小)及保护段,活塞轮廓亦演变为直线型轮廓(圆锥型活塞)。即其他活塞轮廓均可在复杂活塞轮廓上简化得到,亦表明文中研究的复杂活塞轮廓具有一般性。 RLAS在工作过程中圆弧半径和直线段内锥角对有效体积的影响,如图18所示。从图18可知, RLAS有效体积随关键设计参量的变化可忽略不计。 图18 圆弧半径或内锥角在不同阶段对有效体积的影响 圆弧半径或内锥角在不同阶段对有效体积变化率影响,如图19所示。由图19可知,圆弧段有效体积变化率与圆弧半径大小成正比,与RLAS高度成反比,且随着圆弧半径的增大,对有效体积变化率的影响减小。直线段内,当RLAS高度在86~90 mm之间时,有效体积变化率与活塞内锥角大小成反比。而当RLAS高度大于90 mm时,随着活塞内锥角的增大,直线段内有效体积变化率的波动略大,主要源于内锥角的增大导致有效体积增长,从而导致有效体积变化率的波动略大。但因有效体积变化很小,有效体积变化率最大仅变化了0.08%,总体而言影响不够显著。 圆弧半径或内锥角在不同阶段对承载力的影响,如图20所示。图20给出了不同高度下圆弧半径和直线段内锥角对承载力的影响,RLAS承载力与内锥角成反比特性、与圆弧半径成正比特性,但整体受关键设计参量变化的影响很小。 图20 圆弧半径或内锥角在不同阶段对承载力的影响 圆弧半径或内锥角在不同阶段对刚度的影响,如图21所示。从图21可知,除过渡段外,RLAS刚度随高度的下降整体呈上升趋势,且在过渡段和直线段内,刚度与内锥角成反比特性。在圆弧段内,圆弧半径越大,圆弧段刚度的变化越平缓。 图21 圆弧半径或内锥角在不同阶段对刚度的影响 综上所述,增大直线段(II)内锥角且减小圆弧段(III、IV)圆弧半径可降低有效面积、增大有效面积变化率,有效降低活塞工作段(I-III)的刚度,同时提升下圆弧段的刚度(IV),而对承载力和有效体积及其变化率影响很小。因此,复杂活塞轮廓的RLAS设计有利于平衡活塞工作段内低刚度与下圆弧段高刚度的矛盾需求,RLAS非线性结构参数统一模型为RLAS活塞由单一直线或曲线轮廓迈向复合曲线轮廓精细化设计、优化提供理论指导。 文中建立了直线与圆弧复合的复杂活塞轮廓RLAS非线性结构参数统一模型,验证了结构参数统一模型的有效性、一般性。 进一步揭示了内锥角、圆弧半径两个关键设计参量对结构参数的影响规律,指出内锥角、圆弧半径与有效面积分别成反比、正比特性,与有效面积变化率分别呈平移效应和旋转效应;内锥角、圆弧半径对有效体积及其变化率和承载力影响较小,可以忽略。内锥角与刚度成反比特性,大内锥角与小圆弧半径使RLAS活塞工作段(I~III)刚度低,而下圆弧段刚度(IV)高,实现了工作段低刚度需求与下圆弧段安全保护性提升的协同设计。 研究结果为RLAS结构参数设计与优化、刚度及承载特性准确预测提供了重要的理论支撑。



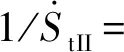




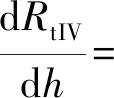
1.2 有效体积及有效体积变化率数学模型







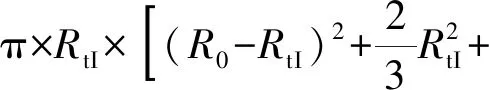

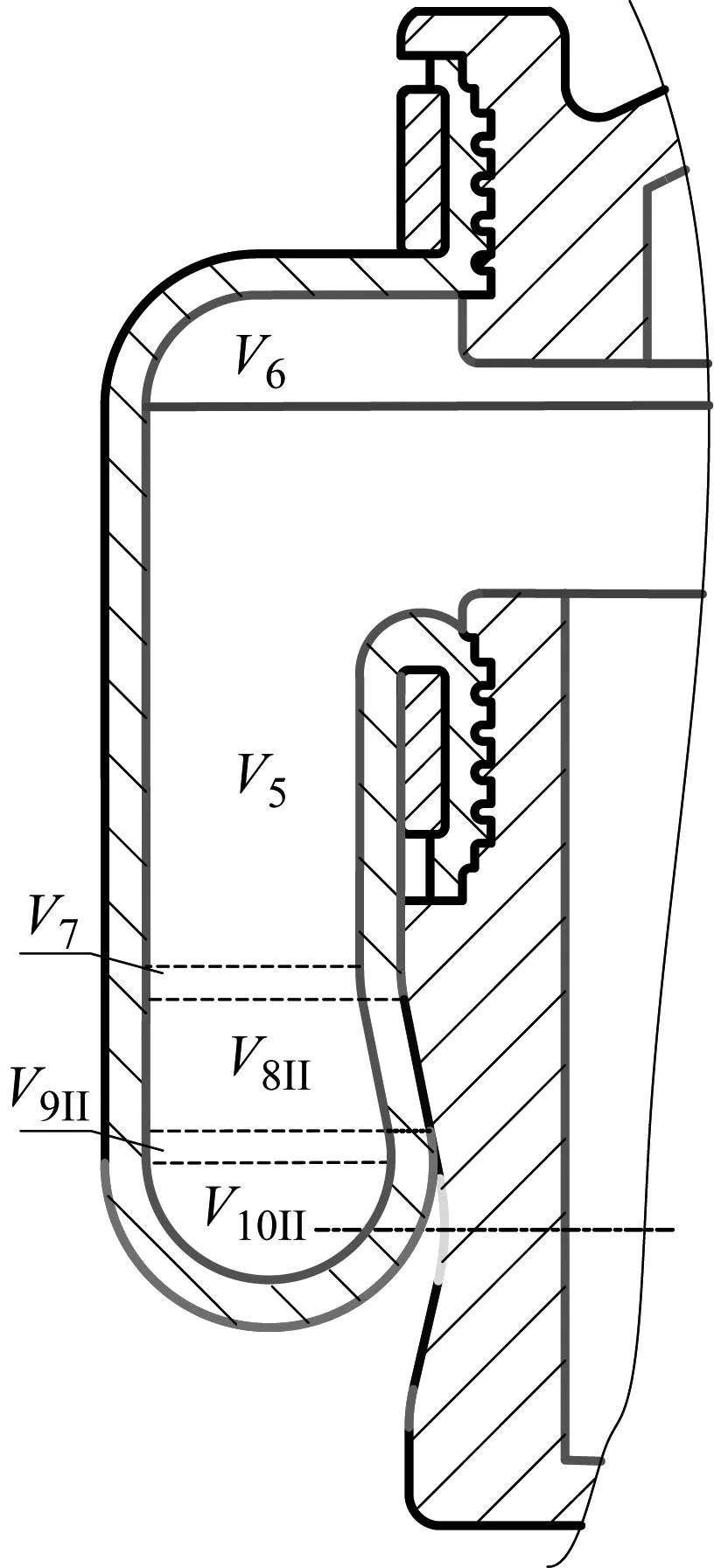
V9II+V10II
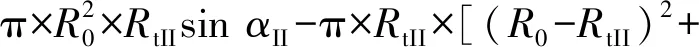


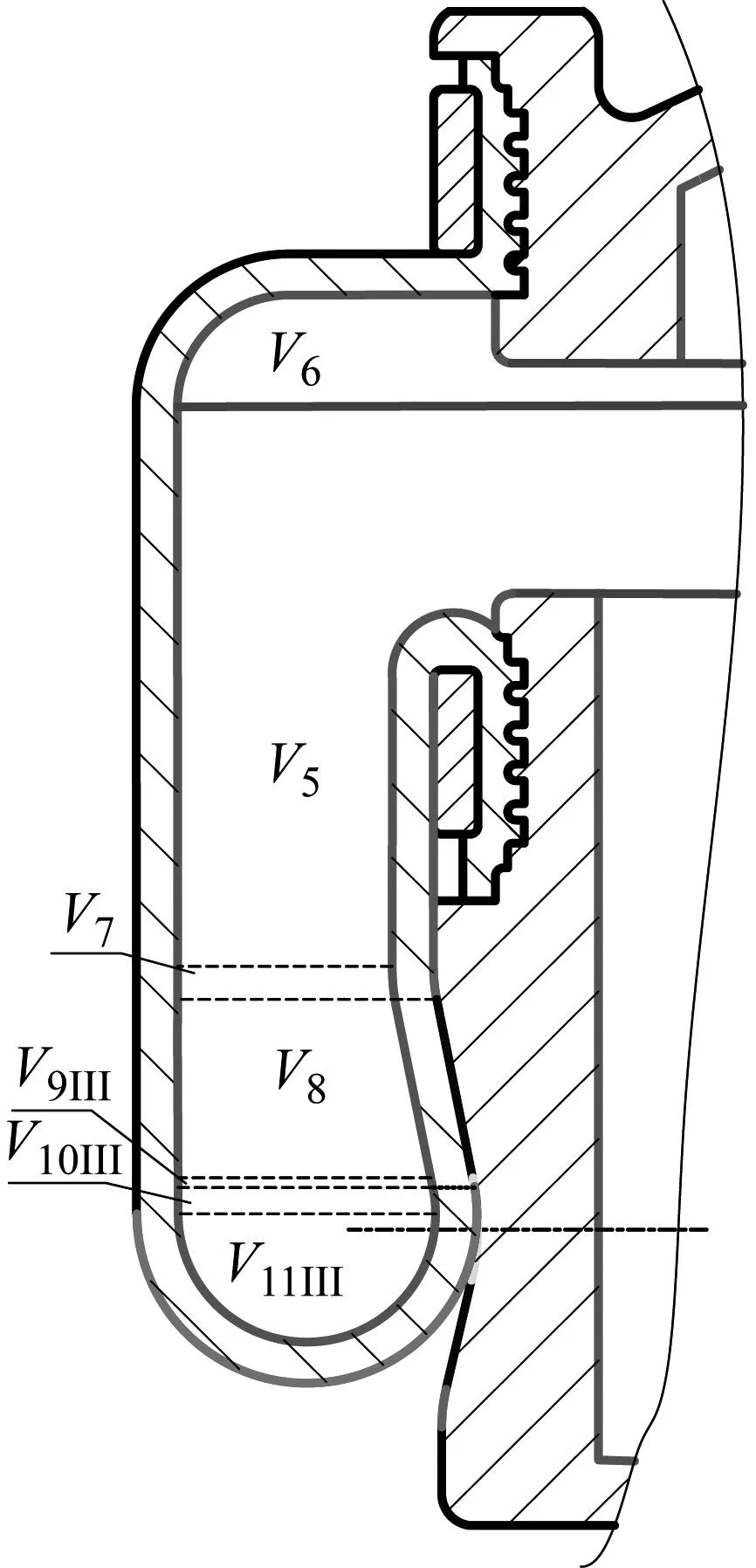
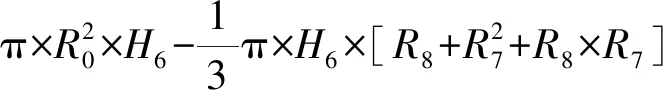


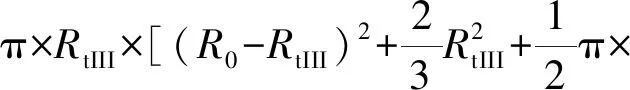
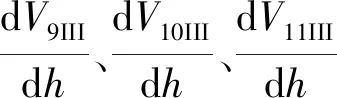
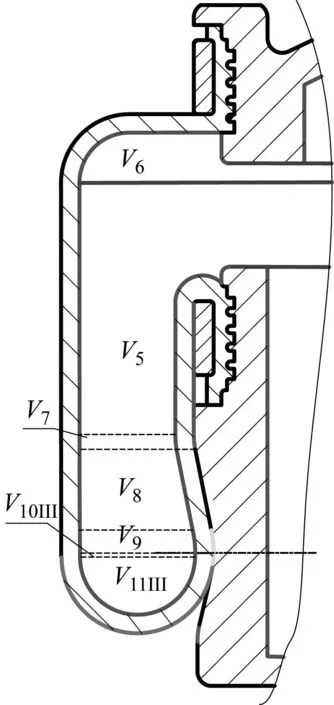
V10IV+V11IV



1.3 非线性结构参数统一模型

2 试验验证
2.1 试验装置及试验方法



2.2 试验验证


3 关键设计参量灵敏度分析





4 结 论
