楔形船艏舷侧撞击场景下甲板结构损伤预报解析方法研究

周家有, 赵延杰, 张伦平, 张一弛, 袁昱超, 唐文勇

(1.上海交通大学 海洋工程国家重点实验室,上海 200240;2.上海交通大学 船舶海洋与建筑工程学院,上海 200240;3.中国船舶科学研究中心,江苏 无锡 214082;4.深海技术科学太湖实验室,江苏 无锡 214082)

随着全球航运业的不断发展,海上航线愈发稠密,船舶碰撞事故时有发生。船舶碰撞是在短时间内产生巨大冲击载荷作用的一种复杂非线性动态响应过程,常造成船舶结构撕裂,继而引发货品泄露,造成重大经济损失、环境污染以及人员伤亡等。尽管各种先进设备与技术被用于提高船舶航行安全性,但船舶结构本身的抗撞性评估仍具有重要的工程意义。

目前船舶碰撞的研究方法有模型试验法、非线性有限元分析法,经验公式法以及简化解析法。其中,简化解析法以其快速性与准确性特点在工程实践领域广受欢迎。该方法旨在通过对真实碰撞场景中各构件损伤变形模式的观察,分别建立各构件变形损伤的简化数学模型,而后根据塑性力学理论推导解析公式,得到构件变形的结构抗力和能量耗散,Zhang[1]推导了一系列著名的解析公式,对矩形板材在面外载荷下发生塑性变形、桁材等构件在面内载荷下的压溃与破碎、十字结构的压溃变形、光板撕裂变形场景下产生的结构抗力以及能量耗散进行评估;Haris等[2]考虑撞击船艏与被撞舷侧变形的相互影响,使用简化解析方法对船艏及舷侧被撞区域的结构损伤进行预报;Gao等[3]基于一系列简化解析公式提出了新的分析方法用于快速预报FPSO舷侧结构在正撞场景下的响应;其他解析模型也可参考文献[4-11]。通过文献调研发现,解析方法的建立常基于部分假设。如各构件及各变形模式相互独立,而后,通过对各构件计算结果叠加而得到整体结构的响应。该假设忽略了构件间存在的耦合作用,在部分复杂场景计算中或可造成误差。因此,在未来解析方法发展中,更需从机理层面考虑各构件的耦合效应,使整体解析预报方法适用性更广,结果更加准确。其次,目前解析方法对整体结构预报中,重点考量了单个构件的单一变形模式。但在实际碰撞过程,由于撞深、碰撞角度等复杂因素的变化,单类构件可能存在多模式变形及损伤演化,对此相关方面研究还不够完善。另一方面,目前船舶碰撞中各构件损伤解析预报方法主要集中于正撞场景。而频率更高的斜撞场景下预报方法依然较少。Wang等[12]、王泽平等[13]研究了斜撞场景下双层壳结构舷侧外板、桁材、肋板的主要变形机理并推导解析公式。但对于海工船、舰船等部分具有单层壳、多级甲板的结构,舷侧撞击场景下结构响应或有不同,如甲板结构遭遇面内冲击载荷,在大撞深下可能发生严重撕裂,对于该类场景的解析预报方法依然有待完善。

因此,本文拟对楔形艏以大撞深、多角度碰撞单层壳舷侧场景下,甲板结构遭遇面内冲击载荷的损伤机理进行研究。通过非线性有限元方法,观察分析结构的动态响应,确定各构件变形损伤模式,根据其结构变形模式将甲板结构划分为四类构件。基于上限定理,考虑多角度碰撞、构件变形的多模式损伤演化、构件之间的耦合变形机理,提出一种预报甲板结构损伤的解析方法,并与数值结果、现有解析公式进行对比验证。研究成果对于大撞深、多角度碰撞场景下甲板结构损伤评估有一定的补充完善,并具有实际工程应用价值。

1 楔形船艏舷侧撞击甲板结构数值仿真

为了探究舷侧碰撞中甲板在各场景下的变形损伤机理,本文首先采用非线性有限元方法,对楔形船艏多角度撞击单层壳船体舷侧结构场景进行分析,确定结构损伤的变形模式,为后续建立解析方法提供基础与验证。

1.1 有限元模型

选取排水量为5 000 t的某海工船作为研究对象,主尺度如表1所示。

表1 被撞船主尺度

船舶碰撞产生的损伤集中在局部区域,考虑到边界条件的影响,建立船舯部两倍横舱壁范围的舱室结构作为被撞区域。模型包含主要的舷侧构件,如舷侧外板、甲板、横舱壁等以及附着于它们之上的加强筋、T型材,如图1所示。

(a)

被撞区域主要材料为船体用结构钢B级,采用双线性弹塑性模型并通过Cowper-Symonds模型考虑应变率影响,材料的失效用极限断裂应变来定义。有关数据:材料密度7 850 kg/m3,杨氏模量2.1×1011N/m2,切线模量1.18×109N/m2,屈服应力2.35×108N/m2,泊松比0.3。最大塑性失效应变取0.20[14]。对于船用钢,Cowper-Symonds本构方程中的两个常数一般取P=5、C=40.4[15]。

为了在保证计算精度的同时具有良好的时效性,有限元模型全局采用130 mm网格,对被撞区舱室采用65 mm网格,总的单元数量为 453 400个。对被撞舱段两端采取固定支撑以限制全局位移,重点关注不同撞深下各构件损伤变形模式。

楔形撞击船艏简化为一个质量为4 500 t的刚性体,如图2所示。撞击速度为2 m/s恒定不变。考虑附连水影响,本文根据经验采用附加质量为0.04倍的船体质量[16]。

图2 撞击船艏

1.2 碰撞场景定义

根据设计吃水,本文选取三个典型的碰撞位置,每个碰撞位置下楔形船艏分别以90°、75°、60°、45°进行撞击,如图3所示。共12种工况,如表2所示。

(a) 撞击位置

表2 碰撞工况

1.3 甲板的损伤变形模式

在所有场景下,甲板1首先发生压溃褶皱变形,范围局限于两个肋骨间距,如图4(a)所示。这一现象随着撞击角度的减小而愈发不明显;甲板与船艏接触边缘存在明显压溃破碎现象,如图4(b)所示。这是由于舷侧外板上加强筋与甲板边缘形成的十字结构发生压溃失效产生的;达到一定撞深后,甲板1发生撕裂变形,裂纹沿撞头方向扩散,两侧板、筋受到挤压向两侧发生卷曲,小角度撞击时可以明显观察到横向加强筋对于光板卷曲的限制作用。

(a) 小范围压溃褶皱

甲板1在各碰撞场景下撕裂后的变形损伤模式相似,如图5所示。但由于楔形撞头撞击位置存在差异,撕裂长度稍有不同,“碰撞位置1”中甲板参与碰撞程度最高、撕裂长度最大。

2 甲板结构损伤解析模型

本章将基于数值方法反馈的结构变形模式,建立甲板结构遭遇面内冲击载荷下的损伤预报解析方法。基本思路为:首先,根据甲板结构特点及各构件变形模式,将甲板结构分为几类承载构件,如图6所示。其中,A类构件用于描述被横舱壁限制的水平光板,其变形模式考虑由压溃褶皱到撕裂变形的损伤演化;B类构件用于描述光板上平行于撞击方向上的横向加强筋,主要发生弯曲变形并与A类构件存在耦合效应;C类构件用于描述光板上垂直于撞击方向上的纵向T型材,变形模式与B类构件相似,但与A类构件不存在耦合效应;D类构件用于描述外板上加强筋与甲板形成的十字结构,主要发生压溃变形。

图6 四类构件

每一类构件遵循不同的塑性变形机理,考虑各构件之间的耦合变形及损伤演化,推导数学解析模型求解各构件在各变形模式下能量耗散,汇总各构件产生的能量耗散,与数值结果进行对比验证,最终形成甲板结构损伤预报解析公式。损伤预报流程如图7所示。

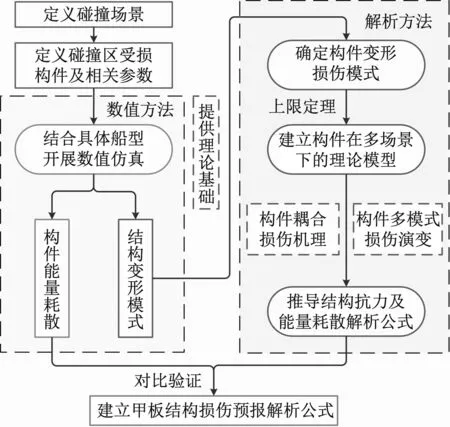
图7 甲板损伤预报流程图

2.1 上限定理

解析方法常用于船舶碰撞中结构响应分析,理论模型的变形模式不仅接近结构真实变形,同时在数学上易于求解。根据上限定理,在碰撞的解析计算中,外力的做功功率等于内部的能量耗散功率,可得:

(1)

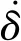
(2)

(3)

式中:t为板的厚度;σ0为材料的流动应力,取屈服应力和极限应力的均值。

2.2 四类构件解析理论模型

2.2.1 A类构件

A类构件用于描述被横舱壁限制的水平光板。在多角度的撞击场景下,A类构件首先发生小范围压溃褶皱变形,针对此类变形,本文参考王泽平等提出的解析模型进行计算,理论模型如图8所示。结构抗力公式如式(4)。

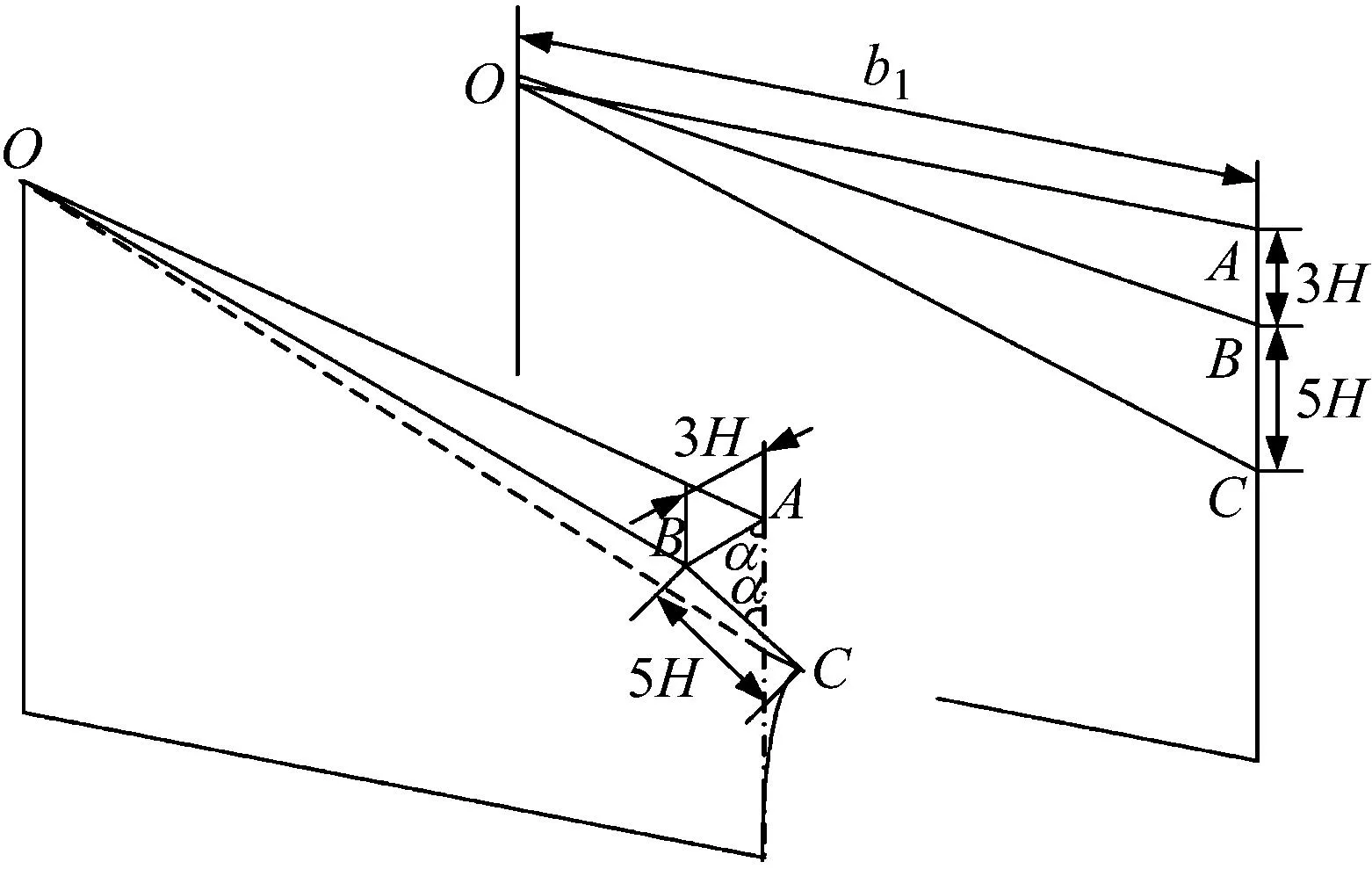
图8 桁材撞击后的理论变形模型

(4)

式中,H=0.165(b2t/sinβ)1/3为褶皱特征高度。

由于船艏倾角的存在,A类构件不存在第二阶段褶皱。当位于船艏前端的光板材料纤维由于船艏的直接推动而张紧,达到临界断裂应变时发生破裂。船艏前端的光板形成裂纹,裂纹随船艏不断向前推进,两侧光板在船艏尖端后卷曲形成两个曲面,如图9所示。假设板在楔形撞头尖端前方的撕裂是由于楔形撞头尖端推动产生的张力引起的,并且不存在裂缝扩展。

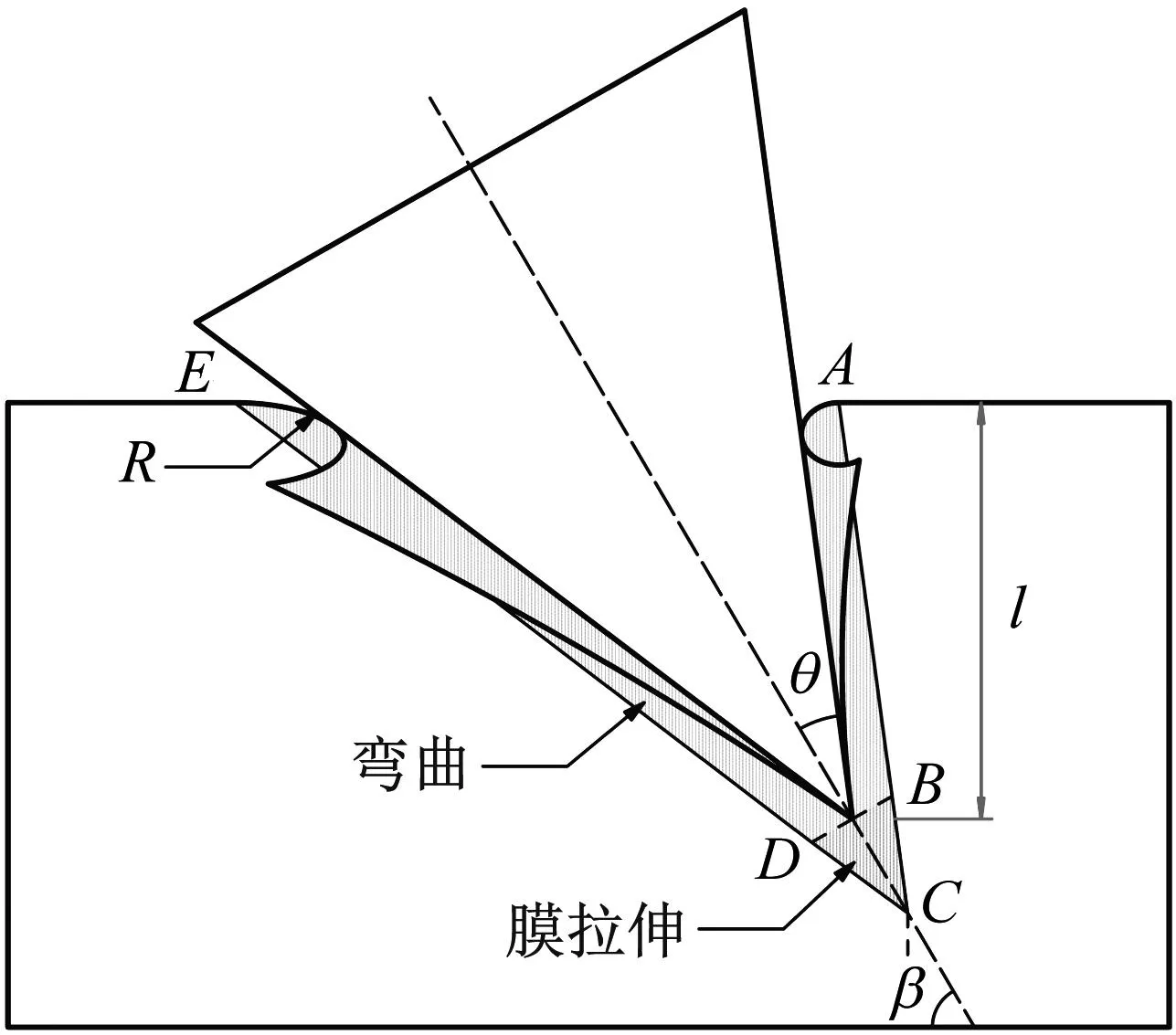
图9 刚性楔块切割板材的分析模型

塑性变形主要发生在ABCDE区域内,该区域之外没有发生塑性变形。塑性变形区域可以通过线BD分割为两部分:第一部分位于楔形撞头尖端前BCD区域内,由于楔形尖端的推动,板在楔形尖端前方的区域会发生薄膜拉伸。随着楔形撞头的前进,BD线上的板发生断裂、分离,在楔形尖端后形成两个圆柱曲面。这两个圆柱形曲面构成了板的第二变形区域,仅承受弯曲变形。

(5)

式中:σ0=(σy+σu)/2为材料的流动应力,取屈服应力和极限应力的平均值;tp为板的厚度;R为待确定的卷曲半径;θ为艏部半角;β为斜撞角度。

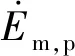
(6)

(7)

式中,b为BD长度的一半。将式(7)代入式(6)

(8)

楔形船艏-甲板结构系统的平衡可通过虚功原理表示为

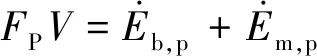
(9)

式中,FP为光板产生的塑性阻力。将式(5),式(8)代入式(9),得出与曲率半径R相关的塑性阻力表达式。考虑到楔形船艏与光板之间的摩擦,板表面上的法向力为Fn=Fp/(2sinθ),使用库仑摩擦定律并将力投射到楔形撞头的方向,得到摩擦阻力为

(10)

式中,μ为摩擦因数。A类构件产生的总阻力可以表示为

(11)

2.2.2 B类构件

B类构件用于描述光板上平行于撞击方向上的横向加强筋。在多角度撞击场景下,A类构件撕裂后于船艏两侧发生卷曲,此过程中B类构件始终垂直于A类构件并发生卷曲。观察碰撞过程中等效塑性应变分布,B类构件对A类构件的卷曲起到限制作用,提高了A类构件卷曲的曲率半径。

在楔形撞头与加强筋接触之前,切割响应几乎相同,但随着碰撞过程的继续,加强筋效应开始显现。B类构件通过与A类构件焊接为一个整体从而提高结构整体的强度和刚度。传统处理B类构件的方法是Paik等[17]提出的等效板厚法,将骨材截面分摊到被依附的板上,通过增加被依附板的厚度来代替骨材的作用。但这一方法不能反应加强筋的变形损伤机理,明显低估了骨材的承载能力。因此,本文提出一种新的考虑骨材的方法。

假设横向加强筋在变形损伤过程中始终与甲板垂直,能量耗散均以弯曲为主。加强筋附着的带板在碰撞过程中展现出明显条纹状等效塑性应变区,其能量耗散不能只按照A类构件进行计算,还应考虑由于加强筋附着而额外产生的这部分能量耗散。具体变形损伤过程如图10所示。

(a)

(12)

式中:ts1为腹板的厚度;ts2为面板的厚度。

2.2.3 C类构件

C类构件用于描述光板上垂直于撞击方向的纵向T型材。C类构件与B类构件变形损伤模式相似,但由于C类构件间距较远,在与船艏直接接触之前对A类构件卷曲无影响,接触后主要以撕裂后供能为主,撕裂前承载不明显。具体变形损伤过程如图11所示。

(a)

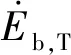
(13)

式中:ht1=h3/sinγ是T型材腹板塑性铰链的长度,面板塑性铰链长度ht2=h4/(2sinγ),带板塑性铰链长度ht3=h5/cos(β-θ);h3,tt1分别为T型材腹板的高度及厚度;h4,tt2分别为面板的宽度及厚度;h5为T型材带板的宽度;γ为楔形船艏的横向倾角。

2.2.4 D类构件

D类构件用于描述外板上加强筋与甲板形成的十字结构,如图12所示。十字交叉构件指的是舷侧外板上横向加强筋与甲板、甲板上横向加强筋交叉形成的结构。当十字构件在交叉轴线处受到轴向压载荷时,初期主要是板的弹性屈曲变形。之后随着撞深加大,板进入塑性变形,十字构件的交叉轴线缩短,并会出现类似板面内受压模型中的褶皱现象。

图12 十字构件变形模型

Wang等[18-19]针对十字构件轴向受压变形提出了不同的阻力计算公式。其中,Yang等提出的解析计算公式计算精度较好且较为简单,故在本章中予以采用。其十字构件受压过程中平均阻力的解析计算公式表达如下

PX=σ0[1.178(2bt2/H)+3.0Ht+1.5t2]

(14)

式中:PX为受压过程中的平均阻力;b和t分别为十字构件各个翼板的宽度和厚度(见图12)。2H为每个褶皱的特征高度,第一个褶皱高度2H的计算表达式为

2H=1.77b1.5/t0.5

(15)

2.3 撕裂变形卷曲半径修正

在求解结构整体能量耗散前,上述四类构件的解析公式中还存在一个未知量,即撕裂变形中甲板结构卷曲的曲率半径。传统求解卷曲半径的方法是通过对A类构件撕裂抗力式(11)求偏导,令∂FP/∂R=0,以此获得最佳卷曲半径,对于B类构件则主要采用等效厚度法计入,两者相互单独考虑求解,忽略构件之间的耦合效应。这种方法求得的卷曲半径较小,这是因为在实际变形过程中由于受到B类构件的限制,A类构件无法像解耦后的理论模型那样完美卷曲,因此单独根据A类构件的响应求解甲板结构整体的卷曲半径是不全面的。本文考虑板筋耦合效应、碰撞角度及板面摩擦的影响,对目前仅考虑正撞场景下解耦得到的甲板结构卷曲半径进行修正,扩大了解析公式的应用范围,从机理层面使结果更加稳定可靠。具体求解方法如下:

首先,考虑A、B类构件总的结构抗力

(16)

式中,m为加强筋参与撞击过程的贡献因子,主要取决于当前撞深下加强筋参与数量及程度。将式(11)、式(12)代入式(16),可以得到

(17)

其中S可以表示为

(18)

其次,基于两类构件总结构抗力表达式,令∂FA+B/∂R=0,可以得到考虑板筋耦合效应下新的最佳卷曲半径R

(19)

新的卷曲半径考虑了各构件的耦合效应,在A类构件的基础上计及B类构件对其的限制作用,同时引入碰撞角度、摩擦因数等参数,扩大了解析公式的适用性。令R=R0l0.5,将式(19)代入式(17)

(20)

A、B类构件的总能量耗散可以表示为

(21)

基于A类、B类构件的结构抗力及能量耗散解析公式,再根据C类、D类构件的参与情况,即可求出甲板结构整体的结构抗力及能量耗散情况。

3 验证与讨论

基于本文推导的理论方法,形成解析计算程序,针对12个工况进行计算,并将得到的能量耗散-撞深曲线与1.3节得到的仿真结果进行对比。可以发现,三者曲线在碰撞过程初期存在拐点,这是由于甲板结构在撞深达到临界值时,会发生损伤演化,甲板的变形损伤模式从压溃褶皱演化为撕裂变形,如图13所示。通过本文解析方法得到的能量耗散曲线很好地捕捉到这一特点。

(a) 初期压溃褶皱

对正撞场景下碰撞位置不同的三个工况进行进一步验证,并同时与等效厚度法的结果进行对比,结果如图14所示。可以明显发现:在小撞深正撞场景下,三者曲线吻合度较高,但随着撞深增大,等效厚度法预报结果更加保守,本文提出的解析方法精度更高。

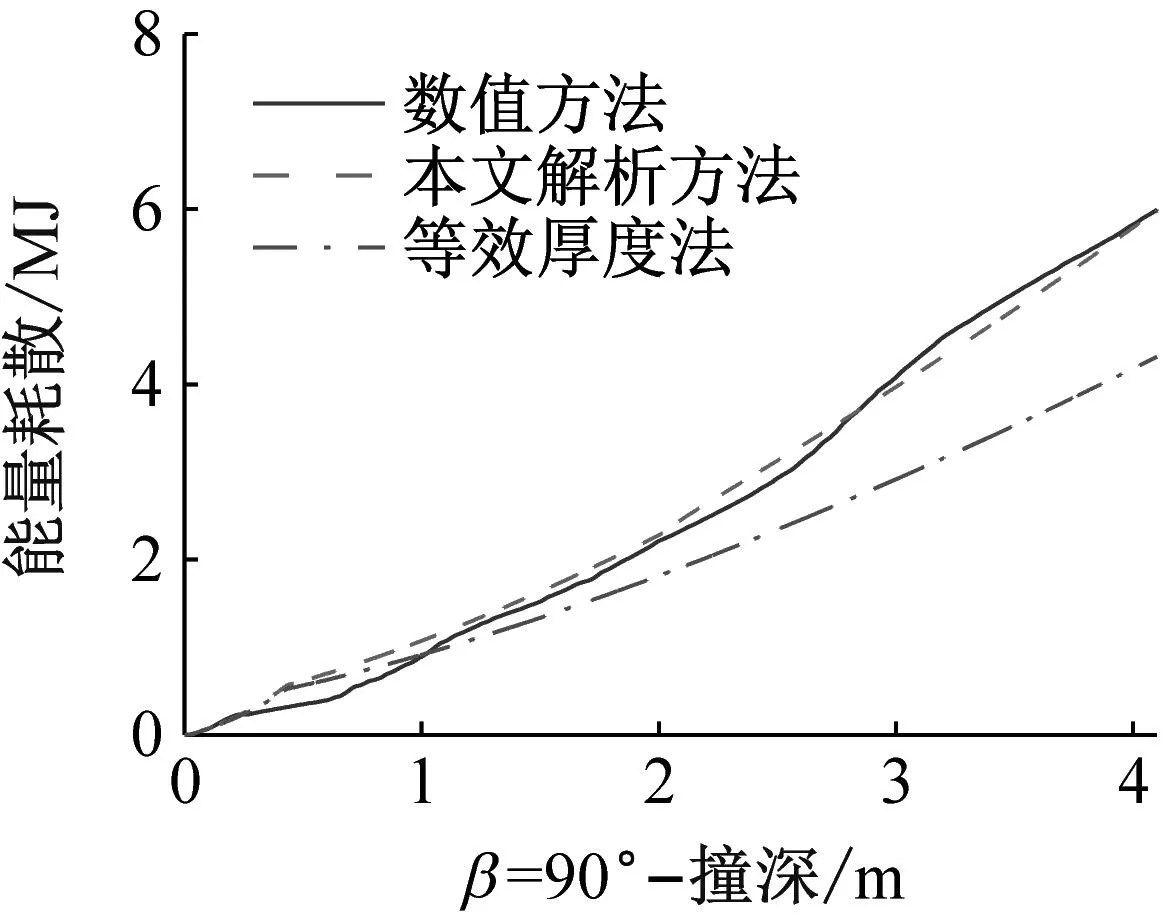
(a) 工况1

对斜撞场景统一选取构件参与度最高的碰撞位置1进行验证,并与等效厚度法的结果进行对比,结果如图15所示。可以同样发现:在斜撞场景下,三种工况初期吻合度良好,但随着撞深增加,尤其是接触到C类构件之后,等效厚度法精度快速下降,而本文方法仍具有较高精度。这是由于等效板厚法是将A类构件上所有B、C类构件在碰撞开始前就全部计入考虑,因此在小撞深场景下虽然等效板厚法低估B类构件的承载能力但又过早的引入C类构件参与,间接起到弥补预报精度的作用。在大撞深场景下、船艏实际接触到C类构件之后,等效板厚法的预报精度快速下降。本文新提出的解析方法对B、C类构件都有具体的理论建模,且通过对甲板结构卷曲半径进行修正,从机理层面考虑各构件之间的耦合效应,提高对甲板结构损伤的预报精度及大撞深等场景下的适用性。

(a) 工况2

通过图14和图15的对比可以发现,在碰撞角度一定的情况下,随着船艏的深入,参与变形的构件数量及程度也会不断增大,因此甲板结构整体的能量耗散曲线呈上升趋势。且针对同一块甲板,在撞深一定的情况下,撞击角度越小,能量耗散越大,这是由于小角度斜撞使被撞船参与变形的构件在纵向上范围更大,同时也说明,在吸收能量一定的情况下,90°正撞会造成最大的撞深,此时船体更容易发生破损、进水、货物泄露等情况,该场景最危险。

综上,解析预报结果与仿真结果对比良好,本文提出的甲板结构在楔形船艏大撞深、多角度碰撞场景下的解析计算公式准确合理。

取撞深与甲板结构沿撞深方向上总尺度的比值作为误差分析参考量,以甲板参与度最高的工况1～工况4为例,绘制不同方法在不同撞深阶段的误差分析对比表,如表3所示。

表3 误差对比表

从表3可知,在撞深与甲板沿撞深方向上总尺度的比值较大时,等效厚度方法精度越来越低,本文解析方法优势明显。当撞深与甲板构件尺度比值较小时,两种方法在大部分工况下的误差都较小。除个别工况,如工况1,本文解析公式误差最高,达到12.77%。结合图14及有限元仿真结果进一步观察发现,误差主要是由于在初期甲板从压溃褶皱到发生破损进而结构撕裂的过程中,解析方法对具体撕裂开始的点预报精度还有待提高。这也是解析方法一直面临的难点之一[20],通常可结合试验修正提出半经验公式来解决[21-22]。随着撞深增大,甲板变形模式以撕裂为主导,这一误差的影响会越来越小。其次,通过进一步分析产生最大误差的工况,提取了该点解析结果与仿真结果的具体数值进行比较,发现本文解析方法预报结果(1.04 MJ)与仿真结果(0.92 MJ)总体仍很接近,预报依然在合理范围,这对于工程实践是可以接受的。

因此,在大撞深大损伤的场景下,本文方法的预报精度远高于等效厚度法,更能满足实际工程需求。从结构优化的设计角度出发,根据本文解析公式可以在甲板设计阶段从机理层面针对构件尺寸对整体的影响进行定量分析,以满足不同的抗撞性能要求,而不是单纯将所有构件以涂抹板厚的方式计入分析过程。但本文解析公式相对复杂,对于小撞深或某些特定场景,等效厚度法以其简单便捷依然有一定的实用性。

4 结 论

本文对单层壳船体舷侧结构遭受楔形船艏正撞与斜撞场景下甲板结构的损伤变形机理进行研究。提出一种预报甲板结构损伤的解析方法,并与数值结果、现有解析公式进行对比验证,得到以下结论:

(1) 本文考虑多角度斜撞场景,对甲板结构四类构件进行理论建模并推导结构抗力及能量耗散解析公式。通过从机理层面考虑各构件可能存在的耦合效应,针对甲板结构撕裂变形阶段下的卷曲半径进行修正。相较于以往等效厚度方法,本文解析方法适用性更好、精确度更高。

(2) 针对大撞深、多角度场景进行损伤预报时,构件可能存在多模式损伤演化,不能单纯参考传统结构损伤预报中采用的单一损伤模型,而是要进一步考虑各构件在实际变形过程中的演化过程,如本文提出的评估方法考虑了甲板从压溃褶皱到撕裂变形模式的损伤演化。但对于具体损伤演化点的预报,未来可以结合经验公式及模型试验进行进一步研究。

(3) 在不同撞深与甲板沿撞深方向上总尺度的比值下,本文方法的预报结果总体趋势准确,可满足实际工程需求。从结构优化的角度出发,本文解析公式包含构件厚度、高度、间距等具体尺寸,可以从机理层面针对构件尺寸对整体的影响进行定量分析,以满足不同的抗撞性能要求。但本文解析公式相对复杂,对于某些场景,等效厚度法以其简单便捷依然有实用性。