四次累积发放神经元同宿环及周期解的存在性和稳定性分析
2023-12-18吴建梅徐洁琼王俊杰徐启祥
吴建梅, 徐洁琼, 王俊杰, 徐启祥
(广西大学 数学与信息科学学院,南宁 500064)
神经元是神经系统的基本结构和功能单元,神经系统的放电活动主要表现为神经元产生和传输电脉冲的过程,神经信息主要通过神经元放电活动的节律模式来进行编码。最早的神经元模型由Hodgkin和Huxley在1952年提出,称为Hodgkin-Huxley(H-H)模型[1]。为便于数学理论分析、高效计算以及大规模神经网络的模拟,许多学者对该模型进行了改进。其中,累积发放神经元模型(IF模型)是一类比较常用的简化模型,这类模型能够模拟真实神经元丰富和复杂的放电行为且维数较低。其中平方自适应IF模型(Izhikevich模型)、自适应指数IF(integrate-and-fire)神经元模型、四次IF神经元模型等模型是其中的代表。Breete等[2]用自适应指数IF神经元模型成功拟合了椎体神经元真实的放电记录。Izhikevich等[3]用Izhikevich神经元模型对哺乳动物的丘脑皮层系统进行了模拟。四次IF神经元模型不仅能产生自适应指数IF神经元模型和Izhikevich神经元都能产生的放电模式,还能产生Phasic相应、放电频率自适应、阈下振荡等放电模式[4]。本文选择四次累积发放神经元模型为代表来研究非光滑神经元的动力学行为,将理论分析四次IF模型的周期解的存在性和稳定性。
IF神经元模型具有重置过程,因此,该类模型具有非光滑特性,属于非光滑动力系统的范畴。四次IF神经元模型属于第一类非光滑系统,即,脉冲动力系统。脉冲动力系统广泛存在于自然、社会与实际工程背景中,涉及到众多领域。例如,机械系统中典型的碰撞振动系统[5]、电路中的开关切换[6]、阈值限定[7]等,以及生物力学领域中的害虫治理[8]、种群动力学模型[9-10]、微生物生长模型[11]等。对脉冲动力系统周期解的研究,往往会选择不连续面或时间面为庞加莱截面,通过重置映射和光滑流的复合得到一个庞加莱映射,把脉冲动力系统周期解的存在性转化为庞加莱映射的不动点的存在性[12]。Yang等[13]提出HR混合模型,应用庞加莱映射不动点理论给出了周期解的存在性和稳定性分析,并讨论了其周期增加的分岔和混沌现象;He等[14]研究了具有状态依赖脉冲效应的FHN模型的动力学行为,利用几何分析构造了不同条件下的庞加莱映射,通过庞加莱映射不动点理论和几何分析技术,得到了脉冲神经元模型周期解的存在性和稳定性的条件;Yi等[15]研究了具有状态依赖脉冲效应的Izhikevich模型,通过脉冲动力系统的理论、庞加莱截面和常微分方程几何理论等给出周期解的存在性和稳定性充分条件,并用数值仿真验证了主要结果。在此基础上,本文将利用非光滑动力学理论和不动点理论,通过证明四次累积发放神经元模型1-阶同宿环的存在性,从而证明同宿分岔后,1-阶周期解(1-阶簇放电)的存在性。
1 模型、相关定义及方法
考虑四次累积发放神经元模型

(1)
当v到达某一给定阈值时,系统具有如下重置过程,即,
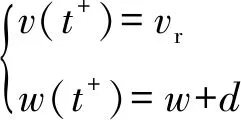
(2)
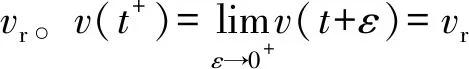
方便起见,接下来用M表示阈值线v=vth,则M为脉冲集,用L表示重置线v=vr,故L为M对应的相集。用Ψ表示脉冲函数,即存在A(vA,wA)∈M,有Ψ(vA)=vr,Ψ(wA)=wA+d,用φ表示系统(1)、(2)相应的流。
定义1:若O(v,w)为系统(1)、(2)的轨线,(v(t+),w(t+))∈L为O上的点(v(t),w(t))∈M对应的重置点,并且存在非负正数n、正整数k,使得(vn(t+),wn(t+))=(vn+k(t+),wn+k(t+)),则称O(v,w)为k-阶周期解。k=1时,为1-阶周期解。
定义2:如果存在A∈L,当t>0,有φ(A,t)=B∈M,且脉冲效应后B重置到A点,则轨迹φ(A,t)+脉冲线BA称为1-阶环。
若1-阶环有一个奇点,则称为1-阶奇异环。此外,若1-阶奇异环的奇点为鞍点,则称为1-阶鞍点同宿环。1-阶鞍点同宿环由鞍点、鞍点不稳定流形、鞍点稳定流形和脉冲线四部分组成。
定义3: 假设φ(A,t)是系统(1)、(2)的一个1-阶周期解。任意ε>0,存在δ>0,若对任意A1∈U(A,δ)∩L,存在t0>0,当t>t0,有ρ(φ(A,t),φ(A1,t))<ε,则称1-阶周期解φ(A,t)是轨道渐近稳定的。其中U表示邻域,ρ表示距离。
构造庞加莱映射:
可以构造两种庞加莱映射来讨论系统(1)、(2)的动力学行为。
(i) 以重置面为庞加莱截面S={(v,w)|v=vr}。
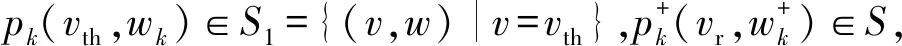
(ii) 以阈值面为庞加莱截面S1={(v,w)|v=vth}。
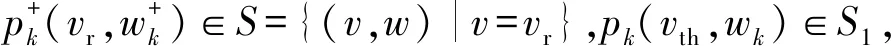
方法:四阶龙格库塔法,时间步长为0.000 1,软件为XPPAUT和MTALAB。
2 系统的动力学行为分析
2.1 v1(A1) 鞍点E2(v2,w2)的不稳定流形MU与脉冲集M相交,交点用A(vA,wA)表示。鞍点E2(v2,w2)的稳流形MS与重置线L的交点为B(vB,wB),如图1所示。图中字母Lv为v-零值线,Lw为w-零值线,虚线表示脉冲线。后面的示意图中,不同字母所表示相同的含义。
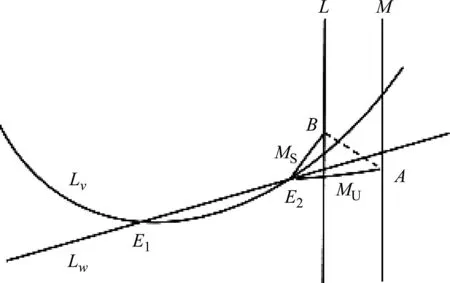
图1 情形(A1)时系统(1)、(2)的1-阶同宿环
(A2) 平衡点E1为稳定点,平衡点E2为鞍点。鞍点E2的不稳定流形MU与脉冲集M相交,其交点用A(vA,wA)表示;鞍点E2的稳定流形MS与集合L的交点用B(vB,wB)表示,如图2所示。
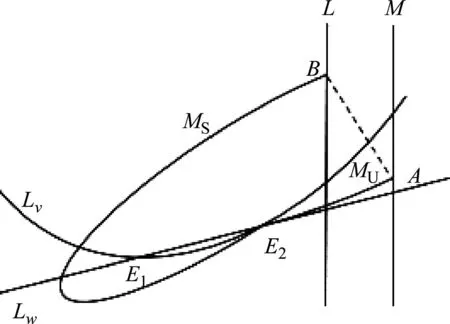
图2 情形(A2)时系统(1)、(2)的1-阶同宿环
(A3) 平衡点E1为不稳定点,E2为鞍点。鞍点E2的不稳流形MU与脉冲集M相交,交点用A(vA,wA)表示;集合L与MS的交点为B(vB,wB),如图3所示。
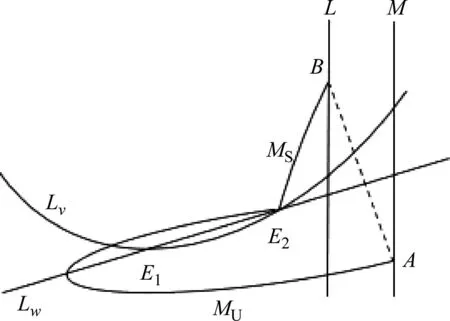
图3 情形(A3)时系统(1)、(2)的1-阶同宿环
2.2 v1(B1) 鞍点E2的不稳定流形MU与脉冲集M相交于点A(vA,wA),且wA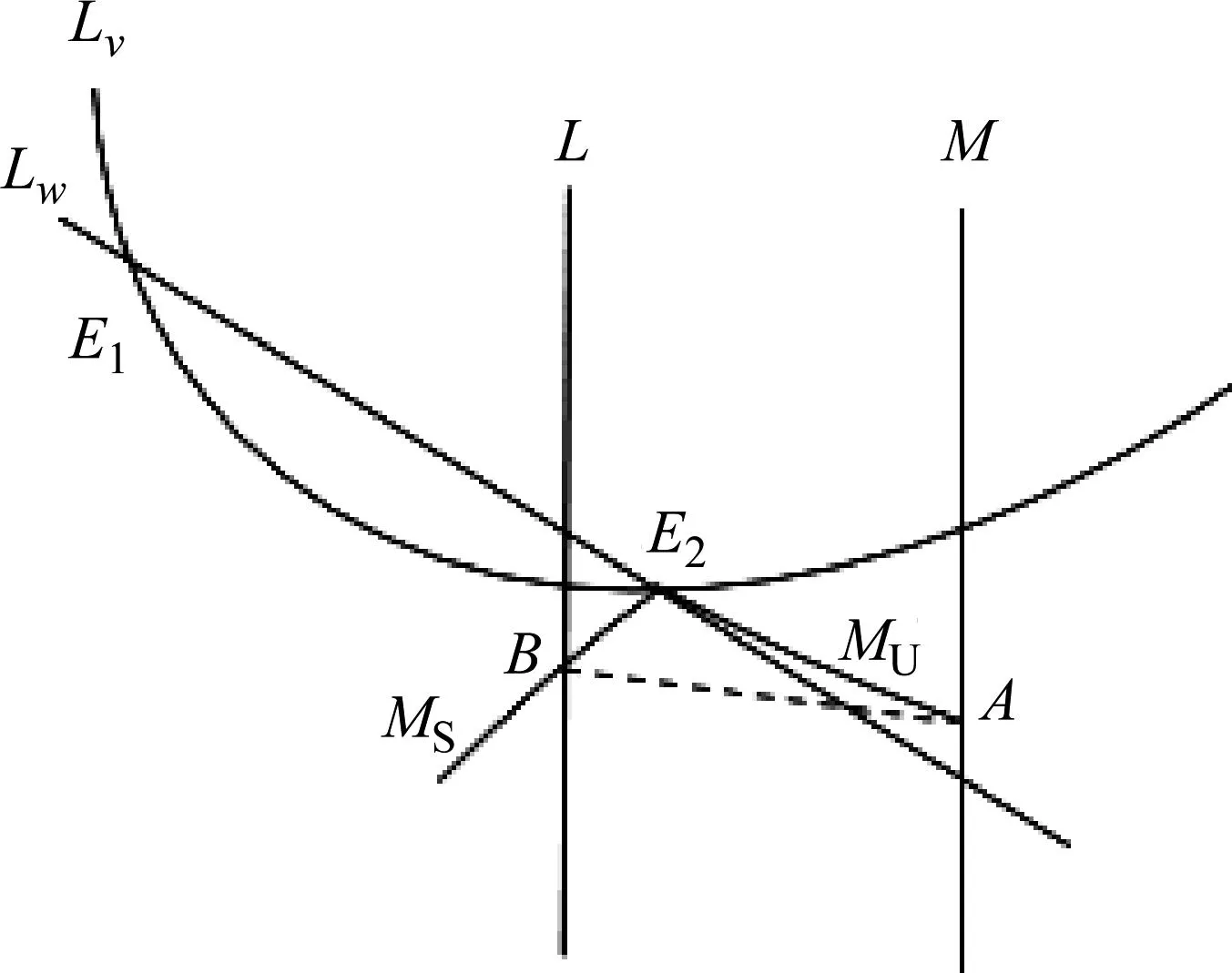
图4 情形(B1)时系统(1)、(2)的1-阶同宿环
(B2)E1为稳定平衡点,E2为鞍点。E2的不稳定流形MU与脉冲集M相交于点A(vA,wA),且wA>wE2;E2的稳定流形MS与L相交于点B(vB,wB),且wB>wE2,如图5所示。
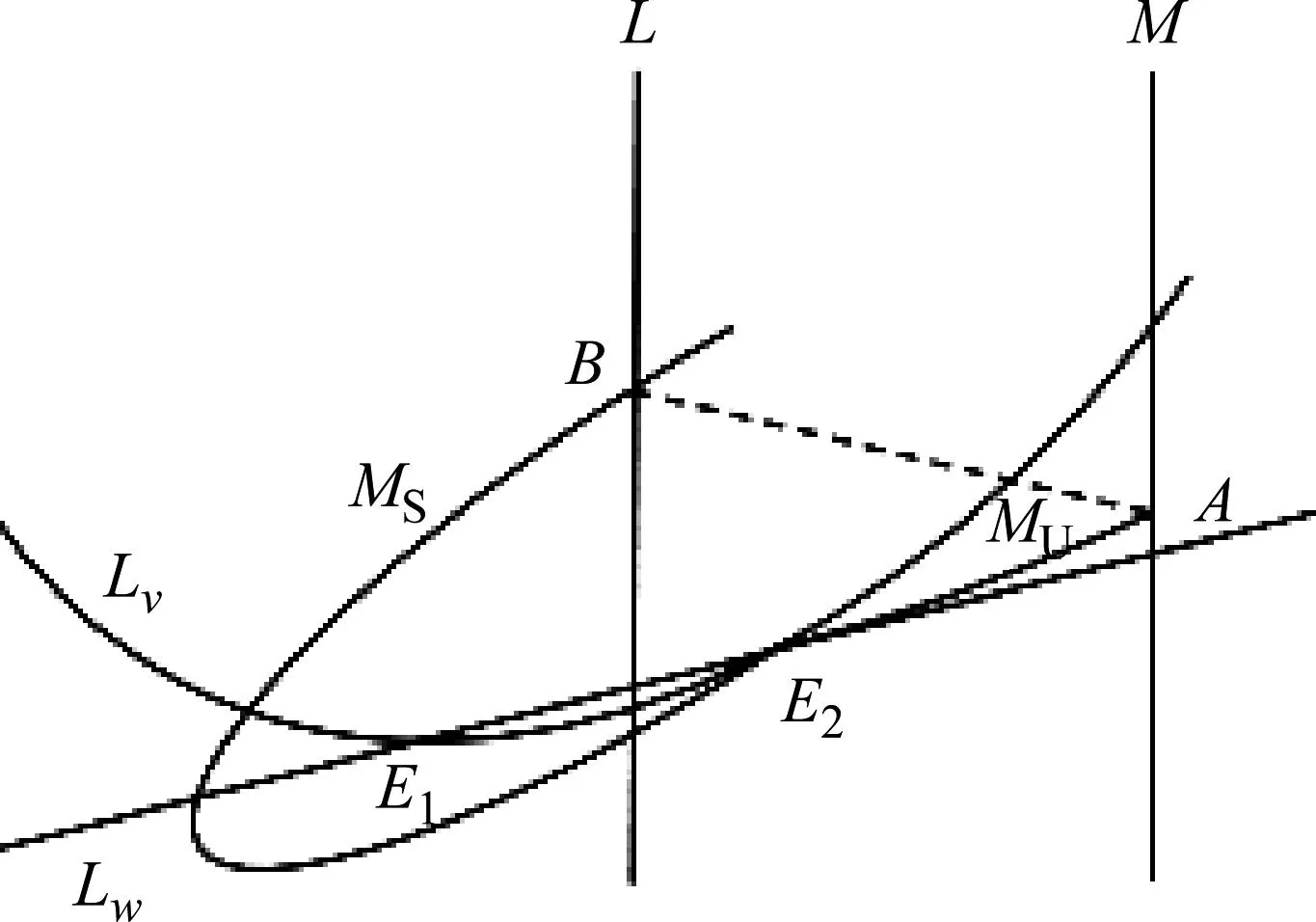
图5 情形(B2)时系统(1)、(2)的1-阶同宿环
(B3)E1为不稳定平衡点,E2为鞍点。鞍点E2的不稳流形MU与脉冲集M相交,交点用A(vA,wA)表示;鞍点E2的稳定流形MS与重置线L的交点为B(vB,wB),且wA≤wB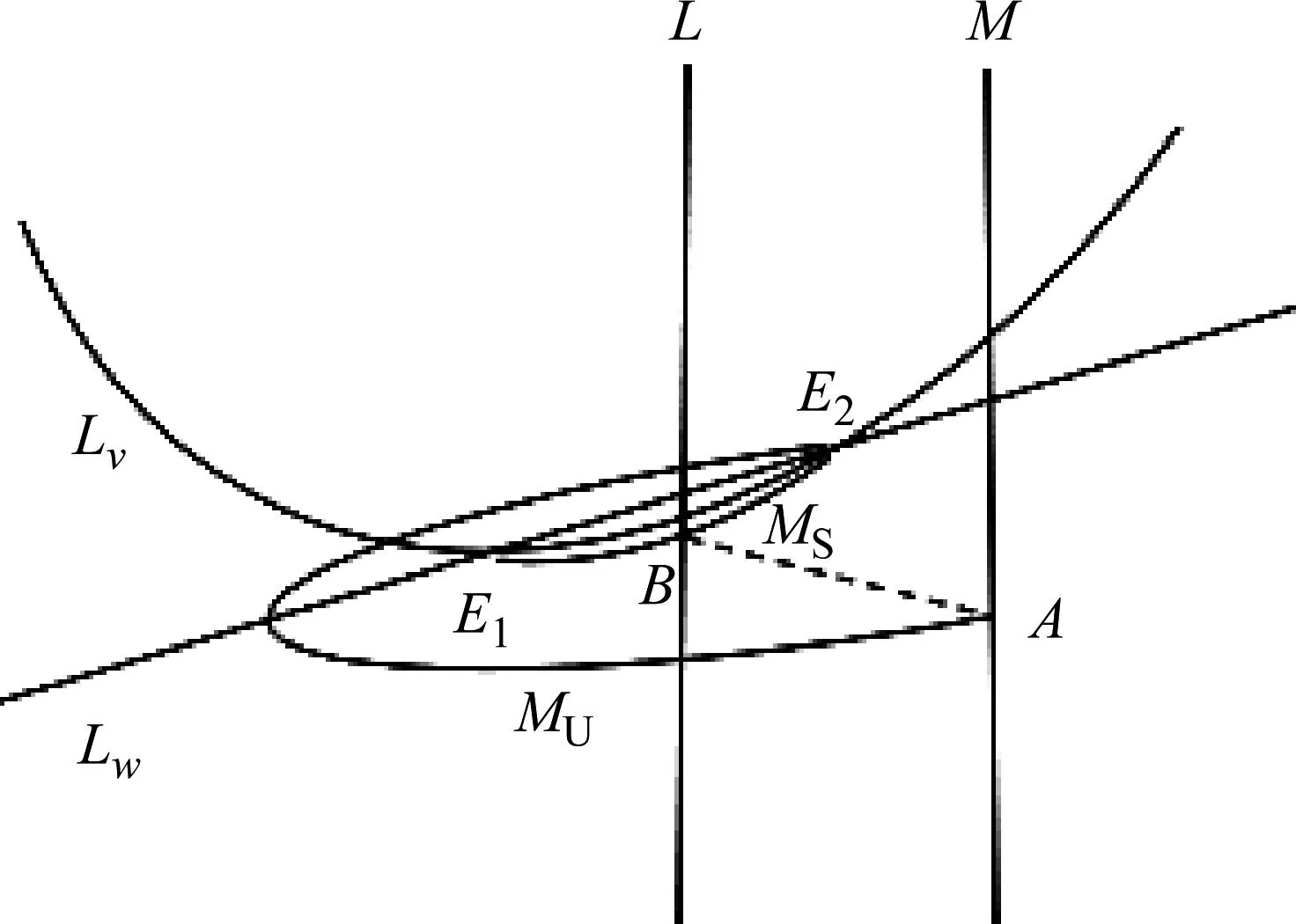
图6 情形(B3)时系统(1)、(2)的1-阶同宿环
对于以上六种情形,存在d*使得脉冲效应后点A映射到点B,即Ψ(wA,d*)=wA+d*=wB,则BE2、E2A和脉冲线AB构成一个通过鞍点E2的环,因此系统(1)、(2)存在一个同宿环。如若选取合适的参数,则存在d*≥0使得wB=wA+d*,即系统(1)、(2)存在1-阶同宿环。我们有如下定理。
定理1:对于情形(A1)、(A2)、(A3)、(B1)、(B2)、(B3),选取适当的参数,则存在d*≥0使得系统(1)、(2)存在一个1-阶同宿环。
接下来,选取d为分岔参数讨论同宿分岔问题。当d改变,1-阶同宿环消失,一个1-阶周期解出现。不失一般性,我们考虑d*>0。
定理2:对于情形(A1),当0≤dΨ(wC1,d)时,则系统(1)、(2)的同宿环消失,分岔出一个轨道渐近稳定的1-阶周期解,而且这个1-阶周期解是唯一的。
证明:作图如图7所示。对于定理中给出的条件,则可得到以下序列:
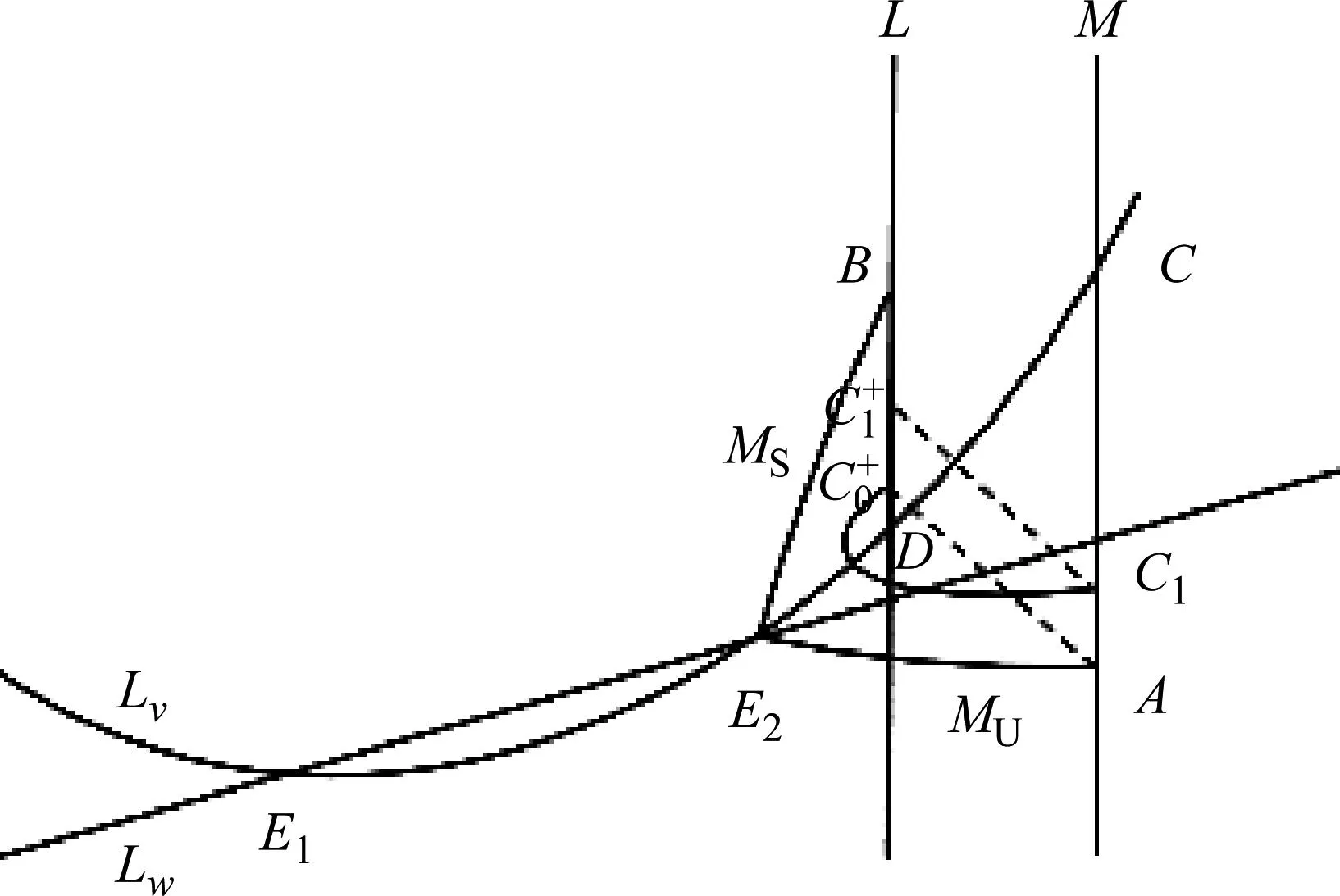
图7 情形(A1)时系统(1)、(2)的1-阶周期解的存在性
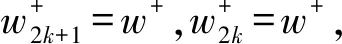
定理3:对于情形(A2)、(A3)、(B2)、(B3),当d>d*≥0,且wB证明:以情形(B2)为例,根据定理所给的条件作图如图8所示,则可得到如下序列
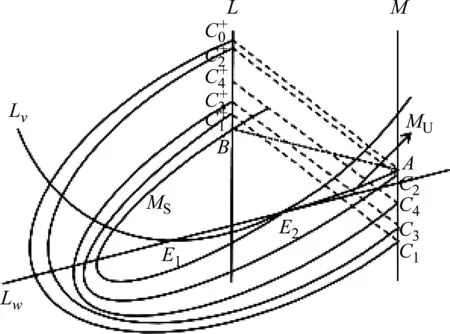
图8 情形(B2),系统(1)、(2)的1-阶周期解的存在性
w1当k→∞时,存在w∈(w1,wA)使得w2k+1=w,w2k=w,故系统(1)、(2)存在唯一一个轨道渐近稳定的1-阶周期解。证明完毕。对于情形(A2)、(A3)、(B3),证明类似,在此不重复证明。
对于(B1)情形,当d改变时,1-阶同宿环消失,当0≤d定理4:对于(B1)情形,当0≤d证明:作图如图9所示,点C为w-零值线与阈值线M:v=vth的交点。以v=vth为庞加莱截面,取初始点位于v=vth,且w0∈[wC,wA],则有w1=α(w0)∈M。由于d≥0,故φ(wC+d)≥wC。
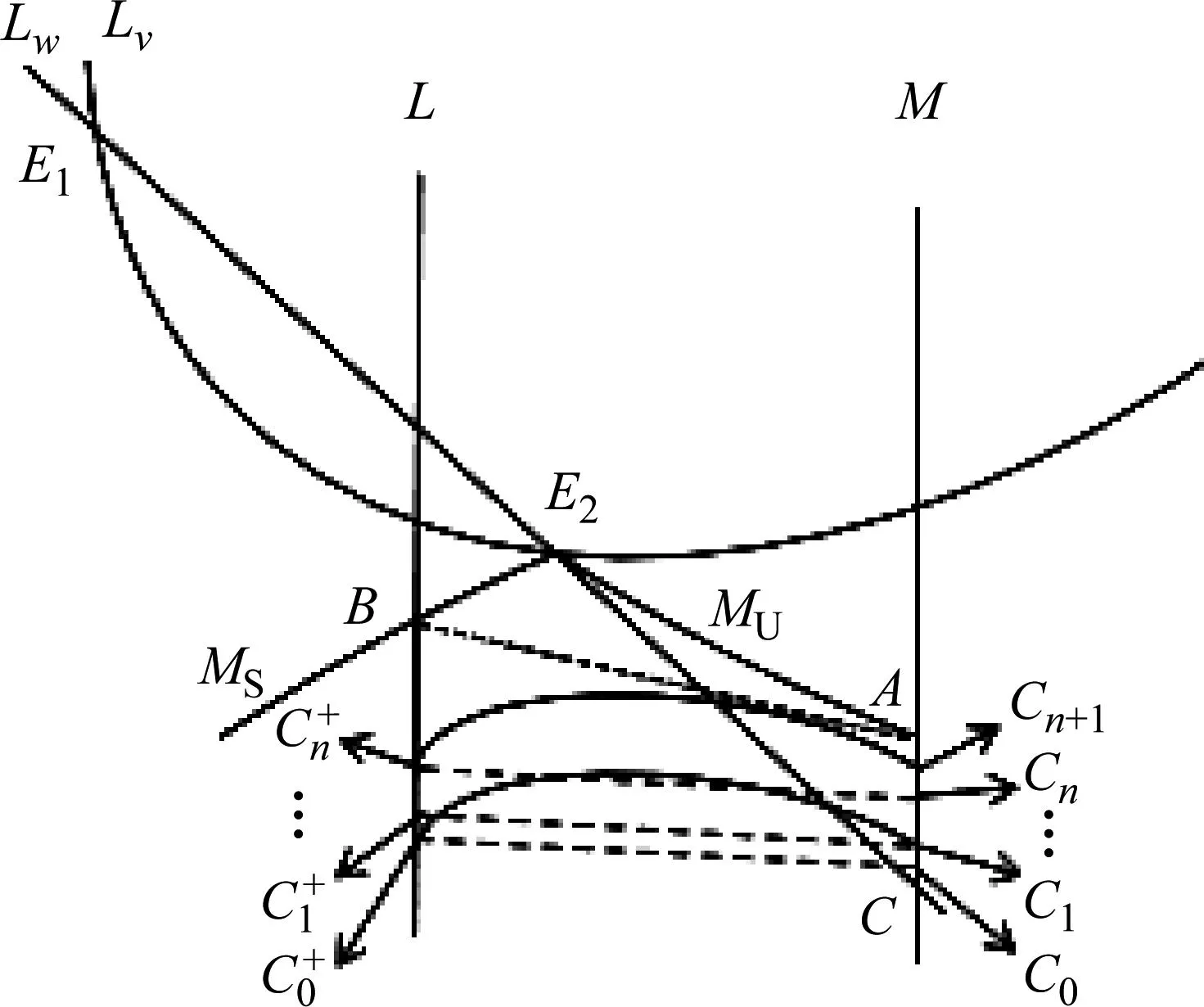
图9 情形(B1),系统(1)、(2)的1-阶周期解的存在性
(i)w0=w1,则有唯一一点w0∈[wC,wA]使得α(w0)=w0,故系统(1)、(2)存在唯一1-阶周期解,且是轨道渐近稳定的。
(ii)w0(iii)w0>w1,则有wC<…接下来我们将给出1-阶周期解轨道渐近稳定的一般性判定定理。
定理5:当d≥0时,设O(v(t),w(t))为系统(1)、(2)的周期为T的1-阶周期解,其初始点为Z+(vr,w*),且与阈值线v=vth相交于点Z(vth,w*-d)。若μ<1,则O(v(t),w(t))是轨道渐近稳定的,其中
证明:根据参考文献[16],由系统(1)、(2)可取
P=v4+2av-w+i,Q=a(bv-w),
f=Δv=vr-vth,h=Δw=d,φ=v-vth,
(v(T),w(T))=(vth,w*-d),
(v(T+),w(T+))=(vr,w*)。
则有
则可得到:
Δ1=
且有
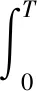
则可得Floquent乘子:
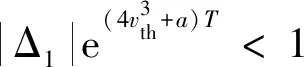
3 数值仿真
在此章中,运用数值仿真的手段去验证理论的结果,以情形(A1)和情形(B2)为例。当选取参数i=4,a=4,b=2时,则系统(1)、(2)平衡点分别为E1(-1.491 5,-2.983 1),E2(-0.708 71,-1.417 40),取vr=-0.5,vth=0.5,则有v1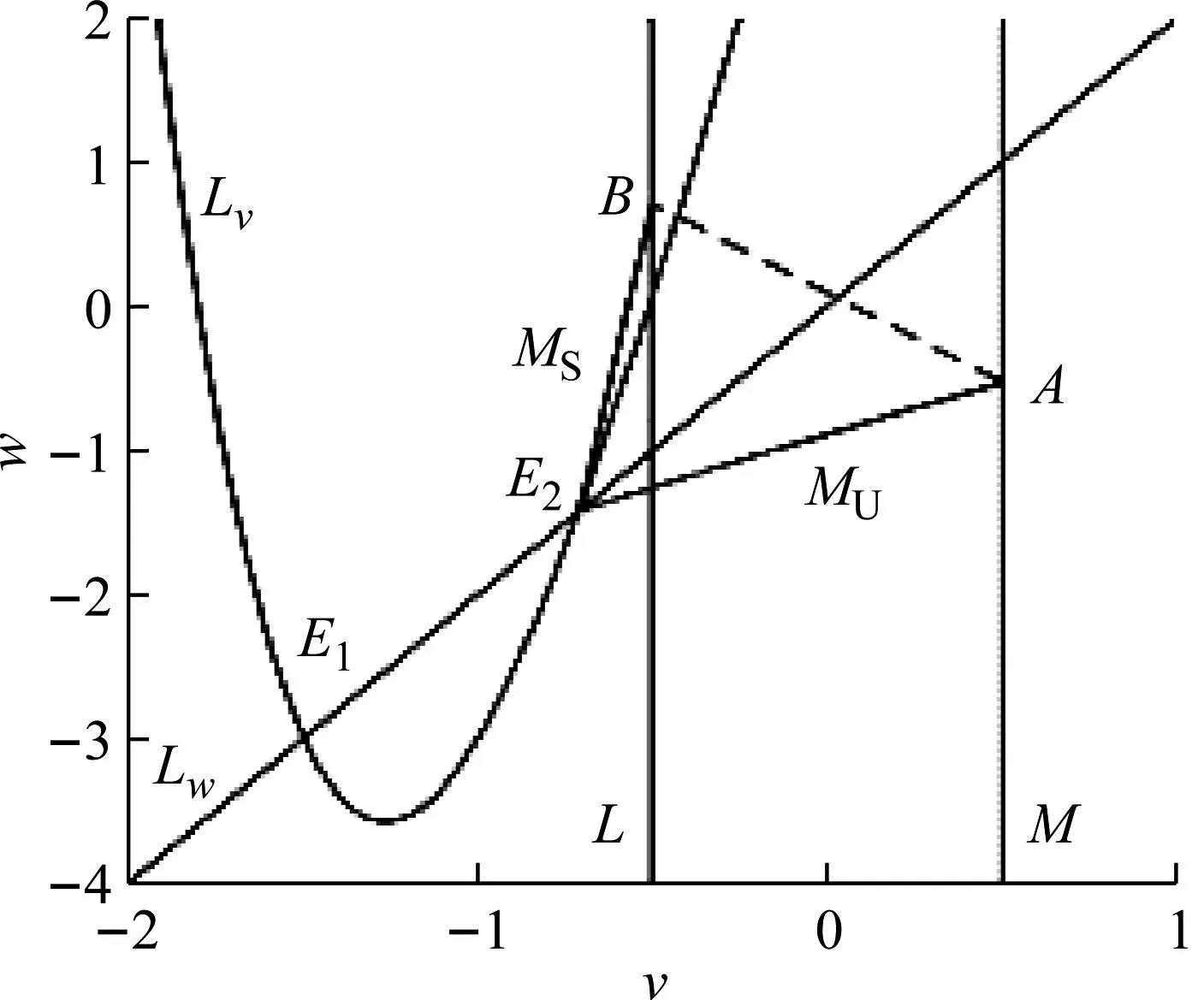
(a)
对于情形(B2),当选取参数i=0.3,a=1,b=1.24时,则系统(1)、(2)的两个平衡点分别为E1(-0.685 81,-0.850 40),E2(-0.447 51,-0.554 91),重置值和阈值分别取vr=-0.5,vth=-0.3,则有v1d*时,由定理3可知系统(1)、(2)的同宿环消失,一个轨道渐近稳定的1-阶周期解出现,如图11(b)所示。其中1-阶周期解由字母O表示。
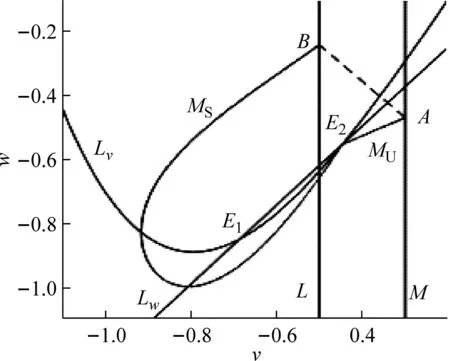
(a)
4 结 论
(1) 讨论了系统(1)、(2)存在两个平衡点(一个为鞍点,一个非鞍点)时的同宿分岔。考虑E1(v1,w1)为非鞍点的平衡点,E2(v2,w2)为鞍点,且有v1(2) 仅针对系统具有两个平衡点的情形进行了讨论,当系统具有其它动力学特性情形下,周期解的存在性和稳定性的分析,以及多周期峰放电和簇放电存在性的研究将在后续工作中开展。
(A1) 鞍点E2(v2,w2)的不稳定流形MU与脉冲集M相交,交点用A(vA,wA)表示。鞍点E2(v2,w2)的稳流形MS与重置线L的交点为B(vB,wB),如图1所示。图中字母Lv为v-零值线,Lw为w-零值线,虚线表示脉冲线。后面的示意图中,不同字母所表示相同的含义。

图1 情形(A1)时系统(1)、(2)的1-阶同宿环
(A2) 平衡点E1为稳定点,平衡点E2为鞍点。鞍点E2的不稳定流形MU与脉冲集M相交,其交点用A(vA,wA)表示;鞍点E2的稳定流形MS与集合L的交点用B(vB,wB)表示,如图2所示。

图2 情形(A2)时系统(1)、(2)的1-阶同宿环
(A3) 平衡点E1为不稳定点,E2为鞍点。鞍点E2的不稳流形MU与脉冲集M相交,交点用A(vA,wA)表示;集合L与MS的交点为B(vB,wB),如图3所示。

图3 情形(A3)时系统(1)、(2)的1-阶同宿环
2.2 v1(B1) 鞍点E2的不稳定流形MU与脉冲集M相交于点A(vA,wA),且wA
图4 情形(B1)时系统(1)、(2)的1-阶同宿环
(B2)E1为稳定平衡点,E2为鞍点。E2的不稳定流形MU与脉冲集M相交于点A(vA,wA),且wA>wE2;E2的稳定流形MS与L相交于点B(vB,wB),且wB>wE2,如图5所示。

图5 情形(B2)时系统(1)、(2)的1-阶同宿环
(B3)E1为不稳定平衡点,E2为鞍点。鞍点E2的不稳流形MU与脉冲集M相交,交点用A(vA,wA)表示;鞍点E2的稳定流形MS与重置线L的交点为B(vB,wB),且wA≤wB
图6 情形(B3)时系统(1)、(2)的1-阶同宿环
对于以上六种情形,存在d*使得脉冲效应后点A映射到点B,即Ψ(wA,d*)=wA+d*=wB,则BE2、E2A和脉冲线AB构成一个通过鞍点E2的环,因此系统(1)、(2)存在一个同宿环。如若选取合适的参数,则存在d*≥0使得wB=wA+d*,即系统(1)、(2)存在1-阶同宿环。我们有如下定理。
定理1:对于情形(A1)、(A2)、(A3)、(B1)、(B2)、(B3),选取适当的参数,则存在d*≥0使得系统(1)、(2)存在一个1-阶同宿环。
接下来,选取d为分岔参数讨论同宿分岔问题。当d改变,1-阶同宿环消失,一个1-阶周期解出现。不失一般性,我们考虑d*>0。
定理2:对于情形(A1),当0≤dΨ(wC1,d)时,则系统(1)、(2)的同宿环消失,分岔出一个轨道渐近稳定的1-阶周期解,而且这个1-阶周期解是唯一的。
证明:作图如图7所示。对于定理中给出的条件,则可得到以下序列:

图7 情形(A1)时系统(1)、(2)的1-阶周期解的存在性
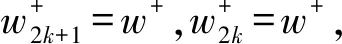
定理3:对于情形(A2)、(A3)、(B2)、(B3),当d>d*≥0,且wB证明:以情形(B2)为例,根据定理所给的条件作图如图8所示,则可得到如下序列

图8 情形(B2),系统(1)、(2)的1-阶周期解的存在性
w1当k→∞时,存在w∈(w1,wA)使得w2k+1=w,w2k=w,故系统(1)、(2)存在唯一一个轨道渐近稳定的1-阶周期解。证明完毕。对于情形(A2)、(A3)、(B3),证明类似,在此不重复证明。
对于(B1)情形,当d改变时,1-阶同宿环消失,当0≤d定理4:对于(B1)情形,当0≤d证明:作图如图9所示,点C为w-零值线与阈值线M:v=vth的交点。以v=vth为庞加莱截面,取初始点位于v=vth,且w0∈[wC,wA],则有w1=α(w0)∈M。由于d≥0,故φ(wC+d)≥wC。

图9 情形(B1),系统(1)、(2)的1-阶周期解的存在性
(i)w0=w1,则有唯一一点w0∈[wC,wA]使得α(w0)=w0,故系统(1)、(2)存在唯一1-阶周期解,且是轨道渐近稳定的。
(ii)w0(iii)w0>w1,则有wC<…接下来我们将给出1-阶周期解轨道渐近稳定的一般性判定定理。
定理5:当d≥0时,设O(v(t),w(t))为系统(1)、(2)的周期为T的1-阶周期解,其初始点为Z+(vr,w*),且与阈值线v=vth相交于点Z(vth,w*-d)。若μ<1,则O(v(t),w(t))是轨道渐近稳定的,其中
证明:根据参考文献[16],由系统(1)、(2)可取
P=v4+2av-w+i,Q=a(bv-w),
f=Δv=vr-vth,h=Δw=d,φ=v-vth,
(v(T),w(T))=(vth,w*-d),
(v(T+),w(T+))=(vr,w*)。
则有
则可得到:
Δ1=
且有
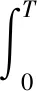
则可得Floquent乘子:
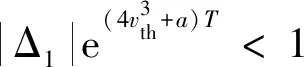
3 数值仿真
在此章中,运用数值仿真的手段去验证理论的结果,以情形(A1)和情形(B2)为例。当选取参数i=4,a=4,b=2时,则系统(1)、(2)平衡点分别为E1(-1.491 5,-2.983 1),E2(-0.708 71,-1.417 40),取vr=-0.5,vth=0.5,则有v1
(a)
对于情形(B2),当选取参数i=0.3,a=1,b=1.24时,则系统(1)、(2)的两个平衡点分别为E1(-0.685 81,-0.850 40),E2(-0.447 51,-0.554 91),重置值和阈值分别取vr=-0.5,vth=-0.3,则有v1d*时,由定理3可知系统(1)、(2)的同宿环消失,一个轨道渐近稳定的1-阶周期解出现,如图11(b)所示。其中1-阶周期解由字母O表示。

(a)
4 结 论
(1) 讨论了系统(1)、(2)存在两个平衡点(一个为鞍点,一个非鞍点)时的同宿分岔。考虑E1(v1,w1)为非鞍点的平衡点,E2(v2,w2)为鞍点,且有v1(2) 仅针对系统具有两个平衡点的情形进行了讨论,当系统具有其它动力学特性情形下,周期解的存在性和稳定性的分析,以及多周期峰放电和簇放电存在性的研究将在后续工作中开展。
(B1) 鞍点E2的不稳定流形MU与脉冲集M相交于点A(vA,wA),且wA 图4 情形(B1)时系统(1)、(2)的1-阶同宿环 (B2)E1为稳定平衡点,E2为鞍点。E2的不稳定流形MU与脉冲集M相交于点A(vA,wA),且wA>wE2;E2的稳定流形MS与L相交于点B(vB,wB),且wB>wE2,如图5所示。 图5 情形(B2)时系统(1)、(2)的1-阶同宿环 (B3)E1为不稳定平衡点,E2为鞍点。鞍点E2的不稳流形MU与脉冲集M相交,交点用A(vA,wA)表示;鞍点E2的稳定流形MS与重置线L的交点为B(vB,wB),且wA≤wB 图6 情形(B3)时系统(1)、(2)的1-阶同宿环 对于以上六种情形,存在d*使得脉冲效应后点A映射到点B,即Ψ(wA,d*)=wA+d*=wB,则BE2、E2A和脉冲线AB构成一个通过鞍点E2的环,因此系统(1)、(2)存在一个同宿环。如若选取合适的参数,则存在d*≥0使得wB=wA+d*,即系统(1)、(2)存在1-阶同宿环。我们有如下定理。 定理1:对于情形(A1)、(A2)、(A3)、(B1)、(B2)、(B3),选取适当的参数,则存在d*≥0使得系统(1)、(2)存在一个1-阶同宿环。 接下来,选取d为分岔参数讨论同宿分岔问题。当d改变,1-阶同宿环消失,一个1-阶周期解出现。不失一般性,我们考虑d*>0。 定理2:对于情形(A1),当0≤d 证明:作图如图7所示。对于定理中给出的条件,则可得到以下序列: 图7 情形(A1)时系统(1)、(2)的1-阶周期解的存在性 定理3:对于情形(A2)、(A3)、(B2)、(B3),当d>d*≥0,且wB 证明:以情形(B2)为例,根据定理所给的条件作图如图8所示,则可得到如下序列 图8 情形(B2),系统(1)、(2)的1-阶周期解的存在性 w1 当k→∞时,存在w∈(w1,wA)使得w2k+1=w,w2k=w,故系统(1)、(2)存在唯一一个轨道渐近稳定的1-阶周期解。证明完毕。对于情形(A2)、(A3)、(B3),证明类似,在此不重复证明。 对于(B1)情形,当d改变时,1-阶同宿环消失,当0≤d 定理4:对于(B1)情形,当0≤d 证明:作图如图9所示,点C为w-零值线与阈值线M:v=vth的交点。以v=vth为庞加莱截面,取初始点位于v=vth,且w0∈[wC,wA],则有w1=α(w0)∈M。由于d≥0,故φ(wC+d)≥wC。 图9 情形(B1),系统(1)、(2)的1-阶周期解的存在性 (i)w0=w1,则有唯一一点w0∈[wC,wA]使得α(w0)=w0,故系统(1)、(2)存在唯一1-阶周期解,且是轨道渐近稳定的。 (ii)w0 (iii)w0>w1,则有wC<… 接下来我们将给出1-阶周期解轨道渐近稳定的一般性判定定理。 定理5:当d≥0时,设O(v(t),w(t))为系统(1)、(2)的周期为T的1-阶周期解,其初始点为Z+(vr,w*),且与阈值线v=vth相交于点Z(vth,w*-d)。若μ<1,则O(v(t),w(t))是轨道渐近稳定的,其中 证明:根据参考文献[16],由系统(1)、(2)可取 P=v4+2av-w+i,Q=a(bv-w), f=Δv=vr-vth,h=Δw=d,φ=v-vth, (v(T),w(T))=(vth,w*-d), (v(T+),w(T+))=(vr,w*)。 则有 则可得到: Δ1= 且有 则可得Floquent乘子: 在此章中,运用数值仿真的手段去验证理论的结果,以情形(A1)和情形(B2)为例。当选取参数i=4,a=4,b=2时,则系统(1)、(2)平衡点分别为E1(-1.491 5,-2.983 1),E2(-0.708 71,-1.417 40),取vr=-0.5,vth=0.5,则有v1 (a) 对于情形(B2),当选取参数i=0.3,a=1,b=1.24时,则系统(1)、(2)的两个平衡点分别为E1(-0.685 81,-0.850 40),E2(-0.447 51,-0.554 91),重置值和阈值分别取vr=-0.5,vth=-0.3,则有v1 (a) (1) 讨论了系统(1)、(2)存在两个平衡点(一个为鞍点,一个非鞍点)时的同宿分岔。考虑E1(v1,w1)为非鞍点的平衡点,E2(v2,w2)为鞍点,且有v1 (2) 仅针对系统具有两个平衡点的情形进行了讨论,当系统具有其它动力学特性情形下,周期解的存在性和稳定性的分析,以及多周期峰放电和簇放电存在性的研究将在后续工作中开展。



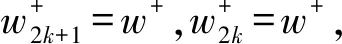


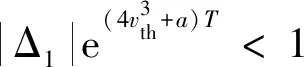
3 数值仿真


4 结 论
