单流体空化模型在水下爆炸诱导空化问题中的对比分析

金泽宇, 殷彩玉, 孔祥韶

(1. 武汉理工大学 绿色智能江海直达船舶与邮轮游艇研究中心, 武汉 430063; 2. 华中科技大学 船舶与海洋工程学院, 武汉 430074)

水下爆炸诱导空化主要包括自由面附近的片空化和结构表面附近的局部空化。在水下爆炸后,冲击波在水中传播并与自由面或水下结构相互作用,自由面或结构的运动与变形使水中产生稀疏波。当入射波、反射波、稀疏波的压力与静水压在某点的叠加压力值小于饱和蒸汽压,流体就会发生空化。由于片空化问题中水的重力作用和局部空化问题中结构的减速作用,空化会溃灭,产生以冲击波或者流体动量的形式加载到舰船或水下航行器的作用力。典型片空化和局部空化示意图,如图1所示。空化溃灭载荷是一种源自水下爆炸的典型的破坏载荷。

水下爆炸载荷与不同边界相互作用产生的空化得到广泛研究。Kennard[1]在双线弹性流体中理论描述了空化。他的研究表明,当流体压力小于空化极限时,会产生空化,空化的边界或者是以超声速运动的破水波,或者形成保持静止的自由面,或者退化为以亚声速运动的闭合波。根据双线弹性流体模型,研究人员对水下冲击波与悬浮在自由面的平板相互作用产生的空化效应[2],水下冲击波与线弹簧支撑平板[3]、厚弹性板[4]、夹芯结构[5]相互作用产生的空化效应建立了理论模型。Schiffer等[6]和Feng等[7]搭建了透明水激波管试验模型,开展了系列试验研究,记录了近壁面空化的初生、扩展及溃灭过程。

数值模拟是研究空化的重要手段。典型的空化包括单流体空化模型和双流体空化模型。双流体模型假设汽相和液相在流体域中同时存在,由独立的微分方程控制,其控制方程数量是单流体模型的两倍。双流体空化模型能够考虑质量/能量转化、热传递、表面张力等。但两相流的一些初始条件很难直接获取。典型的双流体模型包括4方程模型[8-9]、6方程模型[10]和5方程模型[11]等。单流体模型假设汽液混合物宏观表现为单一流体,遵循统一的状态方程,因此只需要求解一套守恒方程,其难点是构建合理的混合物状态方程。典型的单流体模型包括截断模型,修正的Schmidt模型[12],等熵空化流模型[13]等。单流体模型由于构造简单,在水下爆炸问题中得到广泛应用[14-16]。但在应用单流体空化模型在水下爆炸问题时,不同模型究竟有多大差异仍存疑。

基于上述问题,本文建立经典水下爆炸问题的数值模型,对比单流体空化模型的截断模型,修正的Schmidt模型,等熵空化流模型的计算结果,得到不同空化模型的差异,为应用单流体模型求解水下爆炸问题提供依据。

1 空化模型

1.1 常态水状态方程

水下爆炸问题水通常采用Tait状态方程描述

(1)

式中:ρ为流体的密度;p为流体的压力;参考密度ρ0= 1 000 kg/m3;常数A= 1.0 ×105Pa;常数B= 3.31 ×108Pa; 常数N= 7.15。Tait状态方程在压力小于20 000 atm都可以描述水的状态。

在水的压力较小时,可将Tait状态方程线性化,可得到线性方程描述水

(2)

作为Tait状态方程的简化模型,线性方程具有求解简单,计算效率高等优点,可用于关于远场冲击波输入的问题。其中ρ0、p0和c0为初始给定密度、压力和相应的声速。此方程具有在水发生空化前声速为常数的特点。

1.2 空化流状态方程

截断模型可以表示成

(3)

式中,饱和蒸汽压psat可取2 068.5 Pa。

修正Schmidt模型可以表示成

p=

(4)

式中:饱和蒸汽压psat=2 068.5 Pa; 正压参数pε= 1×10-9Pa;α为孔隙分数。混合流体中:水蒸气密度ρg= 0.08 kg/m3; 水蒸气声速ag=190 m/s2; 液态水密度ρl= 999.958 6 kg/m3; 液态水声速al=1 538.2 m/s2。pgl可由下式确定

(5)

等熵空化流模型可以表示成

(6)

(7)

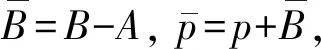
(8)

将不同空化模型运用MATLAB编程,并画出压力小于饱和蒸汽压的压力密度曲线,如图2所示。当计算压力小于饱和蒸汽压时,截断模型(Cut Off)的压力保持在饱和蒸汽压,而修正的Schmidt模型(M-Schmidt)和等熵空化流模型(Isentropic)随着密度降低压力迅速下降。从图2可知,M-Schmidt模型在较小的密度变化条件下,下降得更加迅速,而Isentropic模型表现出较为平滑的曲线。在压力小于饱和蒸汽压且大于修正Schmidt模型的截断压力pε时,相同密度条件下,运用M-Schmidt模型获得的压力小于Isentropic模型。

2 计算实例

本章开展水下冲击波与浮在自由面平板相互作用,水下冲击波与弹性支撑平板相互作用以及下冲击波与水背衬平板相互作用模拟。欧拉方程采用3阶龙格库塔间断伽辽金(RKDG)方法求解,其中空间离散采用基于间断伽辽金(DG)方法,时间离散采用龙格库塔(RK)方法,数值通量采用一阶中心(FORCE)通量,而非线性斜率限制器选取用全变差有界(TVB)检测的von Leer 全变差下降(TVD)限制器(在欧拉方程的特征量上使用),结构的运动方程采用3阶龙格库塔法数值求解,流固耦合基于虚拟流体法,具体的求解过程可以参考Jin等,求解程序基于Fortran编译器编制。

2.1 水下冲击波与浮在自由面平板相互作用

水下冲击波与浮在自由面平板相互作用问题,首先由Bleich等用特征线法求解该问题。由于重力引起水下落过程时间较长,直接研究自由面与冲击波相互作用不利于分析,因此在自由面上悬浮一平板,可以使水中空化溃灭时间提前,其实质特征与冲击波与自由面相互作用类似。水下冲击波与浮在自由面平板相互作用问题示意图,如图3所示。

由于该问题需考虑重力,因此需对水的控制进行修正。考虑重力的水的控制方程为

Ut+F(U)x=S(U)

(9)

其中:

(10)

由于冲击波压力不大,线性化水的状态方程。水下冲击波与浮在自由面平板相互作用问题初始条件取ρ0= 989 kg/m3,c0= 1 451 m/s,p0= 0.101 MPa,g= 9.81 kg m/s2,pmax= 0.71 MPa,θ= 0.995 8 ms,m1= 143.405 kg/m2。计算域取[-10, 0.2]m,网格大小选取10 mm。

水的密度、速度、压力赋值方程为

p(x)=pmaxe-(t-x/c0)/τ+p0+m1g-ρ0gx

u(x)=pmaxe-(t-x/c0)/θ/ρ0c0

(11)

2.1.1 饱和蒸汽压取2 068.5 Pa时不同模型对比

当饱和蒸汽压psat取2 068.5 Pa时,不同空化模型计算空化区域随着时间变化曲线和平板速度时间历程曲线的结果对比如图4所示。从图4(a)可知,空化2.4 ms以前,不同空化模型计算向远处传播的空化并无差别,而在2.4 ms以后,截断模型在空化远端开始向近端方向溃灭,而修正的Schmidt模型与等熵空化流模型的空化则继续向远处传播一定距离后才开始溃灭。修正的Schmidt模型空化传播距离最远,其次为等熵空化流模型。修正的Schmidt模型空化溃灭的速度比等熵空化流模型更快,等熵空化流模型在远端溃灭过程较为平缓。在近结构端为空化溃灭边界,逐渐向远离结构方向移动,修正的Schmidt模型和等熵空化流模型计算结果基本一致,而截断模型溃灭速度较慢,与另外两个模型有一定差别。截断模型空化完全闭合发生的深度小于另外两个模型,发生时刻也晚于另外两个模型。修正的Schmidt模型和等熵空化流模型完全闭合深度与发生时刻基本一致。从图4(b)可知,不同空化模型计算结果对结构速度曲线影响很小,由此可以推断不同空化模型计算的空化闭合载荷的差别对结构响应影响不大。

截断模型、修正的Schmidt模型和等熵空化流模型在饱和蒸汽压取2 068.5 Pa,t= 10.4 ms时刻压力场和速度场计算结果对比如图5所示。根据图4(a)的结果,在t= 10.4 ms时,空化完全溃灭。从图5可以看,截断模型计算的场结果与修正的Schmidt模型、等熵空化流模型相比有显著差异。空化溃灭时刻晚于另外两种模型。而等熵空化流模型与修正的Schmidt模型在靠近结构端也出现细微差异。修正的Schmidt模型溃灭载荷向结构方向传播的距离比等熵空化流模型溃灭载荷向结构方向传播的距离远。而在溃灭点远离结构方向,两种模型计算结果无显著差异。

(a) 压力场

2.1.2 饱和蒸汽压取0.1 Pa时不同模型对比

Bleich和Sandler研究此问题时,将流体假设为双线性水,当流体压力小于零时用零替代。由于修正Schmidt模型和等熵空化流模型需要将饱和蒸汽压设置为正数,否则无法求解,本文取饱和蒸汽压力0.1 Pa。饱和蒸汽压的敏感性分析表明取饱和蒸汽压力0.1 Pa接近饱和蒸汽压取零的结果,可与Bleich和Sandler解析结果对比。

饱和蒸汽压力取0.1 Pa时不同空化模型计算空化区域随着时间变化曲线和板速度时间历程曲线的结果对比,如图6所示。从图6(a)可知,截断模型、修正的Schmidt模型和等熵空化流模型在饱和蒸汽压力取0.1 Pa计算得到空化区域随着时间变化结果无显著差别。参考图4可以推断,不同模型空化区域结果与饱和蒸汽压力取值有很大关联。不同空化模型与解析结果存在一定差别,但差别不大。差别可能来源于初始条件、流体状态方程无法完全一致引起。从图6(b)可知,不同空化模型计算平板速度时间历程曲线结果无显著差别,同时与Bleich和Sandler解析结果也差别不大。与Bleich和Sandler解析结果的对比也可以印证空化模型的正确性。

(a) 空化区域演化

截断模型、修正的Schmidt模型和等熵空化流模型在饱和蒸汽压取0.1 Pa,t= 10.2 ms时刻压力场和速度场计算结果对比如图7所示。根据图6(a)的结果,在t= 10.2 ms时,空化完全溃灭。从图7可知,截断模型、修正的Schmidt模型和等熵空化流模型计算得到的流场结果无显著差别。对比图5也可以推断,不同模型空化区域结果与饱和蒸汽压力取值有很大关联。

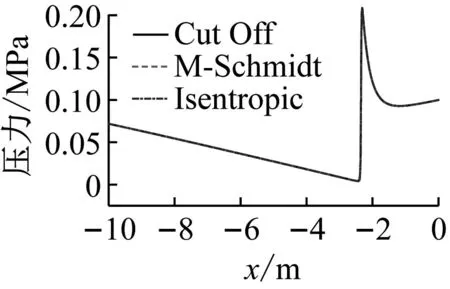
(a) 压力场

2.2 水下冲击波与弹性支撑平板相互作用

图8 水下冲击波与弹性支撑平板相互作用模型示意图

计算域取[-4,0.01]m,网格尺寸0.2 mm,m= 10 kg/m2,ψ= 2.5,κ= 0.2,pmax= 10 MPa, 状态方程中取p0= 0.101 MPa。由于理论结果空化压力取0,因此为了与理论结果对比,取饱和蒸汽压psat= 0.01 Pa。截断模型与Schiffer理论计算结果对比如图9所示。从图9可知,截断模型计算空化区域随着时间变化的无量纲曲线、弹性支撑板湿表面无量纲压力时程曲线以及弹性支撑板无量纲速度时程曲线与Schiffer理论计算结果均较好吻合,说明计算模型的正确性。

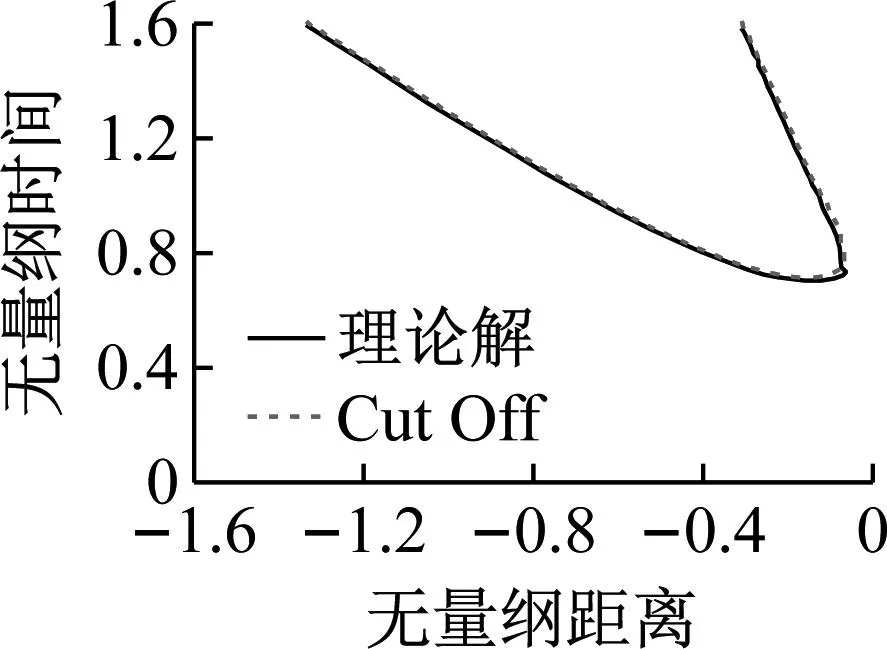
(a) 空化区域演化

2.2.1 输入峰值压力10 MPa不同模型对比

图9为与理论结果对比,取饱和蒸汽压0.01 Pa。为更接近实际结果,下面研究取饱和蒸汽压2 068.5 Pa,对比不同空化模型对空化载荷以及结构响应的影响。取输入峰值压力pmax= 10 MPa。对比截断模型、修正的Schmidt模型和等熵空化流模型计算空化区域随着时间变化无量纲曲线、弹性支撑板湿表面无量纲压力时程曲线以及弹性支撑板无量纲速度时程曲线的结果,如图10所示。计算结果表明在峰值压力pmax= 10 MPa,饱和蒸汽压取2 068.5 Pa时,截断模型、修正的Schmidt模型和等熵空化流模型计算空化区域随着时间变化、湿表面压力、弹性支撑板速度结果并无显著差别。

(a) 空化区域演化

(a) 压力场

2.2.2 输入峰值压力0.3 MPa不同模型对比

当输入峰压pmax= 10 MPa时,不同空化模型计算结果区别较小,这可能由于流体压力相比空化压力较大引起的,下面取输入峰压pmax= 0.3 MPa,空化压力取2 068.5Pa时,开展不同空化模型对比研究。

对比截断模型、修正的Schmidt模型和等熵空化流模型计算空化区域随着时间变化无量纲曲线、弹性支撑板湿表面无量纲压力时程曲线以及弹性支撑板无量纲速度时程曲线的结果,如图12所示。图12(a)计算得到的空化区域随着时间变化无量纲曲线相比图10(a)空化区域显著减小,这是由于入射压力变小,导致结构速度变小,从而引起稀疏波变小,这使得流体更难发生空化,因此空化区域变小。而随着输入峰压降低,可以看到修正的Schmidt模型计算远结构端空化域的传播比截断模型和等熵空化模型计算结果快。而近结构端空化溃灭边界的传播,不同模型计算结果差距不大。从图12(b)和图12(c)可知,即使输入峰压取0.3 MPa,不同模型计算湿表面压力和板速度结果差别很小。

(a) 空化区域演化

(a) 压力场

2.3 水下冲击波与水背衬平板相互作用

水下冲击波与水背衬平板相互作用问题,Schiffer等通过试验方法开展过相关研究。通过该问题的分析,可以深化不同空化模型对由于水背衬结构运动而产生的局部空化的影响的认识。水下冲击波与水背衬平板相互作用模型示意图如图14所示。为了与Schiffer试验结果对比,取流体密度ρw= 1 000 kg/m3, 流体声速cw= 1 053 m/s,计算域[-4,2]m,网格尺寸0.5 mm,m= 111.1 kg/m2,ψ= 0.91,pmax= 15.1 MPa,θ= 0.096 ms, 状态方程中取p0= 0.101 MPa。空化压力取2 068.5Pa计算结果与Schiffer试验结果对比,如图15所示。从图15可知,空化边界和溃灭边界的计算结果与试验结果吻合较好。出现的误差可能是来自观测误差以及平面波假设不完全(试验中透明管子直径为27 mm)。

图14 水下冲击波与水背衬平板相互作用模型示意图

图15 水下冲击波与水背衬平板相互作用问题试验和截断

三种空化模型分别计算空化区域、面板前压力、面板后压力和面板速度随时间变化的结果对比,如图16所示。从图16(a)可知,空化边界在t= 0.85 ms以后不同模型出现了不同曲线,修正的Schmidt模型继续以原来的传播速度向远处传播,等熵空化流模型则以相对缓慢的速度继续向远处传播,而截断模型则向结构端方向溃灭,近结构端的溃灭边界三种模型并无差别。这可能由于数值误差引起的。由于间断波在传播过程中,通常在间断波前存在较小的波动,当远端压力低到与间断波前的波动量级接近时,会表现出较大数值误差,而空化区域对极小的波动敏感,从而影响图16(a)中的曲线。图16(a)中在远端的空化区域可能会因为数值求解格式、数值通量、求解格式精度等因素不同而存在差别。但实际上这对结构和流体整体响应结果影响极小。从图16(b)、图16(c)和图16(d)三种模型计算结构响应结果并无差别。

(a) 空化区域演化

水下冲击波与水背衬平板相互作用问题在t= 1.5 ms时刻不同空化模型计算压力场和速度场结果,如图17所示。在t= 1.5 ms时刻,参考图16(a),在冲击波后,空化发生后,扩展到较大规模,且三种模型计算远端的空化边界具有很大不同。空化内流体速度仍朝向结构方向。并且越靠近结构空化区域的流体速度越大。从图17可知,不同空化模型计算压力场和速度场在空化区域附近无明显差别。

(a) 压力场

虽然图16(a)计算的远端的空化边界存在差别,但在场计算时并无显著体现,说明图16(a)中不同空化模型计算结果的差别可能来自不同模型的数值误差,空化区域不同的差别并不会引起场结果及结构响应的显著差别。

3 结 论

本文建立了空化截断、修正的Schmidt和等熵空化流三种空化模型,并将其结合在龙格库塔间断伽辽金数值框架下。开展三种不同空化模型应用在水下冲击波与浮在自由面平板相互作用问题,水下冲击波与弹性支撑平板相互作用问题及水下冲击波与水背衬平板相互作用问题的对比研究。研究结果表明:

(1) 当计算压力小于饱和蒸汽压时,截断模型的压力保持在饱和蒸汽压,而修正的Schmidt模型和等熵空化流模型随着密度降低压力迅速下降。修正的Schmidt模型在较小的密度变化条件下,下降得更加迅速,而等熵空化流模型表现出较为平滑的曲线。在压力小于饱和蒸汽压且大于修正Schmidt模型的截断压力pε时,相同密度条件下,修正的Schmidt模型获得的压力小于等熵空化流模型。

(2) 当流体环境压力较大时,由于饱和蒸汽压远远小于流体压力,因此,不同空化模型的差别难以对整体计算结果起到显著影响。当流体环境压力不大,接近大气压时,截断模型计算的密度结果在空化中心处略大于修正的Schmidt模型和等熵空化流模型的结果,不同空化模型计算的压力结果在流体压力下降到空化压力之后产生差别。截断模型的压力保持为恒定的压力,修正的Schmidt模型在稀疏波过后压力即快速下降,而等熵空化流模型在低压区域比修正的Schmidt模型更小。总体来讲,修正的Schmidt模型与等熵空化流模型计算结果差别很小,而截断模型与另外两个模型计算结果在空化区域附近略有差别,但并不显著。

(3) 影响不同空化模型计算结果的主要因素包括饱和蒸汽压和峰值压力。当饱和蒸汽压很小,不同空化模型计算结果差别很小。

(4) 当饱和蒸汽压较大且峰值压力很大时,不同空化模型计算结构响应差别很小,而空化区域演化会由于时间步长较多时累积的数值误差出现差别。对于水背衬空化边界,修正的Schmidt模型继续以原来的传播速度向远处传播,等熵空化流模型则以相对缓慢的速度继续向远处传播,而截断模型则向结构端方向溃灭,近结构端的溃灭边界三种模型并无差别。

(5) 当饱和蒸汽压较大且峰值压力很小时,不同空化模型计算结构响应差别很小,而空化区域演化和场输出结果可能会由于数值误差出现差别。修正的Schmidt模型计算远结构端空化域的传播以及靠近结构的溃灭边界向远处传播速度比截断模型和等熵空化模型计算结果快。