基于超图相关距离判别投影的轴承故障诊断方法

2023-12-18苏树智张志鹏

振动与冲击 2023年23期

苏树智, 张志鹏

(安徽理工大学计算机科学与工程学院,安徽淮南 232001)

滚动轴承是重要的机械基础件,被广泛应用于机械制造、工业生产等重要领域。一旦轴承发生故障往往会造成重大的经济损失,甚至威胁人身安全[1-2]。因此,针对滚动轴承的故障诊断技术具有重要的现实意义。

故障特征的提取是故障诊断的关键。滚动轴承故障特征的提取和轴承故障分类的准确性是轴承故障诊断领域的重要课题之一。其中,基于振动信号分析[3-5]的方法已经成为了目前故障诊断的关键手段之一。为了获取更加丰富的故障信息,一般需要从多角度提取振动信号的统计特征参数,这使得故障数据间变的更加冗余,导致故障分类困难,难以提取更加有效的故障特征。因此,良好的降维方法是提取易于辨识故障类别特征的关键。

流形学习[6]作为有效的数据降维方法,能够保持故障数据的局部近邻关系,更好地揭示高维故障数据的流形特征。Roweis等[7]提出了局部线性嵌入(locally linear embedding,LLE)算法,是一种基于图的无监督非线性降维方法,通过求解特征值问题来计算每个点的重构权值,并使嵌入最小化。Wang等[8]对LLE进行改进,提出了一种基于统计的局部线性嵌入(statistical locally linear embedding,SLLE)的降维算法,利用故障类别的标签信息对局部嵌入算法进行扩展,考虑了数据的局部几何结构和类信息。Li等[9]提出拉普拉斯特征映射(Laplacian eigenmaps,LE)算法,通过构建图相似矩阵来重构数据流形的局部结构特征,在低位空间中能够尽可能的保留局部样本间的结构关系。梁超等[10]提出了局部保持投影(locality preserving projections,LPP)算法,LPP是一种被视为替代主成分分析[11]的线性降维方法,通过构造数据局部结构的投影矩阵,保留了隐藏在训练集中的非线性子流形结构和数据的局部邻域信息。Zang等[12]提出了弹性保持投影(elastic preserving projections,EPPs)算法。EPPs继承了LPP和NPE[13](neighborhood preserving embedding)等局部降维方法的优点,结合了数据的局部几何特性和全局信息,能够发现隐藏在训练集中的非线性子流形结构。

流形学习方法一般通过简单二元图描述样本空间结构关系。然而,实际问题中的轴承故障数据通常嵌入在高维空间中,每个数据样本之间的关系较为复杂,简单无向图使用二元关系来描述样本间联系的方法,无法探究数据复杂的高阶关系。并且,流形中经常采用欧氏距离度量故障样本间的权值与近邻。但流形中样本点距离为测地距离,不是简单的两点之间的直线距离。在高维流形中,用欧氏距离来表示数据的图结构不仅容易受到数据噪声的影响,而且欧氏距离对数据的范围取值较敏感,无法准确揭示数据的内在结构关系。

为了解决上述问题,提出采用超图结构[14]描述不同轴承故障样本间的结构关系,利用轴承故障样本的监督信息构建出类内超图和类间超图。超图结构有效挖掘故障数据本身的复杂多重结构,在表达样本间的多元关系的同时更好的揭示了不同故障类型的内在性质。并且在超图中通过皮尔森相关系数[15]与欧氏距离融合的新度量(相关距离)来计算高维流形中样本间的测地距离,避免了欧氏距离受故障数据取值范围敏感导致的分类不准确问题。超图相关距离判别投影方法更好的挖掘了不同轴承故障样本的多元结构关系,提高了故障分离的准确性。

1 相关性及图学习基础理论

1.1 相关性理论

皮尔森相关系数是一种经典统计学方法,可以通过计算两个向量之间的相关性系数来衡量两者之间的相似性程度。相关系数作为反应变量间相似性程度的统计量,通过计算特征和类别间的相似度来判断其相关程度。

皮尔森相关系数一般使用相关系数ρ表示,ρ∈[-1,1]。

定义1给定两个变量x∈Rn和y∈Rn,它们之间的皮尔森相关系数为

(1)

式中:E(x)和E(y)分别为变量x和y的期望;D(x)和D(y)分别为变量x和y的方差。

1.2 图学习

图可以直观地描述成对故障样本之间的关系,揭示数据之间的几何性质。传统的简单图,如图1所示。每条边连接两个不同的顶点,通过赋予该边一定大小的权重来衡量两样本之间的关联性。

图1 简单图

对于一个简单两向图,一般表示为

G={X,E,W}

(2)

式中:X为样本的顶点集;E为顶点间的边集;W为顶点之间边的权重矩阵。

简单两向图一般采用相似性度量的方法来定义两顶点之间连通的边和其对应的权值。如果顶点i,j相似,则在顶点i,j之间定义一条边和它的相似权值。

2 超图相关距离判别投影

2.1 相关距离的构建

在高维空间中,欧式距离往往无法真实的反应故障样本之间相对位置关系,无法通过计算的测地距离选取合适的近邻样本点,使后续算法无法准确对轴承故障进行准确分类。

欧氏距离对变量的取值范围较为敏感,在面对复杂工况的高维轴承故障信号时,度量更容易失效,进而难以反应出高维故障数据间的真实结构。皮尔森相关系数反映的是样本间的相似性程度,不受样本维度和取值的影响,在高维空间中能够准确反应故障特征和类别的相似性关系。对此,本文定义了一种新的度量方法——相关距离。新度量在欧氏距离的基础上通过相似性度量了高维空间中样本点的相似性关系。

定义2给定两个变量xi∈Rn和xj∈Rn,它们之间的相关距离为

(3)

皮尔森相关系数和欧式距离融合后的新度量在一定程度上解决了流形中单一依赖欧式距离导致的度量不准确的问题。新度量不仅避免了欧氏距离对变量范围的取值敏感和在高维流形中度量不准确的问题,也为相似性权值矩阵的鲁棒性创造一定的基础。

为了验证相关距离的优势,在西储大学轴承数据集上计算了样本距离。相关距离的同类距离均值明显增加,异类距离均值小幅度变化,如表1所示。所以,相关距离能够有效的提高不同轴承故障间的可分离性。

表1 不同度量方式的距离比较

2.2 超图结构

不同于简单图结构每条边只能连接两个顶点,超图如图2所示。从图2可知,一条超边可以连接的顶点是不受限制的。

图2 超图

对于一个超图,它的一般表示为

GH={V,EH,WH}

(4)

超图中,关联矩阵H=|V|×|E|来表示顶点和超边的关系。关联矩阵H描述了图2中超图顶点vi和超边ej的关系,如表2所示。其定义如下

表2 超图关联矩阵H

(5)

超图中顶点的度为包含该顶点的所有超边的权重和,超边的度为该边内包含的顶点个数。顶点的度d(v)和超边的度δ(e)定义如下

(6)

(7)

超图相对简单图能够涵盖更丰富的空间结构信息。广义的边可由多个顶点构成,每个顶点可以在多个超边中,能够描述复杂的轴承故障样本多元关系。

2.3 HCDDP(hypergraph correlation distance discriminant projection)算法设计

HCDDP通过超图这种新的图结构来描述不同轴承故障信号间的流形结构关系。并利用轴承故障信号的监督信息构造了类内超图和类间超图。在超图的构建中,使用相关距离来度量流形空间中故障样本的测地距离。

2.3.1 类内超图的构建

根据样本的类别信息,通过类内样本近邻关系构建类内超图GHw

GHw={V,EHw,Ww}

(8)

式中,EHw和Ww为通过类内近邻样本点构建的类内超边和类内超边权重。通过近邻算法选择k个近邻点来构建类内关联矩阵Hw。

类内关联矩阵Hw的定义为

(9)

式中:Nkw(x)为与x同类的k个近邻点;l(x)为x的标签信息。

类内超边ew的权重通过相关距离进行构建

(10)

式中:wi,w构建类内超图中的权重矩阵Ww,Ww=diag([w1,w,w2,w,…,wn,w])为一个对角矩阵。

类内超图顶点的度di,vw和超边的度dj,ew可以表示为

(11)

(12)

在低维空间中,通过最小化类内距离,构建以下的目标函数

(13)

即,类内样本目标函数为

minATXLwXTA

(14)

式中:Lw=Dvw-HwWw(Dew)-1(Hw)T为类内超图拉普拉斯矩阵;Dvw为类内顶点的度矩阵;Hw为类内点边关系矩阵;Ww为类内超边的权重矩阵;Dew为类内超边的度矩阵。

2.3.2 类间超图的构建

类间超图根据样本的标签数据和类间样本近邻关系,表示如下:

GHb={V,EHb,Wb}

(15)

式中:EHb和Wb为通过类间近邻构建的类间超边和类间超边权重。同样使用近邻算法选择k个近邻点来构建类间关联矩阵Hb。

类间关联矩阵Hb如下式计算得到

(16)

式中:Nkb(x)为与x不同类的k个近邻点;l(x)为x的标签信息。

类间超边eb的权重wi,b也通过相关距离来计算,wi,b由下式计算得到

(17)

类间超图中,顶点的度和超边的度有如下表示

(18)

(19)

在低维空间中,通过最大化类间距离,构建了类间超图的目标函数

(20)

即,类间样本目标函数为

maxATXLbXTA

(21)

式中:Lb=Dvb-HbWb(Deb)-1(Hb)T为类间超图拉普拉斯矩阵;Dvw为类间顶点的度矩阵;Hw为类间点边关系矩阵;Ww为类间超边的权重矩阵;Dew为类间超边的度矩阵。

2.4 构建HCDDP优化模型

HCDDP使用新的度量方法重构了超图中的权重矩阵W。考虑了不同样本之间复杂的多元关系,对故障样本的类内超图和类间超图进行构造,使在低维空间中提高不同类别样本的可分性。

HCDDP被表示为如下的两个优化函数

(22)

为了避免无用解,给出以下限制条件

(23)

通过构建最小化类内函数和最大化类间函数,给出HCDDP的优化模型

(24)

式中:L=Lb-Lw;D=Dvb-Dvw。

根据代数和矩阵相关知识,通过求解式(25)得到的最优特征向量使优化模型最大化

XLXTα=λXDXTα

(25)

HCDDP算法的基本过程,如表3所示。

表3 HCDDP算法过程

HCDDP利用相似距离构建了超图中的邻接矩阵HW(De)-1HT。在考虑样本在高维流形中的空间几何结构的同时,通过超图构建了类内最小化和类间最大化的优化函数。超图结构准确描述了具有多元关系的故障样本,有效减少样本不平衡带来的问题。

3 基于HCDDP的轴承故障诊断方法

本文提出了一种基于HCDDP的轴承故障诊断方法,类内类间判别超图结构在去除高维故障数据冗余信息的同时,增强了样本间的高阶关联能力,并在超图中利用相关距离构建了权重矩阵,准确揭示了不同样本的相似性关系。

轴承故障振动信号中不同的故障类别有着不同的表征,这些表征往往存在于信号的各个特征中。本文试验中对轴承振动信号的时域、频域和时频域进行提取28种相关特征[16-17],如表4所示。表4中:1～16的时域特征中1～9为有量纲指标,能够直观反应信号的物理含义;10～16为无量纲指标,不易受噪声的影响;17～20为信号的频域特征;21～28为信号的时频域特征。本文试验中,为了消除数据特征之间的量纲影响,对多域特征进行了归一化处理。多域特征的结合能够丰富故障特征种类,增强故障判别能力。

表4 特征参数

基于HCDDP的轴承故障诊断方法实现过程主要为以下几个步骤:

步骤1:通过对传感器采集到的原始时域信号转化成多域的高维故障数据集来提取特征参数,并划分为训练样本数据集和测试样本数据集两部分。

步骤2:将训练样本数据集输入到基于类内超图和和类间超图目标函数构建的HCDDP模型中进行训练,从而得到投影矩阵。再利用投影矩阵对测试样本集进行维数约简得到低维的特征集。

步骤3:最后将低维特征集输入到SVM分类器中训练。通过训练好的分类模型进行故障分类,完成轴承故障的诊断。

流程图如图3所示。图3中,n为故障类别数。

图3 基于HCDDP的轴承故障诊断流程图

4 试验结果与分析

为验证本方法的可行性和准确性,建立的故障诊断方法分别在西安交通大学滚动轴承数据集[18](Xi’an Jiaotong University-Changxing Sumyoung Technology Co., Ltd., XJTU-SY)和美国凯斯西储大学轴承数据集(Case Western Reserve University, CWRU)上进行了试验。

4.1 在XJTU-SY轴承数据集上的试验

该轴承数据集来自西安交通大学轴承数据集,试验轴承为LDK UER204滚动轴承,如表5所示。

表5 LDK UER204轴承参数

本试验采用的是PCB 352C33单向加速度传感器在测试轴承的竖直方向采集到的振动信号,试验台如图4所示。采样频率为25.6 kHz,采样间隔为1 min,每次采样时长为1.28 s。本试验选取了工况2中的Bearing2_1(内圈失效)、Bearing2_2(外圈失效)和Bearing2_3(保持架失效)三个数据集。将振动信号以1 024为采样长度划分样本,随机试验重复十次,选取10次的均值为试验的识别率。

图4 轴承试验台

为验证HCDDP维数约减的有效性,每类样本200个,随机设置100组为训练集,剩余100组为测试集。PCA(主成分分析)、KPCA(核主成分分析)、LLE(线性判别嵌入)、OEPP(正交弹性保持投影)和KEPP(核弹性保持投影)分别在该数据集上进行试验,邻域参数设置为KLLE=5,KOEPP=5,KHCDDP=5,其中KPCA核参数设置为2。

将得到的低维特征子集输入到SVM(suppot vector machine)分类器中进行了故障分类。得到了不同方法在该数据集上的平均故障识别率,如表6所示。标准差反应了识别率的波动情况。

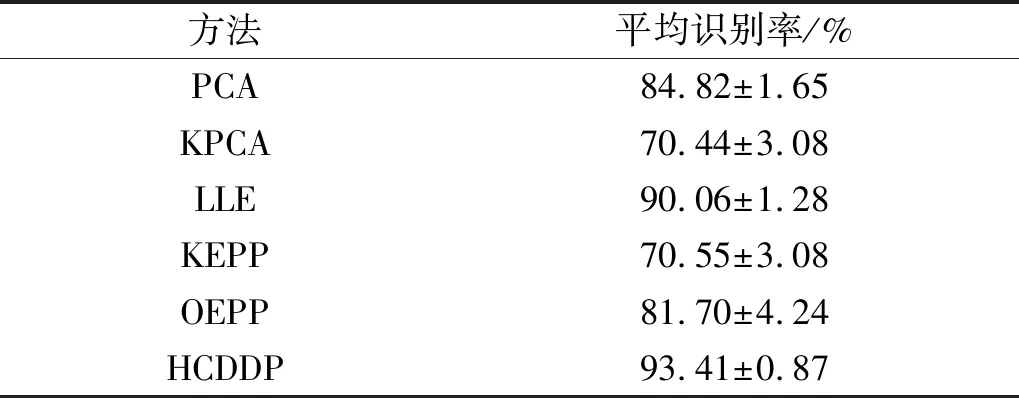
表6 不同方法的平均故障识别率

表6中,KPCA对轴承故障分类效果较差,核函数的方法在面对复杂非线性故障样本时无法很好的处理。PCA只考虑了数据的全局信息,对故障数据的特征利用不够充分,平均识别率一般。OEPP和KEPP两者都是无监督算法,无法很好利用样本的标签信息,表现均不HCDDP。LLE利用局部线性关系反应全局信息,识别效果良好。而HCDDP使用相关距离超图构建的类内和类间样本关系,能够更好的揭示样本之间的多元关系和准确度量样本之间的距离,有着更高的平均准确率。

为了进一步验证方法的有效性和稳定性,通过逐步增加训练集的数量来观察准确率的变化曲线。每类随机样本的个数分别设置10,20,30,40,…,190,200,识别率如图5所示。

图5 故障识别率随样本个数变化曲线

从图5可知,OEPP在随着训练样本逐渐增加的过程中,平均识别率有较大的波动,且平均识别率不高。KPCA和KEPP随着训练样本的增加,整体平均识别率较为稳定,但未有较大提升。PCA随着训练样本增加,平均识别率增长稳定,始终高于KEPP和KPCA。LLE初始平均识别率较高,但随着训练样本的增加,没有保持较大幅度的提升。本文提出的HCDDP算法能够在训练样本逐渐增加的同时保持平均识别率的稳定增长,并且维持较高的识别率。

4.2 在CWRU轴承数据集上的试验

该数据集来自美国凯斯西储大学的轴承故障数据集。轴承类型为深沟球轴承,参数如表7所示。

表7 轴承规格

实验台如图6所示。电机驱动端加速度传感器采集到的无故障、内圈故障、滚动体故障和外圈故障的振动信号,如图7所示。

图6 CWRU轴承试验平台

图7 4种轴承振动信号

本试验选取凯斯西储大学轴承数据集中采样频率为12 kHz,损伤直径为0.177 8 mm的驱动端数据集。将振动信号以1 024为采样长度划分一个样本,每类故障数据均为110个样本,从中随机选取50个作为训练样本,剩余60个作为测试样本。为了避免实验的偶然性,随机试验重复10次,取10次均值作为最终识别率。

为验证HCDDP维数约简的有效性,使用KPCA、LLE、OEPP三种算法进行了对比试验。将轴承数据集分别通过KPCA、LLE、OEPP降到三维,使用三维特征分布图来直接展示降维效果。其中,邻域参数分别设置为KLLE=5,KOEPP=5,KHCDDP=5,其中KPCA核参数设置为2。

图8(a)、图8(b)、图8(c)、图8(d)分别为与测试数据集进行维数约简后的三维特征分布图。图8(a)中通过KPCA降维后内圈故障样本和滚动体故障样本混叠明显,外圈故障样本和正常样本的类内聚类的效果一般,不能准确区分出各类的故障类别。图8(b)中OEPP的降维后类间样本间距较近,样本混叠明显,无法很好的区分不同故障类型。图8(c)中LLE在三维特征分布中各类轴承故障分类效果较为明显,但类内聚集性不明显,类间分类界限模糊。相对以上三种算法,HCDDP在三维特征分布图中样本类间分类界限明显,聚类效果良好,能够准确的区分不同的故障类型。

(a) KPCA

为了进一步验证HCDDP算法在该数据集上的有效性,将基于PCA、KPCA、LLE、KEPP、OEPP和HCDDP六种方法得到的低维特征子集输入到SVM分类器中进行轴承故障分类。训练样本50,测试样本60下不同方法的平均故障识别率,标准差反应了识别率的波动情况,如表8所示。

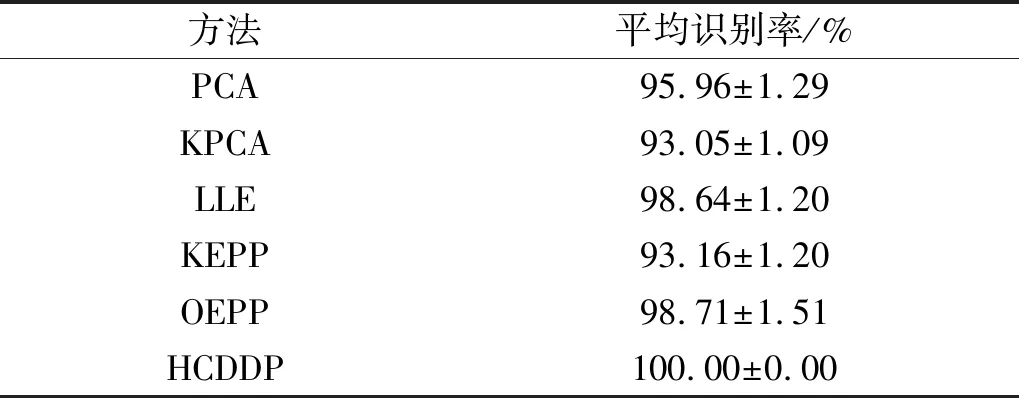
表8 不同方法的平均故障识别率

由表8可知,非线性降维算法KPCA和线性降维算法PCA都只考虑了样本的全局信息,在本轴承数据集上的表现一般。LLE平均识别率良好,但不及OEPP。KEPP和OEPP都利用了样本的局部和全局信息,对该数据集的识别率较好,但平均识别率的波动较大,相比HCDDP,无法稳定的保持较高的平均识别率。

鉴于轴承工作环境较为复杂,不同工况下轴承产生的故障特征不同,故障诊断算法在单一工况下无法测试其泛化能力。为了更加全面的验证基于HCDDP故障诊断方法的泛化性,针不同工况下的同一故障进行故障诊断,分别使用转速为1 730 r/min、1 750 r/min、1 772 r/min、以1 797 r/min下的四种工况数据进行了故障识别率实验。为了观察故障识别率随着训练样本增加的变化曲线,将每类随机训练样本数量分别设置为10,20,30,…,100,110,进行试验,结果如图9所示。六种算法在不同工况下训练样本为10,20,…,100,110时的十次平均识别率的实验,综合衡量了算法在不同训练样本数量下的平均识别率,如表9所示。

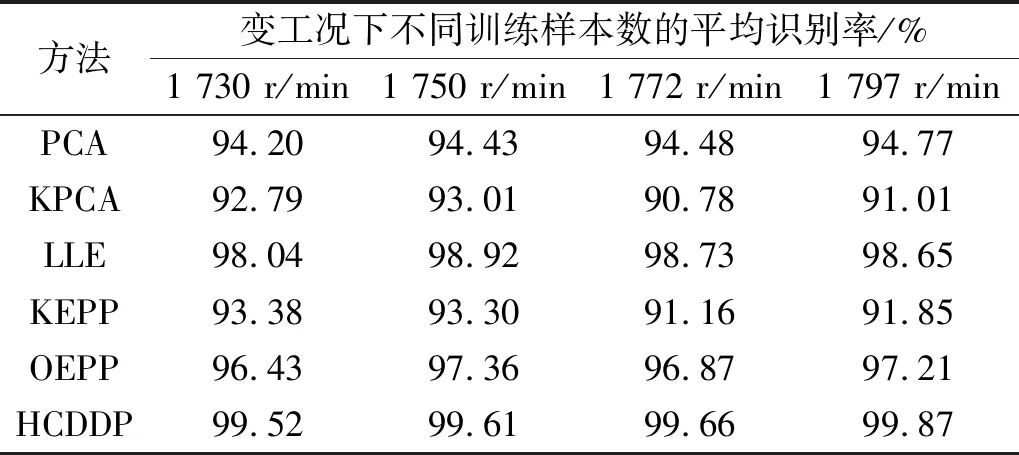
表9 多工况下不同训练样本数的平均故障识别率

(a) 1 730 r/min下故障平均识别率

通过上述六种算法在表9和图9中的数据可知HCDDP在四种工况下表现良好,识别率较稳定,高于LLE。PCA、KPCA以及KEPP在各种工况下当训练样本较少时准确率偏低,且整体表现不稳定。OEPP整体表现较为良好。在1 750 r/min工况下和HCDDP最接近,但OEPP在不同工况下的适应能力弱,在1 730 r/min和1 797 r/min这两种工况下。训练样本较少时准确率较低,随着训练样本的增加准确率也没有保持较平稳的增长。

综上,HCDDP在各工况下不同训练数量时平均识别率均表现较好,在训练样本较少时依然有着较高的故障识别率。判别超图结构在训练样本增加时进一步丰富了样本间的多元结构关系,保持了平稳的故障识别率。