基于易损性的大跨度斜拉桥黏滞阻尼器参数优化

2023-12-18李立峰李名华

振动与冲击 2023年23期

李立峰, 李名华, 胡睿

(1.湖南大学土木工程学院,长沙 410082;2.湖南大学风工程与桥梁工程湖南省重点实验室,长沙 410082)

斜拉桥的主要构件包括斜拉索、主梁、桥塔、边墩和支座等,因其跨越能力强、施工简便而广泛使用。斜拉桥桥塔的损伤破坏会影响桥梁的整体受力,因此大跨度斜拉桥多采用塔梁分离体系以保证桥塔始终处于弹性受力状态。塔梁分离体系的主梁易产生较大的纵向位移,大跨度斜拉桥通常会采用黏滞阻尼器以控制主梁位移。黏滞阻尼器由于提升了斜拉桥的耗能性能,故可在不增大桥塔内力的情况下控制主梁的纵向位移。

黏滞阻尼器的减震效果取决于参数设计,因而阻尼器的参数优化是斜拉桥抗震设计的关键。已有许多学者进行了斜拉桥减隔震装置的参数分析和优化。焦驰宇等[1]研究了弹性索刚度和黏滞阻尼器参数对斜拉桥地震响应的影响,评价了不同塔梁连接方式的减震效果。胡思聪等[2]研究了常用减震装置在高墩多塔斜拉桥中的减震效果,并从传力机理的角度解释不同布置形式下控制参数对减震效果的影响规律。刘彦辉等[3]分析了黏滞阻尼器对全漂浮大跨斜拉桥的减震效果,研究发现在固定速度指数下,主塔弯矩和塔梁位移随阻尼指数单调递减。黄民水等[4]对独塔斜拉桥的黏滞阻尼器进行了参数分析,研究发现速度指数和阻尼系数对关键节点位移和截面内力的影响呈相反趋势。黎璟等[5]分析了不同设防烈度下铁路斜拉桥减震装置的参数优化方法,研究发现减震效率与设计参数的关系并非单调变化。尽管许多研究探讨了不同减隔震装置参数对斜拉桥地震响应的影响,但参数分析结果仍无法直接运用于优化设计。为此,孙传智等[6]提出了基于响应面法的减震结构黏滞阻尼器参数优化方法,通过参数优化模型兼顾了结构和阻尼器的受力要求。王波等[7]为考虑地震动随机性对黏滞阻尼器参数优化的影响,采用虚拟激励法简化了斜拉桥的非线性时程分析,再结合响应面法进行参数优化。以上学者在参数分析基础上,通过响应面法建立了设计参数与地震响应的关系,再利用优化算法求解最优参数。然而该方法通常只能考虑单一构件的极限能力,无法考虑构件间的相对损伤情况,最优参数下的损伤路径可能并不合理。此外,该方法的优化结果依赖于选取的地震波,未能充分考虑地震动随机性的影响。

针对以上问题,本文提出了基于易损性和响应面的优化方法:采用易损性理论评估不同黏滞阻尼器参数下的构件及系统抗震性能,利用响应面法拟合黏滞阻尼器参数与构件及系统抗震性能的非线性函数关系,以系统损伤概率最小、损伤路径合理为目标进行参数优化。本文的优化思路一方面采用易损性分析理论考虑地震波随机性的影响;另一方面,系统易损性可作为反映斜拉桥整体抗震性能的指标,而构件易损性可用于评估构件间的相对损伤情况,以明确构件的损伤路径。

1 依托工程及有限元模型

1.1 工程背景

本文算例为一座50 m+95 m+350 m+95 m+50 m的双塔双索面半飘浮体系斜拉桥,桥梁总体布置情况如图 1(a)所示。主梁采用钢-混组合梁,桥面宽37 m,梁高3.4 m,沿纵向每间隔4 m设一道横梁,梁中心线及两侧设有工字形小纵梁,截面形式如图1(b)所示。索塔为钻石型索塔,塔高125.8 m,主要构造如图1(c)所示。塔、墩基础均采用钻孔灌注桩。桥塔、辅助墩和过渡墩均设有纵横向可活动的球型钢支座;每个桥塔位置沿纵桥向设4个黏滞阻尼器,共计8个;所有塔、墩横向处均设有E型钢阻尼器,共计12个,支座布置如图2所示。

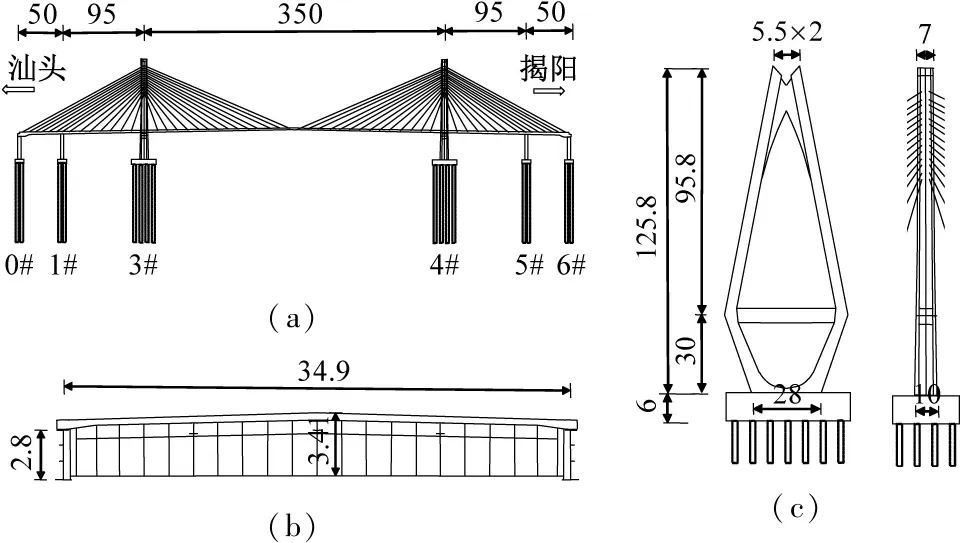
图1 桥梁总体布置及构造形式(m)

图2 支座及减隔震装置布置图

1.2 有限元模型

根据桥梁结构布置并考虑相邻联的影响,建立OpenSees非线性动力模型。采用弹性梁柱单元模拟主梁,引桥质量集中到主梁梁端以考虑相邻联的影响。采用弹塑性梁柱单元模拟塔墩的塑性铰区域,截面为自定义纤维截面;采用弹性梁柱单元模拟剩余区域。采用桁架单元模拟斜拉索,通过刚臂连接斜拉索和主梁。球型钢支座、钢阻尼器和黏滞阻尼器均采用零长度单元模拟,并选择相应的材料模拟支座的约束特性。考虑依托工程主要为混凝土结构,阻尼比取0.03。有限元模型动力特性分析结果如表1所示。一阶纵飘振型如图3所示。

表1 典型振型

图3 一阶纵飘振型(f=0.161 Hz)

2 易损性分析

2.1 理论介绍

结构地震易损性表示不同地震动水平下,结构发生各种损伤破坏的概率,可按式(1)表示

Pf=P[SD≥SC|LS|IM=x]

(1)

式中:Pf为失效概率;IM为地震动强度指标;x为地震动强度水平;SD为结构工程需求参数;SC|LS为结构在特定损伤状态下的抗震能力。

以往研究的地震易损性函数常采用两参数对数正态累计分布函数[8-9]

(2)

(3)

(4)

式(4)为反映工程需求参数和地震动强度水平关系的概率性地震需求模型(probabilistic seismic demand model,PSDM),该模型与离散数据点的离散程度可由对数标准差表示

(5)

式中:SDi为第i条地震波下构件的工程需求参数;N为地震波的数量。

因此,式(2)可表示为

(6)

2.2 损伤状态定义

定义桥梁在不同损伤状态下的损伤指标是易损性分析的重要环节。易损性分析通常将结构的损伤状态划分为:无损伤、轻微损伤、中等损伤、严重损伤和完全损伤五个等级[11]。斜拉桥的抗震薄弱构件包括桥墩、桥塔和支座,同时考虑斜拉桥的自身特点,本文参考相关文献定义了斜拉索、桥墩、桥塔和支座四类关键构件的损伤指标,如表2所示。

表2 不同构件的损伤指标

2.3 地震波选择

为考虑地震波库的随机性,根据震级和震中距定义四类地震波库[12]:SMSR、LMSR、SMLR、LMLR。本文从PEER强震数据库中为每类地震波库选择25条地震波。为确保所选地震波的平均反应谱与设计反应谱一致,分别对四类地震波进行不同程度的调幅,调幅系数分别为2、1、3和2。黏滞阻尼器主要影响斜拉桥的纵向受力,为此仅考虑纵向和竖向地震动输入工况。

2.4 地震动强度指标选择

本文将常用的地震动强度指标分为3类:地震动峰值指标(PGA、PGV、PGD)、反应谱峰值指标(PSA、PSV、PSD)和反应谱指标(SAT1、SVT1、SDT1)。针对以上9种地震动强度指标,本文从效率性、可行性和适用性3个标准评价其在大跨度斜拉桥易损性分析中的优劣[16]。效率性指地震动强度水平下工程需求参数的随机性,用对数标准差βD表示;可行性指地震动强度指标和工程需求参数的关联程度,用回归系数b表示。适用性(ζ=βD/b)综合考虑了效率性和可行性。地震动强波指标评价如图4所示。

(a) 效率性评价

由图4可知:在桥塔、过渡墩、辅助墩支座、过渡墩支座和桥塔支座的结构响应方面,地震动强度指标PGD的效率性(0.208 9～0.769 4)、可行性(0.130 7～1.440 2)和适用性(0.525 7～1.598 3)最好;PGD能有效地预测斜拉索的结构响应(βD=0.208 9),但敏感程度相对较低(b=0.130 7),导致适用性不佳(ζ=1.598 3)。而拉索和辅助墩的最佳地震动指标分别为反应谱峰值指标PSV和地震动峰值指标PGA,次之是地震动峰值指标PGD。综上分析,大跨度斜拉桥易损性分析宜采用地震动峰值指标PGD。

2.5 非减震结构的抗震性能评估

2.5.1 易损性分析

本节采用易损性分析评估非减震结构的抗震性能。在易损性分析中,首先根据云图法构建PSDM;然后建立不同损伤状态下的构件易损性曲线;最后采用一阶上下限算法和PCM算法建立斜拉桥的系统易损性曲线。

对构件峰值地震响应和地震动强度指标进行线性回归可得概率地震需求模型。各构件的概率需求模型回归参数,如表3所示。

表3 各构件的概率需求模型

非减震结构的构件和系统易损性曲线,如图5、图6所示。由图5可知:构件的损伤概率随损伤程度的增加逐渐减小,其中塔、墩损伤概率的下降最为显著。从轻微损伤到严重损伤,支座的最大损伤概率平均下降了31.4%,过渡墩的最大损伤概率下降了73.3%,而辅助墩、桥塔的最大损伤概率分别从78.2%、52.9%下降到不足1%。在不同损伤状态下,塔墩的抗震能力存在显著差异,较低损伤程度下的抗震性能表现较差。支座的损伤顺序在不同损伤状态下保持一致:过渡墩支座的纵向位移最大,其最易损伤,而桥塔支座的纵向位移最小,其最不易损伤。相较于轻微损伤,严重损伤下各支座的最大损伤概率分别下降了22.6%、37.3%、34.4%,损伤概率的变化量较为接近,表明各支座的损伤程度具备一定相关性。

(a) 轻微损伤

由图6可知:随着损伤程度的增加,一阶界限法所得上下界的界限宽度在不断增加,因此本文拟采用PCM算法以避免过大的误差。在严重损伤状态下,PCM算法所得系统易损性曲线更贴近一阶界限的下界,表明损伤越严重,斜拉桥各构件间的损伤相关性越强,单个构件的损伤对系统损伤影响越大。

2.5.2 抗震性能评估

采用PGDsl,0.5表示斜拉桥系统及构件失效概率达到50%对应的地震动峰值位移。PGDsl,0.5越大说明结构发生相同失效概率的地震动强度水平越高、结构的抗震性能越好。轻微损伤状态下系统及构件的PGDsl,0.5,如表4所示。由表4可知,虽然桥塔的PGDsl,0.5达到103.0 cm,但由于过渡墩、过渡墩支座的PGDsl,0.5仅有32.2 cm、33.8 cm,导致斜拉桥的系统PGDsl,0.5只达到24.4 cm。由于斜拉桥的系统抗震性能主要受限于过渡墩和支座的抗震性能,可通过提升其抗震性能以改善系统抗震性能。此外,非减震结构的损伤顺序为:过渡墩、过渡墩支座、辅助墩支座、桥塔支座、桥塔、斜拉索,墩柱先于支座和拉索破坏,结构损伤路径不合理。

表4 非减震结构的系统及构件PGDsl,0.5

为提升系统抗震性能并优化损伤路径,本文采用响应面法探讨黏滞阻尼器参数对斜拉桥系统及构件抗震性能的影响,并通过参数优化确定最优阻尼器参数。

3 黏滞阻尼器的参数优化

3.1 黏滞阻尼器介绍

大跨度斜拉桥的减隔震装置通常采用黏滞阻尼器。黏滞阻尼器属于速度型阻尼器,其阻尼力与速度相关

F=CVα

(7)

式中:F为阻尼力;C为阻尼系数;α为速度指数;V为阻尼器两端的相对运动速度。由式(7)可知,黏滞阻尼器的减震效果由阻尼系数和速度指数共同确定。

3.2 参数优化方法

3.2.1 优化模型

本文的优化模型以系统易损性(SF)最小为目标函数,设计变量包括黏滞阻尼器速度指数α和阻尼系数C。由于塔墩塑形变形能力弱、可修复能力差,需确保支座、斜拉索等易更换构件先于塔墩破坏,即合理损伤路径应为:支座、斜拉索、桥墩、桥塔,模型以该损伤路径为约束条件。本文优化模型如式(8)所示。

3.2.2 基于响应面法的参数优化流程

响应面法是利用试验样本数据拟合结构响应与设计变量之间复杂的隐式函数关系,分析步骤包括试验样本设计、样本试验和响应面拟合[17]。本文采用响应面法建立设计变量(速度指数α、阻尼系数C)与系统易损性(SF)的响应面函数,试验样本设计采用正交设计,样本试验包括非线性时程分析和易损性分析,具体优化流程如图7所示。

图7 基于响应面的参数优化流程

min SF(α,C)

s.t.Pfbear>Pfcable>Pfpier>Pftower

α1≤α≤αn

C1≤C≤Cm

(8)

3.3 响应面函数的建立

3.3.1 样本设计

在工程应用中,大跨度斜拉桥的黏滞阻尼器通常取α=0.2～0.5,C=1 000～8 000[18]。本文分析所用速度指数为0.2、0.3、0.4、0.5,阻尼系数为1 000 kN·(m/s-1)、2 000 kN·(m/s-1)、3 000 kN·(m/s-1)、4 000 kN·(m/s-1)、5 000 kN·(m/s-1)、6 000 kN·(m/s-1)、7 000 kN·(m/s-1)、8 000 kN·(m/s)-α,根据正交设计法选取32个参数样本。

3.3.2 响应面函数拟合

在采用黏滞阻尼器的减震结构中,轻微损伤状态下桥塔损伤概率已降至30%。为方便衡量黏滞阻尼器参数对结构抗震性能的影响,本文选择轻微损伤状态下Pf=20%对应的地震动峰值位移作为响应面函数的因变量,记为PGDsl,0.2,该值越大表明结构发生相同失效概率的地震动强度水平越高。基于易损性分析结果进行响应面拟合,所得斜拉桥系统及构件的响应面如图8所示。

(a) 斜拉桥系统

由图8可知:斜拉桥系统和桥塔的PGDsl,0.2呈先增后减的趋势,存在最优参数使得系统和桥塔抗震性能最优。辅助墩和过渡墩的PGDsl,0.2呈单调递减,但两者的最大变化仅有3%、4%,因此可认为黏滞阻尼器基本不影响过渡墩和辅助墩的抗震性能。各支座的PGDsl,0.2均呈单调递增的趋势,进一步说明斜拉桥各支座的损伤状态具备一定相关性。斜拉索的PGDsl,0.2呈先增后减的趋势,当阻尼力较小时斜拉索的PGDsl,0.2达到峰值。

3.3.3 黏滞阻尼器参数的影响分析

如前所述,黏滞阻尼器参数主要影响斜拉桥系统、桥塔、支座和斜拉索的抗震性能,对过渡墩和辅助墩的抗震性能影响可忽略不计。因此本节主要探讨黏滞阻尼器参数对桥塔、支座、斜拉索和斜拉桥系统抗震性能的影响,以上构件与阻尼器参数的影响规律,如图9所示。

(a) 桥塔

从图9(a)可知,桥塔的PGDsl,0.2存在明显峰值。固定速度指数下,随着阻尼系数的增大,桥塔PGDsl,0.2先增后减。当阻尼系数小于等于3 000 kN·(m/s)-α时,速度指数越大桥塔PGDsl,0.2越大;当阻尼系数大于等于4 000 kN·(m/s)-α时,速度指数越小PGDsl,0.2越小。由图9(b)可知,减隔震体系可显著提升过渡墩支座的PGDsl,0.2,并且阻尼器的速度指数越小、阻尼系数越大,过渡墩支座PGDsl,0.2的提升越明显。由于各支座损伤概率具备相关性,其余支座抗震性能的变化趋势与图9(b)类似。由图9(c)可知,斜拉索PGDsl,0.2存在理论最大值:在同一速度指数下,斜拉索的PGDsl,0.2随阻尼系数的增大先增后减。但在较大阻尼系数下,减震体系斜拉索PGDsl,0.2会低于非减震结构。

比较图9(a)和图9(d)可知,斜拉桥系统和桥塔PGDsl,0.2随阻尼器参数的变化趋势类似,说明斜拉桥整体抗震性能主要受桥塔影响。但相较于桥塔PGDsl,0.2的变化趋势,由于支座PGDsl,0.2的不断增大,斜拉桥系统在不同速度指数下的最优阻尼系数更大,下降段也更平缓。

为分析黏滞阻尼器影响斜拉桥抗震性能的机理,本节统计了32组参数样本下的结构阻尼耗能与最大阻尼力,如图10所示。由图10(a)可知,在固定速度指数下,结构阻尼耗能先减后增;当阻尼系数偏小时,较大速度指数的结构阻尼耗能更大,而当阻尼系数偏大时,较小速度指数的结构阻尼耗能更大。由图10(a)和图9(a)可知,当结构阻尼耗能越大,结构损伤越严重,说明斜拉桥桥塔抗震性能主要受阻尼器耗能效率的影响。而图9(b)中过渡墩支座抗震性能的变化与图10(b)最大阻尼力呈一定相关性,而不受结构阻尼耗能影响,说明支座的抗震性能主要取决于主梁承担的纵向水平力,当纵向水平力越大,主梁纵向变形越小,支座损伤程度越低。

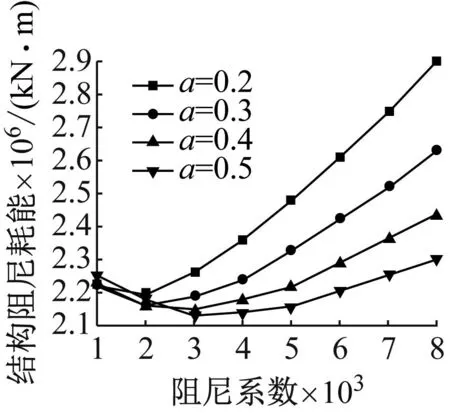
(a) 结构阻尼耗能

3.4 黏滞阻尼器最优参数的确定

根据上述分析可知,固定速度指数下,随着阻尼系数的增大,各支座的抗震性能表现越好,桥塔、斜拉索的抗震性能呈先增后减的趋势,而辅助墩和过渡墩的抗震性能则基本不变。由于斜拉桥的系统损伤概率由各构件的损伤概率共同确定,因此理论上存在一个平衡支座、桥塔和斜拉索损伤概率的最优参数,使得系统损伤概率最低。根据本文的优化模型,合理构件损伤路径为:支座、斜拉索、桥墩、桥塔。由于过渡墩和辅助墩的抗震性能基本不受黏滞阻尼器参数的影响,无法通过参数选择优化其抗震性能,因此本文优化模型的约束条件实际只考虑:支座先于斜拉索破坏、斜拉索先于桥塔破坏。采用遗传算法求解满足该损伤路径的最优参数,最终优化结果为(α=0.5,C=3 828)。最优参数的响应面预测值和有限元分析结果,如表5所示,预测值和有限元分析结果的最大误差仅有2.9%,说明响应面拟合精度较好。

表5 响应面预测和有限元分析结果比较

不同优化结果的比较,优化损伤路径的参数为α=0.5,C=3 828,未优化损伤路径的参数为α=0.5,C=5 783,如图11所示。由图11可知,相较于非减震结构,两种优化结果的桥塔和支座的抗震性能均有明显提升,而辅助墩和过渡墩的抗震性能基本不变。因此黏滞阻尼器主要通过提升桥塔和支座的抗震性能以改善系统抗震性能,系统抗震性能的最优结果是桥塔和支座抗震性能的综合最优结果。在本算例中,斜拉桥系统的最优PGDsl,0.2受限于过渡墩,可通过加强过渡墩的抗震能力进一步提升斜拉桥系统的抗震性能。

图11 不同优化结果的比较

在图11中,仅考虑系统易损性最优、未优化损伤路径时,斜拉桥系统PGDsl,0.2为19.74 cm;优化损伤路径后,斜拉桥系统PGDsl,0.2为19.52 cm。虽然未优化损伤路径的系统抗震性能更优,但斜拉索会先于支座破坏,损伤路径并不合理。因此仅考虑系统易损性最优的结果会高估斜拉桥系统的实际抗震性能。