基于索面布置的扇形索面斜拉桥桥塔稳定性分析

申文杰

（山西省交通规划勘察设计院，山西 太原 030012）

0 引言

自1956年瑞典建成第一座现代斜拉桥——斯特伦松德桥至今，斜拉桥走过了将近半个世纪的历程，关于它的研究、设计和建造工艺有了突飞猛进的发展。斜拉桥作为一种拉索体系，其拉索对斜拉桥的受力有着十分重要的影响。随着斜拉桥跨径的越来越大，其桥塔的高度也变得越来越高，由此而带来的桥塔稳定性问题，也变得十分突出。国内外学者在对斜拉桥稳定方面的研究主要集中于以下几个方面：斜拉桥主梁稳定性研究[1]、斜拉桥施工过程中的稳定性研究[2-3]、斜拉桥桥塔稳定性研究[4-5]、斜拉桥空气静风稳定性研究[6]和斜拉桥空气动力稳定研究。在斜拉桥桥塔本身稳定性的研究方面，国内外学者主要在桥塔稳定性的计算方法、“非保向力”效应以及对索、塔和梁耦合作用的稳定性问题进行了研究，其中苗家武、肖汝诚等利用有限元分析理论研究了不同桥塔刚度、塔跨比及塔上索距对苏通大桥整体稳定性的影响，得出了结构稳定性和动力问题是斜拉桥跨度增大后决定其安全问题的主要影响因素[7]；李国豪教授曾经利用能量法验算了三峡工程中一座斜拉桥的侧向稳定性[8]；斜拉桥设计时基于美观要求，会采用各种各样的索面形式，而当索面形式确定后，桥塔上拉索锚固点位置的不同对桥塔稳定性产生的影响是不同的，而国内外学者在这方面的研究较少，沈志林教授曾经在对独塔单索面斜拉桥稳定性分析时，提出了基于平面分析理论的简化计算方法——古典法和弹性支承法[9]。

扇形索面斜拉桥作为其重要的一支，以其优美的外形成为设计师们钟情的一种斜拉桥桥型，被越来越多的设计建造。因此本文首先依据能量原理导出计入刚性拉杆抗扭刚度的桥塔弹性稳定系数计算公式，然后以某刚性拉杆扇形索面斜拉桥为例，通过桥塔上拉杆锚固点位置的变化来分析索面布置对桥塔稳定性的影响。

1 桥塔侧向稳定性计算

1.1 理论假设

利用能量原理对扇形索面斜拉桥桥塔进行稳定性分析时，选择的假设条件为：

a）主梁的计算采用小变形理论，即认为在桥塔失稳时，忽略主梁的变形。

b）桥塔失稳前后，忽略拉杆的长度变化和拉杆轴线与主梁轴线夹角的变化。

c）桥塔失稳前后，忽略塔梁固结处的位移。

1.2 计算力学模型的简化分析

将桥塔失稳前，桥塔、主梁和斜拉杆处于同一平面内（如图1所示）。通过斜拉杆的联系，将主梁与桥塔联系成一个整体，桥塔侧向失稳时，桥塔将鼓出塔梁杆平面，此时拉杆传递荷载的方向是在不断改变中的，根据假设条件可知，斜拉杆拉力方向始终是指向桥面纵轴线的（如图2所示），这样拉杆拉力会对桥塔侧向稳定性产生影响；同时当桥塔发生失稳时，桥塔上拉杆锚固点会发生位移，使得下拉杆发生扭转，这时拉杆的抗扭刚度也同样会对桥塔侧向失稳产生影响，这两个由于斜拉杆产生的影响对于桥塔来说相当于在其塔身拉杆锚固点处都增加了一个横向弹性支撑（如图3所示）。刚性拉杆扇形索面斜拉桥桥塔失稳时，根据能量法原理，具有的能量有，桥塔弯曲时的弯曲势能，拉杆对桥塔横向弹性支撑的应变能（即拉杆对桥塔失稳的“非保向力”效应），桥塔在自重作用下的外力功，以及桥塔失稳时桥塔拉杆锚固点变位使其在拉杆拉力下做功。

图1 桥塔纵桥向示意图

图2 桥塔侧向失稳示意图

图3 弹性支撑示意图

1.3 桥塔横向弹性稳定系数计算公式推导

根据计算模型简化分析，可知作用于桥塔的外力有桥塔的自重q和斜拉杆拉力Ti（i=1,2,3,4…n），各斜拉杆与主梁水平夹角为αi。

当桥塔失稳时，设桥塔的挠曲线方程为

由于桥塔变形造成的刚性拉杆扭转角度方程为

上述两条曲线方程在边界上必须满足位移边界条件，斜拉杆坐标示意图见图4所示。

根据假设条件，可以在桥塔和斜拉杆平面内将作用于桥塔上的斜拉杆拉力分解成平行于桥塔的竖向力Vi和垂直桥塔的水平力Hi（如图2所示），其中：

图4 拉杆坐标示意图

因此，根据对计算模型分析的结果可知，利用能量法对桥塔稳定性进行计算，需要对桥塔失稳时的桥塔应变能UE、横向弹性支撑应变能UK、桥塔自重的外力势能Vg和斜拉杆分量的外力势能VVi进行计算分析。

通过对桥塔应变能、自重势能、横向弹性支撑应变能以及斜拉杆分量的外力势能的计算分析并整理推导公式得出：

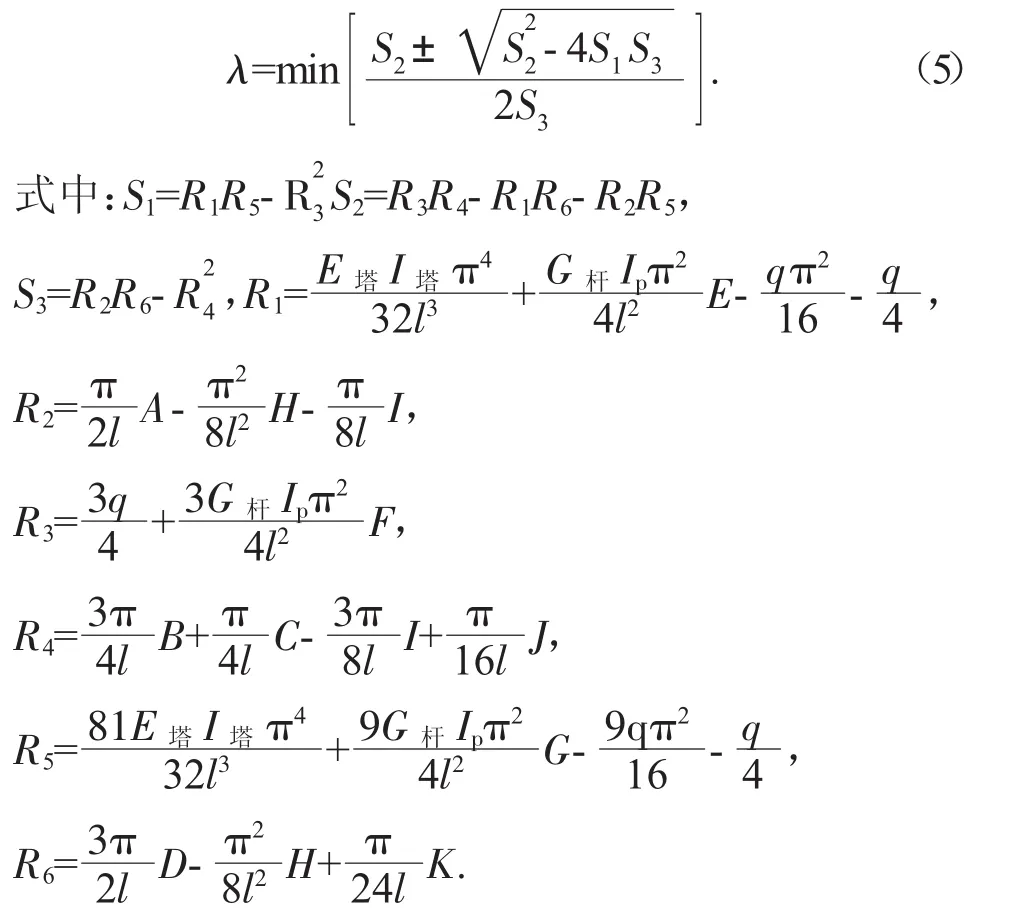
2 算例分析

某斜拉桥采用刚性拉杆扇形索面斜拉桥，该桥为预应力混凝土独塔两跨斜拉桥（如图5所示）。主跨布置为72+72 m，桥梁全长为144 m，采用单塔双索面预应力斜拉索结构，桥塔高47.3 m，桥塔截面尺寸为1.5 m×3 m，桥塔两侧各设8根斜拉杆，拉杆成扇形布置，斜拉杆为预应力混凝土制成的刚性拉杆，该桥具体的尺寸参数见表1～表3。

图5 斜拉桥示意图

表1 桥塔参数表

表2 斜拉杆材料参数表

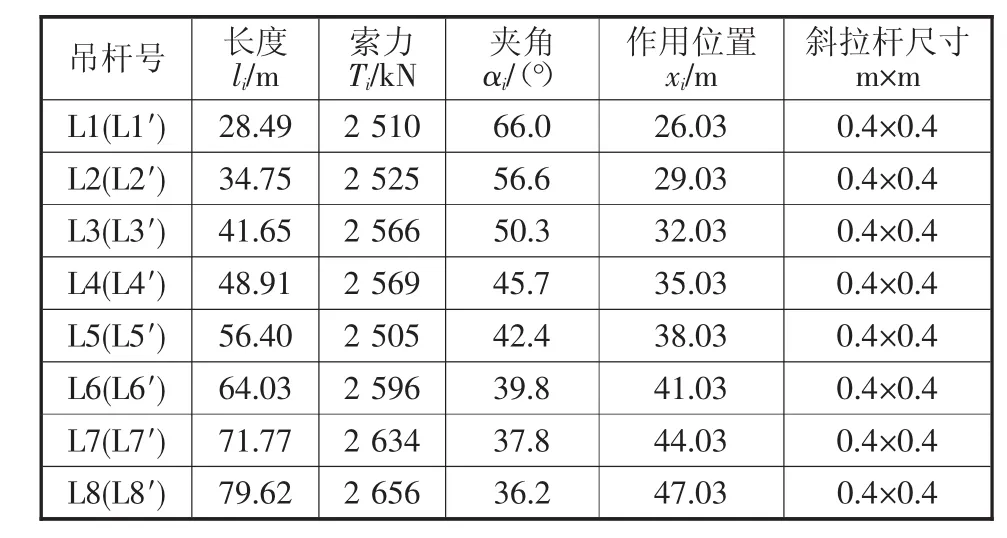
表3 斜拉杆数值表

根据上述推导出的桥塔稳定性系数计算公式对该桥进行理论分析，可知该桥塔的侧向弹性稳定系数 λ1为 λ1=20.42。

若近考虑拉杆的“非保向力”效应，不考虑刚性斜拉杆的抗扭刚度时，该桥塔的侧向弹性稳定系数λ2为 λ2=20.33。

若不考虑拉杆的各种效应，该桥塔的侧向弹性稳定系数λ3为λ3=4.50。

对比上述3个桥塔面外稳定系数可得稳定系数比值ni为：

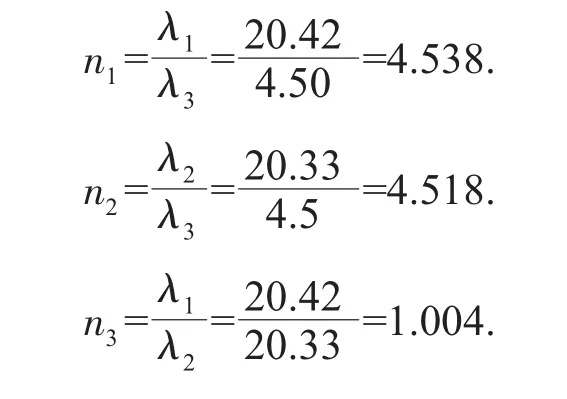
3 影响扇形索面斜拉桥桥塔侧向稳定系数的参数分析

通过刚性拉杆扇形索面斜拉桥桥塔的侧向弹性稳定系数公式的推导，可以看出桥塔上斜拉杆锚固点间距对弹性稳定系数有影响，因此以上述算例中斜拉桥的尺寸为基本参数，对桥塔拉杆锚固点以等差间距布置的扇形索面斜拉桥讨论拉杆锚固点间距对桥塔侧向弹性稳定性的影响。

在对等差间距布置的扇形索面斜拉桥桥塔侧向弹性稳定性进行讨论时，取d1为桥塔上拉杆L8与拉杆L7之间的间距，d为桥塔拉杆锚固点间距的等差值，λ1、λ2、λ3、n1、n2和 n3的定义同 2 中算例。通过已推导出的桥塔侧向弹性稳定性理论公式分析d1和d对桥塔稳定系数λ1、λ2和λ3及桥塔稳定系数比值n1、n2和n3的影响来探讨扇形索面拉杆间距对桥塔稳定性影响。

通过对计算结果进行分析可知：

a）当 0.5 m≤d1≤1.4 m时，各 λ1-d曲线（即桥塔稳定系数λ1与桥塔锚固点间距方差d曲线）变化趋势一致，随着等差值d的增加，λ1-d曲线呈“S”型变化。

当1.4 m＜d1≤3.8 m时，各λ1-d曲线（即桥塔稳定系数与桥塔锚固点间距方差曲线）变化趋势一致，随着等差值d的增加，λ1-d曲线呈“U”型变化。当3.8 m＜d1≤6.0 m时，各λ1-d曲线（即桥塔稳定系数与桥塔锚固点间距方差曲线）变化趋势一致。

b）对比计算结果可知，λ1-d曲线与 λ2-d曲线变化趋势一致，且当 d 和 d1相同时，λ1＞λ2。

c）λ3-d曲线随d的增加而增加，并且d1愈大增长趋势愈大。

d）当 0.5 m≤d1≤1.0 m时，各 n1-d曲线（即桥塔稳定系数比值n1与桥塔锚固点间距方差d曲线）变化趋势一致，随着等差值d的增加，λ1-d曲线呈“S”型变化；当1.0 m＜d1≤4.4 m时，各n1-d曲线（即桥塔稳定系数比值n1与桥塔锚固点间距方差d曲线）变化趋势一致，随着等差值d的增加，n1-d曲线呈“U”型变化；当 4.4 m＜d1≤6.0 m时，各 n1-d曲线（即桥塔稳定系数比值n1与桥塔锚固点间距方差d曲线）变化趋势一致。

e）n1-d曲线与n2-d曲线变化趋势一致，且当d和 d1相同时 n1＞n2。

f）当 0.5 m≤d1≤2.6 m时，各 n3-d曲线（即桥塔稳定系数比值n3与桥塔锚固点间距方差d曲线）变化趋势一致，随着等差值d的增加，n1-d曲线呈“凸”型曲线变化。当2.6 m＜d1≤6.0 m时，各n3-d曲线变化趋势一致。

4 结论

本文通过刚性拉杆扇形索面斜拉桥桥塔稳定性系数计算公式的推导，及分析斜拉桥拉索位置参数对桥塔稳定性影响，得到以下结论：

a）根据能量法原理，刚性拉杆扇形索面斜拉桥桥塔失稳时具有的能量有：弯曲势能、应变能、外力功等，其中应变能即拉杆对桥塔失稳的“非保向力”效应。对于刚性拉杆扇形索面斜拉桥，拉杆的抗扭刚度会提高桥塔稳定性。考虑拉索“非保向力”效应计算出来的桥塔稳定性系数比未考虑桥塔稳定性系数增加2.8～9.5倍。考虑拉索“非保向力”效应的桥塔稳定性系数时，计入拉杆抗扭刚度桥塔稳定性系数比未计入的要提高大概0.5‰～4.3‰。

b）对于刚性拉杆扇形索面斜拉桥，桥塔上拉索锚固点位置对桥塔稳定性有影响，并且与桥塔稳定性系数呈非线性关系。

c）通过刚性拉杆扇形索面斜拉桥桥塔的侧向弹性稳定系数公式的推导，以及对计算结果的分析建议在扇形索面斜拉桥拉索锚固点采用等差数列布置时，桥塔拉杆锚固点间距等差d的选取范围为[0 m，0.4 m]，锚固点间距的基数（即顶端第一根拉杆与第二个拉杆的间距）d1的选取范围为[0.5 m，1.1 m]。当斜拉桥拉杆在建议范围内布置时，计入拉杆“非保向力”作用的桥塔稳定性系数较大，能够充分发挥拉杆的扭转和拉杆拉力的虚拟弹簧效应，并且在该范围内，桥塔拉杆锚固点间距的变化对桥塔侧向弹性稳定系数影响较小。拉杆“非保向力”效应在扇形索面斜拉桥拉索位置设计时，应当予以考虑。

d）对大跨度桥梁结构稳定性研究时还需考虑非线性和局部稳定性，对于大跨度斜拉桥桥塔稳定性的计算分析还有待进一步研究。