盐水液滴蒸发析晶实验研究及其反应工程法的单液滴模型

张斌, 郭朋华, 牛衍赓, 邹瀚森

(西安交通大学能源与动力工程学院, 710049, 西安)

喷雾蒸发现象广泛存在于能源、动力、化工、食品及医疗等领域,建立单液滴蒸发模型是对喷雾蒸发过程进行数值模拟研究的基础。现阶段,盐溶液喷雾蒸发过程的数值研究多应用于含盐废水处理[1-3]和海水淡化[4-5]等方面,但因其多局限于蒸发浓缩阶段,不涉及复杂的晶体析出过程,所以通常采用纯水液滴蒸发运动模型或只考虑浓缩而忽略结晶[6]来代替。实际上,盐水液滴蒸发过程中液滴密度会逐渐变化,同时由于结晶析出的复杂性[7],使得液滴蒸发运动特性与纯水液滴有着较大区别,因此,使用纯水液滴蒸发模型对盐水喷雾蒸发过程进行数值模拟会产生较大偏差。

单液滴蒸发实验是建立盐水液滴蒸发模型的有效手段,目前常用的液滴蒸发实验方法包括自由落体法[8]、薄层干燥法[9]、声悬浮法[10-11]、固着表面法[12-13]、悬挂法[14-15]等,前4种方法均能从不同程度上揭示液滴蒸发运动的内、外部规律,然而却都无法得到蒸发过程中液滴质量、温度和粒径等全参数的变化。悬挂法将液滴悬挂于可变挠度的悬丝端部,根据悬丝的挠度变化测量液滴的质量变化,特别适用于变密度液滴蒸发过程中质量的测量。

针对含析出性溶质液滴的蒸发过程,常见的计算模型有特征干燥曲线模型(CDC)[16-18]、反应工程法模型(REA)[19-20]、阶段理论计算模型[21-22]和分子动力学模型[23-24]等。CDC和REA模型[25]均基于集总参数思想,忽略了蒸发过程中液滴内部的传热传质,大大简化了计算过程。然而,针对不同的蒸发工况,CDC模型需要分别建模且临界含湿量常常难以确定,模型普适性差。另外,复杂的三阶段模型[22]、四阶段模型[21]和分子动力学模型更适合于描述单个液滴的蒸发过程,但因其计算量巨大,不便应用于工业级大规模喷雾蒸发的数值计算。REA模型为半经验模型,由实验测量获得液滴蒸发过程的质量、温度和直径等参数的变化规律,据此可计算得到液滴表面活化能和直径随液滴干基含水率的函数关系,进而预测液滴蒸发结晶过程。Chen等[26]和Patel等[20]均指出,相同初始干基含水率的同种溶液液滴,可适用于同样的相对活化能分布规律,而不受蒸发工况及初始粒径的影响,这使得REA模型具有更高的普适性,尤其适于盐水溶液喷雾蒸发的数值计算。对单液滴蒸发过程中液滴质量、粒径、温度的变化进行精确测量,是准确建立REA模型的前提和基础,但目前文献中尚缺乏可用于建立盐水溶液REA模型的实验数据。

因此,本文基于悬挂法搭建了可实现质量、粒径、温度同时测量的单液滴蒸发实验平台,分析了液滴悬挂装置振动的频谱特性及其对液滴质量测量的影响规律,并采用滤波的方法消除了振动信号对质量测量的影响,获得了初始质量分数为10%的NaCl溶液液滴蒸发的质量、温度、粒径和形貌等热动力学参数,并根据实验数据建立和验证了对应的REA模型。

1 REA原理概述

图1给出了单液滴蒸发过程的示意图。在蒸发过程中,水分子克服表面束缚形成水蒸气,带走热量并降低液滴温度的同时,在液滴表面形成低温区和高浓度区,继而在对流和扩散的作用下完成液滴与周围环境的热质交换。

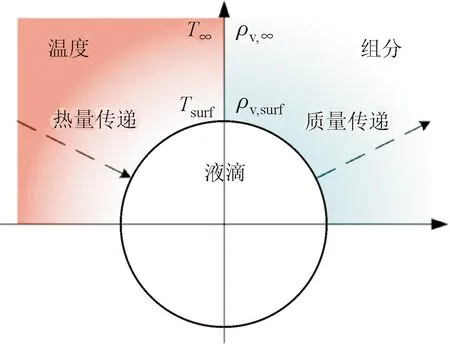
图1 液滴蒸发过程热质传递示意图

REA模型的关键思想是将水分子所克服的表面束缚量化为活化能ΔE,而液滴表面的相对湿度φsurf可写成表面温度Tsurf和活化能ΔE的函数,即

(1)

式中:φ为相对湿度;ΔE为活化能;T为温度;R=8.314 J/(mol·K)为气体常数;下标surf表示液滴表面。

根据对应温度下的饱和蒸汽浓度ρv,sat(Tsurf),可求得液滴表面蒸汽浓度ρv,surf,表示为

ρv,surf=φsurfρv,sat(Tsurf)

(2)

根据对流传热传质方程,液滴表面与周围环境间的热质传递可描述如下

(3)

(4)

式中:m为液滴质量;cp为液滴比热容;h和hm分别为对流传热系数和对流传质系数;Sp为液滴表面积;Lv为水蒸气的汽化潜热;下标p表示液滴集总参数,sat表示饱和,v表示水蒸汽参数,∞表示环境参数。

在上述过程中,相对活化能ΔE是预测液滴表面蒸汽浓度的关键。计算对流传热系数h和对流传质系数hm需要用到雷诺数Re,而计算雷诺数要求在蒸发过程中液滴直径D为已知量。因此,通过实验测量建立REA模型的思路是上述过程的逆过程。由式(1)、(2)、(4),可得到由实验数据计算的液滴表面活化能公式,写为

(5)

从式(5)可以看出,质量蒸发率、液滴表面积以及表面温度是建立模型的核心参数,可根据实验获得的质量、温度、粒径等参数计算得到。

为处理不同蒸发环境下、不同初始体积的液滴,采用归一化方法引入相对活化能(ΔE/ΔEe)和无量纲粒径(D/D0),其中,D0为液滴的初始直径,ΔEe为蒸发结束时液滴与环境平衡状态下的活化能,可由式(1)推导得到,表示如下

ΔEe=-RT∞lnφ∞

(6)

液滴的蒸发进程采用干基含水率X表示,即液滴中水的质量mw与干盐质量ms的比值。根据液滴质量数据,得到不同时刻液滴干基含水率的表达式为

(7)

平衡状态下的干基含水率Xe约为0.3,在建立模型时,采用干基含水率与平衡干基含水率之差,即干基自由水含水率(X-Xe)来模拟蒸发过程。

综上所述,根据不同时刻的液滴表面活化能、直径和干基含水率数据,就能建立REA模型,即相对活化能和无量纲粒径随液滴干基自由水含水率的变化关系。

2 实验装置及方法

本文搭建了如下所述的单液滴蒸发实验装置,以记录液滴蒸发过程的热动力学参数,并据此建立了NaCl溶液液滴蒸发模型。

2.1 实验装置概述

如图2和图3所示,实验系统包含气路系统、温度采集系统、图像采集系统和液滴悬挂装置。实验中,气流由空气发生器产生,并由内置的湿度控制装置调控,经转子流量计和空气加热器,以稳定的流速和温湿度流经实验段;液滴温度和环境温度由热电偶测量,经温度变送器和采集卡传输到计算机;液滴质量和直径由正位摄像机拍摄得到,液滴蒸发过程中尤其是析晶过程的形貌变化则由侧位摄像机记录。

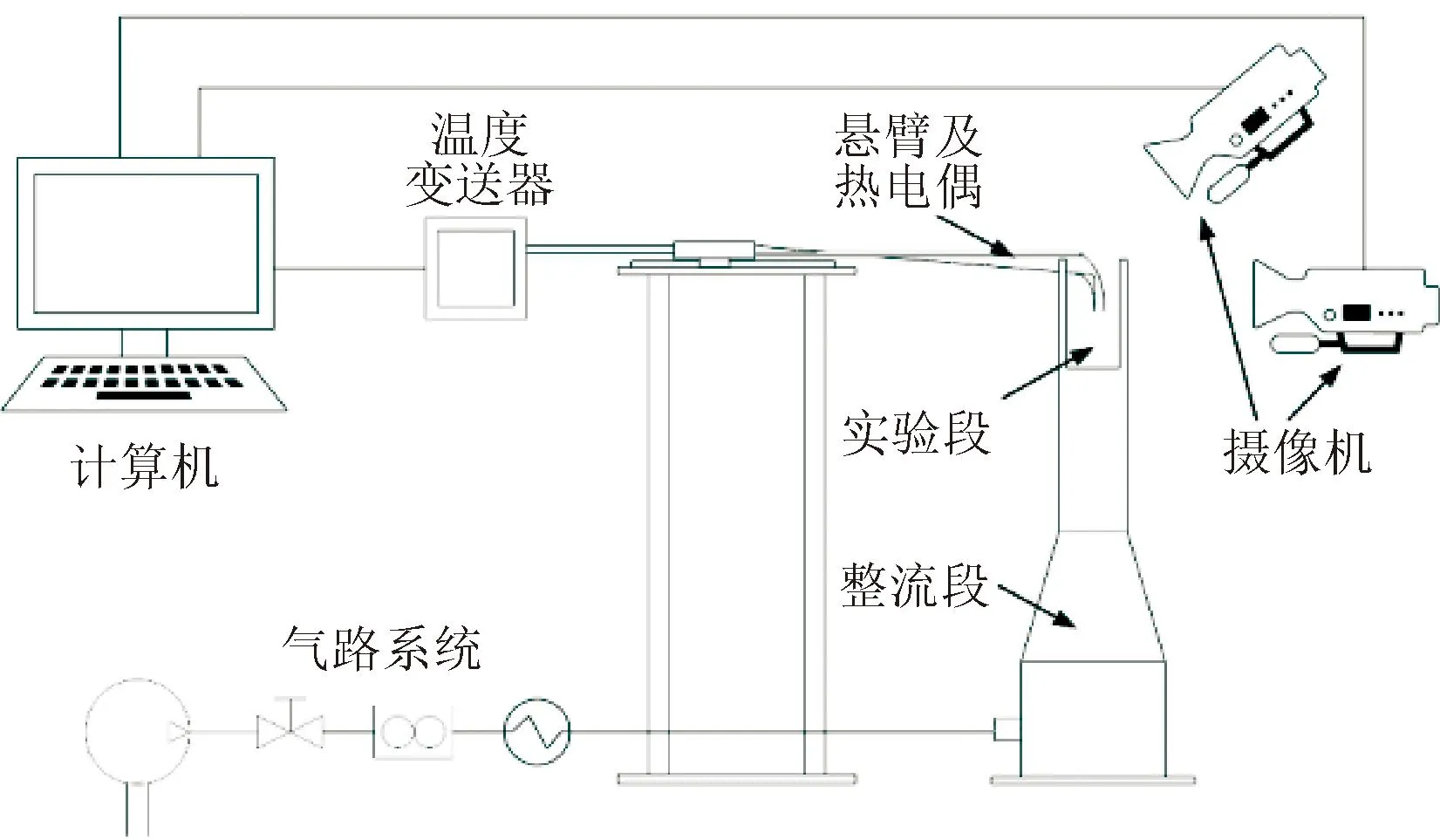
图2 单液滴蒸发实验装置示意图

液滴悬挂装置如图4所示,其基体由导轨滑块装置构成,外附亚克力管、不锈钢丝以及2个热电偶。其中,不锈钢丝呈悬臂状态,以其挠度变化作为液滴质量的测量依据;液滴温度热电偶通过数个节点粘附于不锈钢丝上,随不锈钢丝一起运动,并在测温节点处做适当处理以便悬挂;环境温度热电偶通过亚克力管伸入环境中,并与液滴温度热电偶保持同一高度。

2.2 实验方法

实验中,液滴通过微量进液器生成,然后迅速转移并悬挂在热电偶测温节点处,在恒定的气流条件下完成蒸发结晶过程。正位摄像机在一定的灯光条件下得到悬挂装置标记点以及整个液滴的黑白图像,侧位摄像机记录液滴蒸发过程中的形貌变化和结晶方式。一组典型的液滴照片如图5所示。

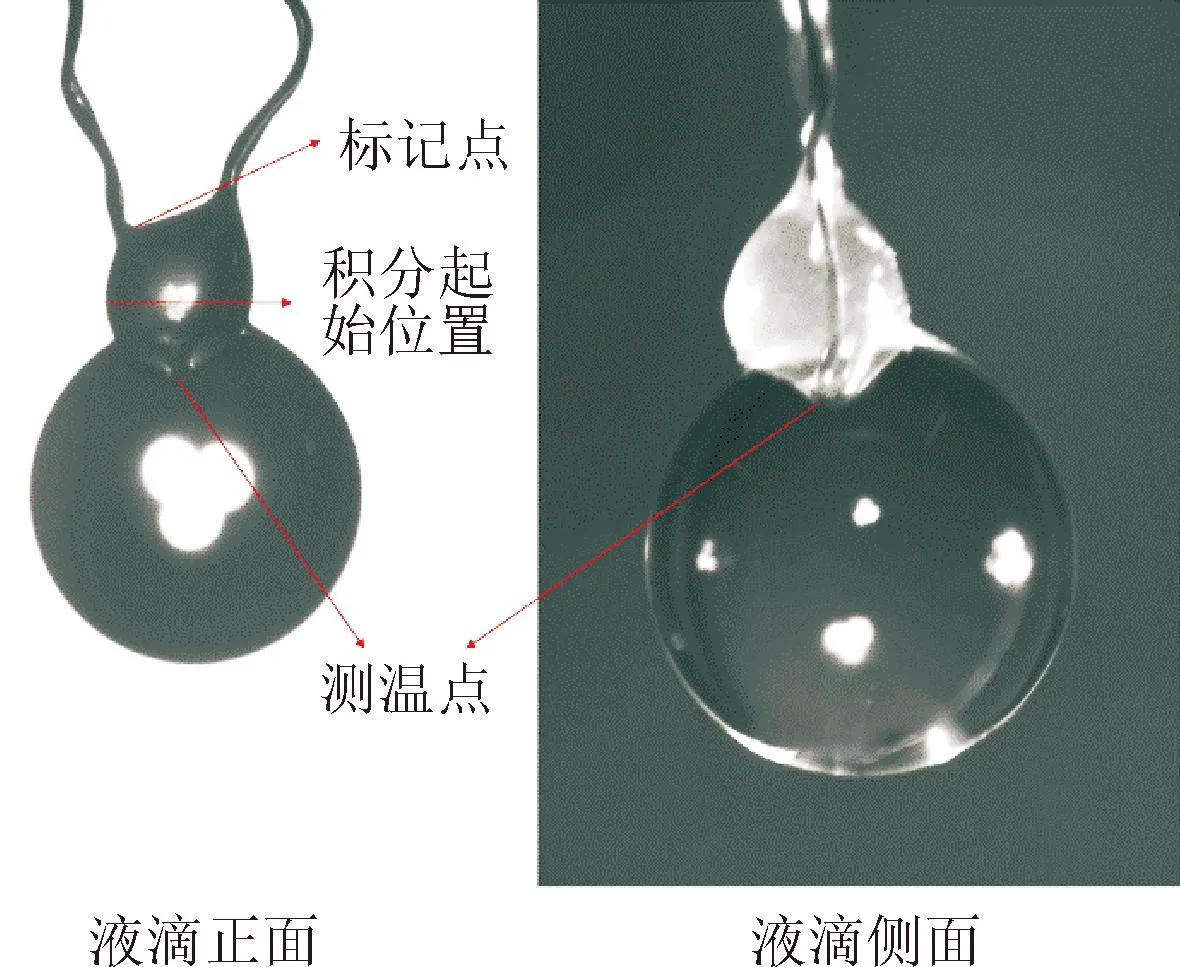
图5 液滴正面和侧面照片

根据不锈钢丝挠度随自由端质量变化的原理测得液滴质量。在实验开始前,需对液滴悬挂装置的位置-质量关系进行标定,液滴质量m随像素ΔP的变化关系使用线性拟合(R2=0.999),表示如下

m=111.59ΔP

(8)

采用积分等效直径方式计算液滴直径,首先拍摄系列标准宽度,然后对二值化并填充过的正面图像从图中起始位置向下进行旋转积分,得到液滴和悬挂头的体积,再用得到的体积减去初始时刻无液滴时积分得到的悬挂头体积,即液滴的实际体积,从而求得液滴直径。

液滴温度和环境温度均采用热电偶(Omega CHAL-002)测量,经温度变送器(Omega DRST-UN)和采集卡(ART USB3103A)传输到电脑端并保存。本文采用集总参数假设,即液滴内部温度分布处处相等,则液滴的毕渥数Bi可写为

(9)

式中:λ为液滴内部的导热系数。

根据式(9),液滴毕渥数为0.09小于0.1,即液滴内部温度分布近似均匀,因此热电偶测温点在液滴内的相对位置对测温结果的影响可以忽略不计。

2.3 实验方案

研究发现,液滴悬挂装置在气流作用下的振动对液滴蒸发过程中的质量测量有显著影响,因此,本文首先对液滴悬挂装置的流致振动特性进行研究,通过离散傅里叶变换的方法,对比分析了有、无液滴悬挂时系统振动的频域特性。随后,对测量得到的质量信号进行低通滤波,对比不同滤波频率下的滤波效果,并选择合适的滤波频率。

在上述分析的基础上,对初始质量分数为10%的NaCl溶液进行单液滴蒸发实验,得到不同初始粒径下液滴蒸发过程中质量、温度和粒径的变化数据,据此建立描述NaCl溶液液滴蒸发过程的REA模型,并观测液滴蒸发过程尤其是结晶过程中液滴的形貌变化。实验工况设置见表1。

表1 单液滴蒸发实验工况设置

2.4 实验误差分析

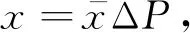
(10)

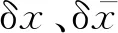
对K型热电偶进行标定后,得到的测温精度为±0.2℃,各参数测量的不确定度如表2所示。

3 实验结果与分析

3.1 悬臂系统振动的频域分析

图6和图7为无液滴悬挂时,实验数据与采用不同截止频率fL低通滤波后计算得到的质量信号和幅频特性曲线对比。由图6可见,由于无液滴悬挂时,悬挂装置自身会在气流的作用下做无规则振动,导致得到的液滴质量有±0.1 mg的误差,液滴蒸发率的计算值存在较大波动。

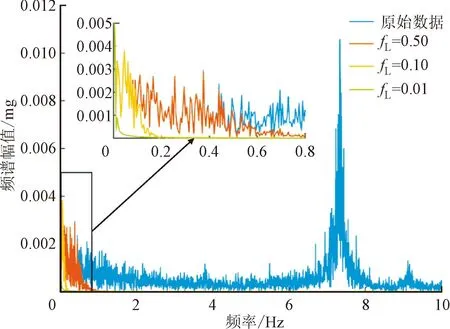
图7 不同截止频率滤波前后幅频特性曲线对比

对质量信号做离散傅里叶变换,得到信号波动的幅频特性曲线,如图7所示。可以看出,信号在频率f=7.34 Hz处存在谐振峰值,即达到液滴悬挂装置的固有频率。此外,信号在f<2 Hz时还存在低频噪声,对质量的测量也存在一定的干扰。

综上,随着截止频率的降低,滤波对低频段噪声的消除效果更好,得到的质量变化曲线更光滑。因此,选取0.01 Hz作为后续对质量数据进行滤波处理的截止频率。

图8和图9为悬挂不同初始质量液滴时,滤波前后的质量信号及幅频特性曲线对比。可见,滤波后的质量变化曲线平滑性更好,且能保留曲线真实的变化趋势。从频域角度分析,悬挂不同质量的液滴会导致装置具有不同的谐振频率,在本实验工况范围内,该频率区间为6.61～7.34 Hz,皆可采用低通滤波消除谐振频率下的振动信号;在低频段,悬挂不同质量液滴时频谱图的区别主要体现在f<0.02 Hz阶段,而该段频谱图在每组数据滤波前后近似重合,说明滤波保留了不同悬挂质量下的主频。

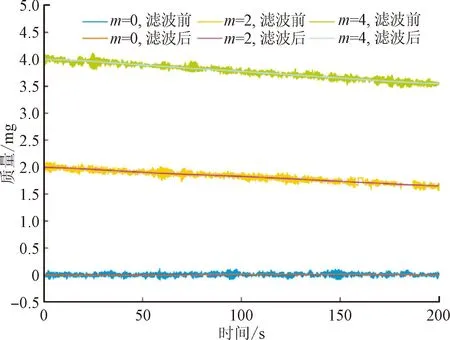
图8 不同初始质量液滴滤波前后质量信号对比

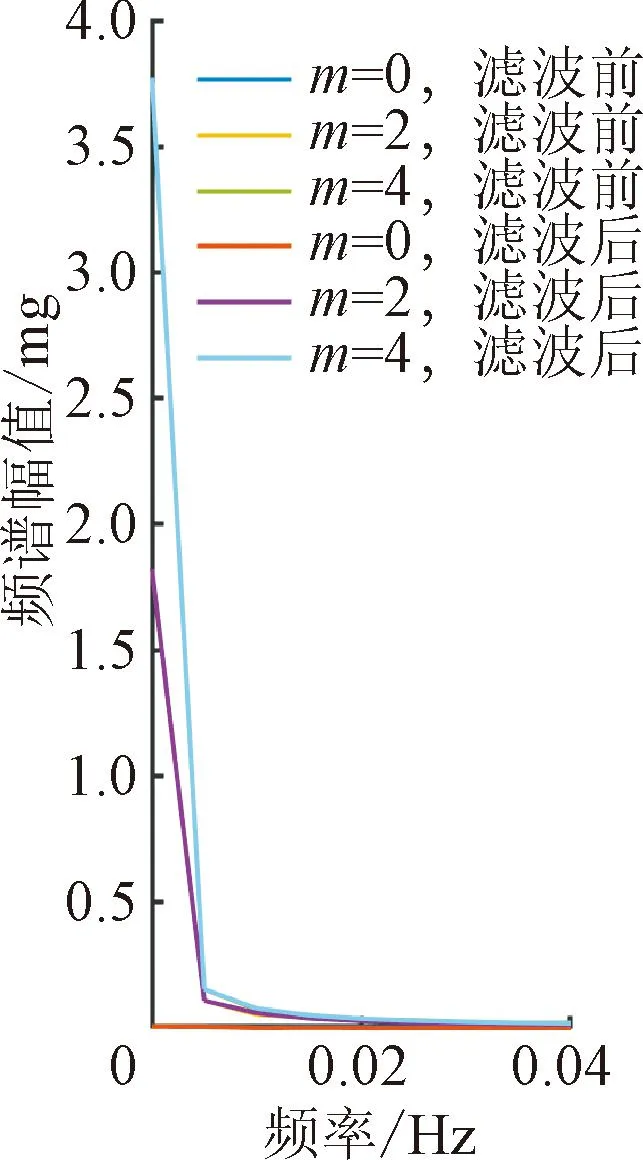
(a)低频高幅值段

图10给出了不同初始质量液滴滤波前后,计算得到的蒸发率对比。由于滤波前的质量数据存在±0.1 mg 的波动,导致计算得到的蒸发率波动较大且存在负值,无法反映真实情况,为后续建模带来困难;而通过低通滤波,蒸发率波动大幅减小,且均收敛到正值。

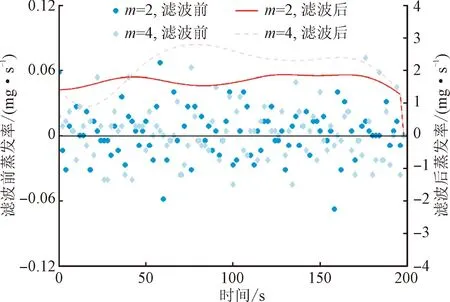
图10 不同初始质量液滴滤波前后蒸发率对比

通过以上对质量信号、振动频率特性以及蒸发率的分析,发现采用低通滤波处理,既能保留质量变化信号的主要特征,又能最大程度地消除干扰信号的影响,为蒸发率的准确计算提供了保障。

3.2 盐水(NaCl溶液)液滴蒸发实验结果分析

3.2.1 液滴蒸发过程质量变化

图11为两种不同初始体积的液滴在蒸发过程中质量和蒸发率随时间的变化曲线。图12为蒸发过程中单位表面积的水分蒸发率变化图。如图所示,随着液滴蒸发过程的进行,液滴的表面积逐渐减小,液滴蒸发率也随之降低,但单位面积的蒸发率有所升高,这是因为液滴直径减小时,对流传质系数有小幅提高。当液滴表面有结晶生成时,液滴内80%的水分已完成蒸发。随着晶体的生长,液滴蒸发的有效面积减小,导致蒸发率下降,直至液滴表面被完全包覆,水分蒸发掉90%。剩余水分通过孔隙结构,渗透至盐壳表面继续蒸发,且蒸发率持续下降,直至与完全包覆前相比约减小一个数量级,此时认为蒸发过程结束。

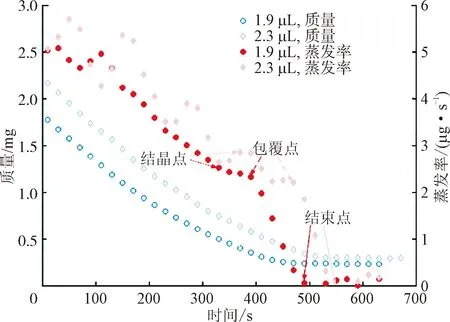
图11 不同初始体积液滴蒸发过程的液滴质量和蒸发率

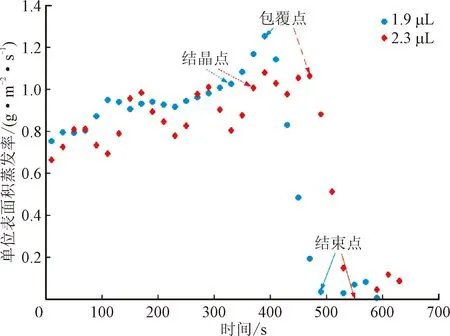
图12 不同初始体积液滴蒸发过程单位表面积的水分蒸发率

3.2.2 液滴蒸发过程温度变化

图13展示了两种不同初始体积液滴蒸发过程的温度变化。由图可见,当液滴进入蒸发环境后,迅速变化至湿球温度;由于水分不断蒸发,NaCl在液滴表面富集,表面盐浓度增大,水分蒸发阻力增大,导致蒸发速率降低[27]。与此同时,液滴的热容降低,液滴温度缓慢升高。在结晶点位置,液滴的平均浓度高于NaCl溶液的饱和浓度,处于过饱和状态,与Gregson等[28]在文献中给出的实验结论相吻合。此时,宏观上可见NaCl晶体出现在液滴表面,在过饱和度的影响下,结晶速率较快,伴随着结晶放热,液滴开始小幅温升。随着过饱和溶液中NaCl结晶的析出,液滴表面的溶液浓度回落,结晶的驱动力减小,结晶放热速率减慢。此外,由于表面浓度下降,蒸发阻力减小,单位表面积的蒸发速率上升,蒸发带走的热量增大,导致液滴温度小幅回落。随着NaCl晶体生长并逐渐覆盖液滴表面,蒸发阻力逐渐增加,液滴温度回升。当液滴表面形成完整盐壳时,液滴内水分需通过孔隙渗透至盐壳表面才能继续蒸发,蒸发阻力急剧增大,液滴温度迅速上升,最终到达环境温度,蒸发过程结束。

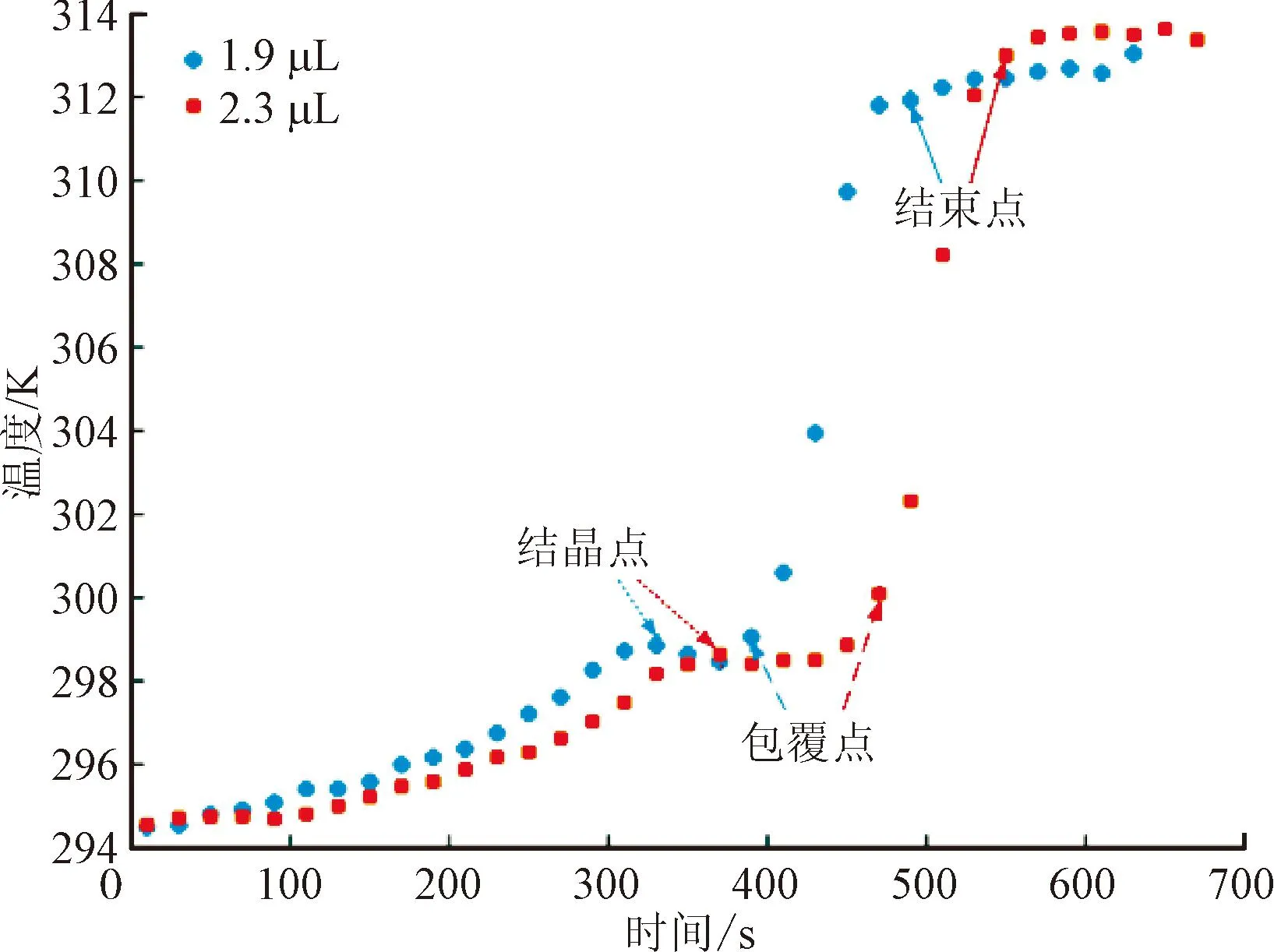
图13 不同初始体积液滴蒸发过程的温度变化

3.2.3 液滴蒸发过程粒径和形貌变化

图14为两种初始体积的液滴在蒸发过程中的粒径变化图。图15为初始体积为2.3 μL时,实验得到的液滴形貌变化图。

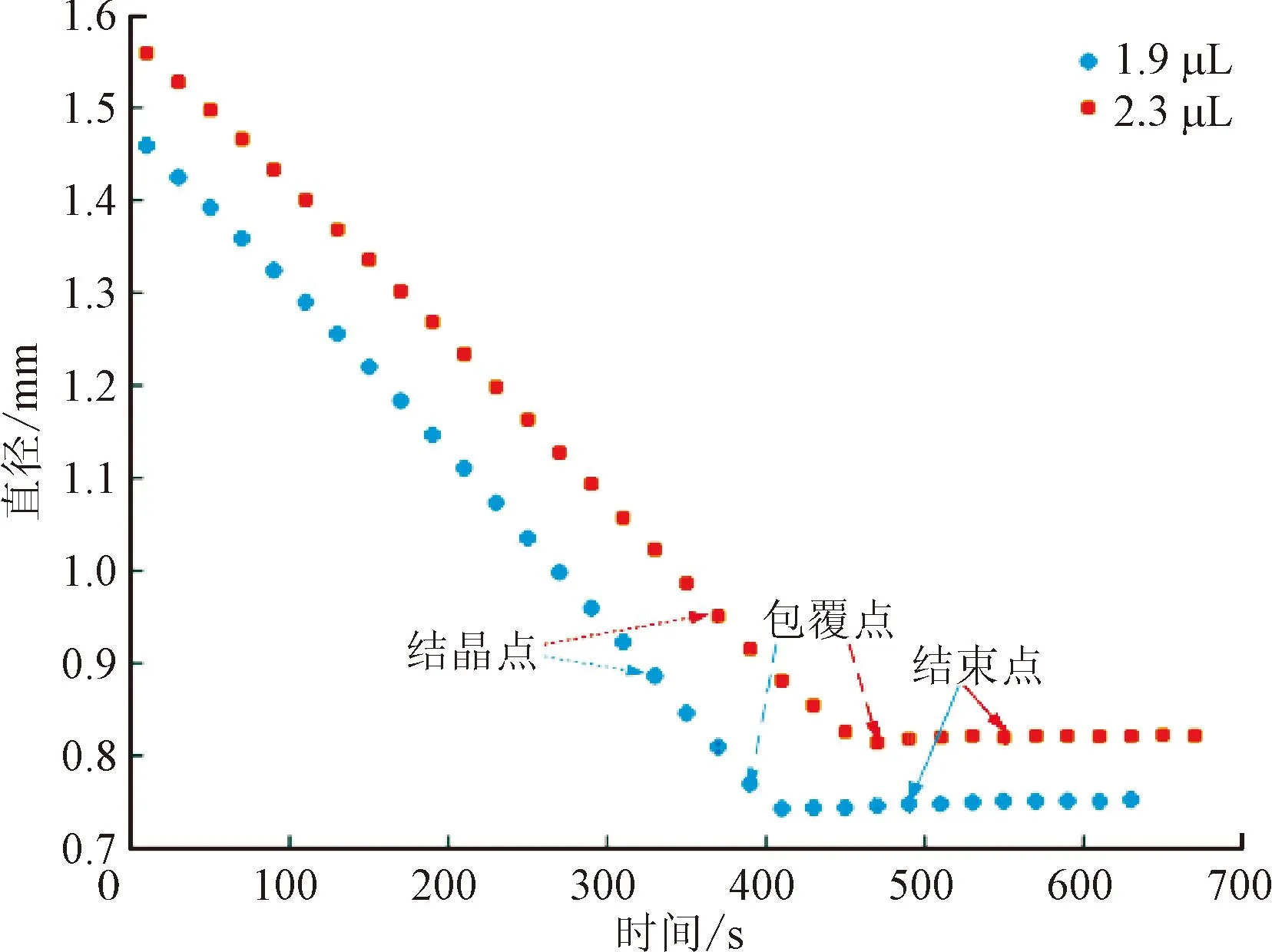
图14 不同初始体积液滴蒸发过程中粒径变化

如图所示,随着蒸发过程的进行,液滴粒径逐渐减小,当浓缩到一定程度时,NaCl晶体首先在液滴底部生成,此时80%占比的液滴直径已完成变化。随后,向上生长并逐渐覆盖液滴的表面。当液滴表面被完全覆盖后,液滴形貌及粒径不再变化,剩余少量水分通过孔隙不断输运到表面,蒸发过程结束。

3.3 REA模型建立

如上所述,建立REA模型的关键,是获得相对活化能和无量纲粒径随蒸发过程液滴干基自由水含水率的函数关系。

图16所示为液滴相对活化能随蒸发过程的变化曲线。由图可见,不同初始体积的溶液液滴具有相同的活化能变化趋势。在液滴蒸发的初始阶段,由于含水率较高,所以相对活化能较低;随着蒸发过程的进行,液滴中的水分不断蒸发,液滴表面的氯离子和钠离子富集,增大了水分子蒸发的阻力,导致相对活化能缓慢增大。随着蒸发继续进行,NaCl晶体开始在液滴表面析出,此时蒸发阻力急剧增大直至蒸发结束。

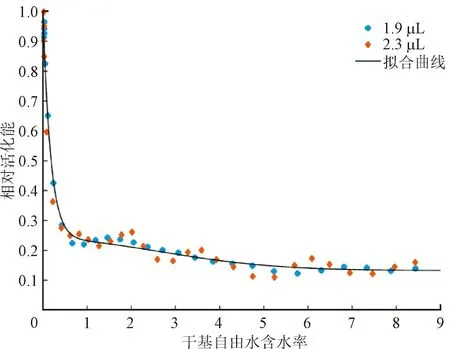
图16 不同初始体积液滴相对活化能变化曲线

图17给出了液滴无量纲直径随蒸发过程的变化曲线。如图所示,两种初始粒径的液滴具有相同的变化规律。随着液滴水分的蒸发,无量纲直径减小,但并非简单的线性规律。当液滴底部出现结晶后,液滴直径继续减小,直至液滴表面被盐壳完全包覆,晶体向内生长,液滴内部的水分通过盐壳孔隙渗透到液滴表面蒸发,继而在液滴表面生成少量结晶,并导致液滴直径略微扩大。

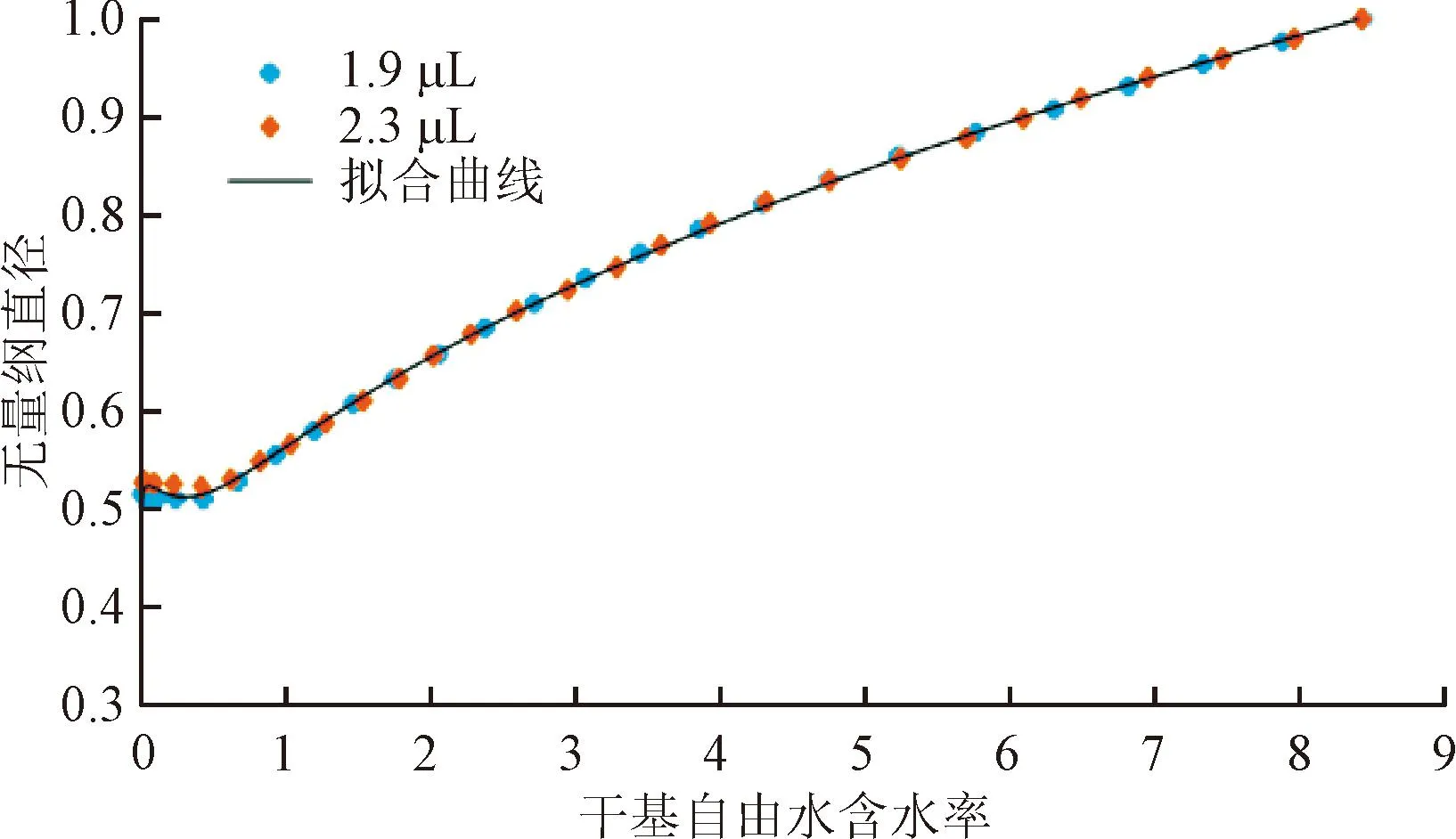
图17 不同初始体积液滴无量纲直径变化曲线

通过函数拟合,得到相对活化能和无量纲粒径随液滴干基自由水含水率的函数关系式,拟合方差分别为0.981和0.999,结果可靠性较高。至此,本文建立了初始质量分数为10%NaCl溶液的REA模型,表述如下

(11)

(12)

3.4 REA模型验证

为验证上文得到的初始质量分数为10%NaCl液滴蒸发REA模型的有效性,本文采用自编程和嵌入Fluent两种方式,对实验工况下液滴蒸发过程中质量的变化进行了计算与验证。

自编程算法采用显式时间推进法,对式(3)和式(4)进行求解,其中液滴表面的物性参数由1/3混合准则[29]计算,得到了液滴蒸发过程中质量和温度等参数的变化规律。

使用Fluent软件对单液滴蒸发进行了非稳态数值模拟,通过使用UDF自定义函数的DEFINE_DPM_VP_EQUILIB宏更改液滴表面水蒸气质量分数的方式,嵌入了盐水液滴蒸发的REA模型。图18对比了不同初始体积的液滴蒸发第200 s时环境空气中水蒸气质量分数分布。由图可见,初始体积越大的液滴,其蒸发的中心水蒸气质量分数更高,尾迹区水蒸气的影响范围更大,表明液滴具有更高的蒸发速率,这与3.2.1小节得到的液滴蒸发率规律相一致。

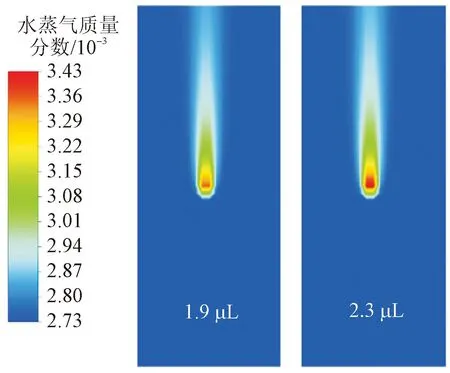
图18 不同初始体积液滴蒸发第200 s时环境空气中水蒸气质量分数对比

图19和图20为不同初始体积液滴质量和温度的计算值与实验值对比。由图可见,数值计算对液滴蒸发过程的质量变化趋势和残余颗粒质量的预测均较为准确,对液滴温度预测的偏差主要发生在结晶阶段,最大相对误差小于8%,这主要是由于数值计算中缺乏准确的变浓度溶液比热容数据,以及未考虑结晶过程中的放热效应。

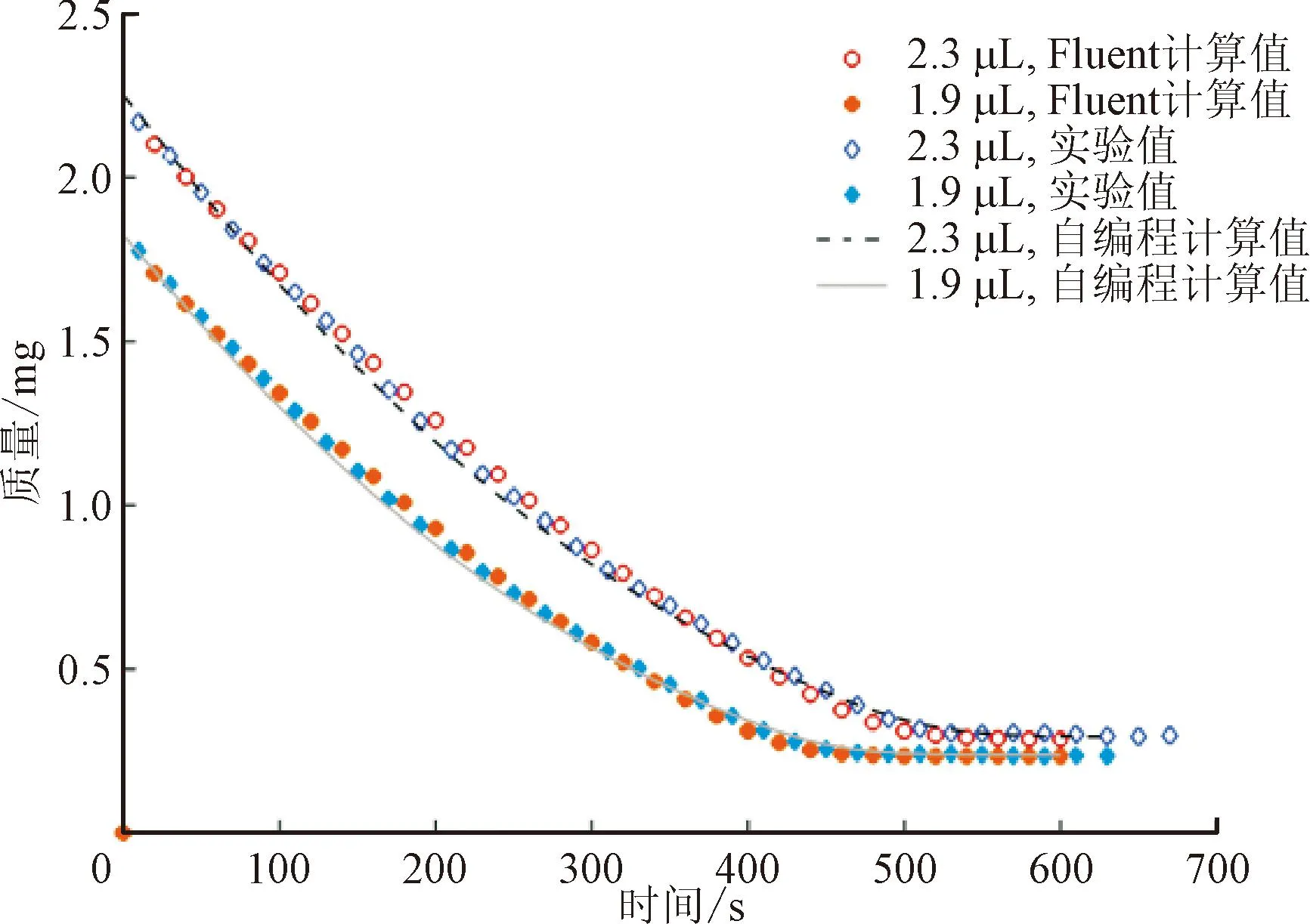
图19 不同初始体积液滴质量计算值与实验值验证

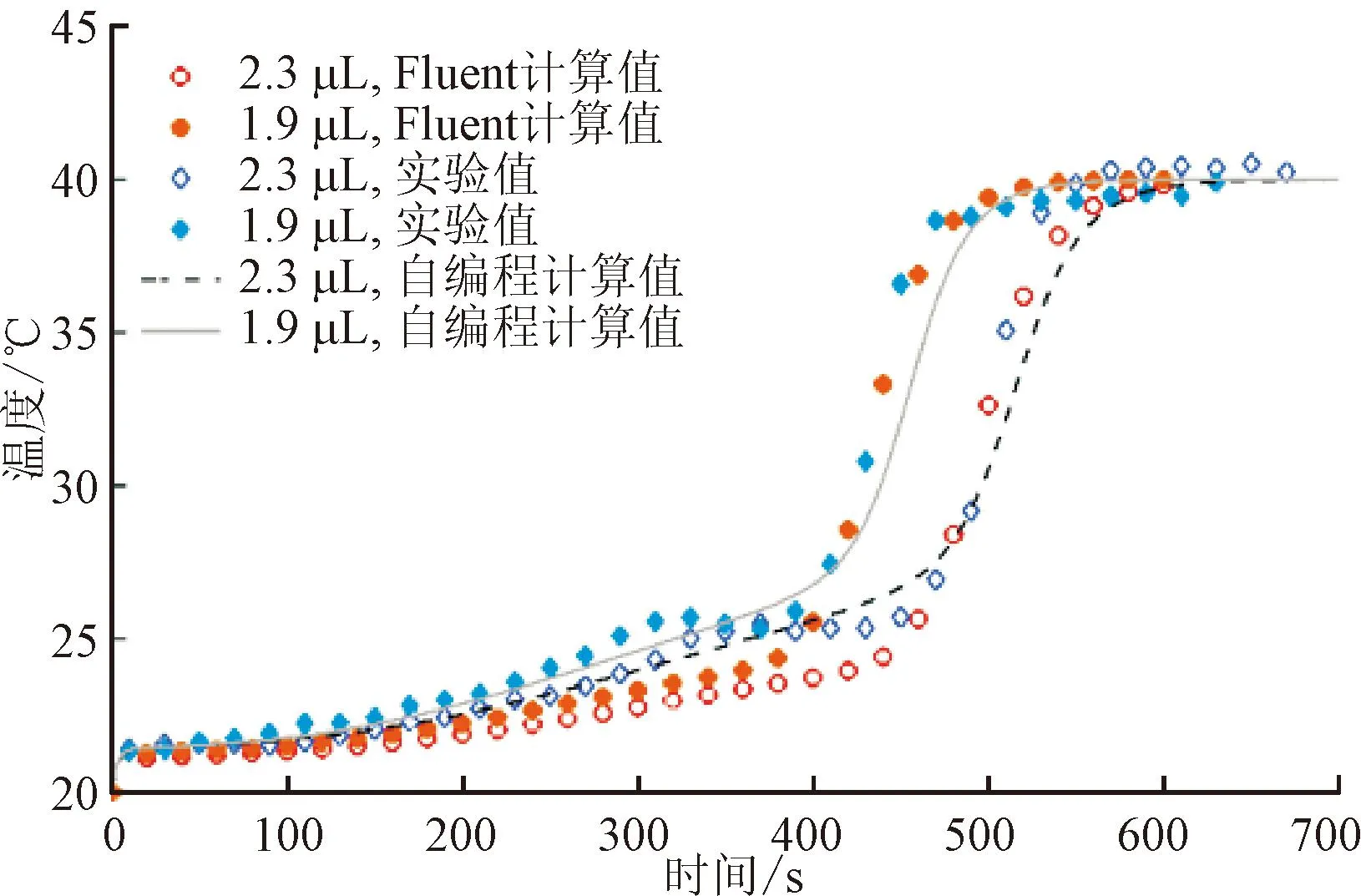
图20 不同初始体积液滴温度计算值与实验值验证

考虑到液滴质量变化在喷雾蒸发数值计算中对液滴轨迹预测的重要性,本文提出的数值模型可用于初始质量分数为10%的NaCl溶液液滴蒸发过程的数值计算。

4 结果与讨论

本文采用悬挂法搭建了单液滴蒸发可视化实验平台,分析了系统振动对液滴质量尤其是质量蒸发率测量的影响,对比了采用不同截止频率的低通滤波对振动信号的消除作用,得到了低频噪声对质量测量的影响显著,并最终选用截止频率为0.01 Hz的低通滤波,大幅减小了质量测量时的振动信号,为含析出性溶质液滴干燥过程中的质量测量提供了可靠思路。

开展了40℃、相对湿度6%的气流环境下,初始质量分数为10%的NaCl溶液的单液滴蒸发实验,记录了初始体积分别为1.9和2.3 μL的液滴蒸发过程中质量、温度、粒径和形貌等蒸发动力学参数。实验数据表明,液滴结晶时已完成蒸发过程80%占比的质量和粒径变化,并伴随表面浓度降低、单位面积蒸发速率增大、液滴小幅温降;直至盐壳完全包覆液滴,此时90%的水分质量完成蒸发,液滴直径和形貌基本不再发生变化,此后温度迅速升高直至蒸发结束达到环境温度。

实验得到了初始质量分数为10%的NaCl溶液液滴在蒸发过程中相对活化能和无量纲粒径随液滴干基自由水含水率的变化关系,建立了相应的REA模型。对比发现,不同初始体积的液滴具有相同的相对活化能和无量纲粒径变化曲线。利用UDF自定义函数将REA模型嵌入Fluent软件进行单液滴蒸发数值模拟,结果表明,液滴初始体积越大,其蒸发中心的水蒸气质量分数越高,尾迹区水蒸气的影响范围越大。Fluent软件计算得到的液滴蒸发过程的质量变化与实验值吻合良好,同时对液滴温度的预测也在误差允许的范围内,验证了本文所提模型应用于盐水喷雾蒸发数值计算的可行性。