融合工况预测的混合动力拖拉机自适应能量管理策略
2023-12-18朱镇曾令新林勇刚陈龙邹荣蔡英凤
朱镇, 曾令新, 林勇刚, 陈龙, 邹荣, 蔡英凤
(1. 江苏大学汽车工程研究院, 212013, 江苏镇江; 2. 浙江大学流体动力与机电系统国家重点实验室, 310027, 杭州; 3. 江苏大学机械工程学院, 212013, 江苏镇江)
“十四五”规划将我国的农业机械提到了极其重要的位置,并明确指出要提升农业机械的核心竞争力。拖拉机是农用动力机械的典型代表,传统大马力拖拉机存在挡位繁多、油耗高及排放性差等问题,不利于环境的保护和可持续发展[1-2]。纯电动拖拉机在短期内受限于电池技术的影响,存在续航里程有限和充电时间过长的问题,不利于拖拉机的持续高功率作业,因此多应用于中小马力的拖拉机。而混合动力拖拉机在原有发动机的基础上,增加了电机作为动力源,在功率需求低时采用纯电动模式,降低排放;在功率需求高时通过电机辅助发动机,使发动机维持在高效率区间内工作,能够降低油耗,被认为是大马力拖拉机实现节能降耗的一个理想方案[3-6]。
在混动拖拉机实际作业过程中,开发高效可行的能量管理策略来协调动力源的动力分配,是实现拖拉机节能减排的关键[7-8]。目前,国内外对混动汽车的能量管理策略研究较多,主要包括基于规则和基于优化2种[9-10]。基于规则的控制策略简单易行,在混动拖拉机中应用较多,诸如功率跟随型策略、恒温器式控制策略等[11-13]。然而,控制规则的制定依赖于设计者的经验,需要通过大量调试获得参数,很难实现最优控制。动态规划算法(DP)是一种全局优化算法,可求解出能量管理问题的最优解。但该算法采用后向求解运算,需预知工况信息,不适合实时应用,多用于策略的对比以及为逻辑规则设计提供参考[14-16]。
等效燃油消耗最小策略(ECMS)是瞬时优化策略的代表,其通过引入“油电等效因子”的概念,将电池电耗等效为发动机油耗,以瞬时总油耗最小为目标,计算出瞬时最优转矩分配组合。该策略计算量适中,适合拖拉机的实时应用[17]。然而,由于适合于某一工况的最优等效因子很难适用于其他工况,因此对电量维持型的混动拖拉机影响较大。针对等效因子工况适应性差的问题,Wang等[18]提出了一种用于混动车辆的模糊自适应ECMS策略,通过考虑电池荷电状态(SOC)偏差与发动机当前转速,建立了等效因子调节的模糊控制器。Rezaei等[19]提出了一种最优等效因子上下边界估计方法,在此基础上设计了一种新的等效因子调整方式。Tian等[20]设计了一种混合算法来识别混动巴士驾驶员的驾驶风格,基于此获得了相应的校正函数,用于对等效因子进行调整。周维等[21]通过分析混动矿用自卸车实际作业工况特点,对SOC参考轨迹进行设计,并结合基于SOC反馈的PI控制器实时调整等效因子。
上述策略均基于SOC反馈、模式识别、历史工况信息等对等效因子进行调整,未考虑未来工况信息对等效因子的影响。因此,本文针对搭载液压机械无级变速器(HMCVT)的混动拖拉机,提出了一种基于拖拉机工况信息预测的等效因子自适应调整方法。首先,利用径向基(RBF)神经网络对拖拉机的作业工况数据进行学习训练,建立RBF神经网络拖拉机工况预测模型;接着,根据拖拉机历史工况的信息预测,得到下一时域的未来工况信息,结合SOC反馈及预测到的未来工况信息,动态调整ECMS策略的等效因子,并将其应用于实际行驶,建立了基于工况预测的等效因子自适应模型;最后,通过仿真实验对控制策略的有效性进行了验证。
1 混合动力拖拉机系统构型
目前,我国传统大马力拖拉机动力传动系统的设计,大部分仍采用柴油机匹配机械式有级变速器的形式,由于纯机械传动无法实现无级变速,为了使发动机的转矩输出特性曲线接近理想状态,因此需要设置繁多的挡位,导致换挡操作繁琐复杂。
本文将混合动力技术与液压机械无级变速传动相结合,设计了一款新型的混合动力机液复合传动装置[22],并应用到大马力拖拉机中。图1给出了混合动力拖拉机动力传动系统的结构原理图。与采用机械有级式变速箱的拖拉机不同,所设计的混合动力拖拉机集成了油电混合双动力源与液压机械复合传动装置,其动力传动系统包括:①发动机部分;②电机部分;③行星齿轮分汇流机构;④液压传动机构;⑤动力输出轴(PTO);⑥输出机构。其中,③和④构成了HMCVT变速器,整个动力传动系统可以看作是油电混合双动力源匹配HMCVT。通过控制离合器C0~C8和制动器B的接合与分离,拖拉机可实现纯发动机驱动、纯电机驱动、混合动力驱动、行车充电及能量回收5种工作模式的切换。
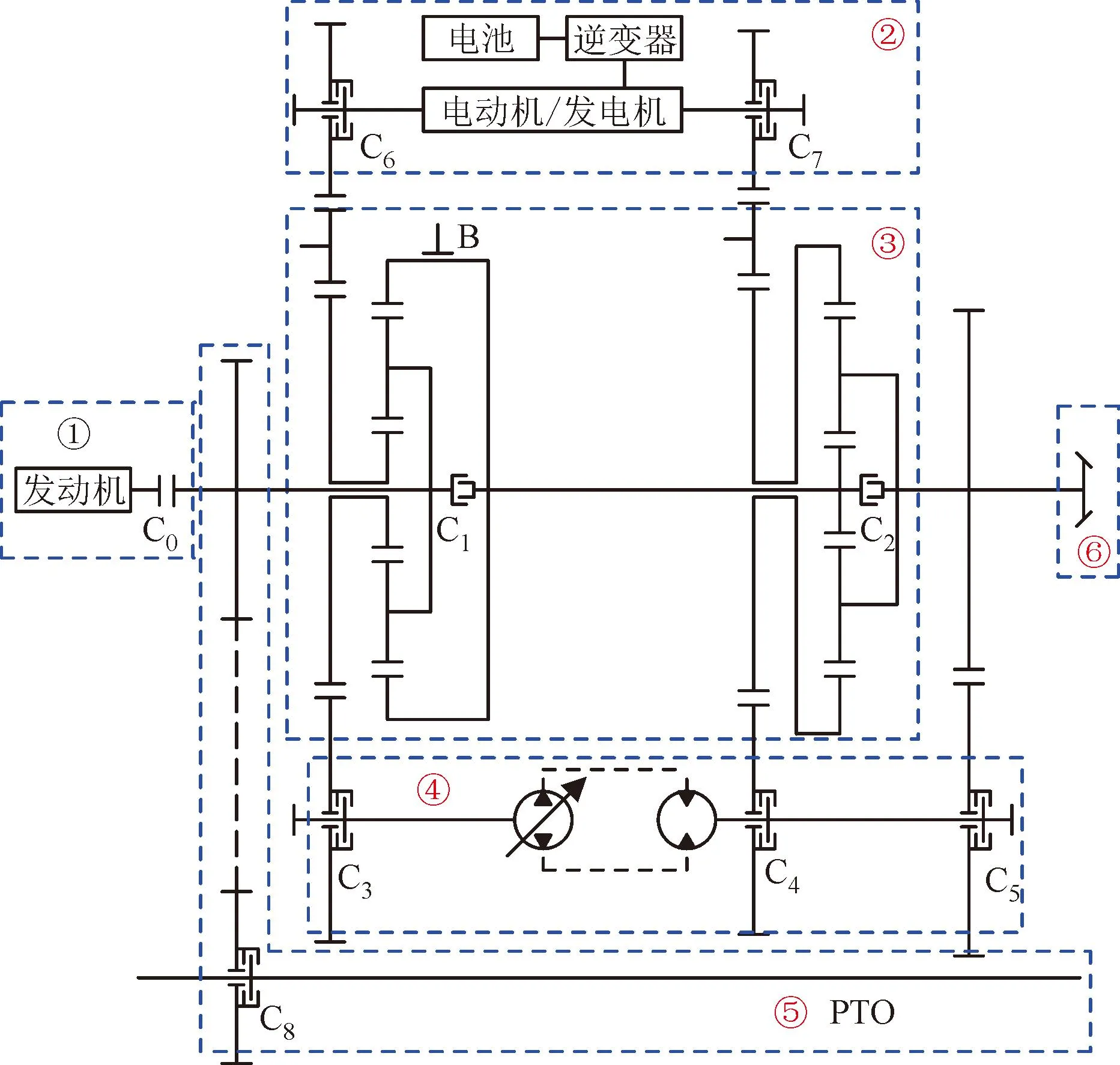
图1 混合动力拖拉机动力传动系统结构原理图
2 动力传动系统建模
2.1 发动机模型
拖拉机通常搭载柴油发动机,因此可采用试验数据建模的方法建立发动机稳态模型,通过数据插值构建发动机比油耗关于发动机转速和转矩的关系曲面。发动机油耗的数学表达式可写为
(1)
式中:Te为发动机输出转矩;ωe为发动机角速度;be为比燃油消耗率;ρ为柴油密度。
2.2 电机模型
通过数据插值构建电机的效率模型,使其可在电动或发电状态下工作。电机的功率可表示为
(2)
式中:Tm为电机输出转矩;ωm为电机角速度;ηm为电机效率,且当Tm>0时为电动机效率,Tm<0时为发电机效率。
2.3 电池模型
电池模型采用Rint模型,即将电池等效为理想电压源Uoc和内阻Rbat串联的模型,电池的输出功率和SOC反馈值可由下式描述
(3)
(4)
式中:Pbat为电池输出功率;Ubat为电池输出电压;Ibat为电池输出电流;Uoc为电池开路电压;Rbat为电池等效内阻;SSOC(t)为t时刻电池的SOC值;SSOC(t0)为电池的SOC初始值;Qbat为电池额定容量。
2.4 变速器模型
对于本文研究的液压机械无级变速器,当发动机工作时,需进行相应的速比匹配。以经济性作为控制目标,通过拟合油门开度与发动机经济性转速数据,可得到拖拉机不同油门开度下最佳经济性转速的计算式,表示如下
ne_opt=-210α4-150α3+810α2+100 0α+750
(5)
(6)
式中:ne_opt为发动机最佳经济性转速;α为油门开度;va为实际车速;ne为发动机转速;rw为拖拉机驱动轮半径;ig为变速器传动比;i0为主减速器传动比;iw为轮边减速器传动比;ε为驱动轮滑转率。
式(6)给出了发动机转速与整机行驶速度的关系,联立式(5)与式(6),可得到液压机械无级变速器经济性速比控制曲面图,如图2所示,其中速比表示变速器的输入转速与输出转速之比。由图可知,随着油门开度和车速的变化,通过查表匹配对应的经济性速比,即可使得发动机运转在最佳经济性工作曲线上。
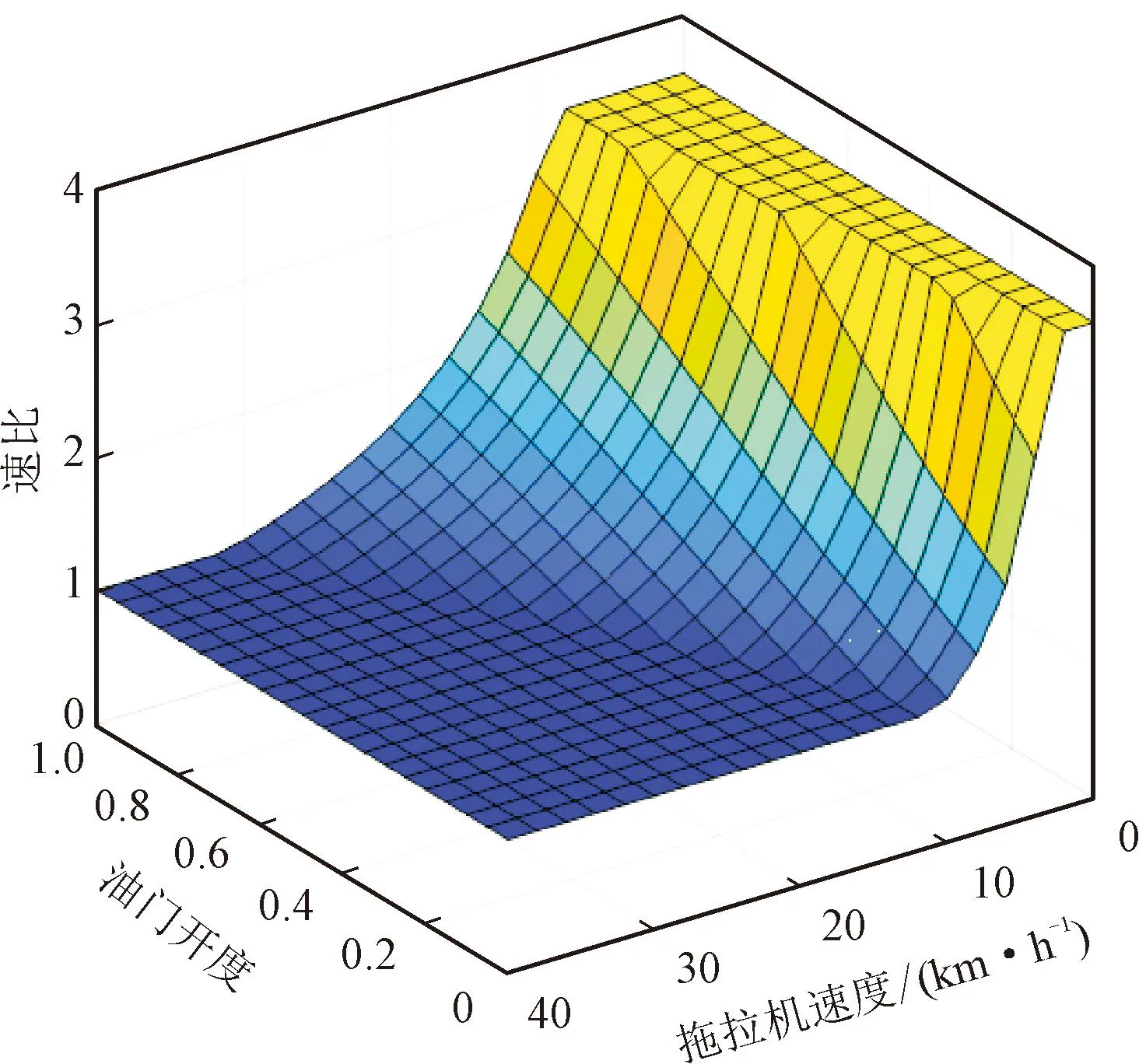
图2 液压机械无级变速器经济性速比控制曲面
2.5 整机纵向动力学模型
搭建的仿真模型主要用于验证车辆能量管理相关控制策略,故仅考虑拖拉机的纵向动力学模型,表示如下
(7)
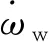
3 拖拉机工况预测模型建立
3.1 拖拉机作业工况分析
一般来说,拖拉机工况可分为道路运输工况和作业工况,其中,作业工况根据所牵引农机具的不同以及动力输出轴(PTO)是否工作,又可分为犁耕、旋耕、施肥等工况;根据负载的大小也可分为轻载、中载及重载作业工况[23]。在进行农场作业时,通常需要拖拉机维持稳定的行驶速度牵引农机具工作,速度改变要缓慢,动力需求稳定,尤其是在特定的农场工作时,工作环境及线路固定,拖拉机只需进行大量定期重复的驾驶循环。因此,只要获得合适的样本数据用于神经网络训练,就能够实现良好的工况信息预测。
德国农业协会(DLG)根据国际标准与法规,制定了PowerMix 测试项目,对拖拉机的油耗、效率及输出功率等进行测试。PowerMix 测试项目开发了14个测试循环工况,包括12个田间作业和2个运输循环,各个测试工况在部分负荷和满负荷下,复现了农用拖拉机典型的田间和运输作业。PowerMix中各测试循环设定的负荷及车速信息如表1所示[24]。
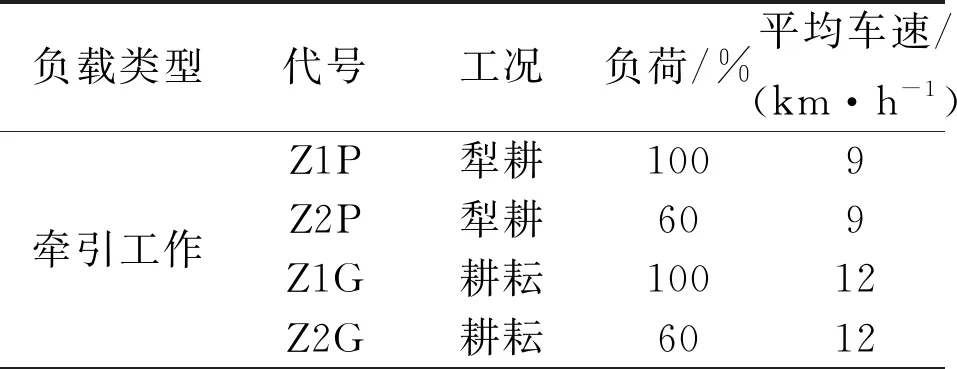
表1 德国农业协会PowerMix测试工况
3.2 基于RBF神经网络车速预测模型的建立
RBF神经网络为单隐层前馈神经网络,被广泛用于非线性化、时间序列预测等领域[25]。图3给出了RBF神经网络的拓扑结构,其中W为权值,b为偏置阈值。不同权值的输入信号先线性相加,再通过偏置阈值进行调整。隐藏层采用高斯函数作为基函数,先对输入序列进行非线性映射变换,再通过输出层线性映射变换得到输入信号所对应的输出。
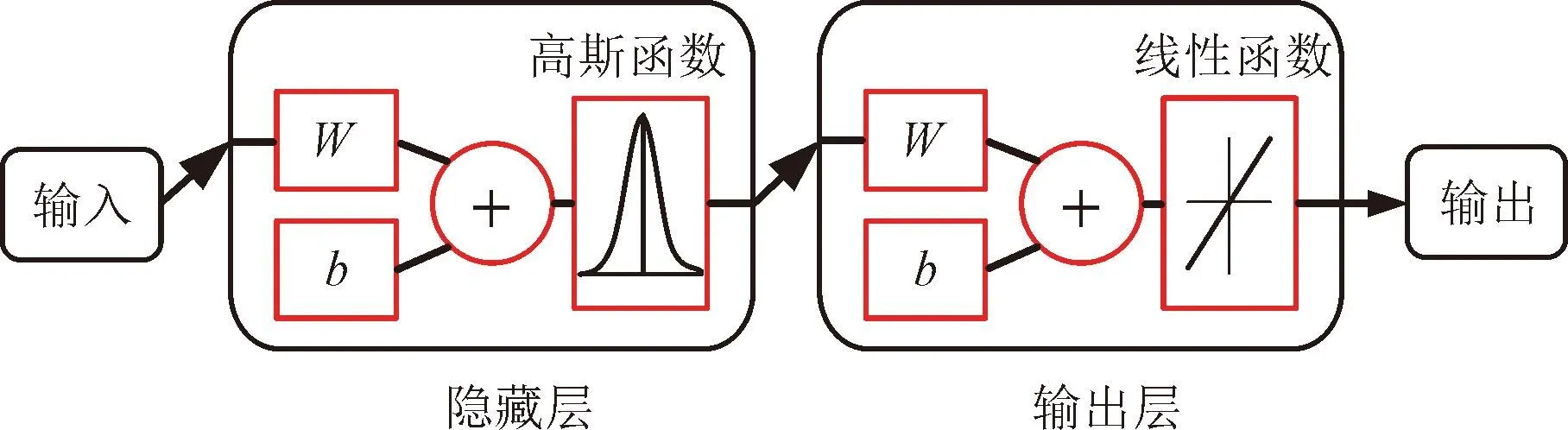
图3 RBF神经网络的拓扑结构
下文以拖拉机工况信息预测中的车速预测为例,将当前时刻k和过去时域Hh的历史车速信息作为神经网络的输入,将预测时域Hp内的预测车速作为神经网络的输出。
考虑到拖拉机工况复杂,负载多变,为了使预测模型在田间作业和道路运输工况下都具备良好的预测精度,提高模型的工况适应性,选取Z1G、Z2P、Z3M、Z3K、Z6MS、Z7PR共6种工况,以及拖拉机现场作业数据组合而成的组合工况作为模型训练样本数据,如图4所示。组合工况全程为6 500 s,综合了3种负载类型,包括拖拉机作业工况中的犁耕、旋耕、耕耘、除草、打捆和施肥等工作循环,能够模拟拖拉机绝大多数的作业工况,因此具有一定的代表性。
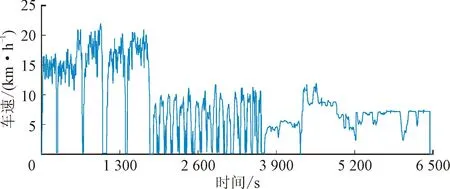
图4 训练样本车速数据
图5为不同预测时域下验证工况的预测效果图,可以看出,基于RBF神经网络车速预测模型得到的车速预测值,能够与实际速度变化趋势保持一致。
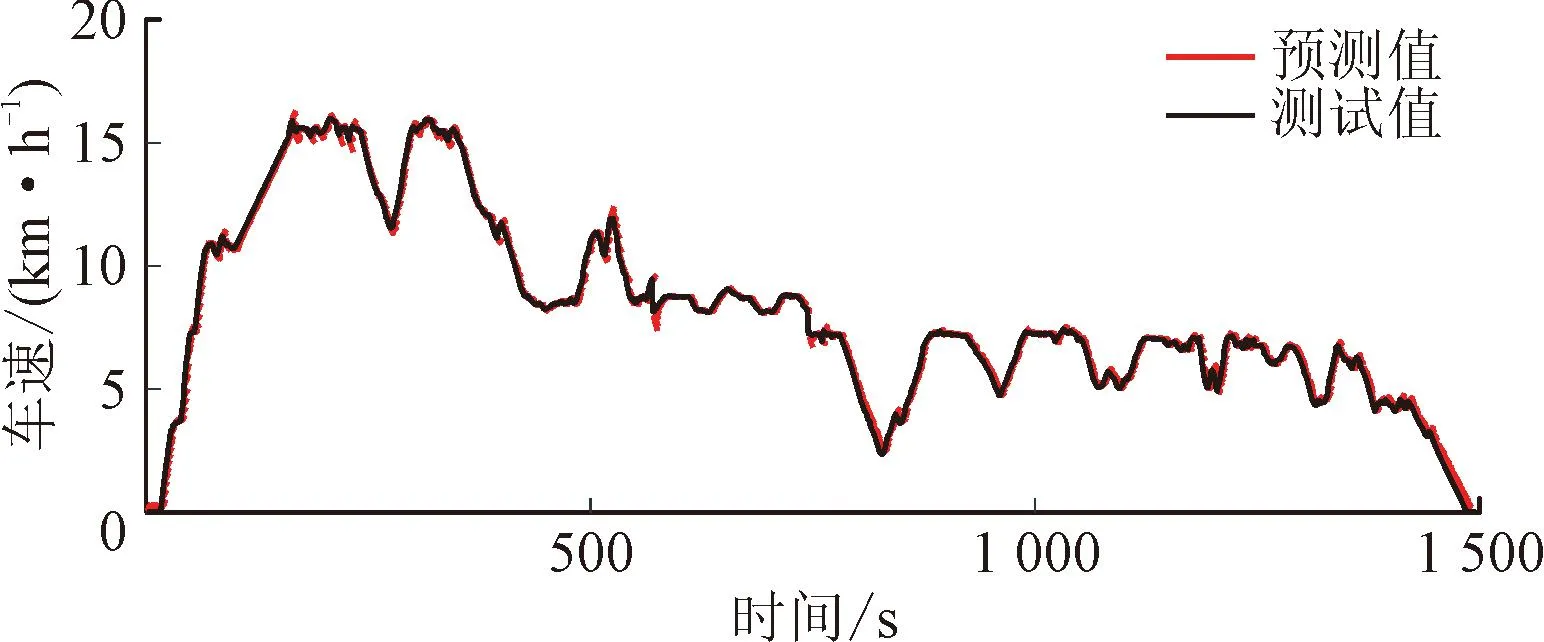
(a)5 s
定义均方根误差ERMSE和平均绝对百分比误差EMAPE,以评价RBF神经网络车速预测模型的准确性。随着预测时长的增加,预测工况的车速信息与实际工况的车速信息误差也随之增加,具体的数据如表2所示。综合考虑预测精度及模型计算量,经过反复调校,选取预测时域长度为10 s,扩散因子为25,隐藏层神经元个数为125,对拖拉机的工况信息进行短期预测。
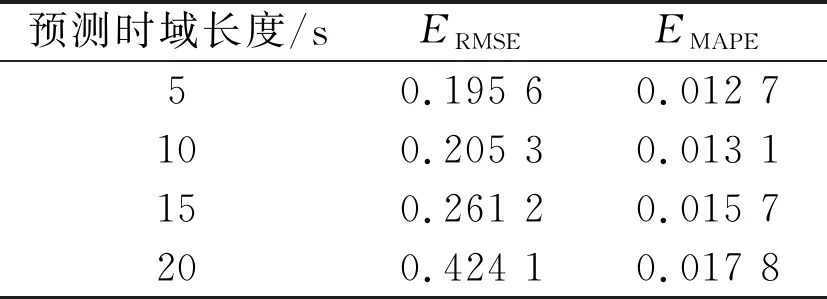
表2 不同预测时域车速信息的误差值
4 拖拉机预测自适应能量管理策略
4.1 等效燃油消耗最小策略(ECMS)
对于非插电式混合动力拖拉机,由于其电池无法通过外部电网进行主动充电,故需要消耗燃油来维持电池SOC 在工况始末的电量稳定。ECMS策略通过引入充放电等效因子,将混动车辆的电耗等效为油耗,并将等效总油耗作为统一指标进行最优控制。以每个瞬时下发动机油耗与电池等效油耗之和最小为目标,在满足相关约束条件的情况下求得最优解。其数学模型可表示如下
(8)
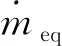
以拖拉机在时域 [t0,tf]内的总燃油消耗最小为控制目标,定义目标函数为
(9)
u(t)=Tm(t)
(10)
式中:状态变量x(t)为电池的SOC值;控制变量u(t)为电机分配的转矩Tm(t)。
对状态变量x(t)求导,可得
(11)
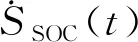
对于电量维持型混动车辆,在时域 [t0,tf]始末应保持电池电量的稳定,即
SSOC(t0)=SSOC(tf)
(12)
而且,系统还需满足以下约束条件
(13)
式中:Te_max、Te_min分别为发动机转矩的上、下限;ωe_max、ωe_min为发动机转速的上、下限;Tm_max、Tm_min为电机转矩的上、下限;ωm_max、ωm_min为电机转速的上、下限;SSOC_H、SSOC_L为电池SOC值的上、下限。
根据庞特里亚金极小值原理,构造瞬时哈密顿函数为
(14)
式中:H为哈密顿函数;λ为拉格朗日算子。
使得哈密顿函数最小的控制变量最优序列uopt(t)可表示为
(15)
结合式(3)和式(11),可将式(14)改写为
(16)
结合式(8)和式(16),油电等效因子可写为
(17)
4.2 预测自适应等效油耗最小策略(PA-ECMS)
传统ECMS策略的等效因子取值固定,工况适应性差,因而导致混动拖拉机在工作时,电池SOC处于不断地波动之中。当设定的等效因子偏小时,电池等效油耗相对较低,能量管理系统偏向于用电,容易导致电池SOC过放。反之,当等效因子偏大时,能量管理系统偏向于用油,导致电池SOC上升从而偏离目标值。为提高拖拉机的燃油经济性与维持电池SOC的稳定性,需对油电等效因子进行动态调整,提高其适应性。
常用的基于电池SOC反馈的等效因子自适应模型可表示为
(18)
ΔSSOC=SSOC_ref-SSOC(t)
(19)
式中:s0为初始等效因子;Kp为比例系数;KI为积分系数;SSOC_ref为SOC参考值;SSOC(t)为SOC实际值。
该模型通过引入PI控制器,根据电池SOC实际值与目标值之间的误差,对等效因子进行实时修正,虽然方法简便,但控制参数的整定需依靠人工经验,且等效因子每时每刻都在调整,修正时间过短且限制电池SOC的行程在目标SOC附近,不利于电能得到充分有效的利用。
本文提出的融合拖拉机工况预测的PA-ECMS策略,能根据神经网络预测得到的未来工况信息对等效因子进行调整,等效因子离散自适应的规律可描述如下。基于预测的拖拉机工况信息,对等效因子进行自适应调节,得到
(20)
式中:s(k)为k时刻的等效因子;s(k+1)为k+1时刻的等效因子;T为等效因子离散自适应的时间周期;ψ[(k+1)T]为未来车速的变化对等效因子的影响,可表示为
ψ[(k+1)T]=KSOCδ
(21)
式中:KSOC为常数;δ=VPS,i/VPA,i,其中VPS,i为预测时域i内的车速标准差,VPA,i为预测时域i内的车速平均值,两者又可分别表示为
(22)
(23)
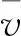
未来工况预测时域区内车速标准差与均值的比值δ,反映了单位均值上的车速数据离散程度,可用来描述未来有限时域内拖拉机行驶状态的变化趋势。若比值δ在下一个区间偏大,则说明车辆较上一区间有频繁加减速的趋势,车辆需求功率较大,需相应增大等效因子;若偏小,则表示车速变化平稳缓慢,需要减小等效因子。因此,根据比值δ的大小对等效因子进行实时调整,可满足不断变化的工况需求。PA-ECMS能量管理控制策略的框架如图6所示。
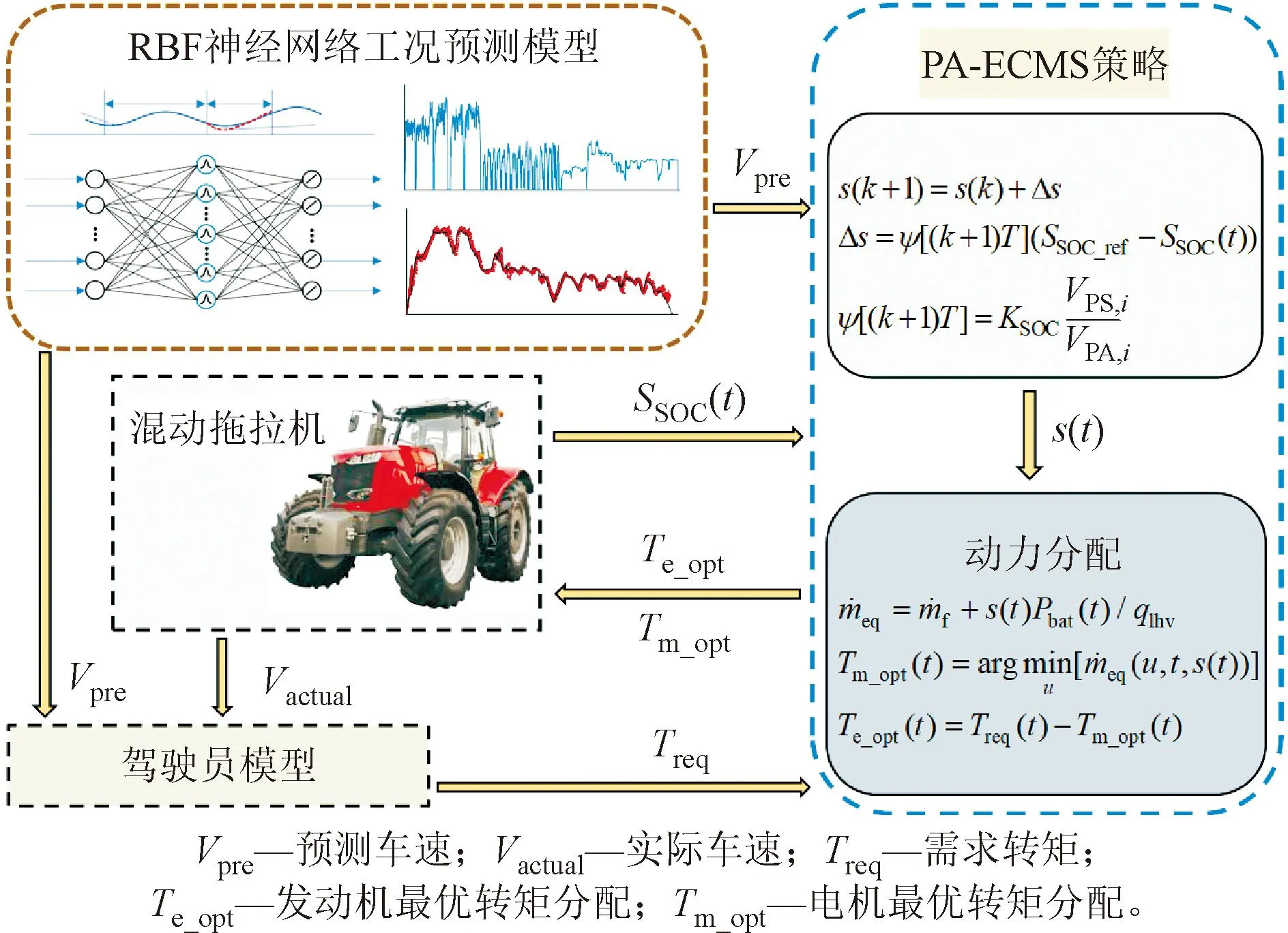
图6 PA-ECMS能量管理控制策略框架
5 仿真分析
5.1 仿真模型构建
整车动力传动系统的主要部件参数如表3所示。采用SimulationX软件,搭建混动拖拉机的整机物理模型;采用Matlab/Simulink软件,搭建控制策略和工况预测模型;通过SimulationX软件调用编译器生成的可执行文件,最终实现联合仿真。
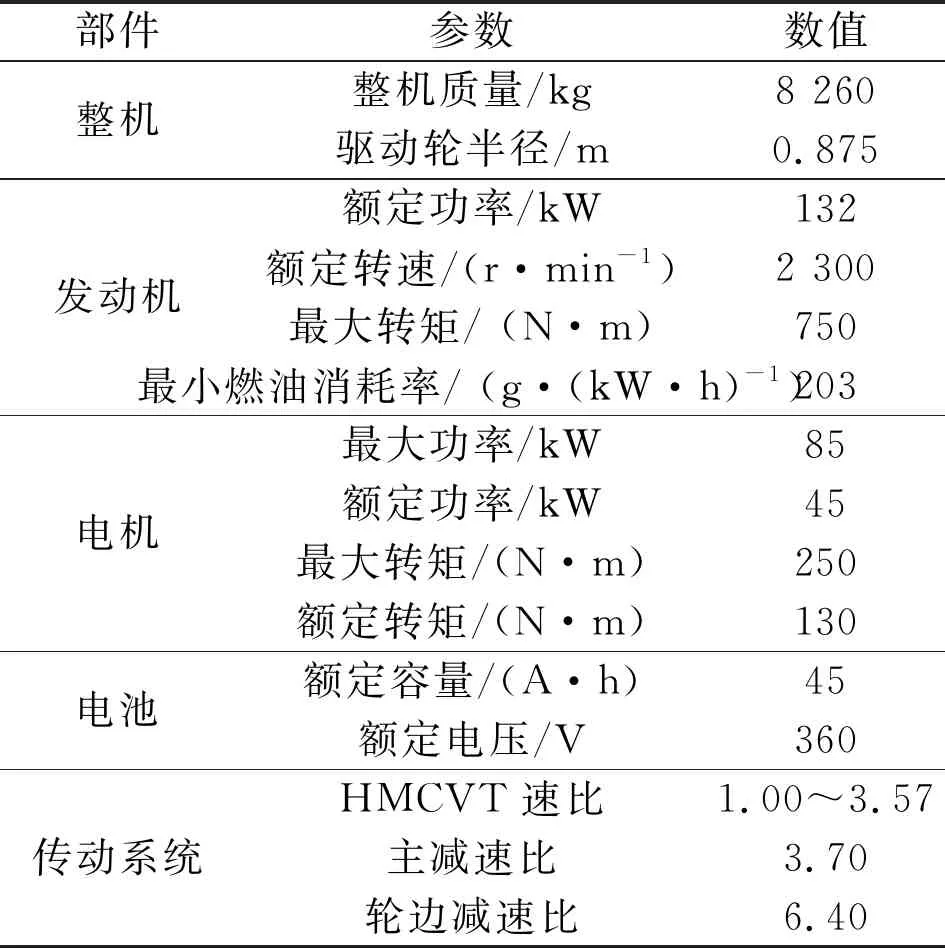
表3 动力传动系统主要部件参数
5.2 仿真工况构建
犁耕作业工况是拖拉机最具代表性的工况之一,根据美国环保署(EPA)公布的农用拖拉机工况数据,建立本文所研究混动拖拉机的犁耕工况,并将其作为联合仿真的工况,如图7所示。犁耕工况时间持续600 s,其中,平均牵引阻力为36.60 kN,平均作业车速为8.86 km/h。
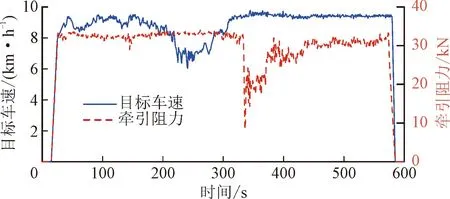
图7 本文所研究混动拖拉机的犁耕工况
5.3 模型预测精度分析
图8为犁耕工况下预测时域为10 s时,采用基于RBF神经网络的拖拉机工况预测模型得到的车速预测结果。由图可见,预测结果与拖拉机真实行驶车速存在偏差,误差在工况始末以及200~250 s之间较大,这是由于加速度变化剧烈所导致的。但总体上,预测车速的变化趋势与实际车速的变化趋势基本保持一致,且其ERMSE及EMAPE分别为0.195 6和0.016 7,能够满足预测精度需求。
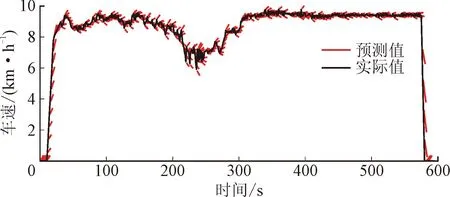
(a)车速预测值与实际值对比
5.4 节油性验证
图9对比了分别采用传统ECMS策略、仅基于SOC反馈的自适应等效燃油消耗最小策略(A-ECMS)以及本文所提PA-ECMS控制策略时,发动机及电机的功率优化分配、电池SOC轨迹变化、等效因子调整轨迹和油耗情况。从发动机和电机的功率分配可以看出,A-ECMS和PA-ECMS策略下,电机功率波动的幅度相较于传统ECMS策略更大,表明对电机的利用更为充分。在220~260 s时,由于车速下降导致整机需求功率变小,传统ECMS策略需通过启用电机分担需求功率,此时处于电机和发动机共同驱动状态;而A-ECMS和PA-ECMS策略则采用发动机提供整机需求功率,同时通过给电机充电,维持发动机在高效区域工作,从而有效地降低了油耗。传统ECMS策略的等效因子固定,整个工况内均为初始值2.75,但该值并非犁耕工况下的最优等效因子,因此导致SOC终值与电量维持的目标值偏离较大。在330~380 s时,由于载荷波动导致整机需求功率下降,此时电池SOC偏离设定的电量维持值,A-ECMS和PA-ECMS策略可通过提升电机的输出功率,保持与发动机共同驱动。对等效因子进行自适应调整后可以看出,A-ECMS和PA-ECMS策略下等效因子SOC轨迹在SOC目标值附近波动更加频繁,且PA-ECMS策略在提供SOC反馈的基础上还能对未来工况进行预测。然而,与A-ECMS策略在每一时刻连续对等效因子进行调整不同,PA-ECMS策略对等效因子的调整是周期性的,故对电能的利用更为充分,波动幅度相较于A-ECMS策略更大,表明其具有更为优异的电量维持性能。
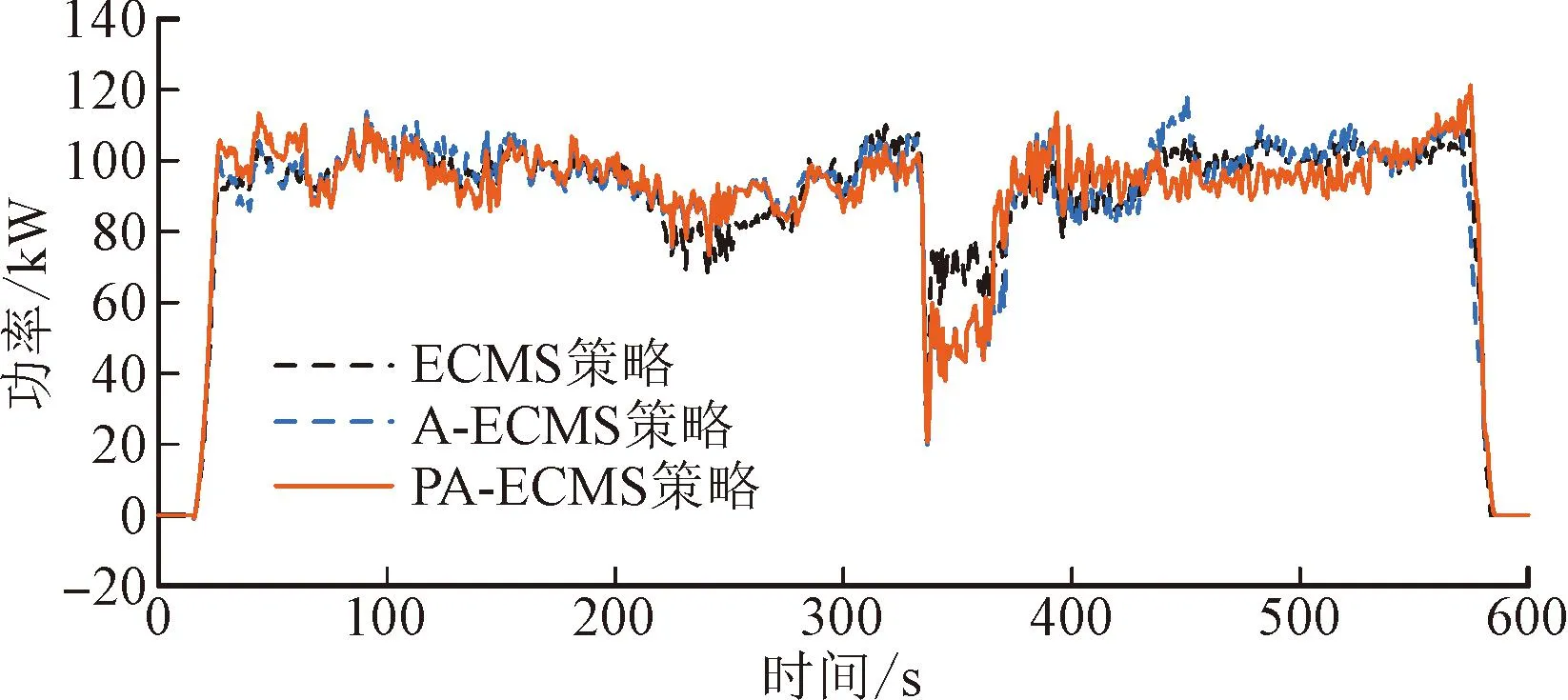
(a)发动机功率
上述3种策略在工况结束时,电池SOC值与目标值均仍存在偏差,故应对仿真结束时得到的燃油消耗量进行修正,以消除SOC变化对油耗的影响。通过添加一个取决于SOC变化的拟合系数σ来修正燃油消耗,修正后的油耗可表示为
mf0=mf-σΔSSOC
(24)
式中:mf0为达到电量维持值,即电池SOC值为0时的燃油消耗量;mf为仿真结束时的燃油消耗量;σ为ΔSSOC转换为对应燃油量的拟合系数。
表4给出了油耗校正后,3种不同控制策略下混动拖拉机在某个犁耕工况下的电池SOC值和油耗对比。可以看出,A-ECMS和PA-ECMS策略在犁耕工况下的节油效果均优于ECMS策略,节油率分别为3.85%和6.30%,体现了等效因子随着工况变化的自适应调整对整机油耗的影响。在一个犁耕工况结束后,PA-ECMS策略的节油率仅高于A-ECMS策略2.45%,二者在油耗方面相差不大。相较于初始设置的电量维持值60%,A-ECMS和PA-ECMS策略的电池SOC终值分别偏离了0.51%和0.13%,表明PA-ECMS策略下电池SOC电量的维持性能更为优越,这是因为PA-ECMS策略可以提前预测未来工况信息。然而,预测模型的误差始终是无法避免的,后续仍需不断提升预测模型的精度,以进一步提升节油率。
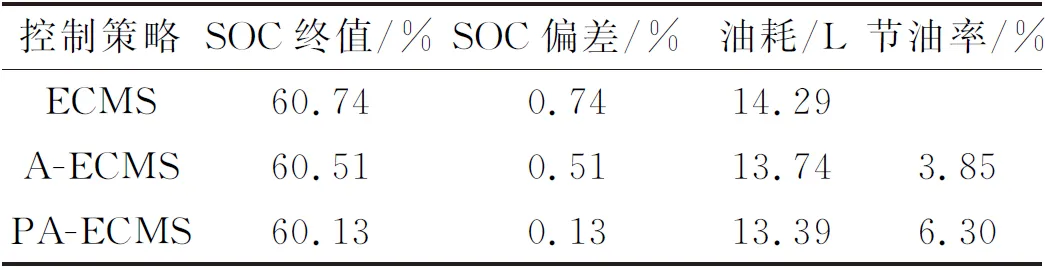
表4 不同控制策略下的电池SOC值和油耗对比
在犁耕工况下,PA-ECMS策略相较于其他两种策略的发动机实时工作点分布对比如图10所示。
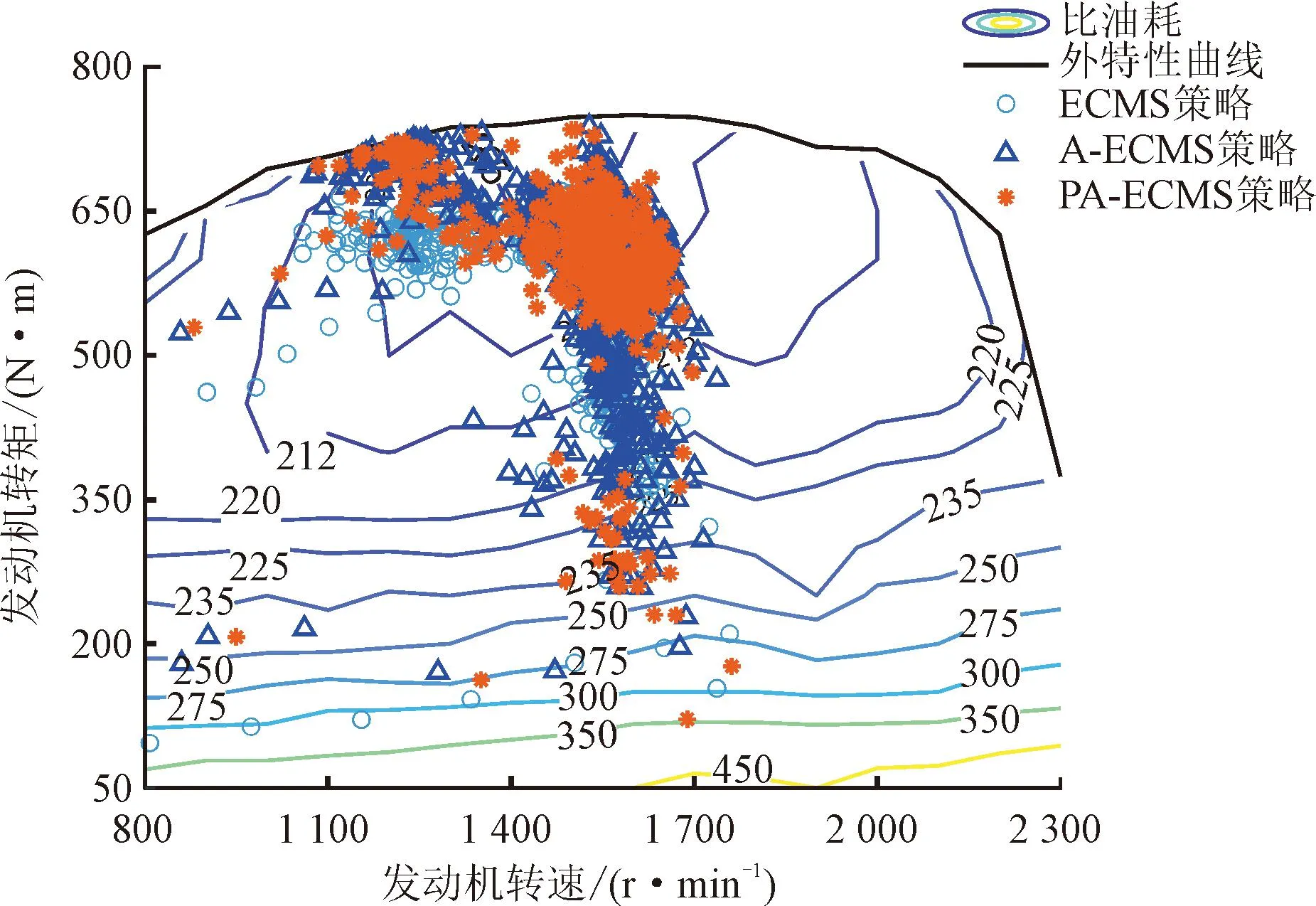
图10 不同控制策略下的犁耕工况发动机工作点分布对比
由图10可见,通过预测未来工况信息对等效因子进行动态调整后,发动机工作点更为密集地分布在高功率、高效率区域,表明发动机的负荷率得到了有效提升,这也是PA-ECMS策略的节油性优于ECMS和A-ECMS策略的主要原因。
6 结 论
本文以一款搭载混合动力液压机械无级变速总成的大马力拖拉机为研究对象,结合拖拉机的工况信息,提出了一种融合工况预测的PA-ECMS策略,并在一个犁耕工况下进行了仿真验证,得到的主要结论如下。
(1)基于RBF神经网络,对拖拉机的历史工况数据集进行训练学习,找到输入与输出之间的映射关系,建立了满足预测精度要求的RBF神经网络拖拉机工况预测模型,得到犁耕工况下预测时域为10 s 时的均方根误差及平均绝对百分比误差,分别为0.195 6和0.016 7。
(2)PA-ECMS策略相较于仅基于SOC反馈的A-ECMS策略和传统ECMS策略,节油率分别为2.45%与6.30%。电池电量维持方面,3种策略在工况结束时的电池SOC值相较于初始值,分别偏离了0.13%、0.51%和0.74%。
(3)所提出的PA-ECMS策略工况适应性较好,原因在于其等效因子通过SOC反馈信息和RBF神经网络模型预测得到的拖拉机未来工况信息,能够自适应地进行动态调整。该策略不仅提高了混合动力拖拉机燃油经济性,还在工况结束时体现了更好的电池SOC电量维持性能。
