一种考虑微凸体接触角分布的结合面侧接触分形模型
2023-12-18王世军刘鑫范凌松崔圣奇李鹏阳
王世军, 刘鑫, 范凌松, 崔圣奇, 李鹏阳
(西安理工大学机械与精密仪器工程学院, 710048, 西安)
机械结构中两个相互接触的表面称为结合面。宏观上是光滑平整的零件表面,微观上总是粗糙不平的。两个零件表面的接触,微观上都是两个粗糙表面的接触,接触性质并不是两个光滑表面的接触性质。结合面的形貌特征和材料特性决定了结合面的接触特性。如何从接触面的微观形貌入手构建准确的接触模型,对于研究结合面的接触特性[1]乃至分析机械整机的静态和动态性能,都有重要意义。
在结合面的接触问题研究中,学者大多将结合面简化成粗糙表面和刚性平面的接触,相当于峰-峰接触,此时两微凸体的接触角度为0°。双粗糙表面微观上微凸体之间除了正接触,大多为肩-肩接触,接触角度范围在0°~90°之间[2]。
针对侧接触问题,Sepehri等[3]将微凸体定义为椭球体,研究了倾斜接触力在法线和切线方向上的分量,建立了SF统计模型。Gorbatikh等[4]提出了一个接触角度分布函数,并用统计方法研究了微凸体之间的侧向接触性质,但是没有给出这个角度分布函数的理论依据。Misra等[5]通过引入一个方位函数来模拟接触角和各向异性表面,利用微力学模型来研究倾斜接触微凸体的滑动行为,并将剪切方向与法向的接触刚度耦合起来,建立了考虑接触方向分布和微滑移特性的侧接触统计模型。高志强等[6]引入文献 [4]的接触角度函数,建立了考虑微凸体斜接触和相互作用的结合面接触刚度及阻尼模型。Jamshidi等[7]根据微凸体接触时的穿透量来界定接触状态,同时对Misra的接触角度函数进行修正,由此建立了接触界面法向载荷与剪切力耦合的HJ模型。文献 [4-7]在研究斜接触问题时虽然给出了接触角的分布函数,但对其分布规律的来源和依据没有明确说明。范凌松等[8-9]研究了粗糙表面上相邻微凸体的水平距离,发现水平距离遵循高斯分布规律,建立了包含法向和切向接触特性的FLS模型,研究了相关轮廓统计参数及相互作用对结合面接触刚度的影响。
利用分形模型研究侧接触问题时,孙见君等[10]根据微凸体斜接触时上下两轮廓的空间坐标与接触角的联系,建立了双粗糙面的侧接触分形模型,分析了表面形貌参数、接触压力对孔隙度和实际接触面积的影响,该模型采用的接触角函数是由空间几何关系获得,与水平距离无关。Zhang等[11]基于MB模型和侧接触理论建立了考虑接触角分布的ZK改进分形模型,该模型假定接触角的范围在0°~45°之间,通过给定接触面积与接触角的函数关系来研究接触角对接触刚度的影响,该模型忽略了水平距离的存在,且假定的角度范围与实际不符。以上模型都未对接触角的理论来源加以研究。
本文基于分形理论研究粗糙表面上相邻微凸体之间的高度差和水平距离的分布规律,采用分形方法描述相邻微凸体之间的距离分布,结合相邻微凸体之间高度差的分形规律,遵循微凸体峰高与水平距离的统一性,得到粗糙表面上微凸体侧向接触时接触角的分布函数,同时考虑弹塑性边界条件的连续性及域扩展因子对真实接触面积的影响,以此为根据建立考虑微凸体水平距离和接触角分布的侧接触分形模型。通过仿真分析探究了相关接触参数对结合面接触刚度的影响。
1 微凸体中心水平距离分布规律
针对45钢磨削加工表面,利用DCM3D莱卡显微镜分别沿着轮廓水平方向按1 μm分辨率和高度方向上按0.25 μm分辨率进行采样,根据采样数据绘制的三维表面轮廓图如图1所示。
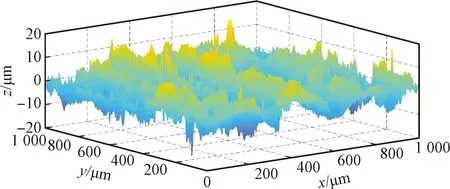
图1 磨削表面三维轮廓
本文统一按“三点峰”的定义来获取一组轮廓上n个峰值点的水平坐标xi,i取1~n,以第1个峰为基准,之后每个峰相对上一个峰的坐标差定义为水平距离si,同理把后续每个峰与前一个峰的高度差的绝对值定义为峰的高度差hi,如图2所示。
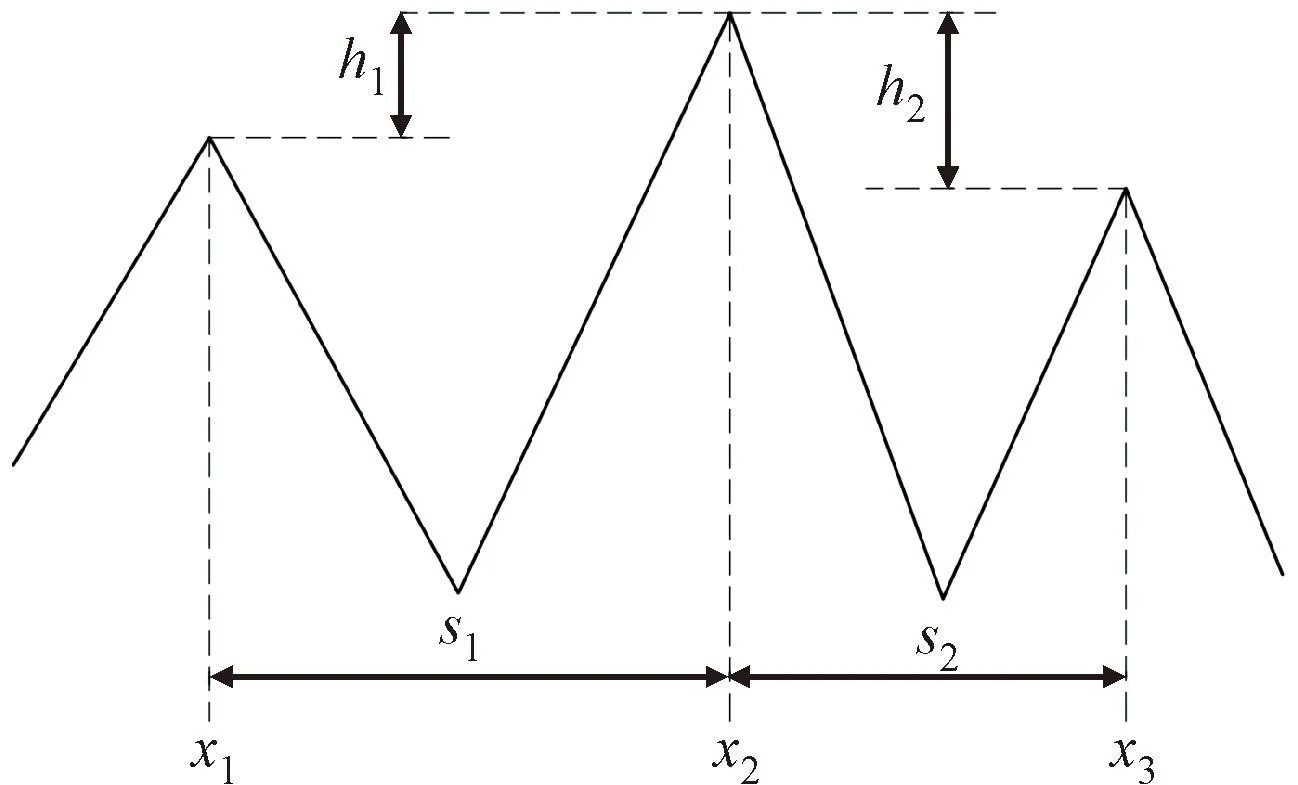
图2 微凸体水平和峰高距离定义
针对磨削试样按照顺纹理方向提取多组断面的二维轮廓数据,分别统计各组轮廓不同间隔下的水平距离数据,拟合出的轮廓曲线如图3所示。
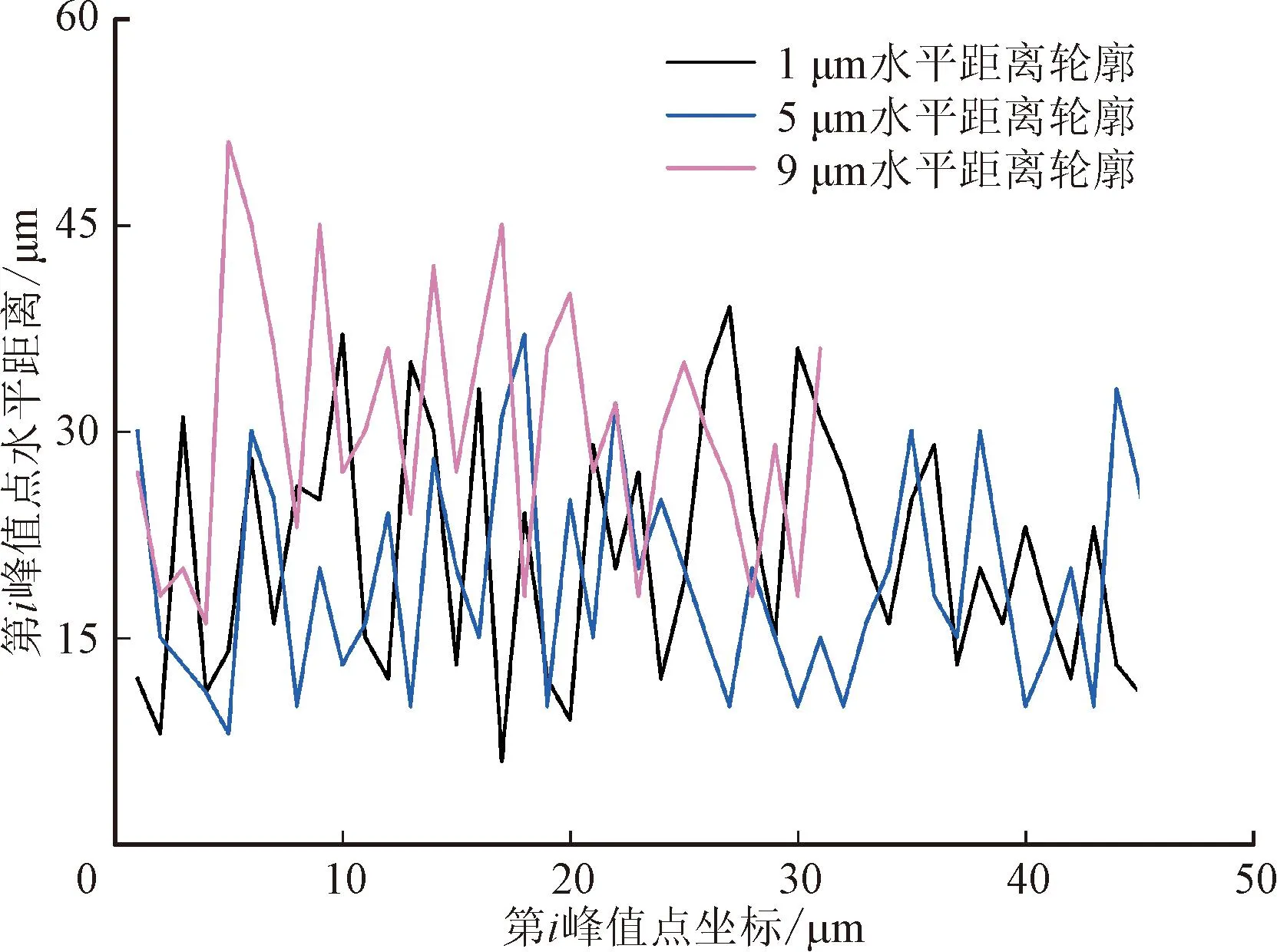
图3 不同间隔水平距离轮廓
已有研究表明,磨削加工得到的机械表面在微观结构上微凸体的接触类型主要为侧向接触[10]。本文采用PSD法来获取上述轮廓的分形参数,首先利用MATLAB编写程序,得到对数坐标下的功率谱密度函数,利用最小二乘法线性拟合求出其分形参数,从而验证水平距离是否具有分形规律。
对文献 [12]中的PSD函数左右各取对数
lnP(ω)=(2D-5)lnω+(2D-2)lnG-ln(2lnγ)
(1)
式中:D为分形维数;G为分形尺度参数;ω为空间截止频率;γ为尺度参数,通常取1.5。PSD曲线斜率为2D-5,截距为(2D-2)lnG-ln(2lnγ)。按照该方法对图3中的水平距离轮廓数据进行计算。间隔1 μm下水平距离轮廓的PSD曲线和最小二乘法拟合的曲线如图4所示。
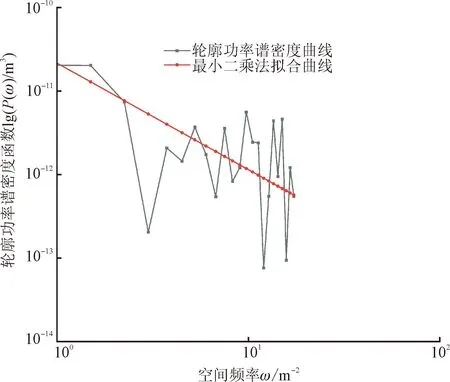
图4 1 μm间隔水平距离功率谱密度曲线
按照相同方法分析相邻微凸体峰的高度差轮廓,峰的高度差满足分形规律。根据三点峰两组表面轮廓数据计算得到的分形参数如表1所示,分析表1中数据可以看出,不同采样间隔下三点峰水平轮廓和峰的高度差轮廓的斜率k在 [-3,-1]之间[13],证明本文按三点峰定义的两种轮廓满足分形规律,因此可以利用二者的分形规律建立法向和切向刚度模型。
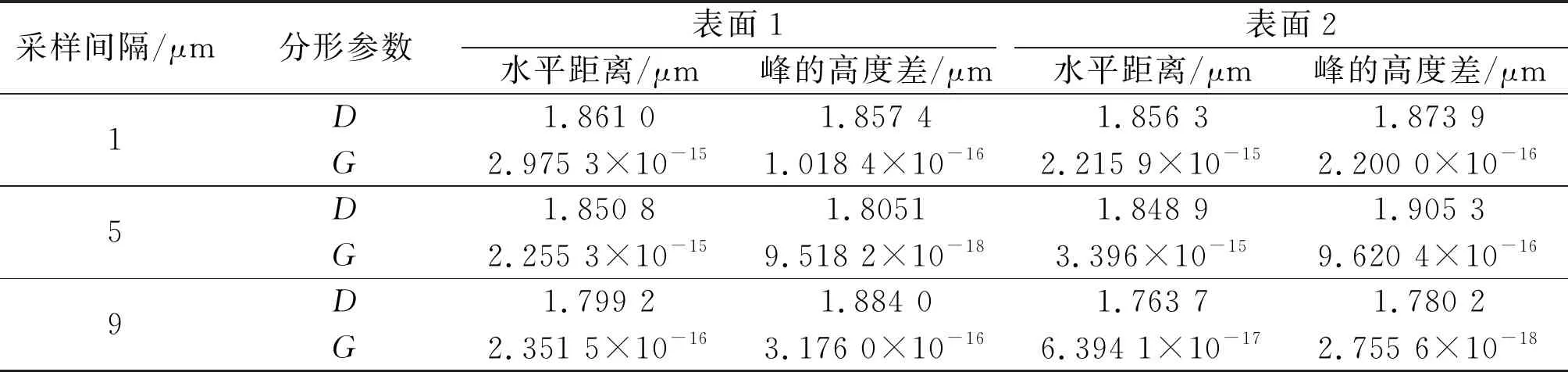
表1 轮廓分形参数统计
2 单对微凸体侧接触模型
微凸体在法向力P和切向力T作用下发生侧接触时,其接触过程如图5所示,S、R分别为微凸体的高度、曲率半径,下标1、2代表上、下两微凸体,下标n、τ代表法线和切线方向,结合面的平均间距用d表示,微凸体中心水平距离和接触角度分别用r、θ表示。在Z′OX′坐标系中,法向接触力P沿上下微凸体接触面的法线和切线方向可分解为Pn、Pτ,同理切向力T可分解为Tn、Tτ,上下微凸体在Z′轴方向的形变量为ωZ′,X′轴方向位移量为ζX′。在ZOX坐标系中,Z轴方向变形为ωZ,X轴方向位移为ζ。
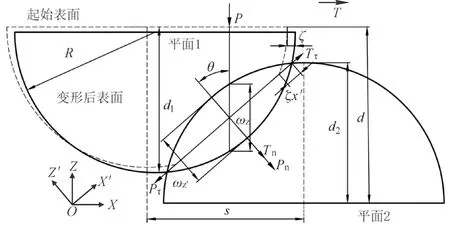
图5 微凸体肩对肩接触
单对微凸体在发生侧接触时存在以下几何关系
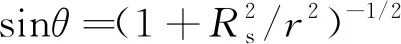
(2)
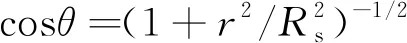
(3)
δ=S1+S2-d-r2/2Rs
(4)
式中Rs=R1+R2[14]。
根据侧接触受力关系可得
P=PZ′cosθ-TX′sinθ
(5)
T=PZ′sinθ+TX′cosθ
(6)
式中:PZ′=TX′tan(α+θ),其中PZ′、TX′分别代表Z′、X′方向所受的合力。
2.1 弹性接触变形阶段
单对微凸体发生侧接触时,实质上为两个半球体在侧臂上的接触,此时两球体存在一个接触角θ,定义单对微凸体接触时Z′方向上的变形量为ωZ′,由Weierstrass-Mandelbrot分形函数可得单个微凸体的变形及等效曲率半径[15]
ωZ′=2GD-1(lnγ)0.5(2r′)2-D
(7)
R=r′D/[24-DGD-1(lnγ)0.5]
(8)
式中:r′为微凸体的截断半径。
根据图中几何关系可以得到微凸体在Z′方向上的变形
ωZ′=ωZcosθ+ζsinθ
(9)
当微凸体达到临界变形接触状态时,在Z′方向上变形量为[16]
δZ′ec=(πKH/2E)2R
(10)
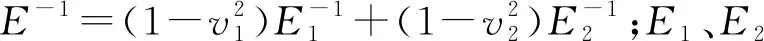
联立式(7)、(8)和(10)可得微凸体在Z′方向上的临界接触面积
(11)
微接触点的截面积a的面积分布函数[18]为
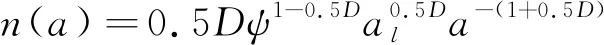
(12)
式中:al为最大微接触点的截断面积;ψ为与分形维数D有关的域扩展因子,且近似满足ψ=1.549D-1.253+1.069。
当微凸体在Z′方向上变形量ωZ′<ωZ′ec时,此时微凸体为完全弹性接触状态,依据赫兹接触理论及文献 [19],可得微凸体弹性接触阶段的法向合力,切向合力与变形量ωZ′关系[19]如下
pe=4ER1/2b3/2c1/3
(13)
te=4ER1/2b3/2c2/3
(14)
b=ωZcosθ+ζsinθ
(15)
c1=[cosθ-sinθ/tan(θ+α)]
(16)
c2=[sinθ+cosθ/tan(θ+α)]
(17)
弹性阶段,两微凸体之间的法向接触刚度
kne=dpe/dω=2ER0.5b0.5c1cosθ
(18)
切向接触刚度为
kτe=dte/dζ=2ER0.5b0.5c2sinθ
(19)
2.2 弹塑性变形阶段
上下微凸体发生侧接触时在弹塑性阶段的临界变形范围为ωZ′ec≤ωZ′≤110ωZ′ec。根据文献 [20],在ZOX坐标系中,微凸体在弹塑性区法向合力、切向合力与变形量ωZ′之间的关系分别为
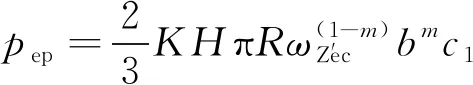
(20)
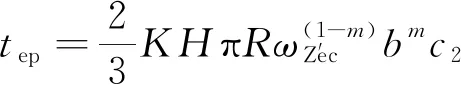
(21)
在ZOX坐标系中,微凸体的法向接触刚度、切向接触刚度可表示为
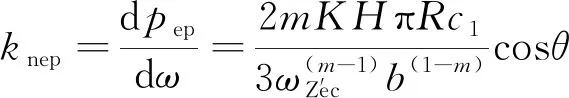
(22)
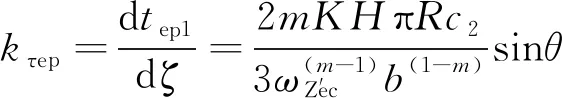
(23)
式中:m=ln(330/K)/ln(110)。
2.3 塑性变形阶段
当微凸体在Z′方向上变形量ωZ′≥110ωZ′ec时,微凸体进入完全塑性接触状态,此时微凸体的平均接触载荷与两接触材料中较软一方的硬度相等。完全塑性变形阶段Z方向上的法向合力与变形量ωZ′的关系[21]如下
pp=2πHRbc1
(24)
此时法向接触刚度
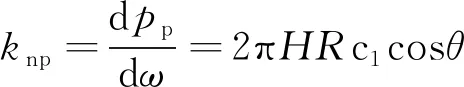
(25)
3 结合面的接触刚度分形模型
由于水平距离和峰的高度差都具有分形规律,因此可用W-M函数来表征相邻微凸体的轮廓
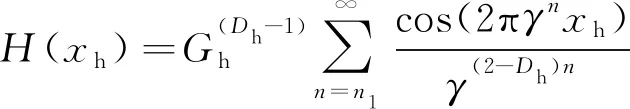
(26)
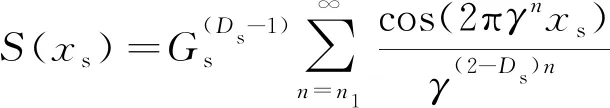
(27)
式中:Dh,s、Gh,s分别为分形维数、分形尺度参数;γn为表征粗糙表面的频谱;n为频率指数;xs为水平距离;xh为峰-峰相对距离。
在坐标系中,接触角θ与两个轮廓的正切值有关,因此接触角的分布函数为
θ(xs,xh)=arctan[H(xh)/S(xs)]
(28)
根据接触角几何关系及式(28)可得微凸体接触角的概率密度函数
f(θ)=
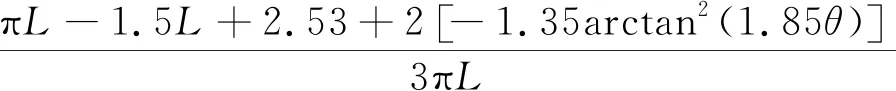
(29)
式中:θ为肩对肩接触角,范围为0°~90°;L为接触表面加载次数。
根据式(29)拟合出分布函数曲线,分布规律如图6所示,可以发现:接触角度函数值随着接触角θ的增加而减小;随着加载次数增加,接触面逐渐压平,接触角度函数值变化逐渐缓慢。
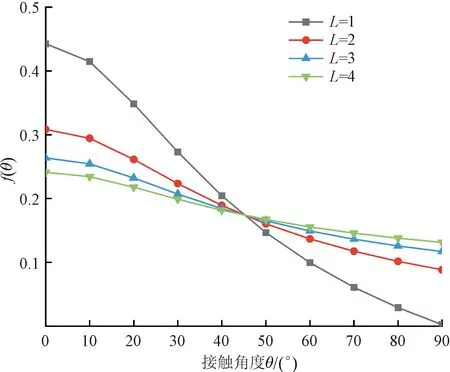
图6 侧接触角度分布规律
微凸体发生弹性、弹塑性和全塑性变形的3个区域面积之和构成了结合面的真实接触面积[20]
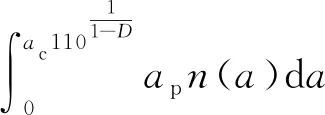
(30)
将式(12)代入式(30),可得
amax=Ar(2-D)Ar/[Dψ(1-0.5D)]
(31)
根据文献 [21]及式(7)、(8)、(10)、(12)和(31),结合面无量纲法向接触载荷P*可表示为
((2-D)/D)0.5Df(θ)dadθ
(32)
无量纲切向接触载荷T*为
a[(0.5D-1)+(1-D)m]c2f(θ)dadθ
(33)
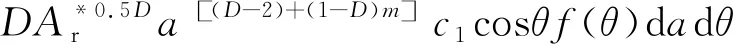
(34)
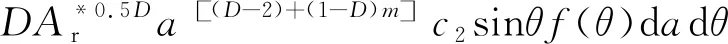
(35)
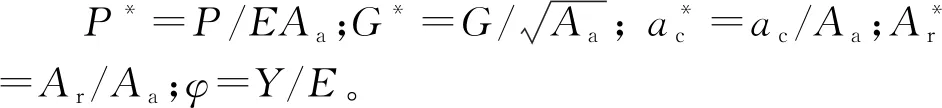
4 结果与分析
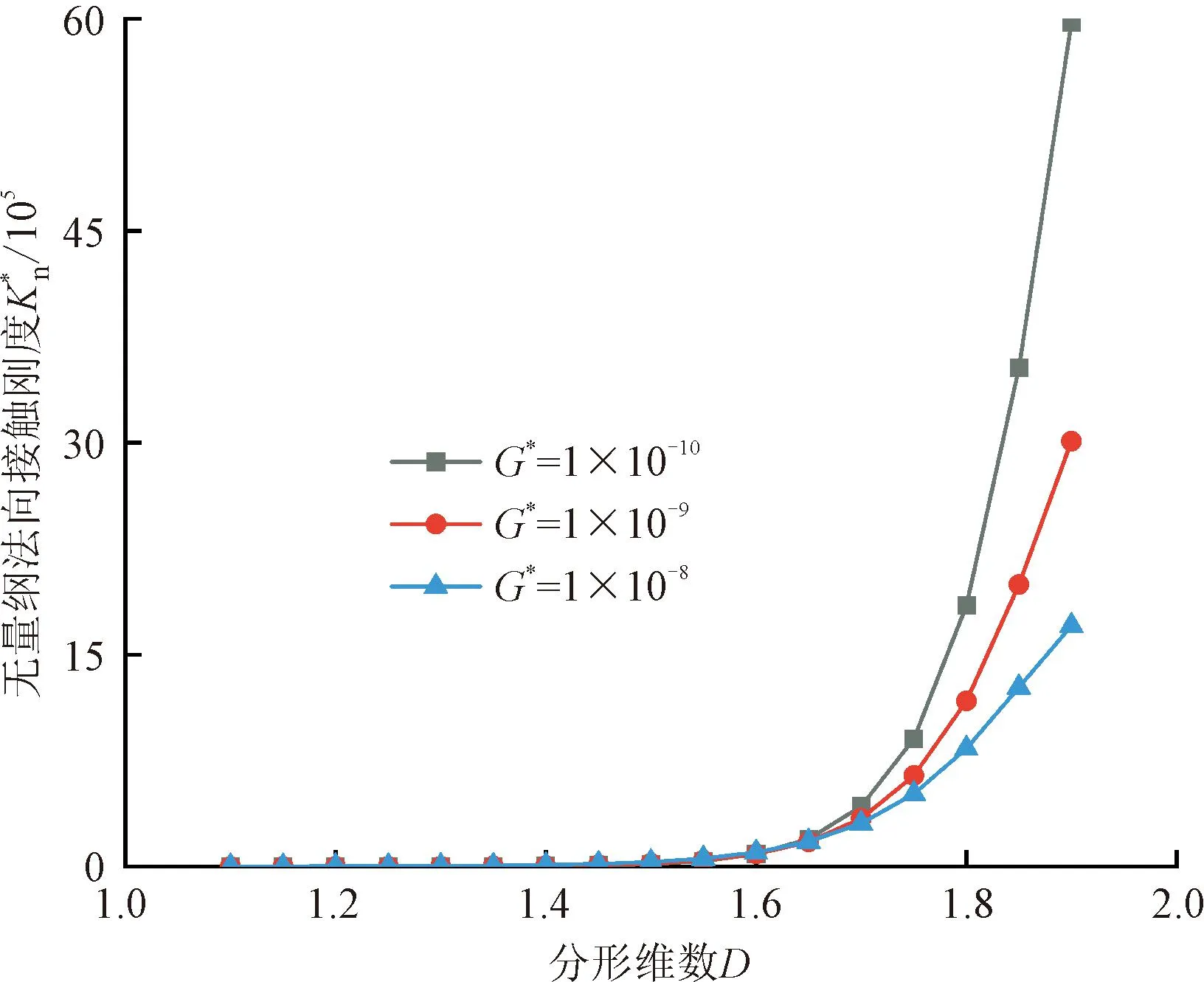
(a)D对的影响
对上述仿真曲线进行分析可得如下结果。
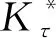
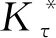
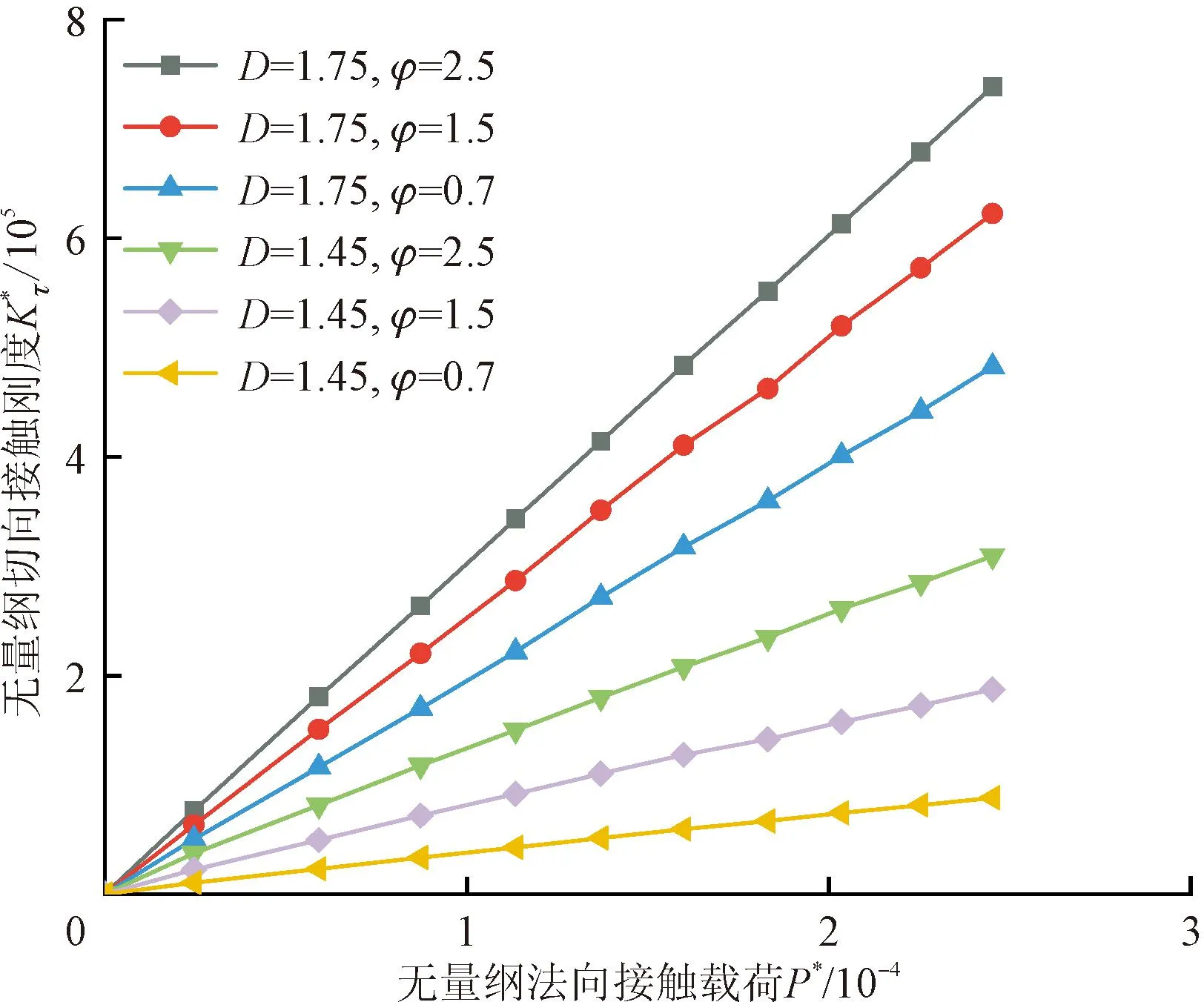
图8 材料参数对切向接触刚度的影响
(3)接触参数对真实接触面积的影响。真实接触面积随法向载荷的变化曲线如图9所示,可知D、塑性指数φ的增大会使真实接触面积不断变大,D越大,表面轮廓越趋近于光滑,而φ越大微凸体越不易发生塑性变形,从而使临界的接触面积不断变小,而真实接触面积的占比不断变大。因此,改善分形维数和塑性指数有助于提高真实接触面积。
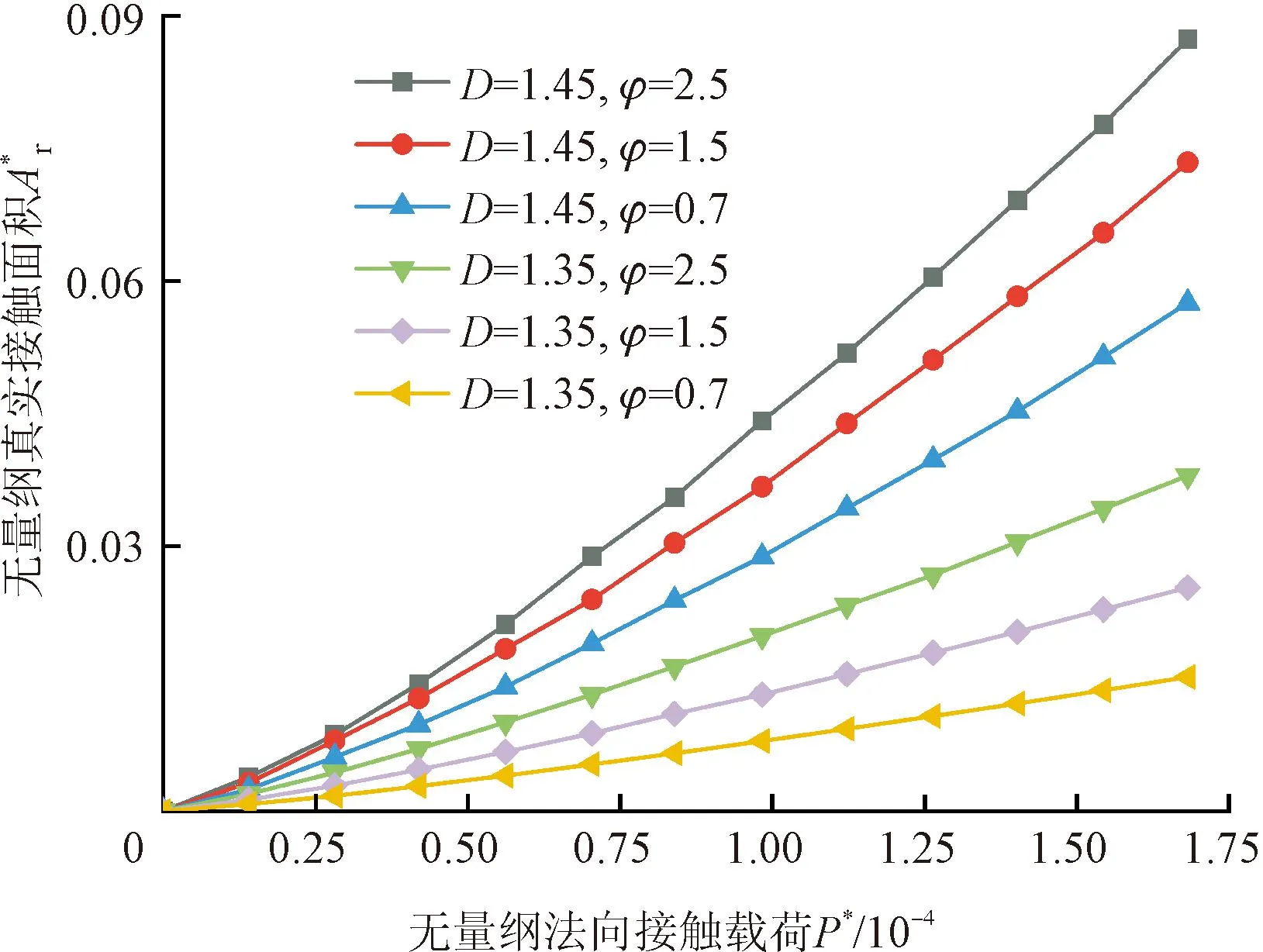
图9 接触参数对真实接触面积的影响
(4)法向载荷系数的影响。图10为结合面接触刚度与法向载荷系数的变化关系。h分别取2~50时,无量纲法向和切向接触刚度均随着法向载荷系数h的增大而增大,随着分形尺度参数G*的增大而减小。固定分形尺度参数G*时,保持结合面法向载荷P不变,h的增大意味着结合面切向接触载荷T减小,则接触面抵抗切向变形的能力增强,从而结合面法向和切向接触刚度都会增大。
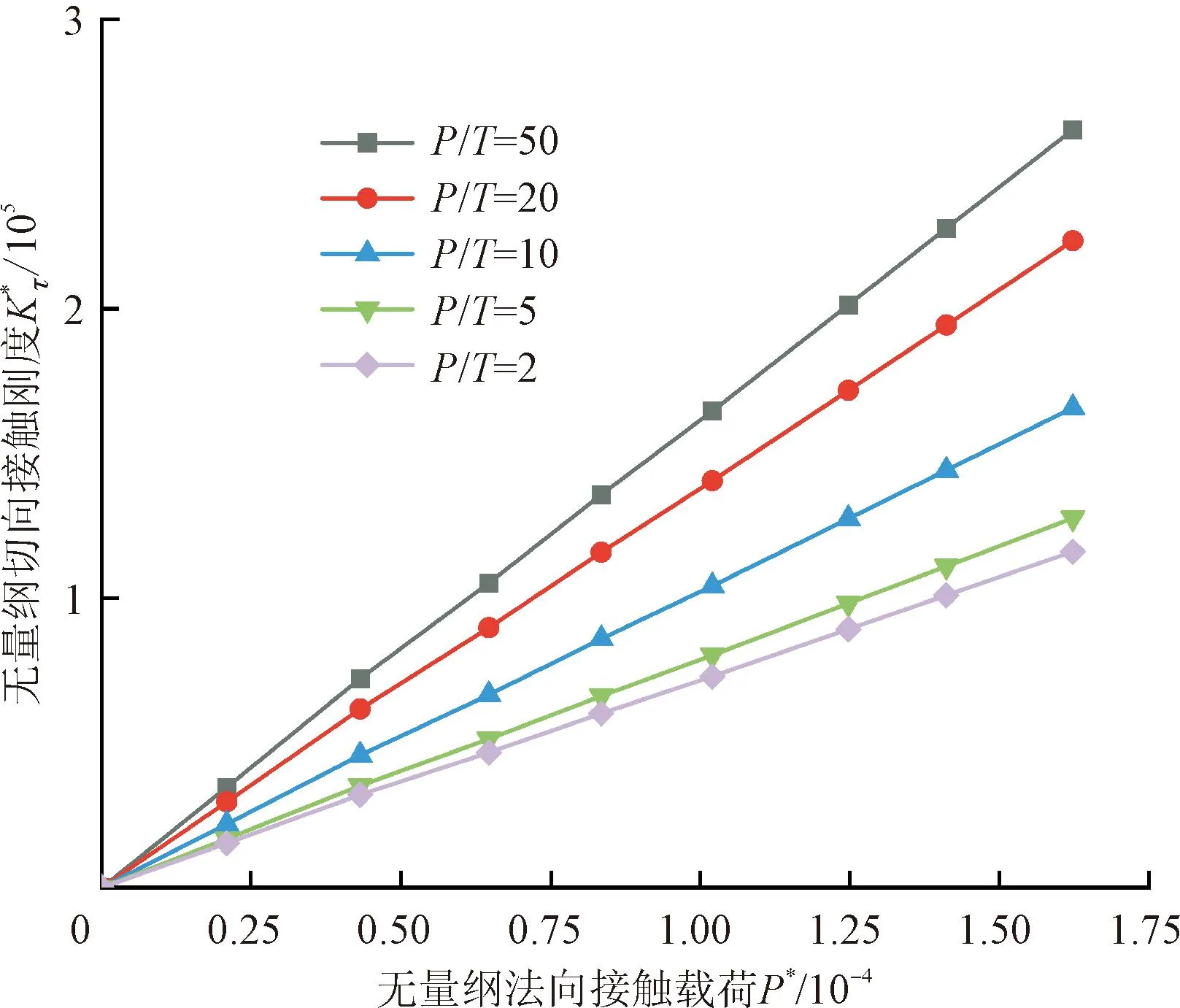
与h的变化曲线
(5)接触方式的影响。图11为两种模型的接触刚度和真实面积随法向载荷变化的曲线。其中LZT模型[16]的接触类型为正接触,本文模型则考虑了侧接触,给定相同的无量纲法向载荷,新模型的接触刚度和真实接触面积小于LZT模型,根据图6及文献 [6]的研究可知,正接触的接触角度函数值相比侧接触较大,而LZT模型忽略了侧接触的影响,导致该模型的刚度偏高。
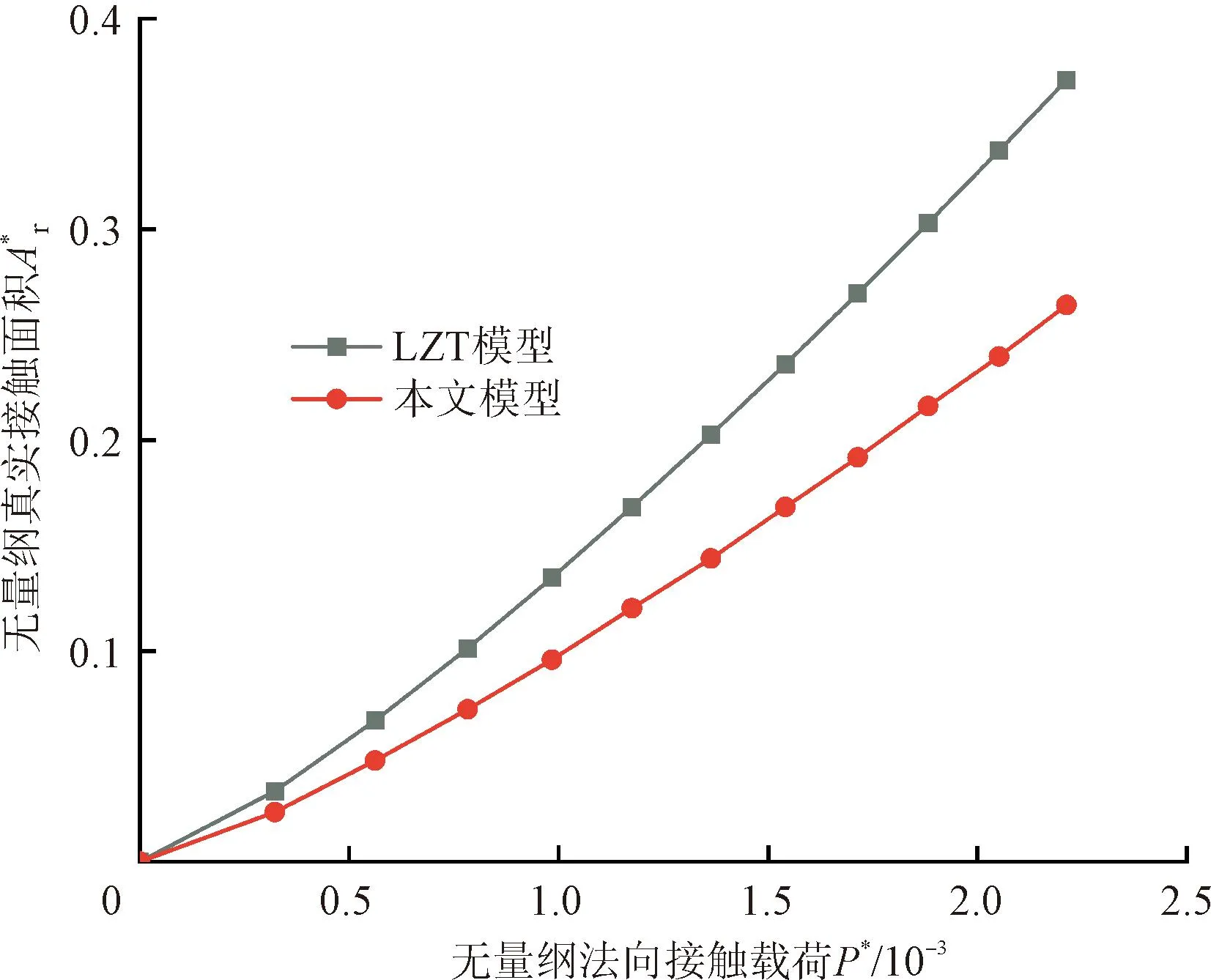
(a)真实接触面积
5 有限元仿真与试验验证
采用文献 [9]的试验装置来验证本文提出的侧接触分形模型,结合部由两半环及螺栓构成,半环材料均为45钢,半环接触面为磨削表面,两材料的厚度和半径分别为35、275 mm,表面经丙酮清洗,其他材料参数如表2所示。

表2 整环材料参数
截取部分二维轮廓数据,经过PSD功率谱计算可得D=1.425,G=2.928×10-10m,半环联结面上每个螺栓能承受的最大拧紧力矩为80 N·m。本文采用锤击法获得整环试验装置的振型和固有频率,同时建立整机的有限元接触模型并进行模态分析,综合比较试验与有限元模型的结果。
由于包含结合部的机械结构的接触刚度具有非线性的特征,因此需要将包含接触的非线性模型线性化,再通过有限元模态分析进行线性化求解,具体过程如下[21]:基于虚拟材料法建立整环有限元接触模型;通过静力分析获得接触层在工作静载荷下的刚度;如果整环工作时的载荷波动远小于静载荷,可认为整环在工作时接触层的刚度保持不变,即用静力分析获得的接触层刚度建立整环的线性模型,将非线性模型线性化;通过整环线性模型的模态分析获得结合部的振型及固有频率。
依据式(34)、(35)及LZT模型计算的法向、切向接触刚度数据可得虚拟材料层的非线性接触参数,试样和整环有限元模型的材料参数一致。采用APDL语言将虚拟接触层的材料参数[22]、非线性接触参数写入整环有限元接触模型,整环模型共使用80 798个SOLID185单元,其中结合部虚拟接触层单元有1 858个,厚度为1 mm[23],如图12所示。
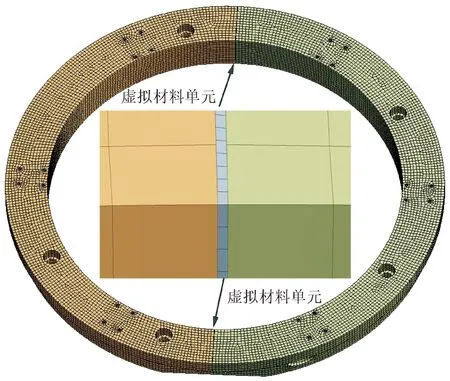
图12 整环有限元模型
对上述有限元接触模型进行静力分析可以求得虚拟接触层在静载荷下的接触刚度,再利用APDL语言将虚拟接触层刚度代入模态分析,可得各阶固有频率及振型[22-27]。本文计算了法向面压为0.6 MPa时本文模型与LZT模型[16]的有限元模态,图13为本文的试验与有限元前3阶振型汇总,表3为3种模型不同面压下的模态分析结果。
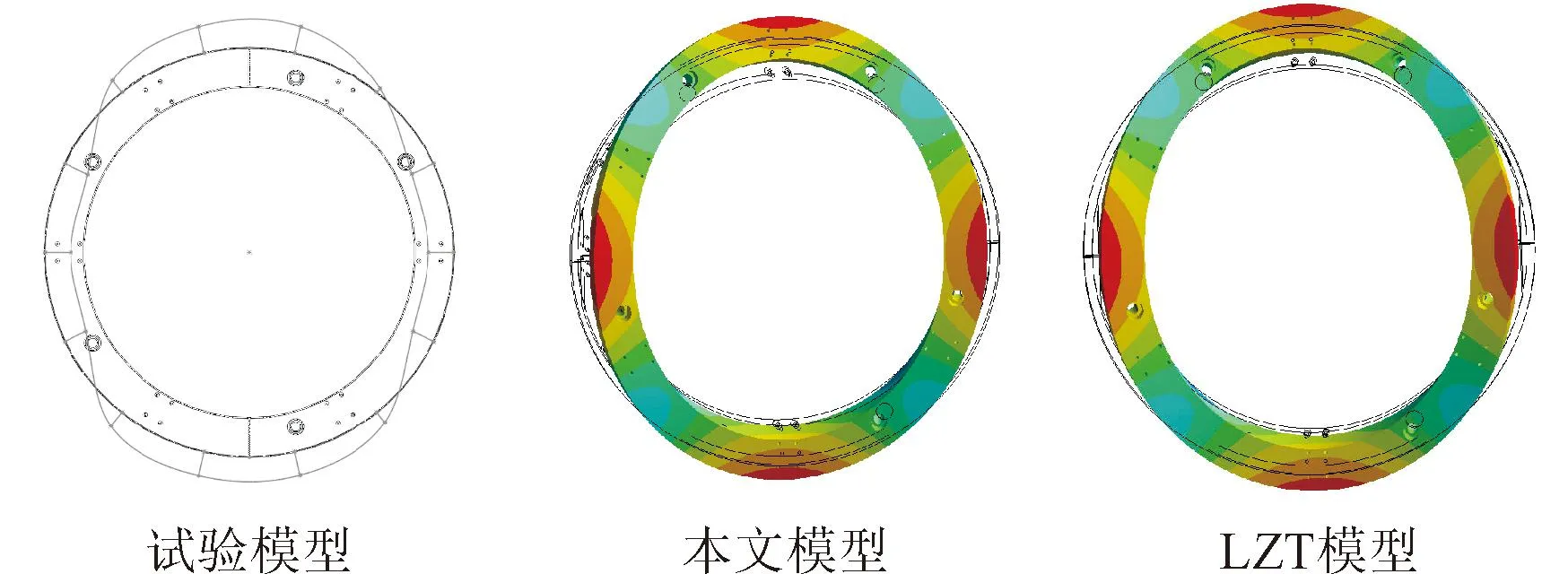
(a)第一阶
由表3可知LZT模型的最大相对误差绝对值为8.12%,而本文模型为4.32%,与LZT模型相比精度提高了46.80%。利用本文研究的接触角分布函数及侧接触建模方法来计算有限元模型的固有频率和振型,与试验结果相比误差最小,本文模型的精度得到了验证。
6 结 论
(1)磨削表面微凸体大多为肩并肩的侧接触,本文对三点峰水平距离和峰的高度差进行定义,经过分析发现,二者近似满足分形规律,首次建立了考虑微凸体水平距离分布的结合面接触刚度分形模型。
(2)本文构造了微凸体水平距离和峰的高度差的分布函数,根据侧接触相对关系确定了接触角θ的分布函数,与Gorbatikh模型的角度分布函数趋势相同,接触角θ和加载次数是影响接触角度分布规律的主要原因。
(3)本文建立的有限元模型与试验结果最大相对误差绝对值为4.32%,说明考虑侧接触水平距离及接触角影响的接触刚度分形模型更加贴近磨削结合面的真实接触特性,可为研究侧接触问题提供新的思路。
