采用Peng-Robinson方程和体积平移的脂肪酸甲酯液相密度预测
2023-12-18蔡凌霄张钰婧王晓坡
蔡凌霄, 张钰婧, 王晓坡
(西安交通大学能源与动力工程学院, 710049, 西安)
脂肪酸酯(包括脂肪酸甲酯和脂肪酸乙酯)是一类由脂肪酸和醇类通过酯化反应生成的有机化合物,是可再生替代燃料生物柴油的主要成分。为了更好地表征生物柴油燃料特性并优化发动机喷嘴等的构型及尺寸,掌握不同链长的脂肪酸酯类物质的密度特性十分必要[1-2]。
目前,已获得的脂肪酸酯类物质的密度实验数据并不全面,尤其缺少高压条件下的数据[3]。因此,建立可靠的热力学模型,预测脂肪酸酯在不同状态下的密度对于工程应用具有重要的意义。Oliveira等[4]建立了一个针对C8∶0~C24∶0的脂肪酸酯的soft-SAFT状态方程,获得了方程中的参数。Daridon[5]将基团贡献法与Murnaghan方程相结合,预测脂肪酸甲酯(C10∶0~C24∶0)压力最高达200 MPa下的液相密度,预测值绝对平均偏差基本都在0.1%以内。朱山杉等[6]对Tait方程进行了改进,使之可以预测脂肪酸酯的高压液相密度。此外,体积平移的立方型状态方程因其形式简单、预测精度高等优点,一直是国内外学者研究的热点。Schedemann等[7]和 Do Carmo 等[8]结合体积平移法对传统的Peng-Robinson(PR)方程进行了修正,得到了体积平移的PR(VTPR)方程,并将其应用于脂肪酸酯类物质的密度预测,但其体积平移量均为常数,所建立的模型不能外推至高温区的密度。此外,这些模型无法预测同类脂肪酸酯的密度。
为了进一步提升VTPR方程的预测能力,本文利用25种脂肪酸甲酯(包括19种饱和脂肪酸甲酯和6种不饱和脂肪酸甲酯)的常压密度实验数据,获得了体积平移量与温度和脂肪酸甲酯碳原子数之间的关系,以此构建了新的VTPR方程,并评估了新方程预测高压条件下密度的能力。
1 脂肪酸甲酯相关信息及VTPR方程
本文所研究的25种脂肪酸甲酯的基本信息如表1所示。构建VTPR方程需要知道物质的临界温度Tc、临界压力pc、临界比体积Vc及偏心因子ω等。部分脂肪酸甲酯会在到达临界点之前发生分解反应,无法通过实验获得其临界性质[9]。因此,对于缺乏临界数据的脂肪酸甲酯,本文采用Do Carmo等的基团贡献法获得[8,10],结果如表1中带下划线的数据所示。
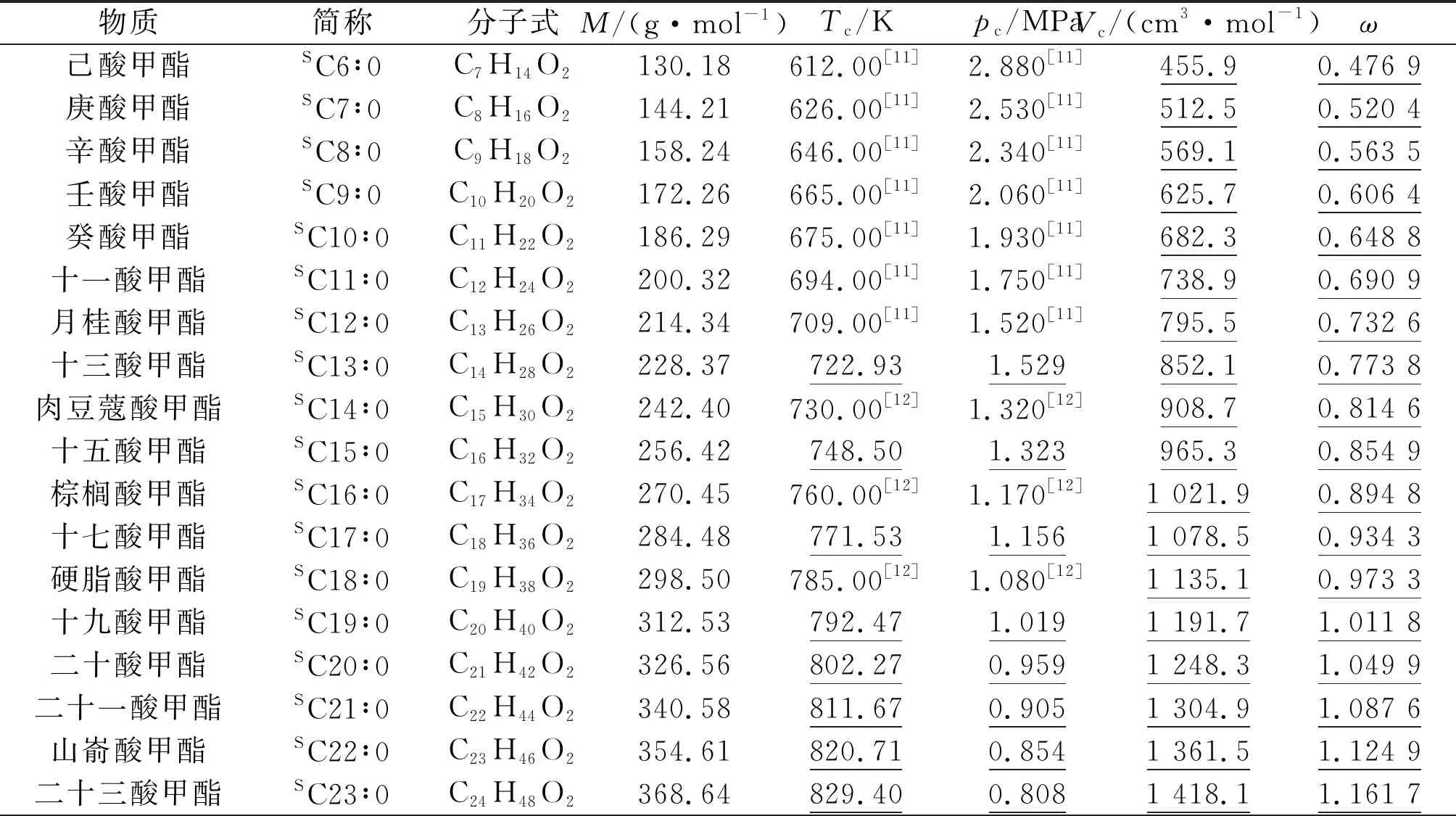
表1 脂肪酸甲酯的基本信息
脂肪酸甲酯在常压条件下的密度实验数据如表2所示,共计837个数据点。
体积平移的概念由Martin[24]在1979年提出,该方法可大大改善立方型状态方程对物质液相密度的预测能力,因此得以广泛应用。VTPR方程的表达式为
(1)
式中:c为体积平移量,可表示为由状态方程计算得到的流体摩尔体积VPR与对应的实验值Vexp的差;p为压力,Pa;R为通用气体常数,通常取8.314 J·(mol·K)-1;T为温度,K;V为摩尔体积,m3·mol-1;a和b为描述分子间相互作用和占据体积的参数,表达式为
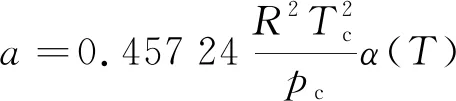
(2)
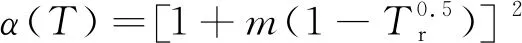
(3)
m=0.374 64+1.542 26ω-
0.269 92ω2(ω≤0.491)
(4)
m=0.379 642+1.485 03ω-0.164 423ω2+
0.016 666ω3(ω>0.491)
(5)

(6)
式中:Tr为对比温度,Tr=T/Tc。
需要说明的是,Abudour等[25]也建立了一个体积平移的VTPR方程。该模型中,体积平移量c的表达式如下
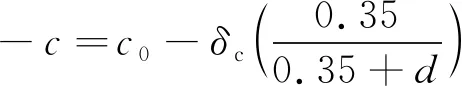
(7)
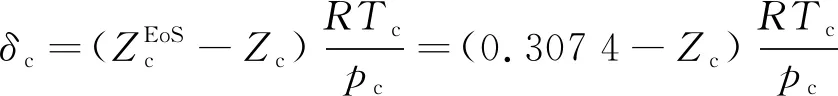
(8)
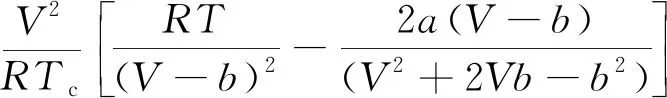
(9)
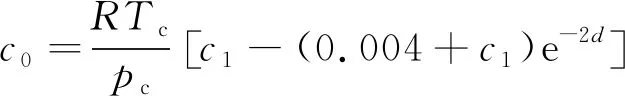
(10)
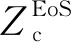
2 结果与讨论
根据式(1)~(6)以及脂肪酸甲酯的常压密度实验数据,计算得到各物质的体积平移量。图1(a)和1(b)分别给出了体积平移量csat随饱和脂肪酸甲酯中的碳原子数N和温度T的变化情况。从图1(a)可以看出,体积平移量随着饱和脂肪酸甲酯的碳原子数的增大而增加。从图1(b)可以看出,不同饱和脂肪酸甲酯的体积平移量随温度的增加呈近似线性的关系。因此,本文在构建体积平移量时综合考虑了饱和脂肪酸甲酯碳原子数和温度两个因素的影响,提出表达式
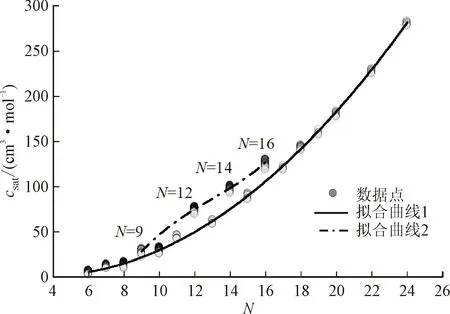
(a)体积平移量随碳原子数的变化
csat=k1+k2N+k4N2+k6N3+
(k3+k5N+k7N2)T
(11)
不饱和脂肪酸甲酯相较于饱和脂肪酸甲酯在分子结构上多一个或多个碳碳双键。本文定义不饱和脂肪酸甲酯剩余体积平移量Δc为其所需的体积平移量cunsat与对应碳原子数的饱和脂肪酸甲酯的体积平移量之差,即Δc=cunsat-csat。
在此基础上,分析了剩余体积平移量分别与碳原子数N和双键数D的关系,如图2所示。
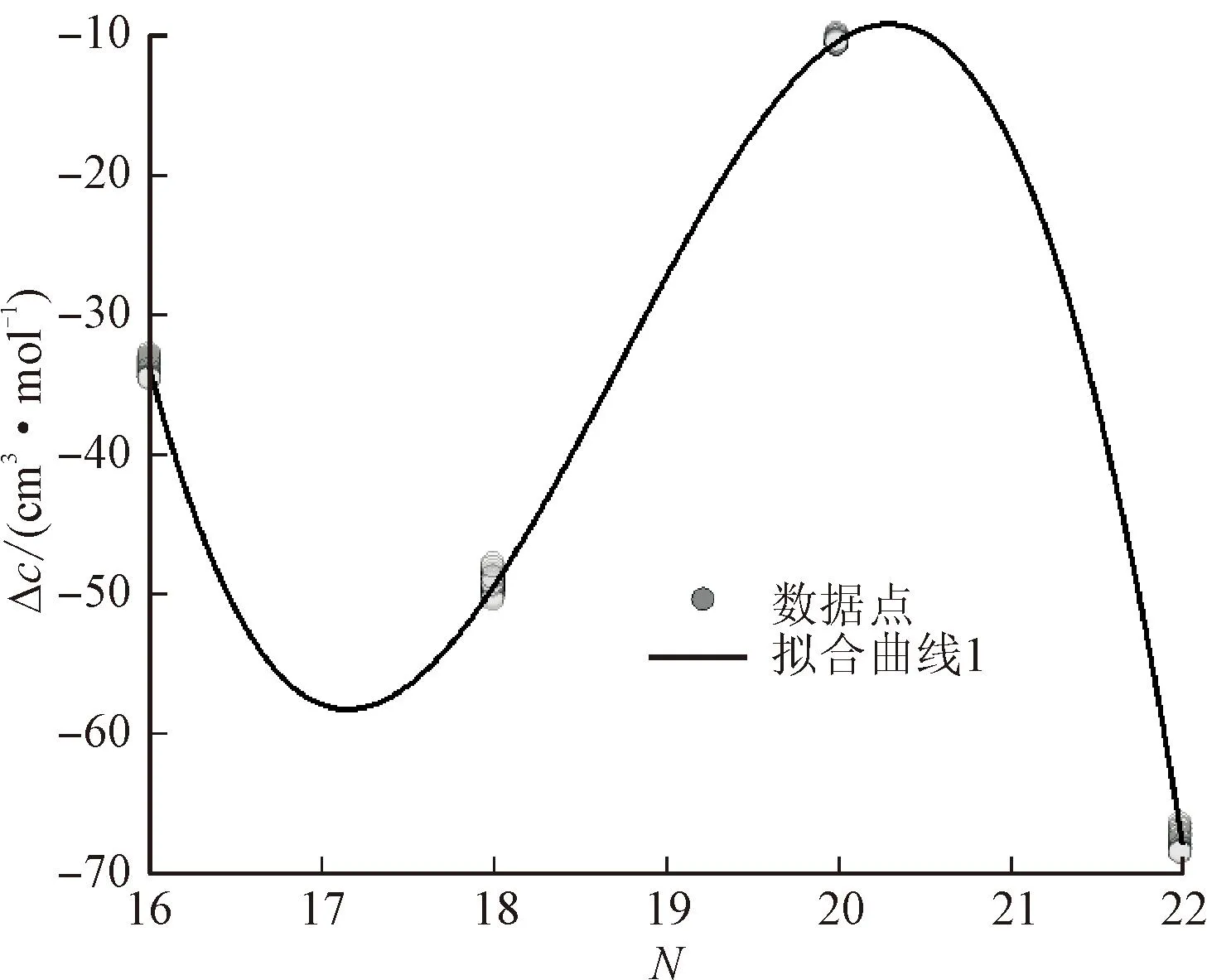
(a)D=1时剩余体积平移量随碳原子数的变化
对于不饱和脂肪酸甲酯,提出体积平移函数表达式
Δc=l1+l2N+l3N2+l4N3+l5D+l6D2
(12)
cunsat=csat+Δc
(13)
结合常压密度实验数据采用最小二乘法获得式(11)和(12)中的系数,目标函数为
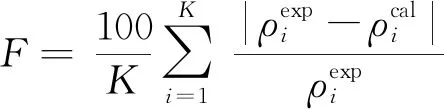
(14)
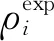
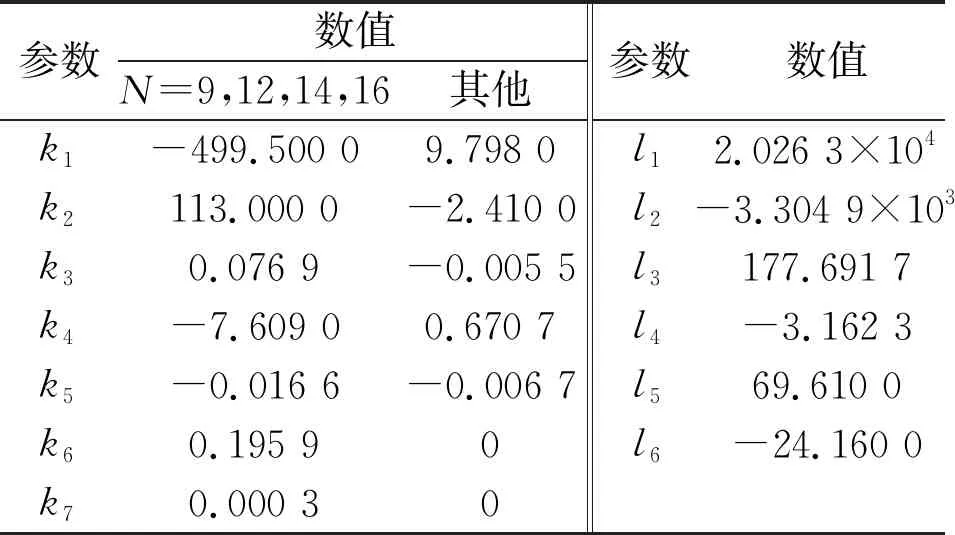
表3 式(11)和式(12)的参数回归值
为了比较本文所建立的VTPR方程的优劣,与原始PR方程、Do Carmo所建立的VTPR方程(D-VTPR方程)以及Abudour建立的VTPR方程(A-VTPR方程)进行了比较。表4给出了这4种方程密度预测值与实验值的相对偏差。总体来看,本文提出的VTPR方程对饱和以及不饱和脂肪酸甲酯的密度预测精度最高,总体相对偏差为0.30%。
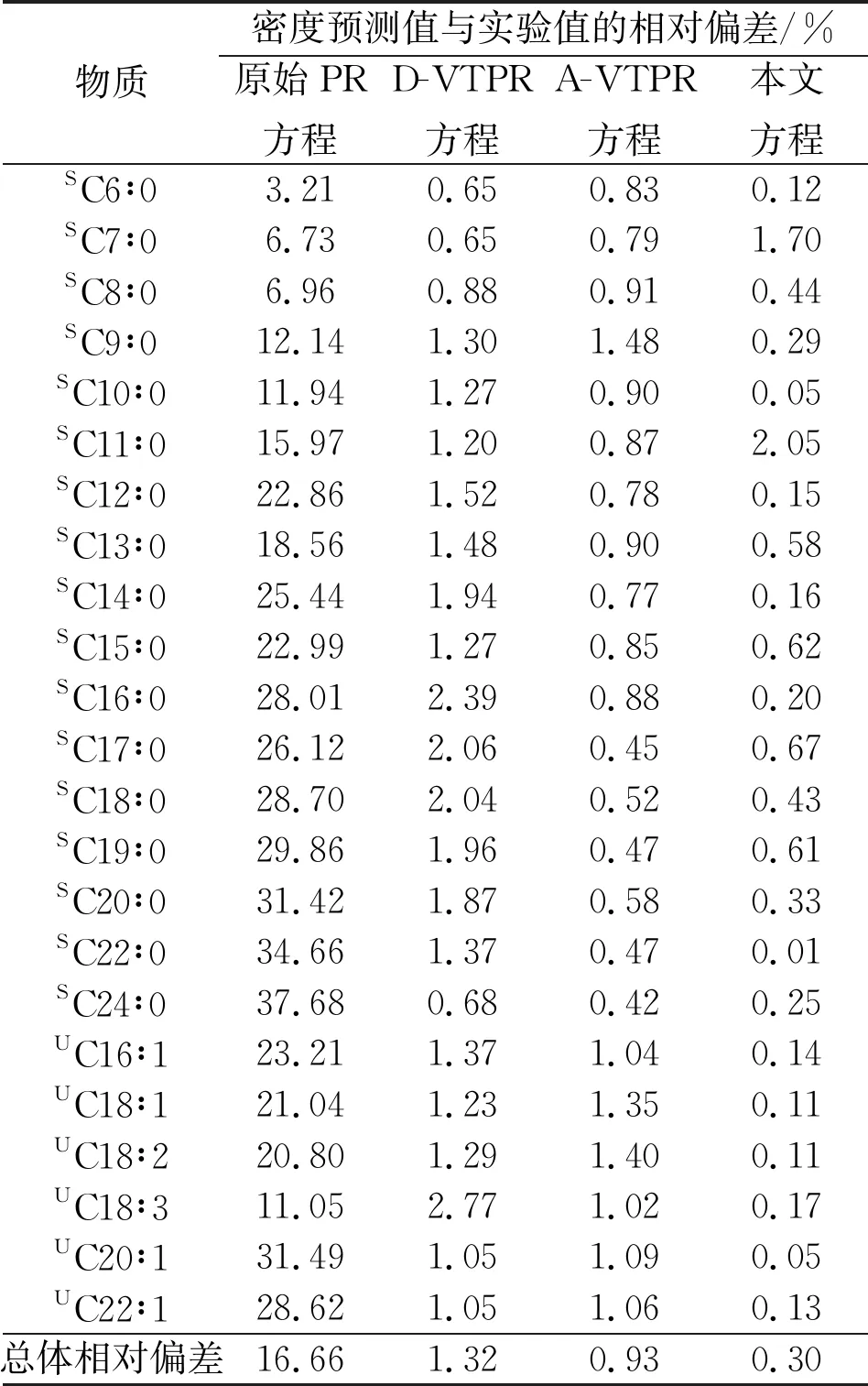
表4 不同方程密度预测值与实验值的相对偏差
本文选取了两种在生物柴油中常见的脂肪酸酯纯组分(SC16∶0和UC18∶1),给出了各方程对其在常压条件下密度预测的偏差随温度的变化,如图3和图4所示。可以看出,相较于其他几种方程,对于饱和以及不饱和脂肪酸甲酯,本文VTPR方程的密度预测偏差随温度变化的影响最小。
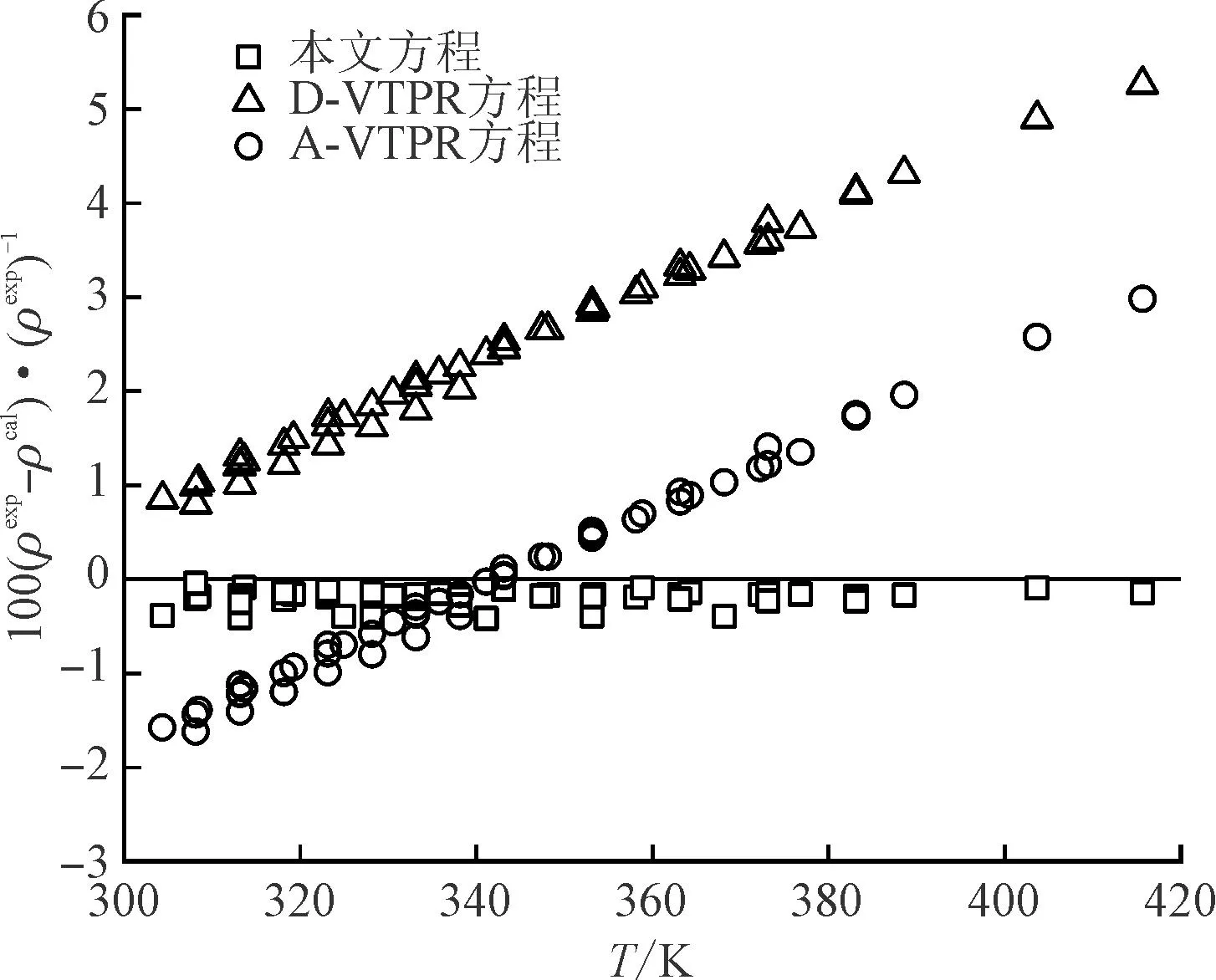
图3 不同方程对饱和脂肪酸甲酯C16∶0的密度偏差比较
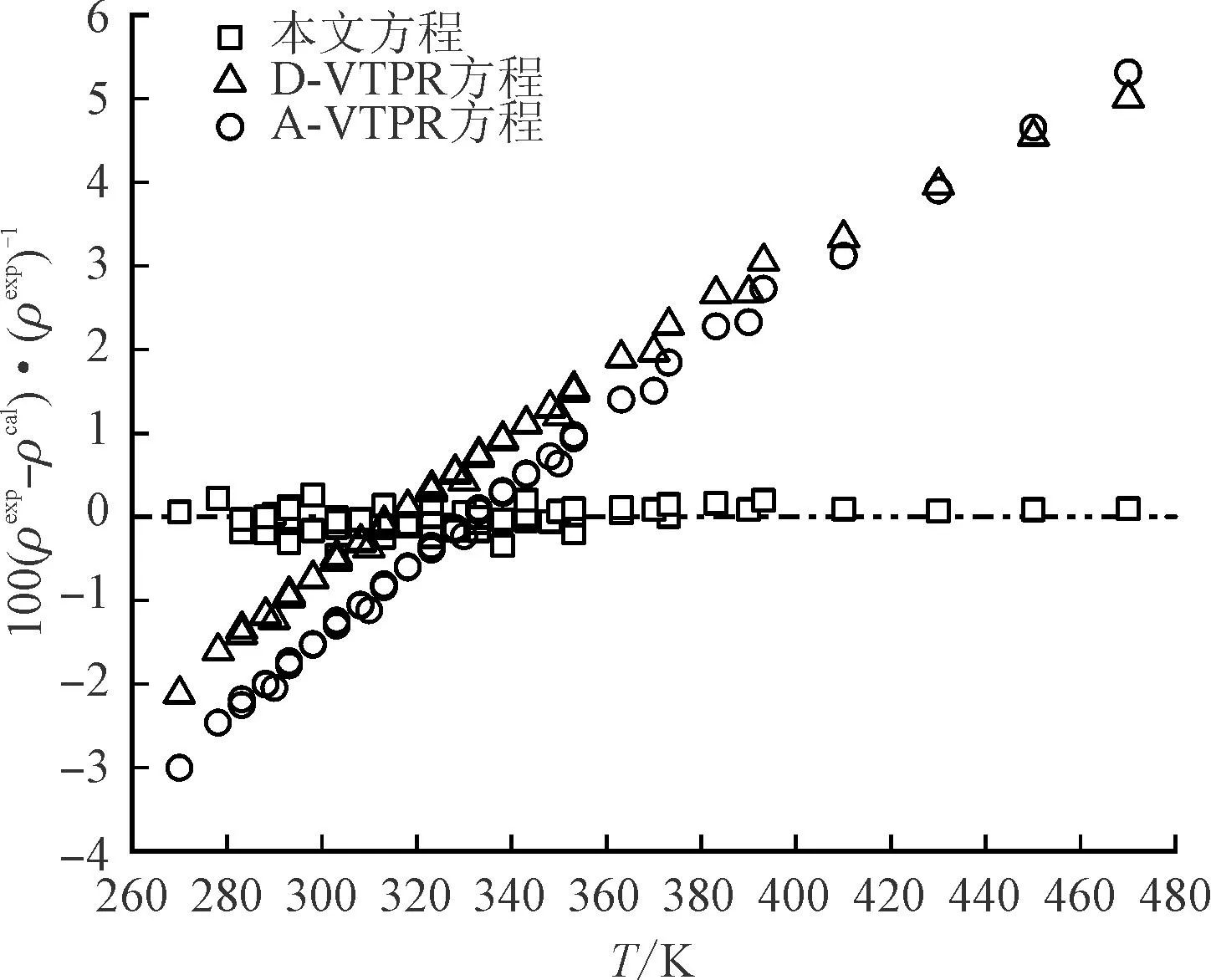
图4 不同方程对不饱和脂肪酸甲酯C18∶1的密度偏差比较
为了进一步评估模型预测脂肪酸甲酯高压密度的可靠性,收集了9种饱和脂肪酸甲酯和3种不饱和脂肪酸甲酯高压液相密度,压力最高达200 MPa,共计2 158个数据点,具体信息见表5。同时,表中给出了4种不同方程对其预测的结果。可以看出,本文的VTPR方程对12种脂肪酸甲酯高压液相密度预测结果的总体相对偏差为0.50%,优于其他方程。
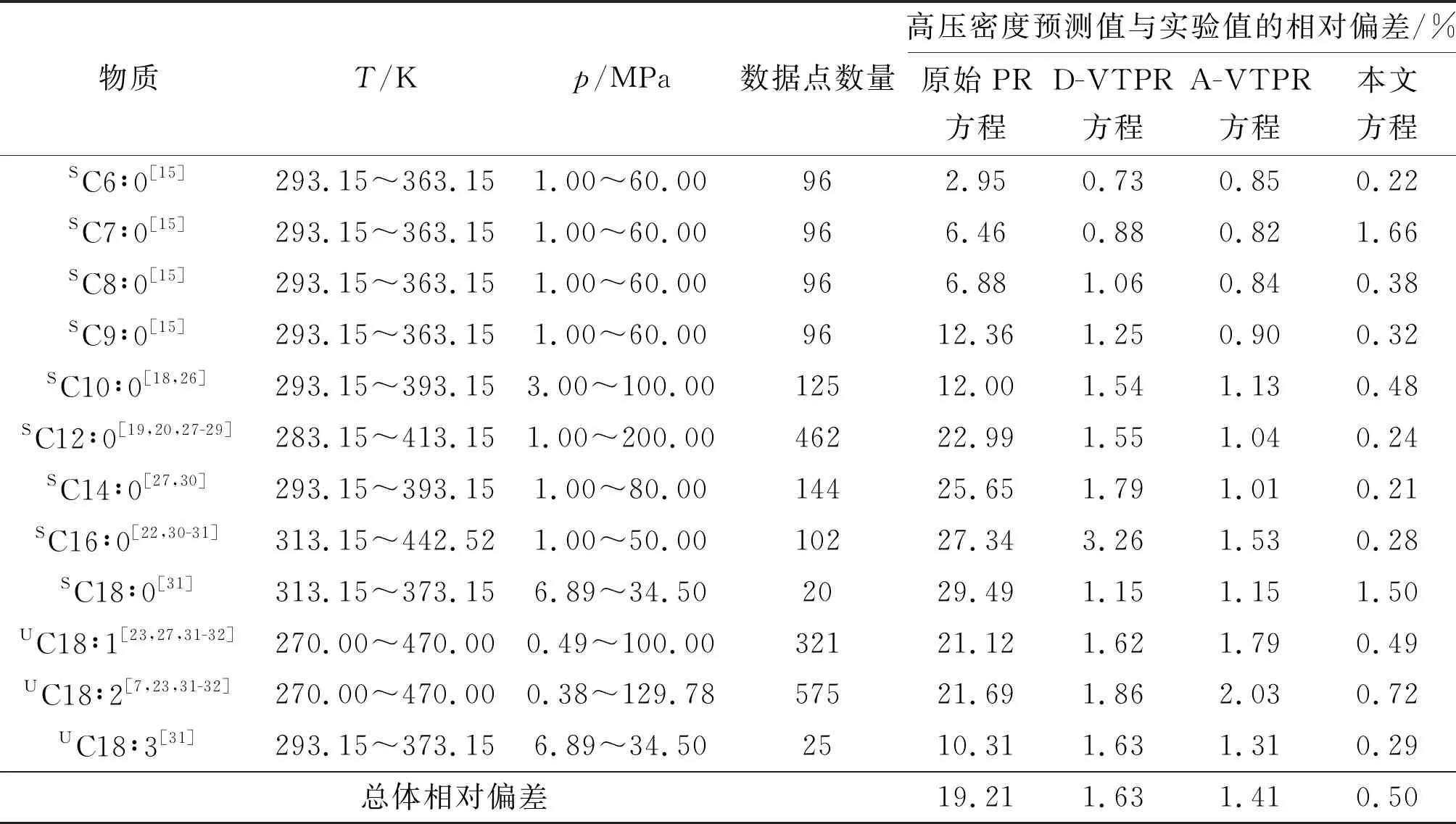
表5 高压密度实验数据收集信息及不同方程预测高压密度的相对偏差
体积平移方程有可能存在热力学不一致的问题。具体表现为在p-V图中两个低于临界温度的等温线可能会在某个压力范围内交叉。因此,2016年Shi和Li[33]提出了一个简明的标准来判断体积平移状态方程的热力学一致性。当体积平移量与温度呈线性关系,即c=AT+B,并且温度系数A为负值时,等温线在p-V图中不会出现交叉。本文得到的体积平移量对应的温度系数A仅与碳原子数N有关
A=k3+k5N+k7N2
(15)
温度系数A的计算结果如表6所示。结果表明,对于所研究的脂肪酸甲酯,方程的温度系数A均小于0,即方程在较宽的温度和压力范围内符合热力学一致性。
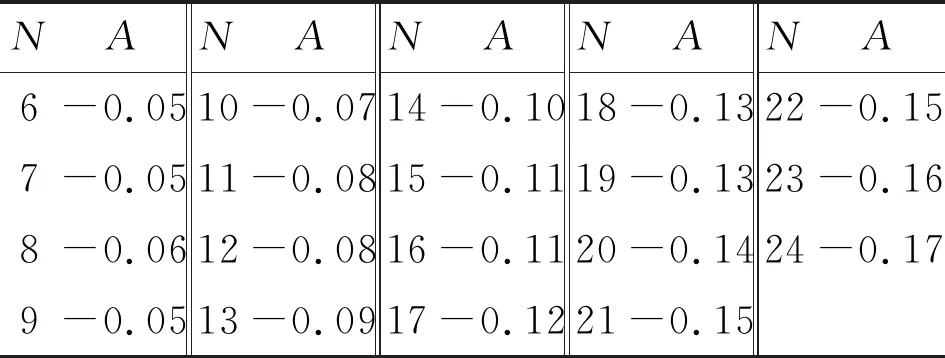
表6 不同脂肪酸甲酯的温度系数A
3 结 论
本文以脂肪酸甲酯为研究对象,采用体积平移对PR方程进行了修正,主要结论如下:
(1)采用脂肪酸甲酯常压密度实验数据,分别得到了体积平移量与饱和脂肪酸甲酯和不饱和脂肪酸甲酯中的碳原子数、双键数以及温度之间的关联式;
(2)对于得到的VTPR方程,适用对象涵盖了包括C6∶0~C24∶0在内的19种饱和脂肪酸甲酯以及C16∶1、C18∶1~C18∶3、C20∶1、C22∶1在内的6种不饱和脂肪酸甲酯;
(3)得到的VTPR方程具有预测脂肪酸甲酯高压液相密度的能力,其预测脂肪酸甲酯高压密度的总体相对偏差为0.50%;
(4) 得到的针对脂肪酸甲酯的VTPR方程符合热力学一致性。
