基于双弹光级联差频调制的波片参数测量研究

王爽，崔志英，冯华君，李克武，王志斌

（1 中北大学 计算机科学与技术学院，太原 030051）

（2 宁波永新光学股份有限公司，宁波 315040）

（3 中北大学 山西省光电信息与仪器工程技术研究中心，太原 030051）

（4 浙江大学 光电科学与工程学院，杭州 310041）

0 引言

波片是利用双折射研制的基础光学元件，通常采用具有数十微米厚度的石英晶体、MgF2晶体或聚合物制成［1］。波片能够改变光偏振状态，主要用于偏振发生装置和偏振分析装置中，在通信、传感和光存储等领域发挥着重要作用［2-4］。相位延迟和快轴方位角是波片的两个关键参数。对波片参数的精确测量和标定是波片制备中的关键步骤，直接决定了应用波片的偏振光学系统性能。

目前，国内外均开展了波片参数测量的研究工作，主要有光强法、偏振补偿法、干涉法、激光回馈法和偏振调制法等波片参数测量方法。光强法是将波片放置在正交偏振片之间，通过旋转波片，在不同角度下测量检测光强，然后计算出波片的延迟量［5］。偏振补偿法是基于Senarmont 补偿原理，在光强法基础上，在波片和检偏器之间加入一个已知延迟量的补偿器。通过旋转补偿器或检偏器，观测出射光极小时的偏振角度来实现波片延迟量测量［6］。光强法和偏振补偿法具有仪器结构简单、成本低等优势。但上述两种方法，需要机械旋转波片、补偿器或检偏器，多次测量实现波片参数测量，测量精度有限。此外，多次测量耗时，不适用于快速测量。干涉法运用迈克尔逊干涉、马赫泽德等干涉方法，将波片插入测量光路，根据测量光路和参考光路光程差计算出波片延迟量，该测量方法测量精度较高，但容易受温度、环境振动等环境因素干扰［7］。激光回馈法是将待测波片加入激光回馈腔，通过压电陶瓷驱动反射镜扫描回馈腔长，检测输出激光光强的偏振跳变来实现待测波片延迟量测量［8-9］。测量精度取决于光强稳定性，测量精度和重复性也容易受环境温度和振动干扰，而且需要对样品镀膜处理来消除杂散光干扰。

偏振调制法将电光调制、磁光调制和弹光调制等技术应用于波片参数测量。利用偏振调制实现调制交流光强信号，波片待测参量被加载在交流信号中，通过交流信号分析完成波片参数测量［10］。调制信号的分析提高了信噪比，实现了较高精度的测量。相较于法拉第旋光器、电光调制器，弹光调制技术具有高调制频率、大通光孔径、高调制纯度、工作稳定等应用优势［11］。ZENG A 等相继开发了基于弹光调制的波片测量系统，测量光路中采用单个弹光调制器（Photoelastic Modulator，PEM），通过测量弹光调制的直流、1 倍频和2 倍频信号完成波片参数测量［12］。但目前调制方法单次测量大多不能同时实现波片延迟量和快轴方位角两个参数的同时测量。

本文基于弹光调制技术优势，开展双弹光级联差频调制，及其波片延迟量和快轴方位角同时测量研究，结合数字锁相数据处理技术，实现高速、高精度的波片参数实时测量。

1 原理

波片采用具有双折射特性的石英晶体、MgF2晶体或聚合物薄膜制备而成。入射光沿两个折射率主轴方向分解为振动方向相互垂直、传播速度不同的寻常光和非寻常光［1］。两个偏振光分量通过波片后产生一个相位延迟量，表示为

式中，d为波片的厚度，no和ne分别为寻常光和非寻常光的折射率。波片通常有1/4 波片、1/2 波片等，相位延迟量分别对应90°和180°。通常将波片的寻常光折射率主轴定义为波片快轴，快轴方位角设置为θ。相位延迟量ϕ和快轴方位角θ是波片的关键物理参数。波片生产和使用时均需要严格测量和标定。利用弹光调制技术的高调制频率、大通光孔径、高调制纯度等应用优势将弹光调制技术和数字锁相数据处理技术，建立应用双弹光级联差频调制的波片参数实时测量方法。该测量方法基本原理如图1 所示。

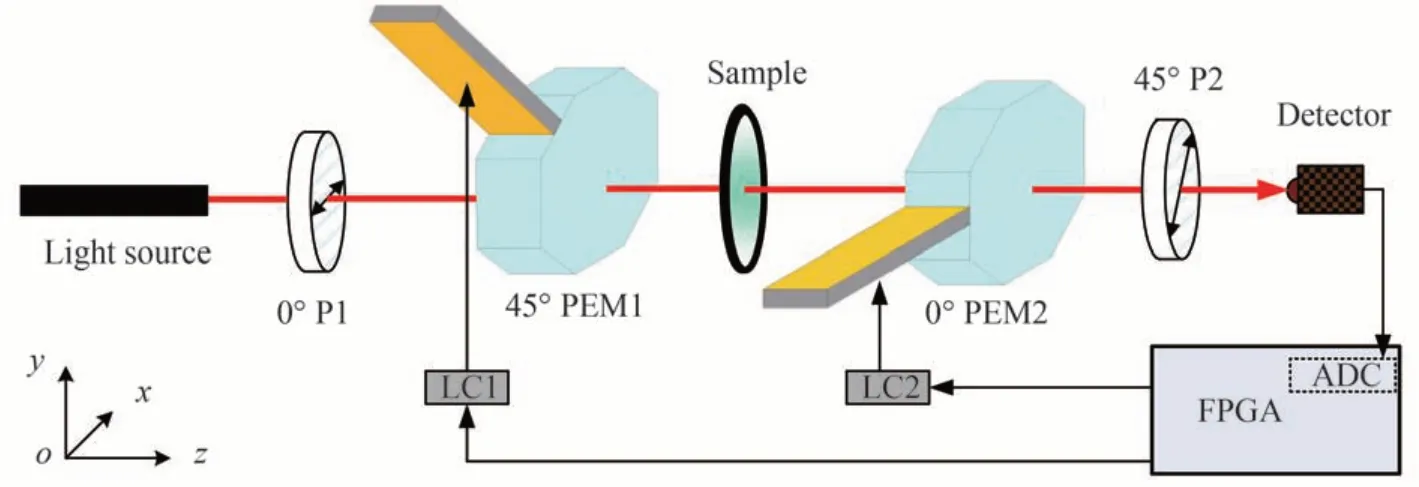
图1 波片参数测量方案原理图Fig.1 Schematic diagram of the measurement of wave plate parameter

如图1 所示，以弹光调制器1（PEM1）和弹光调制器2（PEM2）为核心构建偏振分析装置，检测光源依次经过起偏器，两个弹光调制器（Photoelastic Modulator，PEM），再经过检偏器被探测器探测。起偏器和检偏器的透光轴方向分别设置为0°和45°，两个弹光调制器的调制快轴方向分别设置为45°和0°，使整个偏振分析装置中起偏器和检偏器的透光轴方向和弹光调制快轴方向依次成45°。

为了实现波片相位延迟量和快轴方位角两个参数同时测量，本文方案选用两个谐振工作频率不相同的PEM，并且两个PEM 级联工作，构成差频调制偏振分析测量系统。待测样品设置在系统的中部。整个系统检测光信号采用Stokes 矢量描述，起偏器、检偏器、PEM 和样品的偏振传输特性采用Muller 矩阵描述［13］。检测光经过整个系统的偏振传输采用Stokes 矢量和Muller 矩阵描述为

式中，Sout表示出射光的Stokes 矢量，Sin表示经0°起偏器后的入射光Stokes 矢量，通常表示为Sin=I0[ 1 1 0 0 ]T，其中I0为入射光经起偏器透射的总光强。MPEM1和MPEM2分别表示PEM1 和PEM2 的Muller 矩阵，且PEM1 调制快轴方位角设置在45°，PEM2 的调制快轴方位角设置在0°，所以两个PEM 的Muller 矩阵可以描述为［11，13］

式中，δ1和δ2表示PEM1 和PEM2 的调制相位，且PEM 的调制相位可以进一步表示为δ1=δ10sinω1t和δ2=δ20sinω2t，其中δ10和δ20分别表示两个PEM 的相位调制幅值，ω1和ω2分别表示两个PEM 的谐振工作频率。为了同时实现波片相位延迟量和快轴方位角测量，本文方案的关键在于两个PEM 谐振工作频率不相同（ω1≠ω2），构成双弹光级联差频调制的偏振分析测量系统。

波片的偏振传输特性用Muller 矩阵描述为［6，12］

由式（4）能够看出，波片的相位延迟量和快轴方位角两个参数决定了其偏振特性。

检偏器的透光轴设置在45°方向，其Muller 矩阵表示为

将式（3）、（4）和（5）表示PEM、波片和检偏器的Muller 矩阵，连同入射光的Stokes 矢量带入式（2），并考虑探测器能够探测到的光强为Stokes 矢量的第一个分量，求解获得探测器探测到测量系统的输出光强为

式中，两个PEM 调制项sinδi=sin(δi0sinωit)和cosδi=cos(δi0sinωit)采用第一类贝塞尔函数展开得和，k=1，2，…为正整数，J0，J2k-1和J2k分别代表第0 阶，第2k-1 阶，第2k阶贝塞尔级数，PEM1 和PEM2 分别对应取i=1 和2。取k=1时考虑低阶贝塞尔级数，式（6）进一步改写为

由式（7）分析可知，波片相位延迟量和快轴方位角的相关项sin(4θ)sin2(ϕ/2)被加载在频率为2ω1、2ω2、2ω1+2ω2和2ω2-2ω1等交流项信号中，相关项cosϕ被加载在频率为ω1+ω2和ω2-ω1等交流项信号中，相关项cos(2θ)sinϕ被加载在频率为ω2、2ω1+ω2和2ω1-ω2等交流项信号中，相关项sin(2θ)sinϕ被加载在频率为ω1、2ω2+ω1和2ω2-ω1等交流项信号中。通过求解双弹光级联差频调制的不同频率成份，便能够实现波片相位延迟量和快轴方位角的同时测量。采用数字锁相技术通过FPGA 控制ADC 采样频率，将ADC 转换后的检测光强数字信号序列输入FPGA 中［14-17］，同时解调出两个PEM 的基频信号幅值Vω1和Vω2，和差频信号幅值Vω2-ω1，即

为了数据求解方便，将两个PEM 的基频信号幅值（Vω1和Vω2）和差频信号幅值Vω2-ω1求比值，定义两个通道的比值为RI和RII，即

利用式（9），同时求解出待测波片的相位延迟量ϕ与快轴方位角θ为

通过双弹光级联差频调制的偏振分析系统单次测量便能同时实现波片相位延迟量ϕ与快轴方位角θ测量。通常波片的相位延迟量参数又可采用延迟量描述为

2 实验

按照原理图1 搭建了实验系统，检测光源选用杭州新势力光电技术有限公司NewOpto-633-2-P 型氦氖激光器，波长632.8 nm，光功率2 mW，光斑直径为2 mm；起偏器和检偏器选用格兰泰勒偏振棱镜，消光比优于105∶1；PEM1 和PEM2 为作者自行研制的单驱动八角对称状结构PEM，压电驱动器为压电石英晶体，通光晶体选用熔融石英晶体。PEM1 和PEM2 的熔融石英晶体尺寸分别为60 mm×60 mm×16 mm 和54.2 mm×54.2 mm×16 mm，加工装调好的两个PEM 谐振频率分别为44.91 kHz 和49.95 kHz。探测器选用大恒光电DH-GDT-D020V 硅光电探测器，响应时间20 ns，波长范围400～1 100 nm，灵敏度为2.75 mV/μW。PEM 驱动控制及数据处理电路以Altera EPC IV FPGA 芯片为核心加工制作。两个PEM 驱动信号源采用FPGA 的DDS 模块提供驱动方波信号，经LC 谐振电路放大后驱动PEM 工作。调制光信号经光电探测器探测转换，采用12 位高精度ADC 采集输入FPGA，采用数字锁相数据处理［14-16］，同时完成基频信号幅值Vω1和Vω2，和差频信号幅值Vω2-ω1信号数据处理。

2.1 PEM 相位调制幅值设置及系统初始偏移值定标

PEM 是通过信号源经LC 谐振放大后，驱动压电晶体做长度伸缩振动，最后驱动熔融石英晶体振动。熔融石英晶体根据振动而引起的周期性双折射实现对入射光调制。对于加工制作好的PEM，其相位调制幅值与驱动电压峰峰值成正比，相位调制幅值可通过驱动电压进行精确调节。由式（7）和（8）分析可以看出，为了实现检测光调制信号中基频信号幅值Vω1和Vω2，和差频信号幅值Vω2-ω1较大，获得较好的信号数据处理信噪比，需合理设置弹光调制器相位调制幅值使第0 阶和第1 阶贝塞尔级数J0和J1取极大值。贝塞尔级数随PEM 相位调制幅值变化情况，如图2 所示。

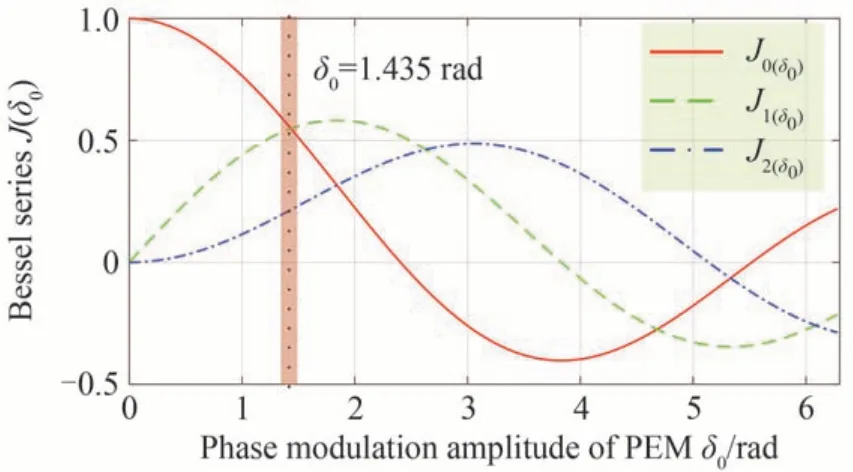
图2 贝塞尔级数Fig.2 Bessel series

依据图2 可知，将两个PEM 的相位调制幅值δ10和δ20设置在1.435 rad 附近时，式（7）和（8）中贝塞尔系数J0J1，J1J1取得极大值。本文将两个PEM1 和PEM2 的驱动电压峰峰值分别设置为190.4 V 和189.1 V时，它们相位调制幅值均达到1.435 rad。

首先，考虑到格兰泰勒偏振棱镜在实验系统中的角度误差，PEM1 和PEM2 等角度误差和剩余双折射等误差造成的测量误差，需要完成系统的初始偏移值定标。不放置任何样品时，检测激光受到两个PEM 调制，将调制光强信号进行数字锁相数据处理，获得系统初始值。数字锁相周期设置为差频信号ω2-ω1=5.04 kHz 的1 008 个周期，每间隔200 ms 测量一个数据点，记录了约1 min，300 组数据，基频信号幅值Vω1和Vω2，和差频信号幅值Vω2-ω1，如图3 所示。

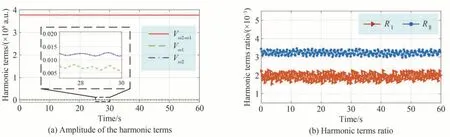
图3 调制光信号数字锁相结果Fig.3 Digital phase lock result of modulation light signals.

不放置任何样品时，测量300 次数据，数字锁相获取的差频信号幅值（ω2-ω1=3.767×108a.u.）远大于两个弹光调制的基频信号幅值（ω1=2.781×105a.u.）和（ω2=1.212×106a.u.），并且计算得出两个基频信号与差频信号的比值分别为I=1.941×10-3和II=3.220×10-3，标准偏差分别为σRI=1.19×10-4和σRII=1.86×10-4，信号比值较小。实际上，无样品时，两个比值应接近于0，但两个PEM 自身存在微小剩余双折射造成比值不为0。本文优选设计PEM 来搭建测试系统，在无样品时，基频信号与差频信号的比值较小，不超过10-3量级。此外，为了能够实现高精度的波片参数测量，本文将上述两个非零比值视为系统初始偏移值，在实际测量时，获得的信号比值都需要减去系统初始偏移值，尽可能减小，甚至消除PEM 微小双折射造成系统的测量误差。

2.2 波片参数测量实验

为了确定本文方案的测量精度和重复度，首先选用一个632.8 nm 波长的1/4 波片样品，测试过程中实验室的温度设置为23 ℃，整个实验过程实验室温度波动不超过0.1 ℃。1/4 波片为北京大恒光电的GCL-060402 型胶合石英零级波片，延迟精度为λ/300。波片安装在大恒光电GCM-1109M 型可旋转镜架中，角度旋转精度为5′。将波片放置在系统中部位置，让检测激光通过波片的中心位置，波片快轴方位角一开始旋转调节至0°方位角上。为了完成波片快轴方位角和相位延迟量两个参数的测量验证，将从0°每间隔10°旋转至180°，每个角度下记录约30 s 时长的数据。数字锁相获得的信号记录，如图4 所示。

图4（a）可以看出，差频信号幅值几乎为0，两个基频信号幅值随波片快轴方位角旋转角度变化而变化。将数字锁相获得的信号幅值连同贝塞尔级数带入式（9）求解得到基频信号和差频信号比值，如图4（b），将信号比值带入式（10）进一步求解获得波片的快轴方位角和相位延迟量两个参数，如图4（c）和（d）所示。每个快轴方位角调节的角度下测试记录约30 s 数据，约150 组测试数据点。测量结果显示，波片的快轴方位角测量值和实际值一致性较好，当角度旋转至140°±5′时，测量数据波动较大，测量获得的角度均值为=140.11°，偏差为0.11°，角度测量标准偏差为σθ=0.02°。整个过程，所有快轴方位角下波片的相位延迟量测量数据波动较小，均值为=1.572 7 rad，标准偏差为σϕ=5.57×10-4rad，表明本文测量系统具有较好的稳定性和重复性，且能够同时实现快轴方位角和相位延迟量两个参数实时测量。

为了进一步测试本文方案的波片参数测量能力，分别测试了大恒光电生产的532 nm 波长的1/4 波片和1/2 波片样品，型号分别为GCL-060401 和GCL-060411，延迟精度为λ/300。波片同样安装在大恒光电GCM-1109M 型可旋转镜架中，角度旋转精度为5′。将波片的快轴方位角调节从0°，每间隔10°步进旋转至180°，每个角度下测量记录1 次数据，总共19 个测量结果记录图5 中。

由图5 实验结果能够看出，快轴方位角测试结果与实际值吻合很好，且快轴方位角从0°旋转至180°测量过程中，波片相位延迟量测量值波动很小。图5（a）1/4 波片测试结果显示，快轴方位角从0°每间隔10°步进旋转至180°，总共19 个测量结果的相位延迟量平均值为1.313 8 rad，标准偏差为5.64×10-4rad。当快轴方位角旋转至40°±5′时，快轴方位角测量值为40.16°，和最大测量偏差为0.16°。图5（b）1/2 波片测试结果显示，相位延迟量平均值为2.597 8 rad，标准偏差为5.37×10-4rad。当快轴方位角旋转至180°±5′时，快轴方位角测量值为179.80°，存在最大角度测量偏差为0.2°。

3 分析与讨论

基于双弹光级联差频调制技术实现了波片延迟量和快轴方位角两个参数的同步实时测量。对632.8 nm的1/4 波片，532 nm 的1/4 波片和1/2 波片进行了实验测量。结果显示：波片的快轴方位角测量最大偏差为0.2°，角度测量标准偏差为σθ=0.02°；波片的相位延迟量标准偏差最大值为5.64×10-4rad，表明了本文方案及测量系统具有较好的稳定性和重复性，能够实现较高灵敏度和较高精度的波片参数测量。将本文测试结果与其他常用的波片测量方法进行对比分析，见表1。此外，本文系统数据处理基于FPGA 数字锁相技术实现，能够同时消除检测激光光强波动等测量影响，实现的单点数据测量时间仅为200 ms，适用于快速实时测量。

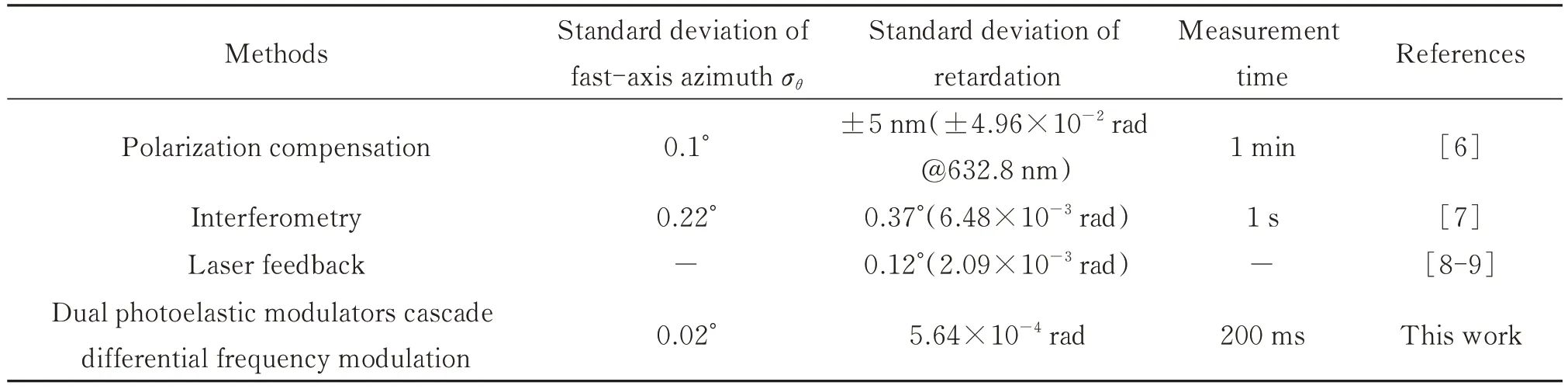
表1 波片参数测量方法比较Table 1 Comparison with reported measurement methods of waveplate parameters

然而，值得指出并探讨的是，本文方案采用氦氖激光作为检测光源，光源波长为632.8 nm，光谱带宽小于2×10-3nm，能够实现所有波片在该波长下的精确延迟量测量。但是拓展应用于其他波长时，为了保证波片参数测量的精确性，应将波片材料的双折射光谱色散加予考虑讨论。且波片的快慢轴方向不会随着入射光波长的变化而变化。根据式（11）将波片的延迟参数由相位延迟采用延迟量描述，能够看出波片延迟量是随入射波长变化而变化的。波片材料的双折射色散（ne(λ)和no(λ)）采用Sellmeier 公式可以描述为［17］

入射光波长以μm 为单位，石英波片的双折射折射率系数为：Ao=1.286 041 41，Bo=1.070 440 83，Co=1.005 859 97×10-2，Do=1.102 022 42 和Fo=100；Ae=1.288 518 04，Be=1.095 099 24，Ce=1.021 018 64×10-2，De=1.156 624 75和Fe=100。将上述系数分别带入式（12），求解获得石英波片对0.632 8 μm 和0.532 μm的入射光波长的双折射（ne-no）分别为9.272×10-3和9.144×10-3。考虑双折射色散，利用检测激光波长λ0下测量获得波片相位延迟，可以推广到针对实际应用波长λ下的延迟量参数，且描述更方便合理。结合式（11）和式（12），波片延迟量可以描述为，其中λ0和λ分别代表检测激光波长和波片实际应用波长，ϕ0为波片在检测激光波长下测量获得的相位延迟量。结合图4 和5 几个波片样品测试结果，并将双折射带入上式，计算获得波片样品的延迟量参数见表2。

表2 波片样品延迟量参数Table 2 Wave plate retardance parameter

波片测试值与理论值最大偏差为1.17 nm，满足波片出厂延迟精度为λ/300（约2.1 nm@λ=632.8 nm 波片和1.8 nm@λ=532 nm 波片）要求。本文采用氦氖激光作为检测光源，并结合波片材料双折射色散能够准确测量任何波长应用的波片快轴方位角和延迟量参数，能够为波片加工测试和实验定标提供可靠方法和手段。

4 结论

本文开展了基于双弹光级联差频调制的波片参数测量研究。两个PEM 选择工作在不同的谐振频率，以两个PEM 为核心构建偏振分析装置。波片的快轴方位角和相位延迟量两个参量被加载到弹光调制信号中。采用数字锁相技术同时提取双弹光级联差频调制的差频信号和基频信号幅值，进一步求解出波片的快轴方位角和相位延迟量。本文给出了详细的理论分析，并按照原理搭建了实验验证装置，完成了系统初始偏移值定标实验，有效地消除了PEM 自身微小剩余双折射对测量的影响；完成了632.8 nm 的1/4 波片，532 nm 的1/4 波片和1/2 波片实验测量。实验结果显示，快轴方位角测量最大偏差为0.2°，角度测量标准偏差为σθ=0.02°；波片的相位延迟量标准偏差优于5.64×10-4rad，表明本文方案及测量系统具有较好的稳定性和重复性。将波片材料的双折射色散加以考虑，根据检测激光波长下测量获得的相位延迟量，能够进一步计算出应用波长下波片延迟量值。实验测试值与理论值最大偏差不超过1.17 nm，延迟精度优于λ/300，本文实现了较高精度的波片参数测量。此外，本文实现的单点数据测量时间仅为200 ms，适用于快速实时测量。本方案实现了高速、高精度和高灵敏的波片参数测量，可为波片加工测试和实验定标提供有效手段。