面向高维小样本数据的层次子空间ReliefF 特征选择算法

程凤伟 ,王文剑 ,张珍珍

（1.太原学院计算机科学与技术系，太原，030032；2.计算智能与中文信息处理教育部重点实验室，山西大学，太原，030006）

随着互联网技术的飞速发展，信息的多样化及信息的产生速度有质的飞跃，使数据呈爆发式增长，数据挖掘［1］需要分析的对象也愈加复杂，如自然语言处理领域中的文本文档数据［2］、计算机视觉领域中的图像数据［3-4］和生物信息学领域中的基因表达数据等［5-7］，这些数据具有高维性和小样本的共性，即特征维数远远高于样本数.这类数据通常有成百上千个特征，而且，随着特征维度的急剧增加，冗余特征、噪声特征以及无关的特征都降低了分类模型的性能，因此，降维是机器学习和模式分类中的一项重要任务，特征选择是一种受到广泛关注的降维手段［8］.

ReliefF 算法［9］是一种成功的特征选择器，因简单有效而被广泛研究，其前身为Relief 算法，1992 年由Kira and Rendell［10］提出，根据各个特征和类别的相关性赋予特征不同的权重来处理两类数据的分类问题.ReliefF 算法是Relief 算法的多类扩展，可以很好地增强对噪声的容忍性.现有工作往往聚焦于对ReliefF 算法在近邻表达［11-12］、样本效率［13］、标签相关性［14-15］等方面的改进，或试图克服其在不同类型任务上面临的挑战，包括回归问题［16］、数据缺失［17-18］以及数据非平衡［19-20］等.此外，ReliefF 算法已在入侵检测［21］、医疗诊断［22-23］以及图像分类［24］等实际领域中取得了成功应用.传统的ReliefF 算法虽然可以很好地对特征进行排序，但无法去除特征冗余，即得到的特征子集中仍存在冗余项，这些冗余特征会影响分类的性能［25-27］.针对这一问题，陈平华等［28］将基于互信息特征选择的手段与ReliefF 算法结合，利用ReliefF 算法得到特征权重，再通过计算特征与特征间的互信息来剔除冗余特征.但当特征维数较高时，启发式地计算特征与特征之间的互信息的代价巨大，这类方法变得不再适用.而高维小样本数据的样本量较少，本文针对数值型的微阵列基因数据，采用邻域粗糙集理论来度量特征子集及特征的依赖度，从而剔除冗余信息，这比计算互信息的方法［26-29］更高效.

特征维数较高时，在分类任务中构造特征子集通常采用“一刀切”的方式，即截取与标记相关性较高的若干特征来进行分类，但这种方式忽略了特征组合对分类结果的影响.在特征选择中，将权重高的特征组合起来不一定有好的分类性能，因此前m个特征组成的子集不一定是分类性能最好的特征子集［30］.基于子空间的技术是一种很好的考虑全局信息的手段，刘景华等［31］提出基于局部子空间的特征选择方法，根据重要性的不同程度在子空间中设定不同的采样比例来进行选择，以提高算法的分类性能.然而，该方法基于互信息来剔除冗余特征，在特征维数较高时代价较高，且该方法按特征权重的大小排序后进行采样来选择特征，没有考虑不同的特征组合对分类性能的影响.

针对以上问题，本文提出基于层次子空间的ReliefF 特征选择算法（Hierarchical Subspace-Based ReliefF，HS-ReliefF），其主要思想是，首先，将原始特征集划分成具有两层层次结构的子空间，其中高层子空间利用随机法划分获得，低层子空间按照ReliefF 算法对特征赋权的大小排序后进行升序均匀划分获得；然后，利用邻域粗糙集理论来度量低层子空间的局部依赖度，经阈值筛选后批量地剔除冗余特征；最后，提出“局部领导力”的概念，保留部分无法直接剔除的子空间中“带队”能力较强的特征.重复多次以上过程来求取特征权重的均值，得到最终的特征权重向量，根据实际情况挑选特征子集进行后续的分类任务.

1 相关工作

1.1 ReliefFReliefF 算法［9］是Relief 算法的扩展，其通过选取k个最近邻样本点来应对不完备和噪声数据，使特征选择器更加鲁棒.ReliefF 算法从训练集中随机选择一个样本Ri，然后从和Ri同类的样本中选取k个最近邻样本NHt(t=1，…，k)，同时，从和Ri不同类的样本中寻找k个最近邻样本Mt(t=1，…，k).ReliefF 更新特征的权重如下：

其中，NMt(C)为第C个不同类的第t个最近邻点，P(C)为类C的先验概率，以上过程重复m次.

1.2 邻域粗糙集粗糙集理论中通常把特征称为属性，本文涉及的邻域粗糙集的相关内容均用属性表示特征.本节主要介绍邻域粗糙集下的正域、依赖以及属性的重要度［32］.

定义1给定实数空间上的非空有限集合U={x1，x2，…，xn}，对于U上的任意样本xi，定义δ-邻域为：

其中，dist(x，xi)为距离函数，δ≥0.

定义2给定一邻域决策系统NDS=U，A，D，决策属性D将论域U划分为N个等价类(X1，X2，…，XN)，∀B⊆A，则决策属性D关于特征子集B的上、下近似分别为：

可得决策系统的正域为：

定义3给定一邻域决策系统NDS=U，A，D，∀B⊆A，决策属性D对条件属性集B的依赖度为：

若γB-a(D)＜γB(D)，那么a对于B是必不可少的；否则，γB-a(D)=γB(D)，那么a是多余的，D对于子集B中的属性a的依赖度为0.

2 基于层次子空间的ReliefF 特征选择算法

简单地说，HS-ReliefF 算法主要包含两部分：一是结合层次子空间技术与邻域粗糙集理论来批量地剔除冗余特征；二是引入“局部领导力”考量特征对其所处子空间的相对依赖程度，保留部分较为重要的特征.

2.1 批量剔除冗余特征高维小样本数据的特点之一是特征维数较高.子空间（Subspace）技术是一种有效的特征粒化手段，将原始的高维特征空间降低为多个低维的特征空间，这样可以从局部角度处理数据，或使用契合分布式模型、集成模型等，提高计算效率与性能.刘景华等［31］提出局部子空间技术，即通过计算特征与标记集合之间的互信息来对特征进行排序，按特征权重的大小将原始特征集均匀地划分为三个子空间，根据不同的重要程度在子空间中设定不同的采样比例，进一步在每个子空间中计算特征与特征之间的互信息来剔除冗余特征.显然，此方法仅适用于特征维数较低的数据，因为在高维数据中启发式地计算特征与特征之间的互信息的代价较大，且度量单个特征的重要度的过程在大部分情况下也是多余的，因此，批量地剔除冗余特征不失为一个较好的选择.本文提出一种层次子空间的手段，将原始特征集划分成具有两层层次结构的子空间，具体操作如下.

（1）利用随机法将原始特征集划分为K个子空间，这一层为两层结构中的高层，记为H level.与刘景华等［31］按照权重大小划分子空间的方法相比，随机法考虑了不同特征组合对分类性能的影响，且本文采取多次随机划分求取平均的方式来增强模型的鲁棒性.

（2）高层中的每个子空间需要进一步进行划分.在ReliefF 算法对特征排序的基础上，按照权重大小对H level 的K个子空间依次进行均匀划分，得到K×N个子空间，这一层为两层结构中的低层，记为L level.此过程是为接下来批量剔除冗余特征做准备.

高维小样本数据的另一个特点是样本数量较少.和计算特征与特征之间互信息的方法相比，利用邻域粗糙集来构造数值型数据的特征重要度要简单得多，在划分好的子空间的基础上，依次度量低层子空间的依赖度，直接剔除依赖度小于阈值的子空间，便可以高效地批量剔除冗余特征.

定义5给定一邻域决策系统NDS=，A为原始特征集，∀B⊆A，B为其中任意一个H level 子空间，∀R⊆B，R为子空间B下的任意L level 子空间，则在高层子空间B下，决策属性D对低层子空间R的依赖度为：

定义6给定一邻域决策系统NDS=，A为原始特征集，∀B⊆A，B为其中任意一个H level 子空间，∀R⊆B，R为子空间B下的任意L level 子空间，则在高层子空间B下，低层子空间R的重要度定义为：

定义5 和定义6 给出了低层子空间的局部依赖度和局部重要度，通过设置阈值来剔除重要度较小的子空间，达到批量剔除冗余特征的目的.

2.2 考虑局部领导力的特征加权方法高层子空间使用随机法划分获得，经过多次随机划分求取平均的方式可以增强模型的鲁棒性.随机划分的另一个好处是可以对重要度不同的特征进行随机组合，结合局部与全局的角度给予特征更客观的评价.因为低层子空间中特征的重要度是一个相对的概念，对于依赖度处于阈值边缘的低层子空间，不仅要剔除其中的冗余特征，还要对保留的特征进行进一步的评价.若子空间的整体依赖度很大且其中的冗余特征较多，则被保留的重要的特征“带队”能力越强，应给予更高的权重.对此，本文提出“局部领导力”的概念，即结合特征在子空间中的表现以及其所在子空间的整体表现来共同评价该特征.

定义7给定一邻域决策系统NDS=，A为原始特征集，∀B⊆A，B为其中任意一个H level 子空间，∀R⊆B，R为子空间B下的任意L level 子空间.∀a⊆R，低层子空间R中属性a的重要度为：

则该属性a的“局部领导力”（Local Leadership，LLs）定义为：

其中，Softmax 函数为：

其中，zi表示第i个属性的重要度，C为子空间R中的属性个数.Softmax 函数能体现子空间中每个属性与其他属性的“差距悬殊”程度，这种差距的悬殊即反映了属性的“带队”能力；同时，结合当前子空间R的整体依赖度，构造属性a的“局部领导力”，在高层子空间多次随机划分的前提下，同时从局部和全局的角度为属性a额外增加更客观的评价来更新属性a的权重.更新公式为：

2.3 基于局部子空间的ReliefF 特征选择方法前文介绍了层次子空间法以及考虑局部领导力的特征加权法.层次子空间法将原始特征集划分为具有层次结构的子空间，这样可以批量地剔除冗余信息；考虑局部领导力的特征加权法构造了“局部领导力”的评价标准，在保留部分重要特征的同时，可以给予特征更客观的评价.HS-ReliefF 算法的详细步骤如下，示意图如图1 所示.由于无法确定数据集中实际存在的冗余特征个数，设定输入参数T，表示在每个高层子空间中预设的剔除子空间的数量.

图1 本文算法的示意图Fig.1 The schematic diagram of our algorithm

3 实验设计与结果

3.1 数据集及实验设置为了测试提出的算法的有效性，选取六个微阵列基因数据集进行实验，表1 为所有数据集的详细信息，所有数据均经过归一化处理.

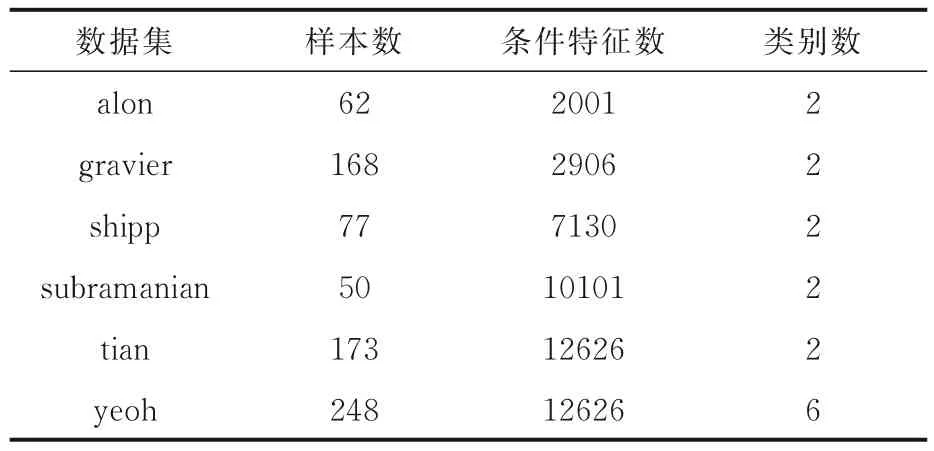
表1 实验使用的数据集描述Table 1 Description of datasets used in experiments

由于数据样本量较小，采取3 折交叉验证，用KNN 分类器对特征选择结果进行测试.对比算法为：特征选择结果采用全部特征的ReliefF 算法（ReliefF）、特征选择结果截取前I个特征（Cut I）的ReliefF 算法（ReliefF-CI）以及MFSLS 算法［31］.为公平起见，将MFSLS 算法利用计算特征与标记集合的互信息得到的初始化特征权重改为利用ReliefF 算法得到的特征权重，且该算法的采样比例直接选择最好的结果[0.6，0.3，0.1]，即MFSLS-631.所有实验在3.6 GHz Intel Core 和16 G 内存的电脑上完成，Windows 10，Matlab R2014a.

3.2 参数选择实验中的一个主要参数为最终挑选出来用于分类任务的特征子集的特征数I.由于MFSLS-631 算法在构造子空间时的特殊性，其最终挑选的特征子集的大小固定为数据集全部特征维数的1/3，对此，本文在高维的微阵列基因数据上也保持MFSLS-631 算法的参数设定.对于HS-ReliefF，ReliefF 以及ReliefF-CI 算法，设置I的大小占全部特征维数的比重的取值为[0.1，0.2，0.3，0.4，0.5]，这样设置的目的是I较小时，可以体现特征选择结果的好坏，I较大时可以体现冗余特征剔除结果的好坏.下文中I的取值直接用比重代替特征数.

本文提出的HS-ReliefF 算法中，影响冗余剔除的参数主要是预设的剔除子空间的数量T、剔除子空间时的重要度阈值θ以及低层子空间保留重要特征的阈值δ.其中，与参数I直接相关的是T和δ.根据HS-ReliefF 算法中Step 4 所述，参数T决定了需要进行筛选的特征的数量，即可能被剔除的特征的范围.T越大，说明需要筛选的特征越多，得到的结果越准确客观.最终挑选的特征子集的特征数由I决定，因此将参数T设定为：

由于HS-ReliefF 算法采用多次随机求取平均的方法，高层子空间及低层子空间的个数的设定对结果的影响不大，因此，实验中统一设定每个高层子空间包含100 个左右的特征(SB=100)，低层子空间包含10 个左右的特征(SR=10)，相应地，设置参数K=A/SB，N=SB/SR.此外，子空间保留重要特征的阈值δ直接决定低层子空间中需要被剔除的冗余特征的数量，但由于无法准确获知冗余特征的具体数量，只能人为指定阈值δ，本文设定δ∈[0.1，0.4]，并在3.3 对阈值δ进行实验分析，选取最佳结果.最后，对于剔除子空间时的重要度阈值θ，Praveena et al［22］指出θ应设置为一个非常贴近0 的正数，本文设置θ=0.01，这样可以保守地批量剔除冗余特征，尽可能避免误删有用的特征.

3.3 实验结果及分析为了保证实验对比的公平性，分别在挑选的特征子集维数相同和不同的情况下进行对比，实验结果如表2 和表3 所示，表中黑体字表示在各数据集上最好的结果.

表2 特征子集维数相同时各算法平均精度对比(I=0.33)Table 2 The average accuracy of each algorithm with the same dimension of feature subset (I=0.33)

表3 特征子集维数不同时各算法平均最大精度的对比(I∈[0.1,0.2,0.3,0.4,0.5])Table 3 The average maximum accuracy of each algorithm with different dimension of feature subset (I∈[0.1，0.2，0.3，0.4，0.5])

表2 展示了在特征子集维数相同的情况下各算法用于分类任务的平均最大精度，其中特征子集的大小固定为数据集全部特征维数的1/3，即I=0.33.由表可知，在统一特征维数的情况下，本文的HS-ReliefF 算法能更有效地剔除冗余特征，提升分类性能；MFSLS-631 算法在这些高维数据上表现欠佳，因为该算法在采样时舍弃了部分特征，这些特征在高维数据中可能同样是重要的，也正因如此，其性能表现不如“一刀切”的方法（ReliefF-CI）.

鉴于此，单独分析ReliefF-CI 和HS-ReliefF算法在特征子集维数不同时表现出的性能差异，验证本文提出的方法在考虑特征组合方面的有效性，实验结果如表3 所示.表3 展示了在特征子集维数不同时ReliefF-CI 和HS-ReliefF 算法用于分类任务的平均最大精度对比，其中，ReliefF 算法为基准算法，ReliefF-CI 和HS-ReliefF 算法在截取特征子集时保持相同的特征数.由表可知，本文的HS-ReliefF 算法在大多数情况下都有最优或相当的性能.值得注意的是，当I=0.1，0.2 和0.3 时，ReliefF-CI 和HS-ReliefF 算法在subramanian，tian 和yeoh 数据集上表现的性能相当，而且都显著优于基准算法.这是因为上述三个数据集的特征维数都较高，I较小时选择的特征质量相当，几乎不受冗余特征的影响，因此，在增大I以后（I=0.4 和0.5 时），HS-ReliefF 算法在剔除冗余特征方面的优势得到了部分体现.

此外，由于子空间保留重要特征的阈值δ决定了被剔除的冗余特征的数量，进而影响不同特征子集维数下的分类性能，本文在三个代表数据集alon，subramanian 和tian 上分析了HS-ReliefF算法在选择不同的δ时对分类性能的影响，实验结果如图2 所示，图中不同的I对应的最高柱点与表3 的结果互相对照，颜色越浅，性能越好.由图可见，当I很小（I=0.1，0.2 和0.3）时，该算法在三个数据集上的分类性能几乎不受δ的影响，这是由于此时包含冗余特征的概率很小.I增大（I=0.4 和0.5）时，阈值δ的选择会影响挑选特征子集的分类性能.在alon 数据集上，整体性能随着I的增大呈下降趋势，因此，δ较小时，算法可以保留有价值的特征，表现更好；在subramanian 和tian数据集上，算法的整体性能却呈上升趋势，因为δ较大时，算法更能剔除所选特征子集中的冗余特征，表现更好.

图2 在不同维数的特征子集上HS-ReliefF 算法阈值δ 的选择对其分类性能的影响Fig.2 Classification performance of HS-ReliefF with different threshold δ on different dimensional feature subsets

额外地，图3 展示了各算法在六个数据集上的分类性能受特征子集维数的影响情况，其中，ReliefF 和MFSLS-631 算法始终保持固定的特征子集维数，在图中用实心点和实心块表示.根据分析，不同的数据集中包含的冗余特征数不同，当特征子集维数较小时，分类性能受到特征对于标记的分类信息影响，当特征子集维数较大时，分类性能受到特征子集中冗余特征的数量影响.由图可知，本文提出的算法无论在特征子集维数较小或较大时，都有不错的表现.

图3 不同维数的特征子集下各算法分类性能对比Fig.3 Accuracy of each algorithm on different dimension feature subsets

最后，对比MFSLS-631 和HS-ReliefF 算法处理数据的时间消耗，实验结果如表4 所示，表中黑体字表示耗时较少.由表可见，高维数据中，计算特征与特征之间互信息的代价十分大.对于给定的邻域决策系统，其时间复杂度为O(|U|·|A|2)，而利用邻域粗糙集理论处理数据的复杂度为O(|A|·|U|2)，由于高维小样本数据的样本数普遍很小，即|U|≪|A|，因此，本文提出的HS-ReliefF 算法在处理数据的时间消耗方面有很大优势.此外，HS-ReliefF 算法始终在RliefF 算法得到的初始特征权重向量上进行权重调整，没有增加额外的空间复杂度.

表4 各数据集上MFSLS-631 和HS-ReliefF 算法处理数据过程的平均时间(单位：s)对比Table 4 Average dealing time (unit：s) of MFSLS-631 and HS-ReliefF on each dataset

4 结论

现有的改进ReliefF 算法在高维小样本数据上通过计算特征与特征之间的互信息剔除冗余特征，代价较高，而且没有考虑特征之间的组合对分类性能的影响.因此，本文提出基于层次子空间的ReliefF 特征选择算法HS-ReliefF，将原始特征集划分为具有层次结构的子空间，利用邻域粗糙集理论批量地剔除冗余特征，大大提高了算法的运行效率；同时，引入“局部领导力”的概念，考虑不同特征组合对算法性能的影响，从局部和全局的角度共同给予特征更客观的评价.

在六个微阵列基因数据集上的实验表明，与现有算法相比，HS-ReliefF 更高效，且能保持良好的分类性能.值得说明的是，HS-ReliefF 算法同时也是一种处理高维小样本数据的框架，可以很好地契合分布式、集成式等系统，更高效地完成任务.

算法的不足之处在于控制剔除冗余特征的阈值仍须人为指定，不能确定最佳特征子集.如何自适应地确定相关参数是下一步研究的重点.