深度混合型邻域搜索模型求解CVRP 问题

杨笑笑,陈智斌

（昆明理工大学理学院，昆明，650000）

车辆路径问题（Vehicle Routing Problem，VRP）是组合最优化问题中的经典问题，带容量的车辆路径问题（Capacitated Vehicle Routing Problem，CVRP）是VRP 的主要变体之一，在智能交通、物流领域等有广泛应用［1］.CVRP 考虑的是带容量的车队为一系列客户提供服务的最佳路线，要求车队将货物从仓库运输到指定客户点，每个客户只允许被访问一次，其中车辆是同质的且只能从仓库出发，完成任务后需返回仓库，目标是使车队完成所有任务的总路线最短［2］.先前求解组合最优化问题的方法主要依赖传统算法［3］，例如利用精确算法、近似算法或启发式算法进行求解.针对CVRP 问题的特点，国内外学者设计了各种优化算法对其进行求解，其中应用较多的是智能算法，如遗传算法、邻域搜索等.

高效的算法可以快速合理地规划路线，减少路径花费.在实际应用中具有挑战性的问题大多数是NP 难的，传统算法在处理这类任务时会受到特定的限制（例如计算时间长、精度低等）.强化学习（Reinforcement Learning，RL）在处理自然语言处理问题上的最新进展［4］表明其在处理NP难问题上具有很大的潜力.Kool et al［5］基于注意力机制（Attention Mechanism，AM）提出的Transformer 模型是首次解决旅行商问题（Travelling Salesman Problem，TSP）、CVRP 和其他路径问题的模型，模型将输入元素分为静态、动态两种类型，利用嵌入的编码过程对静态和动态元素进行向量表示，解码阶段将静态元素向量输入解码中获得隐含层向量并与动态向量结合，通过AM 获得下一个决策点的概率分布.AM 模型的提出为后续深度强化学习（Deep Reinforcement Learning，DRL）求解路径问题奠定了基础，为组合最优化问题的求解提供了新思路［6］.DRL 得到的策略有希望比人工设计的更高效，对于类似的问题能同样用基于学习的框架去求解，不需要人工重新设计算法.

基于DRL 的方法通过归一化的AM 获取隐藏层信息，但是AM 模块的性能受到CVRP 中动态和随机因素的影响，导致先前工作中的AM 模块未能充分考虑多重头注意力机制（Multi-attention Mechanism，MHA）中查询向量Q和键向量K之间的相关性，导致在没有相关性的前提下也会输出关联值.同时，混合模型通常利用多个网络进行编码和解码，结合了来自不同模块的优点，但是向量编码及传输过程过于繁杂，可能出现信息解码错误等情况.

自适应大邻域搜索（Adaptive Large Neighborhood Search，ALNS）是受大邻域搜索（Large Neighborhood Search，LNS）发展启发而来的，在LNS 的基础上，允许在同一个搜索中使用多个破坏算子和修复算子来获得当前解的邻域，根据生成的解的质量，选择表现好的破坏算子和修复算子，再次生成邻域进行搜索.邻域搜索算法的关键是邻域结构的选择，但每次迭代搜索的时间较长，缺少在解空间内自主搜索的能力.

现实中很多问题本质上是组合优化问题，因此，人们一直在修改ALNS 来有效地求解组合优化问题，例如CVRP 问题.针对上述问题，本文提出深度混合型邻域搜索（Deep Hybrid Neighborhood Search，DHNS）算法模型，即带有DRL 的ALNS 算法的修复解的更新，同时，将AOA（Attention on Attention）［7］加入编码和解码过程.在编码过程中，AOA 可以提取节点的特征，并对节点间的关系进行建模；在解码过程中，AOA 负责筛选有价值的信息，过滤不相关或误导性信息，进一步确定注意力结果和查询之间的相关性.实验结果表明AOA 模块对于改善模型性能是有效的，优于之前基于DRL 的所有模型.

本文的主要创新如下.

（1）为了提取丰富的节点特征向量，在传统编码结构上，提出一种Transformer［8］和指针网络（Pointer Network，PN）［9］混合编码结构，并在AM上改进同时具有MHA 和AOA 的编码和解码结构.MHA 主要用于信息提取，AOA 负责提高解码器的准确性.

（2）设计了一个依赖于DRL 框架的ALNS，以探索解空间中邻域的关系，修复解决方案的任务留给通过DRL 训练的新型网络模型.将DRL集成到ALNS 中可以提高算法在解空间中的搜索范围，并提供启发式信息的指导.

1 相关工作

近年来，DRL 成为一种解决路径问题的新方法，目前基于DRL 求解VRP 的框架主要是编码和解码结构，由Nazari et al［10］首次提出，强调路径问题与DRL 的结合，这种编码-解码体系训练的模型效果与传统算法相比有很大的优势.在求解VRP 的模型框架中，首先将问题转化为图，通过网络模型编码为带有节点信息的特征向量，然后通过解码器将其解码为城市输出序列.由于编码器-解码器的通用架构是循环神经网络（Recurrent Neural Network，RNN），但是RNN 存在长距离依赖问题，会导致梯度消失和梯度爆炸.为了避免上述问题，Bresson and Laurent［11］提出一种基于Transformer模型的求解方法，在编码-解码中添加AM，为每个查询输出一个加权平均值，使模型能够关注更多有用的信息，有效缓解了梯度爆炸，降低计算成本.在此基础上，王扬和陈智斌［12］提出动态图Transformer（Dynamic Graph Transformer Model，DGTM）模型求解CVRP，并使用REINFORCE 算法提高模型的训练效率，实验结果表明模型整体性能优于专业求解器，提高了CVRP 问题求解速度，且具有较好的泛化性能.

为提高模型搜索效率，Kwon et al［13］提出一种具有多重策略优化（Policy Optimization with Multiple Optimal，POMO）的网络框架，使用DRL 来训练MHA 的多个初始节点嵌入，POMO 的低方差基线使RL 模型训练快速且稳定，且对局部最小值的抵抗力最高.实验结果表明模型性能显著提高，同时模型推理时间减少一个数量级以上.为提升智能体的选择效率，Wu et al［14］通过DRL框架改进启发式算法来求解CVRP，其中策略网络用于指导下一个解决方案的选择，并利用行动者-评论家（Actor-critic，AC）算法训练策略网络，然后通过启发式算法来提高解的质量，该模型学习到的策略明显优于传统的手工规则.

启发式算法通常需要改进其在解空间内的搜索能力，因此王原等［15］利用深度智慧型蚁群优化算法（Deep Intelligent Ant Colony Optimization，DIACO）求解TSP，DRL 结合蚁群算法提高了DRL 在解空间内的搜索能力以及蚁群算法的计算能力.此外，Ma et al［16］提出双方面协作Transformer（Dual-Aspect Collaborative Transformer，DACT）模型来解决具有动态和周期性变化的CVRP，使用双向编码器分别学习节点和位置特征的嵌入，同时使用课程学习训练模型，提高模型的采样速率.实验结果表明，DACT 优于传统的启发式算法，且具有更优的泛化性能.

为了缩小基于DRL 的方法与最先进优化方法之间的性能差距，Hottung and Tierney［17］提出了一种新颖的神经邻域搜索（Neural Large Neighborhood Search，NLNS）框架，该框架集成启发式算法以生成新的解决方案，学习机制基于具有AM 的神经网络，并设计结合到大型邻域搜索设置中.实验结果表明，该模型明显优于仅使用手工启发式算法和著名的启发式算法，并接近于最先进的优化方法的性能.但上述方法仅考虑小规模CVRP，当问题规模变大时，优化效果不理想.

2 模型介绍

2.1 CVRP 问题定义CVRP 考虑带容量的车队为一系列客户N={1，2，…，n}提供服务的最佳路线，每个客户节点i的需求为qi，要求车队v={1，2，3，…，K}将货物从仓库{0}运输到指定客户点，每个客户只允许被访问一次，客户i与客户j之间的距离为dij.其中车辆是同质的（容量为C）且只能从仓库出发，完成任务后需返回仓库，目标是使车队完成所有任务的总路线最短［2］.如果车辆K直接从客户i到达客户j，则令决策变量xijk=1，否则为0.若客户节点i的需求由车辆k满足，则yik=1，否则为0.因此，CVRP 问题可建模如下.

目标函数（1）表示最小化车辆总行驶距离，约束（2）表示每个客户节点仅能被一辆车访问一次，约束（3）用来保证运输路线上的客户总需求不能超过车辆自身承载容量，约束（4）表示若客户i，j均由车辆k配送，则车辆k必须由某点i到达j，或者车辆访问完客户i后立即访问节点j，约束（5）表示访问某点的车辆数等于离开该点的车辆数.

2.2 模型总框架DHNS 模型基于PN 和Transformer 混合编码，PN 表示和提取各种浅层的节点特征，减少参数的冗余，在此基础上利用Transformer 中MHA 机制从不同维度提取节点特征信息，最后结合动态位置编码（Dynamic Positional Encoding，DPE）［12］表示隐层嵌入的绝对位置信息.而混合编码过程程序复杂，很可能出现解码失误的情况.

因此，本文通过MHA 提取节点特征信息，AOA 通过计算MHA 中的查询向量和查询结果之间的相关性，提高解码器的精确性，结合DPE进一步提取节点间的相关性，提高模型在不同规模问题上的泛化能力.DHNS 模型的总体架构和求解思路如图1 所示，ALNS 的主要思想是通过多组破坏算子OD和修复算子OR在解空间搜索并改善当前解，对性能较好的算子给予更高的权重.对于给定的初始解，由ALNS 的破坏算子OD对初始解进行破坏，然后DRL 自动学习修复解的策略，最后模型在修复解空间中探索最优的解.

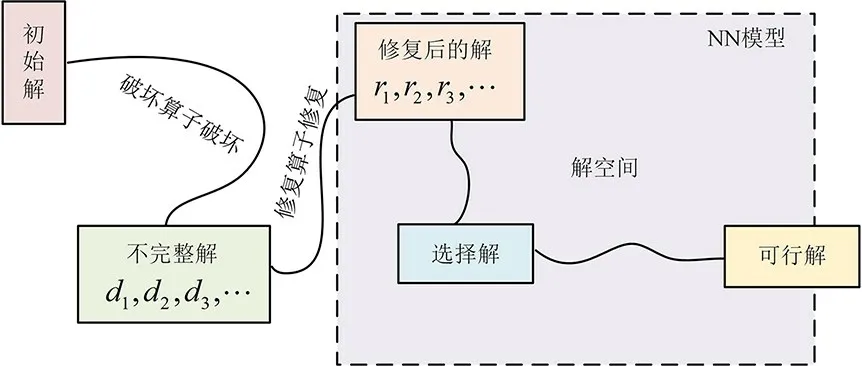
图1 模型架构及求解思路Fig.1 Model architecture and solution ideas

2.2.1 破坏算子和修复算子破坏算子OD主要通过随机破坏、点的破坏、路线的破坏对初始解进行破坏，其中随机破坏是随机破坏当前解的节点或边，基于点的破坏是删除最接近随机选择的节点，基于路线的破坏是删除最接近随机选择的节点的路线.如果一个节点vj从一条路{vi，…，vj，…，vk}移除，得到三条不完整的路.部分解{vi，…，vj-1}包含vj之前的所有节点，部分解{vj}只包含节点vj，部分解{vj+1，…，vk}包含vj之后的所有节点.图2 仅显示在邻域中破坏和修复一个解决方案的过程，但是在整个邻域中还有许多其他可能的修复解决方案.

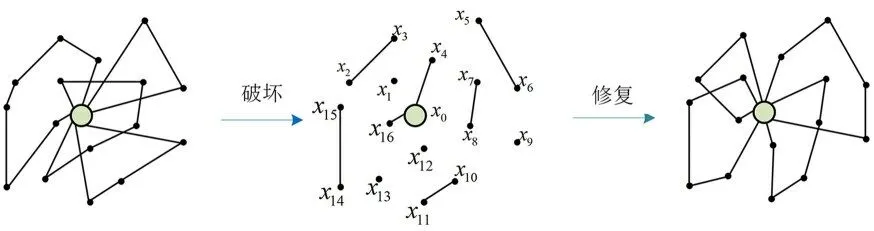
图2 破坏算子和修复算子的操作过程Fig.2 Operation process of destroying operator and repairing operator

修复算子OR主要通过DRL 在智能体与环境之间的交互作用中学习修复的策略，如图2 所示.破坏算子OD通过随机的破坏方法将初始解破坏为七段不完整路径{(x2，x3)，(x0，x4)，(x0，x16)，(x5，x6)，(x7，x8)，(x10，x11)，(x14，x15)}和四个独立的客户节点{x1，x9，x12，x13}.模型为被破坏的解的末端添加特征向量xi，并将不完整路径的末端特征向量作为输入，通过DRL 模型计算不完整路径末端节点的相关性，自动学习路径的修复策略.为了防止不完整的路径选择其末端节点或产生不可行的解决方案（例如路线负载超过车辆容量限制），通过添加掩码来禁止该操作.

2.3 编码器结构模型采用PN 和Transformer混合编码，结合两者的优势增强数据特征.如图3所示，DHNS 模型的编码器由PN，MHA，AOA，前馈层和归一化组成.首先，编码器将输入序列映射为高维向量，然后利用DPE 提取节点的特征向量a=[a1，a2，…，an]，ai∈Rd，n为客户数目，d为特征向量的维数.MHA 进一步促进网络提取深层次的特征信息，AOA 则是减少在解码阶段进行错误解码的可能性.因此，特征向量不再是直接传到解码器，而是通过AOA 和MHA 来更加精确地表示节点特征向量ai.编码部分可表示为：

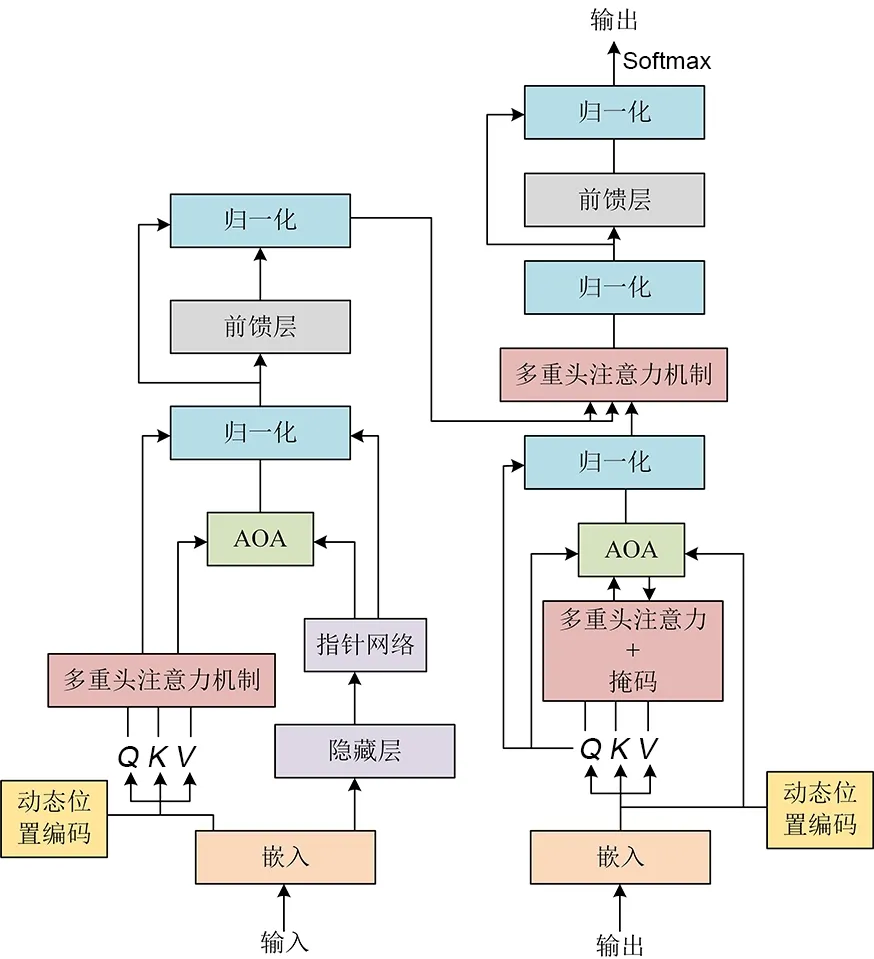
图3 DHNS 模型总架构Fig.3 DHNS model master architecture

其中，Wo是训练参数，Ql，Kl和Vl分别是自注意力机制的查询向量、键向量和值向量.

当反向传播梯度累积时，模型需要随时了解动态元素的信息变化，因此使用AM 和cos-AM［18］提供双隐层信息，分别表征动态信息和静态信息.用元组(Xt，ft)表示不完整解在t时刻的状态，对于输入xt∈Xt，包含上述过程在时间步长t时产生的嵌入hi和hi'，hi和hi'通过Embc和注意层转换计算得到，ft表示相关嵌入，Embf使用与Embc相同的结构不同的参数，通过Embf和注意层生成嵌入hf和hf'.所有节点信息嵌入都被注意层AM 和cos-AM 用来计算上下文向量c来表示所有相关嵌入.上下文向量c计算如下：

AOA 主要生成两个信息，即信息向量I和注意力门G，然后对AOA 使用逐元素乘法将注意力门G应用到信息向量I来添加另一个注意力机制，AOA 可以应用于各种注意力机制.对于传统的单头注意力机制，AOA 有助于确定注意结果与查询之间的相关性.对于MHA，AOA 有助于在不同注意力头之间建立关系，过滤所有注意力结果并仅保留有用的注意力.对于编码器，AOA 机制将自我注意应用于向量以对节点之间的关系进行建模，进而确定不同向量之间的关系.对于解码器，应用AOA 过滤掉不相关或误导性的注意结果，并仅保留有用的结果.

2.3.1 MHAMHA 首先计算了Q，K的注意分布，并将其附加到V上，此步骤准确地捕获输入序列的特征信息.然后计算Q和V的相似度并归一化，根据相似度和相应的V值加权和获得最终的注意值，此步骤通过在全局特征中分配不同的权重给不同的特征向量以提取局部特征，同时生成包括全局和局部特征在内的联合特征向量序列.根据Huang et al［7］研究使用缩放点积方法计算MHA 中的权重可以有效地解决梯度消失问题，因此使用如下表达式来计算权重向量：

其中，qi属于Q的第i个查询向量，kj和vj分别属于K，V的第j个键向量和值向量，fsim是用来计算kj和qi相似分数的函数，Hi表示qi和kj的相似性.

2.3.2 AOA模型对AM 有着全局依赖性，因为输出的结果取决于AM 的权重分配，但解码器对注意力分配的合理性或者与查询向量的相关程度一无所知.先前模型的AM 通过对每个时间步生成的特征向量做加权平均值来指导解码过程.传统的AM 不管Q，K或V是否相关，都会为Q生成一组归一化的权重，通过给出与任务相关的查询向量q的过程，通过缩放点积方法计算Q，K的注意分布，并将其附加到值向量V上，从而得到注意值.若二者不相关，会输出误导或错误的信息.最后的注意力结果可能不是解码器期望得到的，而是注意力分配造成的，将导致解码器被误导输出错误的结果.

为了避免上述误导性信息，使用AOA 模块衡量注意力结果和查询之间的相关性，来解决这种不合理的现象.AOA 通过MHA 中的Q，K和V获得的权重结果执行两个独立的线性变换来生成信息向量I和注意力门G，同时利用逐元素乘法聚合信息向量I和注意力门G以预防不合理的现象，从而提高解码器的准确性.MHA 寻找节点间的潜在联系，AOA 测量它们之间的关联程度，更新特征向量.AOA 首先使用得到的注意结果和当前上下文向量c生成信息向量I和注意力门G，信息向量I是当前上下文向量和注意力结果v通过线性变换得到并存储，注意力门G是当前上下文向量c与注意力结果v通过另一个线性变换得到的.

AOA 机制通过注意力门G对信息向量I添加另一个注意力，应用逐元素乘法得到最终的信息向量，AOA 可建模表示为：

其中，fatt是注意力模块，⊙表示逐元素乘法.

2.4 解码器结构解码器的输入是编码器中所有节点的隐藏层信息egraph、最后时间的节点嵌入elast以及车辆在当前时间t的容量状态和位置lt，给定输入，解码器采用批次搜索采样策略，为了防止生成不合理的路线（例如总路线负载超过车的容量或者重复访问一个客户），设置一个掩码向量来标记已访问的客户节点，确保每个节点在旅行路线中只出现一次，同时节点在下一个时间步长的权重设置为负无穷大.上下文向量Ct在任意时刻t的表达式如下：

其中，fconcat是隐藏层的级联函数，在MHA 中使用获得的上下文向量来获得权重向量.

AOA 计算解码器中时间t的所有节点的上下文向量Ct和隐藏层向量之间的权重，然后将计算出的权重转换为上下文向量并发送到自我注意层.单个输出向量q使用嵌入h0+h0'，…，hn+hn'计算所有动作的输出分布，如下所示：

其中，et表示时刻t的节点隐藏层，mask是标记已访问节点的掩码向量，VB是可训练的参数.

3 训练与推理方法

3.1 模型训练算法在训练阶段，需要花费大量时间来训练网络参数，但当模型训练完成后，可以在测试阶段快速获得预测结果.首先，通过贪婪算法为DHNS 模型提供初始解，DRL 中智能体根据当前环境状态（车的容量或顾客总需求）作出适当的决策，结合奖励机制不断调整参数，直至模型可以修复得到完整解.

模型基于损失函数L来衡量模型操作的有效性，同时使用AC 算法对策略参数进行训练，并利用此算法计算梯度来最大化预期奖励J：

其中，π0为破坏后的解，πt是智能体执行动作a1，a2，a3，…，at-1之后修复的解，基线b(π0)可以有效地减少方差.

模型采用AC 算法进行训练，通过随机策略学习行为网络的参数，行为网络基于概率分布做动作，评判网络基于行为网络生成的行为评判得分，行为网络再根据评判网络的评分调整行为选择的概率.解决VRP 问题的传统策略梯度算法的主要缺点是高维离散空间中不同路径之间的方差大，训练不稳定，但AC 算法可以单步更新，不需要完成整个动作再更新网络参数.传统策略梯度方法对价值的估计虽然是无偏的，但方差较大，AC 算法能够有效降低方差.为了保证策略梯度方差的稳定性，类似于Nazari et al［10］，本文使用评判网络为修复解π0生成一个值c0作为评判网络估算修复的成本，评判网络根据行为网络状态预测奖励值b(π0)，并以预测奖励值b(π0)和实际奖励值L(π0，πt)之间的均值误差作为优化目标.

3.2 模型推理算法基于DRL 策略，为了提高解的精确性，有时仍需要结合传统优化算法（例如波束搜索、采样）进一步提高解的质量.在推理阶段采用批次搜索算法进一步提升解的质量.首先模型采样n条不同的路径作为起始节点，使用贪婪启发式方法为每个轨迹创建初始解，在构建步骤中，所有解决方案都使用成对的破坏和修复运算符进行破坏和修复，最后是为每个解决方案创建一个相邻的解决方案.整个搜索直到达到整个批次的终止标准.

4 数值实验

所有实验均基于Pytorch 1.9.0 深度学习平台，Windows 11 操作系统，使用单张Nvidia RTX 3050 GPU 和i5-11300H CPU 运行本文模型和其他DRL 模型.实验中节点的坐标在[0，1]×[0，1]单位平方形中生成，分别在CVRP20，CVRP50 和CVRP100 上进行训练和测试，车辆的容量限制分别设置为D=30，40，50.DHNS 模型在8 G 显存下运行（100 回合）20，50，100 节点的训练时间分别为11，40 和160 h.最优间隙以LKH3 为基准，其他结果均来自于原文献.聚合函数使用单层的全连接神经网络，批次大小为256，MHA 中的头部H=8，前馈输入层和输出层的维度都是512维，Adam 优化器的学习率为0.0001，权重衰减率为0.95，隐含层设置为128 维.

4.1 CVRP 的实验方案及其模型性能对比实验表1 显示了DHNS 模型求解的CVRP 性能与以前的关键工作进行比较，例如NeuRewriter［19］，NLNS［17］，AM［5］，POMO［13］，DACT［16］，MDAM［20］，DPDP［21］和其他启发式方法.由表1可知，DHNS 模型在推理阶段快于传统算法（LKH3 和CW）以及NLNS，RL（BS），DACT 等模型，优化效果超越目前基于DRL 的模型和专业求解器OR-Tools.与DGTM 比较，DHNS 模型的精度较高，但计算推理时间比DGTM 长，这是由于DGTM 模型属于构造解的模型，模型推理时间较短，而本文模型是改善解的模型，结合传统启发式算法进行搜索，导致推理时间较长，但是解的精度得到保证.进一步分析，模型在CVRP20，CVRP50 和CVRP100 的间隙明显优于目前基于DRL 的方法，与DGTM 相比，CVRP20，CVRP50和CVRP100 的最优间隙分别由原来的0.13%，0.15%和0.19%降低到0.06%，0.09%和0.12%，超越目前基于DRL 的方法.DRL 有希望设计出比启发式规则更好的策略，打破人为设定的限制，智能体自主探索解空间中的最优解.DRL 充分利用同类型问题之间的相似特征，避免传统算法不断重复求解的过程和数据资源的浪费.

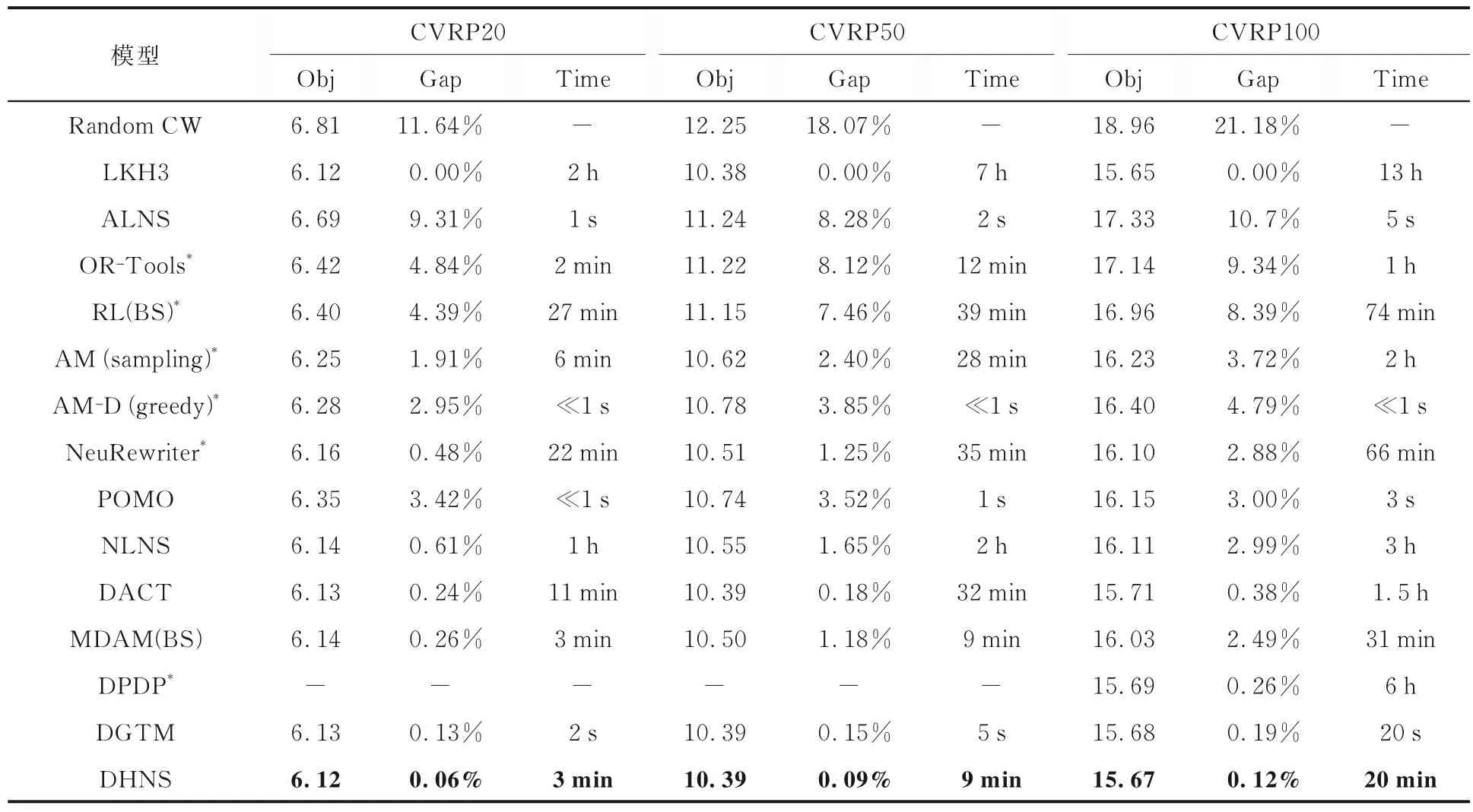
表1 DHNS 模型在CVRP 问题上的优化结果比较Table1 Comparison of CVRP optimization results of DHNS model

DHNS 模型的关键是AOA 在编码和解码阶段发挥着重要的作用，DPE 提取了更多的隐藏和动态的节点结构信息以及贪婪算法提供了较好的初始解.DRL 模型能够自适应地为不同的修复算子分配相应的权重，加速产生更好的解方案.对比ALNS 算法，DRL 能够进一步减少启发式信息的指导和时间成本，能极大地提高算法在解空间的搜索范围.DRL 根据算子的历史表现与使用次数自动选择下一次迭代使用的算子，通过算子间在RL 环境中的相互竞争来生成当前解的邻域结构，这种结构很大概率能够找到更好的解.实验结果表明，与ALNS 结合的DRL 以及AOA 调整后的模型优化性能很好.

4.2 泛化性能及收敛性分析考虑到问题实例会根据模型所作的决策而改变，节点特征也会发生变化，使用AC 算法训练模型的策略有利于网络学习特征.DHNS 模型对求解CVRP 的泛化能力比较如图4 所示.图5 和图6 展示了模型在20节点和50 节点的收敛性.结果表明对于固定的问题大小，DHNS 模型可以很好地推广和解决任何类似规模的问题.更重要的是，尽管CVRP20 需要10 h 的训练，但训练过程仅需一次，并且在推理阶段仅需花费2 min 就可以获得高质量的解决方案，不需要针对不同的问题实例进行再次训练.DHNS 模型具有较好的泛化性能的原因在于DHNS 是基于改善初始解的方式不断提高解，通过ALNS 扩大解的搜索范围，寻求高质量的解决方案，并且通过AOA 防止信息在传输过程中出现误导性信息，更加精确地进行信息传递，进一步提高解的质量.

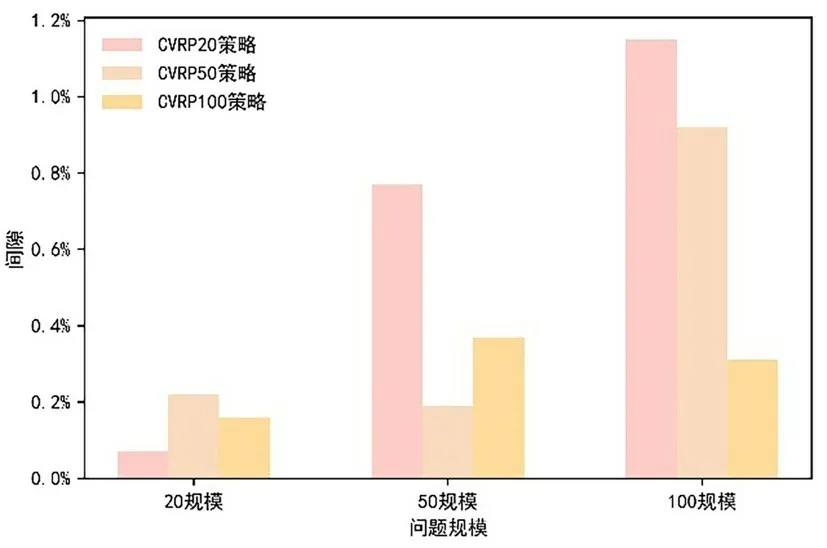
图4 CVRP 泛化性能的比较Fig.4 Comparison of CVRP generalization performance

图5 CVRP20 模型收敛图Fig.5 Diagram of CVRP20 model convergence

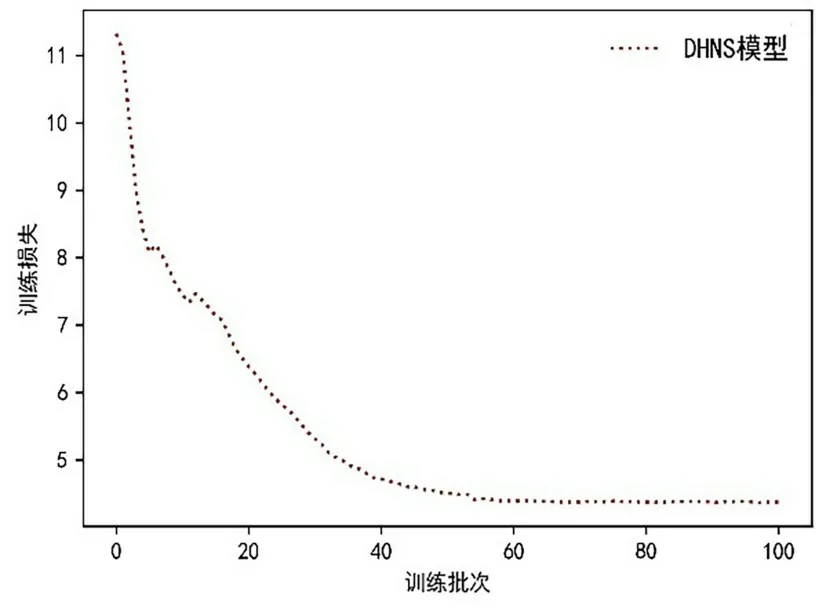
图6 CVRP50 模型收敛图Fig.6 Diagram of CVRP50 model convergence

4.3 真实数据集实例测试本文成功地将DHNS 模型从训练模型推广到现实世界的数据集.表2 是真实数据集CVRPlib 上的22 个实例的实验结果，表中黑体字表示结果最优.由表可见，平均差距进一步缩小到2.89%，证明其差距优于AM，POMO，Wu et al，DACT 和OR-Tools.在混合随机和群集类型以及大多数随机类型的实例上，DHNS 的性能也优于其他基准.鉴于其优势，DHNS 在各种大小和分布的CVRPlib 基准实例上的泛化性能方面优于现有的基于DRL 的模型.

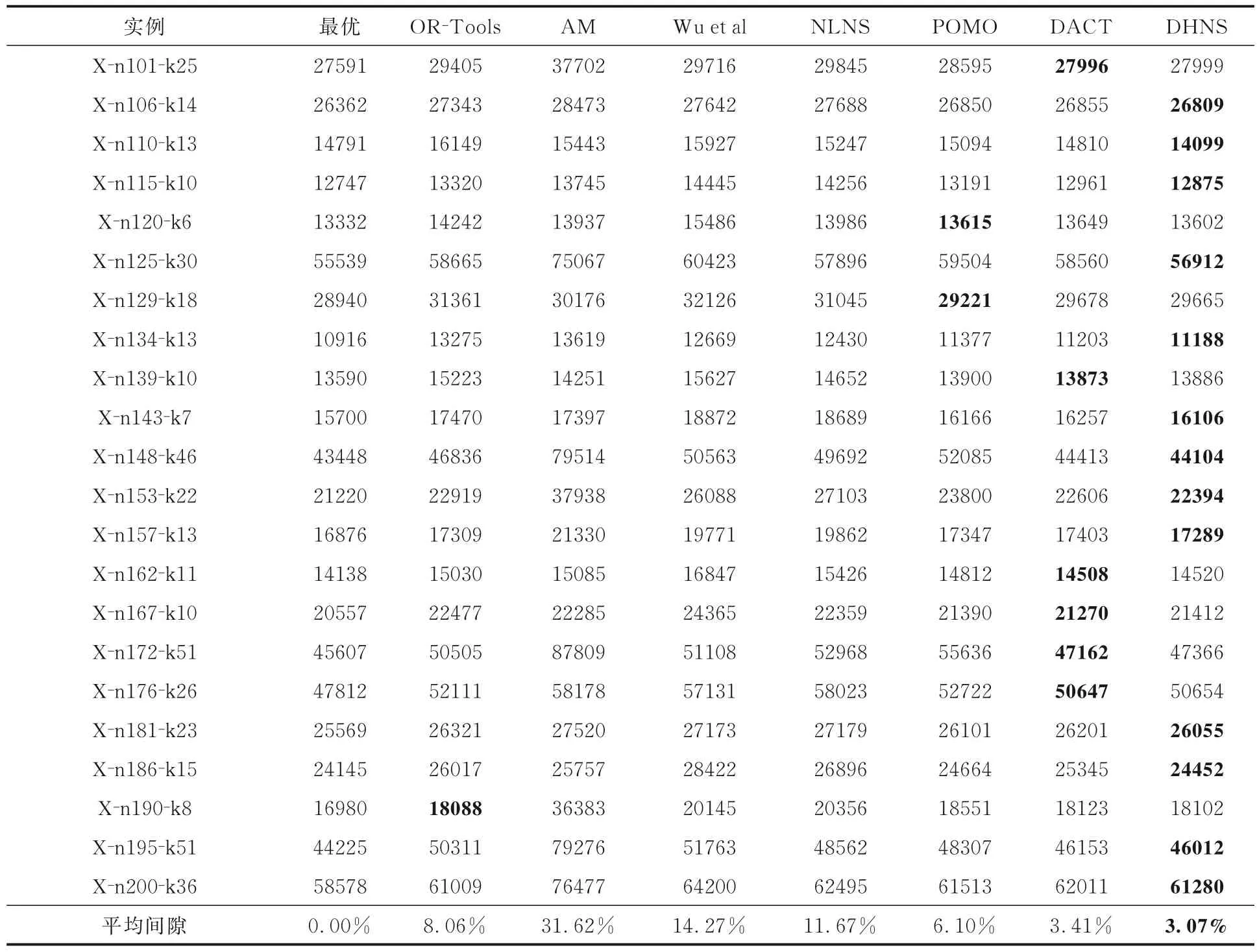
表2 模型在CVRPlib 基准数据集上的实验结果Table 2 Experimental results of the model on the CVRPlib benchmark dataset

4.4 AOA 机制的消融实验为了进一步验证AOA 机制对DHNS 模型的有效性，设计了AOA在编码和解码阶段的消融实验，实验结果如表3所示，表中黑体字表示结果最优.实验结果表明，AOA 可以有效提高DHNS 的优化性能，解决混合模型中可能出现的解码错误，提升解码效率，显著降低CVRP 问题的最优间隙.其中推理时间稍长的原因是AOA 增加了网络层中的参数.

表3 AOA 机制在编码和解码阶段的消融实验Table 3 Ablation experiment of AOA mechanism in encoding and decoding stage

5 结论

本文介绍了一种新的求解CVRP 的深度学习方法DHNS，利用传统启发式与DRL 相结合的混合模型，将AOA 添加到编码器和解码器中，并使用AC 算法来训练Transformer 网络中的参数.在问题规模中等且解精度高的情况下，DHNS 模型非常可取.在保证解的精度的前提下，模型自动从数据中学习启发式方法并使决策过程自动化.实验结果表明，DHNS 模型对100 规模CVRP的优化效果优于现有的DRL 模型和部分传统算法.真实数据集上的测试结果也显示出本文模型的优越性.

未来的工作会首先考虑进一步扩展模型以解决VRP 的其他变体或其他组合最优化问题以及多目标VRP，其次考虑提高基于DRL 方法的解决方案质量.未来主要挑战更有效地处理问题的动态特征，开发更好的机制，使智能体能够了解在访问一个城市后其他城市和环境的变化以及这种动态变化如何影响策略.