基于边界域条件熵的最优尺度约简

金 铭 ,陈锦坤,2* ,孙亚超

（1.闽南师范大学数学与统计学院，漳州，363000；2.福建省粒计算及其应用重点实验室，闽南师范大学，漳州，363000）

Pawlak 粗糙集模型［1］是粒计算的基本模型［2-3］，它利用等价关系将论域划分为若干等价类，每个等价类就是一个知识粒.在Pawlak 粗糙集的理论研究与应用中，属性约简是其中的核心研究内容之一，不少专家学者对传统的属性约简进行研究.近年来，不少文献对基于粗糙集理论的属性约简方法进行总结和比较.例如，赵思雨和魏玲［4］对粗糙集中八种属性约简理论进行分析和讨论，揭示了不同属性约简之间的联系与差异.Zhou et al［5］从基于不同类型决策信息表和不同约简方法的角度出发，对基于粗糙集理论的属性约简算法进行归纳总结.Yuan et al［6］从数据来源、预处理方法、模糊相似性度量、模糊运算、约简规则和评价方法等方面对所有基于模糊粗糙集理论的属性约简方法进行了总结和比较.

上述研究中，每个对象在同一属性下只有一个值，而在现实世界中，每个对象在同一属性下往往有不同的值［7］.例如，学生的考试成绩可以用0～100 的一个自然数记录，也可以用“优秀”“良好”“及格”“不及格”四个等级记录，还可以用是否及格来记录.针对现实世界的这种情况，Wu and Leung［8］提出一种特殊的决策表，即多尺度决策表.而之前这种每个对象在同一属性下只有一个值的决策表又被统称为单尺度决策表.多尺度决策表要求数据表中所有不同的属性都具有相同的尺度个数.在此基础上，Wu and Leung［8-9］提出多尺度决策表的最优尺度选择方法，并分析了最优尺度不同概念之间的关系和给出k尺度约简的定义.魏巍等［10］和郑嘉文等［11］将Shannon 条件熵的概念引入多尺度决策表，探讨在不同的多尺度决策表下熵最优尺度与传统最优尺度的关系.不少学者对最优尺度进一步开展研究［10-13］.例如，为了克服不同属性都具有单一的尺度个数的缺点，Li and Hu［14］提出广义多尺度决策表，并提出最优尺度组合的概念，这种组合方式使不同属性的尺度可能不同.

目前对于多尺度决策表的研究大多集中在最优尺度组合上.Li et al［15］在多尺度决策表中定义了属性重要度的概念，并给出一个基于属性重要度的逐步寻找最优尺度组合的方法.但这种重要度的定义只考虑了同一属性下不同尺度的权重，没有考虑不同属性的权重.张清华等［16］在此基础上将属性重要度与属性代价结合，提出一个基于代价敏感的最优尺度组合选择算法.王金波和吴伟志［17］将似然函数和信任函数引入广义多尺度覆盖决策表中，研究多种最优尺度组合.Wu and Leung［18］给出多种最优尺度组合的定义并探讨多种最优尺度组合的关系.牛东苒等［19］将变精度引入多尺度决策表中，给出多种变精度最优尺度组合定义并探讨它们之间的关系.Cheng et al［20］利用三支决策研究最优尺度组合.Zheng et al［21］利用证据理论进行最优尺度组合.牟琼等［22］给出不完备多尺度决策表下的最优尺度组合.曾华鑫和吴伟志［23］给出不协调多尺度背景下的最优尺度组合的层次关系.现实问题中的决策也是多尺度的.基于此，Huang et al［24］提出广义多尺度决策表.张嘉茹等［25］在协调广义决策多尺度序决策表上定义了五种最优尺度选择并探讨它们的关系.Deng et al［26］与于子淳和吴伟志［27］分别利用三支决策和剪枝思想研究广义多尺度决策表.

Cheng et al［28］在广义多尺度决策表上重新定义尺度组合，由此给出最优尺度约简的定义，但这种约简基于从粗到细的多尺度决策表.对于从细到粗的多尺度决策表，She et al［29］通过粒度树的选择和切割提出广义约简.金铭等［30］将尺度组合进行扩展，给出最优尺度约简的定义.受文献［18，31］的启发，本文首先在从细到粗的多尺度决策表中给出几种最优尺度约简的定义，并考虑在不同情况下给出这几种约简之间的关系.为了进一步给出求解最优尺度约简的方法，引入边界域条件熵的定义，探讨边界域条件熵的性质及与几种约简之间的关系，给出基于边界域条件熵的最优尺度约简算法并用实验验证该方法的有效性.

1 预备知识

1.1 粗糙集基础知识

定义1［1］设非空有限集U为论域，R为U上的等价关系，对于任意X⊆U，X的上、下近似定义为：

其中，[x]R表示对象x在等价关系R下的等价类.

基于上、下近似，给出正域、负域和边界域的定义：

定义2［1］称(U，At)为信息表，其中U={x1，x2，…，xn}为非空有限对象集，称为论域.At={a1，a2，…，am}为非空有限属性集，∀a∈At存在一个满射映射，f∶U→Va，即f(x)∈Va，x∈U.其中，Va={f(x)|x∈U}称为a的定义域.一个二元组S=(U，At∪D)称为决策表，其中(U，At)为信息表，At∩D=∅，At和D分别称为条件属性集和决策属性集.

定义3［1］设S=(U，At∪D)为决策表，对于任意B⊆At，记：

定义4［1］设S=(U，At∪D)为协调决策表，若存在B⊆At，使得RB⊆RD，称B为决策协调集.若B为决策协调集且B的任何真子集都不是决策协调集，称B为协调决策表的决策约简集.

定义5［32］设S=(U，At∪D)为决策表，若U/RD={D1，D2，…，Dr}且B⊆At，x∈U，则给出以下定义：

定义7［31］设S=(U，At∪D)为决策表，B，Q⊆At，条件属性B的划分为U/RB={X1，X2，…，Xm}，B在Q下的边界区域为BNDQ(B)/Q={G1，G2，…，Gt}，B对Q的边界熵和B对Q的边界条件熵分别定义如下：

1.2 多尺度决策表基础知识

定义9［14］称二元数组S=(U，At∪D)为广义多尺度决策表，其中(U，At)为多尺度信息表，D∶U→VD为一个单尺度决策属性.

当每个属性的尺度均为I时，定义9 退化为多尺度决策表的定义.

定义12［30］设S=(U，At∪D)为协调广义多尺度决策表，L'⊆L，K*∈L'.若是协调的且存在K∈L'使得K*≺K，SK是不协调的，则称K*为S中L'的最优尺度组合.若K*是S中L 的最优尺度组合，则称K*为最优尺度约简.

定义13［8］设S=(U，At∪D)为协调多尺度决策表，若第k尺度是协调的，即

是协调的，且第k+1 个尺度是不协调的（若存在k+1），则称k为最优尺度.对于B⊆At，若⊆RD且⊄RD对于任意C⊂B成立，则称B是k尺度约简.

2 多尺度决策表中最优尺度约简

2.1 几种最优尺度约简

若尺度空间L 为Wu and Leung［18］的定义，则定义15 退化为多种最优尺度组合的定义［18］.

2.2 协调广义多尺度决策表下最优尺度约简本节主要研究定义15 提到的几种最优尺度约简在协调广义多尺度决策表背景下的关系.

定理1设S=(U，At∪D)为一个协调广义多尺度决策表，U/RD={D1，D2，…，Dr}，则有以下命题成立：

定理2设S=(U，At∪D)为一个协调广义多尺度决策表，K为尺度组合，则以下条件等价：

（1）K为最优尺度约简；

（2）K为广义决策最优尺度约简；

（3）K为分布最优尺度约简；

（4）K为上近似最优尺度约简；

（5）K为似然最优尺度约简；

（6）K为最大分布最优尺度约简；

（7）K为下近似最优尺度约简；

（8）K为信任最优尺度约简.

证明根据协调多尺度决策表的定义及定理1 易证.

2.3 不协调广义多尺度决策表中几种最优尺度约简之间的关系本节主要研究定义15 中的几种最优尺度约简在不协调广义多尺度决策表背景下的关系.

定理3设S=(U，At∪D)为一个不协调广义多尺度决策表，U/RD={D1，D2，…，Dr}，K为尺度组合，则以下条件等价：

(1)⇔(2) 由定义15 知，∀x∈U，∂AtK(x)=∂At1(x)成立等价于∀x∈U，

定理4设S=(U，At∪D)为一个不协调广义多尺度决策表，K为尺度组合，以下条件等价：

（1）K为广义决策最优尺度约简；

（2）K为上近似最优尺度约简；

（3）K为似然最优尺度约简.

证明根据定理3 易证.

定理6设S=(U，At∪D)为一个不协调广义多尺度决策表，以下条件等价：

（1）K为下近似决策最优尺度约简；

（2）K为信任最优尺度约简.

例1 说明最大分布决策最优尺度约简、分布最优尺度约简与广义决策最优尺度约简并不等价.

例1表1 为广义多尺度决策表，其中U={x1，x2，x3，x4，x5，x6}，At={a1，a2}，I=(2；1)，即L={(1；1)，(2；1)，(3；1)，(1；2)，(2；2)}，则由表1 可计算每个对象在不同尺度组合下的最大分布和概率分布，即表2.

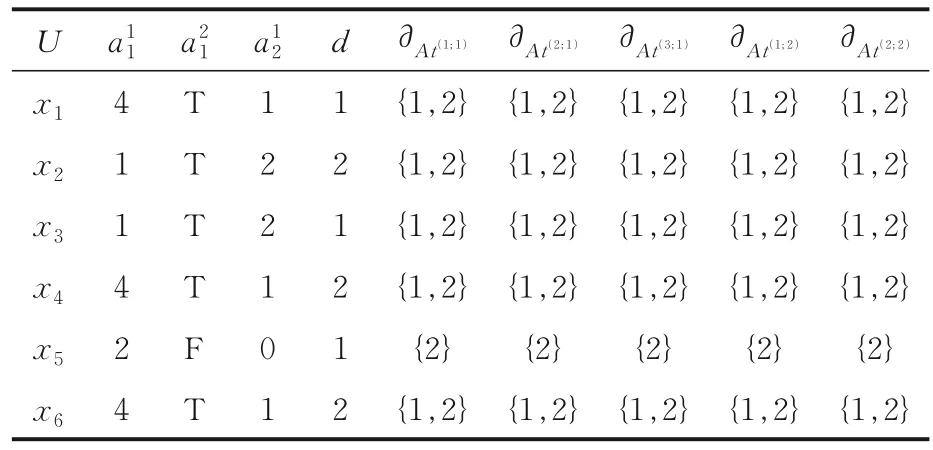
表1 广义多尺度决策表Table 1 Generalized multi-scale decision table

表2 不同对象在不同尺度组合下的最大分布和概率分布Table 2 Maximum distribution and probability distribution of different objects in different scale combinations

显然广义最优尺度约简为(3；1)和(2；2)，而最大分布最优尺度约简为(3；1)和(1；2)，分布约简也为(3；1)和(1；2)，即广义最优尺度约简与最大分布最优尺度约简、分布最优尺度约简并不等价.

例2 说明最大分布广义最优尺度约简与下近似最优尺度约简并不等价.

例2表3 是一个广义多尺度决策表，其中U={x1，x2，x3，x4，x5}，At={a1，a2}，I=(2；1).

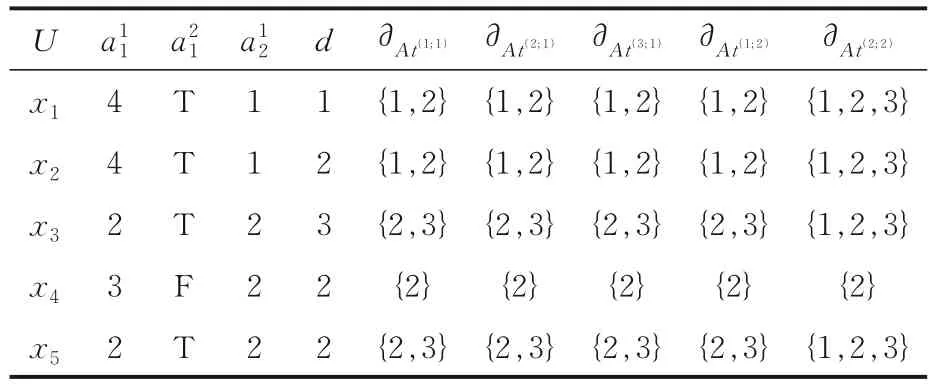
表3 广义多尺度决策表Table 3 Generalized multi-scale decision table

显然广义最优尺度约简为(3；1)和(1；2)，而下近似最优尺度约简为(2；2)，即广义最优尺度约简与下近似最优尺度约简并不等价.

3 基于边界域条件熵的最优尺度约简

3.1 边界域条件熵

定理7设S=(U，At∪D)为广义多尺度决策表，∀X⊆U，K，K*∈L 且K≺K*，则：

对不等式两边取对数得：

且函数f(x)=xlog2x，当x＞0 时是凸函数，根据Jensen 不等式：

3.2 基于边界域条件熵的最优尺度约简本节主要讨论边界域条件熵与多尺度决策表最优尺度约简之间的关系.

3.2.1 协调多尺度决策表的边界域条件熵与约简之间的关系

定理10若S=(U，At∪D)为协调多尺度决策表，以下命题成立：

表4 广义多尺度决策表Table 4 Generalized multi-scale decision tables

当K=(5；2；1)时，

综上，最优尺度约简为K=(5；2；3).

3.2.2 不协调多尺度决策表的边界域条件熵与约简之间的关系

定理11设S=(U，At∪D)为一个不协调广义多尺度决策表，以下条件等价：

证明根据定理3 和定理9 证明可得.

定理12设S=(U，At∪D)为一个不协调广义多尺度决策表，以下条件等价：

（1）K为广义决策最优尺度约简；

（2）K为上近似最优尺度约简；

（3）K为S的似然最优尺度约简；

证明根据定理9 易证.

根据定理12，给出基于边界域条件熵的最优尺度约简算法.

对于每个尺度组合，求其边界域条件熵的时间复杂度为O(|U|).在最坏的情况下，循环需要遍历每个可能的尺度，此时，步骤3～4 的时间复杂度为算法总的时间复杂度为

若步骤4 中1 ≤j≤Ij，即尺度组合K∈L1，则该算法退化为求最优尺度组合的算法.此时算法总的时间复杂度为

3.3 实验结果为了客观地评价利用边界域条件熵求最优尺度约简的有效性，本文采用开放的UCI 数据集进行验证.由于UCI 中数据集都为单尺度数据且数据集中存在缺失值，因此需要对UCI 数据集进行处理，处理方式如下，处理后的数据如表5 所示.

表5 预处理后的UCI 实验数据集Table 5 Preprocessed UCI datasets for test

（1）删除单尺度数据表中的缺失值，同时将其中的非数值元素用“1，2，…”等代替.

（2）对于每个属性a，计算它的标准差、最小值和最大值，并分别用δa，ma和Ma表示.a(x)表示对象x在属性a处的取值.令k=，其中[·]表示取整.对象在属性a第一尺度上的值按照标准差δa进行等分离散化.

（3）在第一尺度的基础上，通过从上到下合并某个值，直到当前尺度中的等价类数不超过三个，得到属性的这些后续尺度.增加一个新的尺度只会合并前一个尺度的一个值.例如，将上一尺度属性值为1 和2 的等价类合并成下一尺度属性值为2 的等价类.这样就得到了一个广义多尺度决策表.

实验采用的编程语言为Matlab R2016a，PC 系统为Windows 7，CPU为Inte（rR）Core（TM）i7-6700 CPU@3.40 GH 以及8G 内存.

为了客观验证算法的有效性，比较四种算法Lattice model［14］，SOSC［15］，BOSC 和算法BOSR的差异性，其中算法BOSC 表示算法退化后求最优尺度组合的算法.

实验过程中，当数据集基数的大小增加时，四种算法的实验结果如图1 所示.采用十折交叉验证，将数据分成十份，横轴表示选取数据占据样本数据的比例，纵轴表示运行时间.整个数据集的运行时间如表6 所示，表中黑体字表示在每个数据集上最短的运行时间.

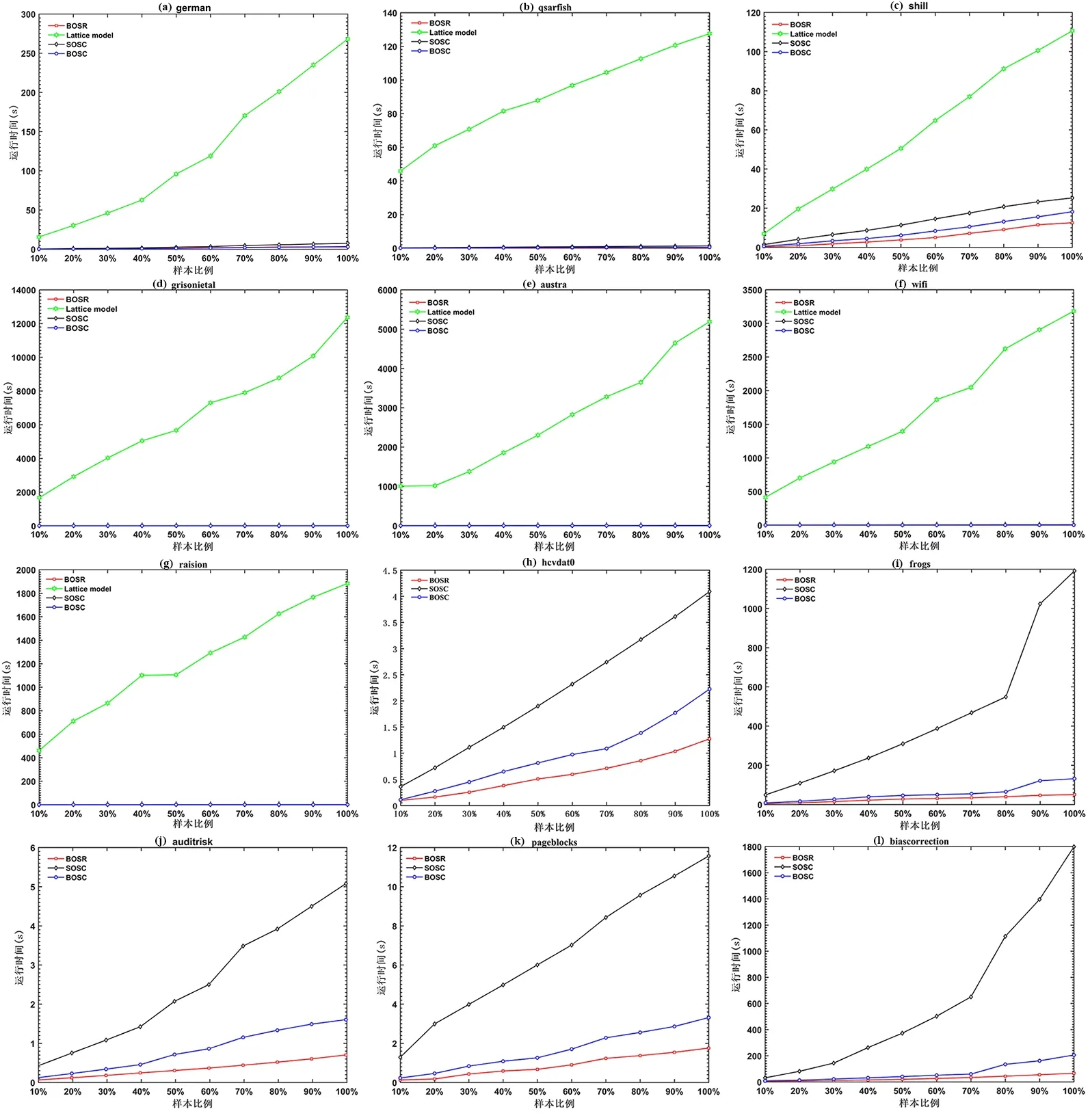
图1 不同数据集下算法的运行时间Fig.1 Running time of algorithms in different datasets

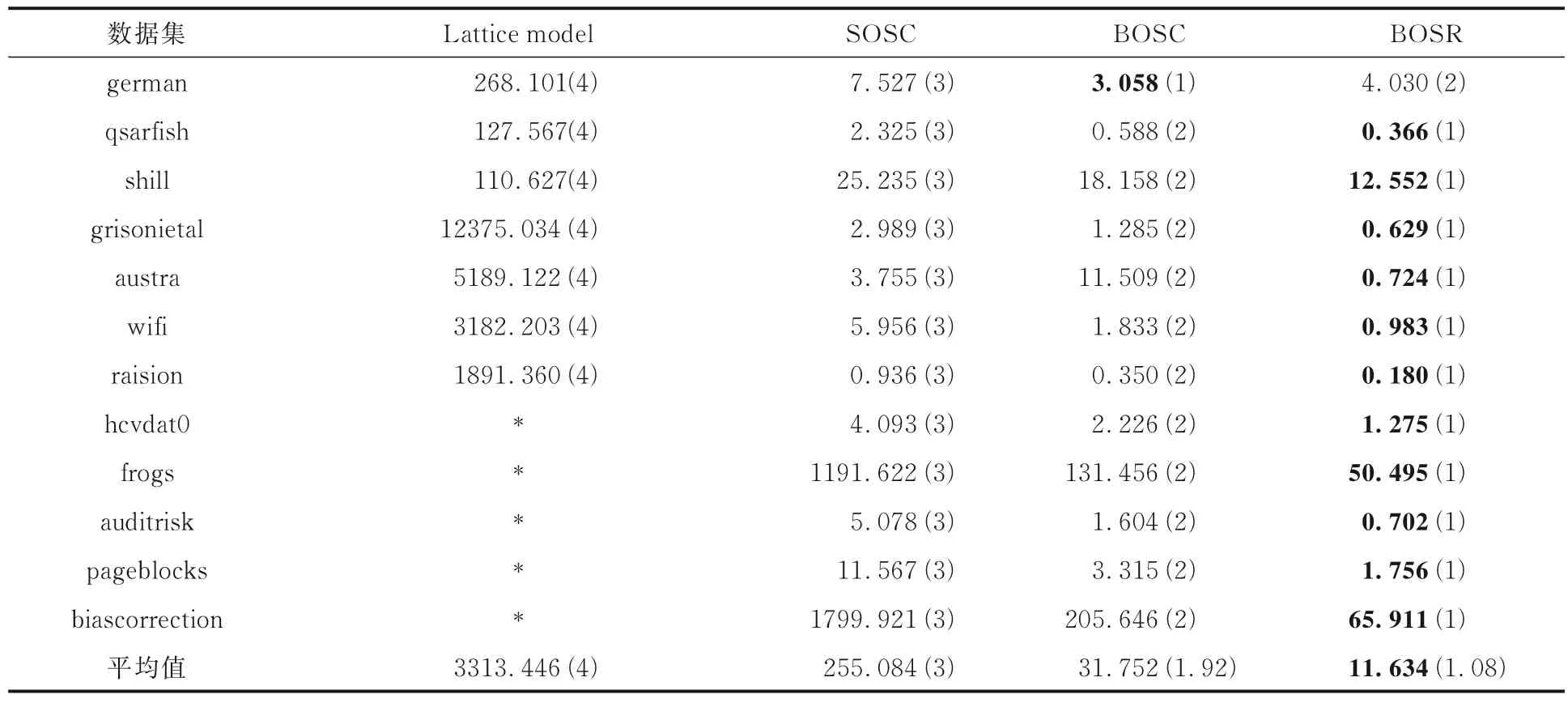
表6 四种算法在不同数据集下的运行时间(单位：s)Table 6 Running time of four algorithms under different datasets (unit:s)

从表6 可以看出，当数据集属性个数较多或尺度较大时，算法Lattice model 不能运行.当算法Lattice model 可以运行时，该算法的运行时间最长.在大部分数据集下，算法BOSR 的运行时间都低于其他三种算法.从图1 可以看出，当数据集基数的大小增加时，四种算法的运行时间也都不断增加.但算法Lattice model 的增长速度明显高于其他三种算法.而算法BOSC 的增长速度明显高于算法BOSR.

由于部分实验数据属性数目过大，为了方便展示，仅选取属性数目较少的数据结果进行展示，见表7.从表7 可以看出，对于部分数据而言，最优尺度组合和最优尺度约简是一致的；对于一些数据而言，四种方式的结果是相同的，而对于部分数据而言，由于SOSC 求得的为其中一个最优尺度组合，因此与算法BOSC 求得的结果并不相同.

表7 四种算法在部分数据集上的结果展示Table 7 Results display of four algorithms on partial datasets

为了进一步验证实验结果的差异性，引入统计测试.首先用Friedman 测试来检测不同算法之间是否存在显著性差异.在零假设情况下，计算Friedman 统计值：求得算法BOSR 在时间下的值约为240.454.而四种算法和12 个数据集的临界值F(12-1，(12-1)×(4-1))=F(11，33)在α=0.1 下取值2.840.因此算法间存在显著差异，进一步用Bonferroni-Dunn 来比较不同算法间性能的差异.当k=4 时，q0.10=2.218.因此，CDα=1.121.

图2 显示了对12 个数据集进行α=0.1 的Bonferroni-Dunn 检验结果.由图可见，在时间上，算法BOSR 与算法BOSC 的平均距离小于1.121，与另外两种算法的平均距离均大于1.121.因此，算法BOSR 与算法BOSC 没有显著差异，与另外两种算法具有显著差异.同理可知，算法SOSC 与算法BOSC 没有显著差异；算法Lattice model 与算法SOSC 没有显著差异.

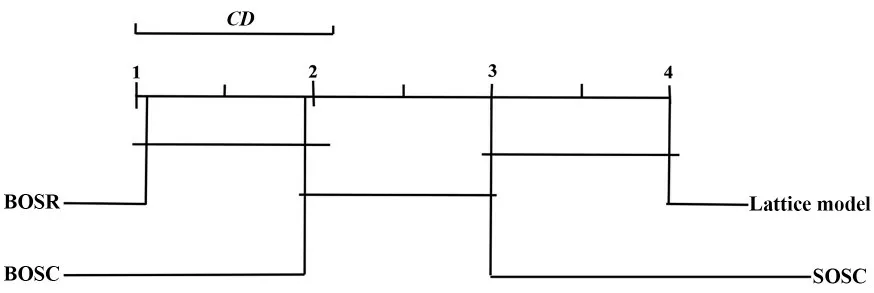
图2 用Bonferroni-Dunn 检验比较BOSR 算法与其他算法的性能Fig.2 Bonferroni-Dunn test was used to compare the performance of BOSR algorithm with other algorithms

4 结论

本文将粗糙集中的一些约简定义扩展到多尺度决策表中，并给出几种最优尺度约简之间的关系.然后将边界域与条件熵结合，在多尺度背景下提出边界域条件熵的定义.考虑边界域条件熵与几种约简之间的关系，给出利用边界域条件熵求最优尺度约简的方法，并通过实验证明该方法的有效性.但本文没有考虑如何利用边界域定义互信息熵的概念.因此，如何利用边界域给出互信息熵的概念也是一个值得思考的问题.