基于模态控制法的平板扬声器指向性控制算法研究

卫文港,程嘉正,冯雪磊,沈 勇

（近代声学教育部重点实验室，南京大学物理学院，南京，210023）

平板扬声器指一种使用单个或多个激励器驱动薄板产生弯曲振动从而发声的扬声器类型［1］.相比于传统的动圈式扬声器，平板扬声器具有更好的集成性，无须额外的出声孔，在手机、电视机等追求超薄结构的设备中很有优势，近年来，OLED 屏幕的普及大大提高了屏幕发声技术的可行性［2-3］.基于平板扬声器的屏幕发声所辐射声波的主瓣位于屏幕的正前方，而传统的内置扬声器系统，由于出声孔的限制，声波只能从屏幕的侧边发出，其所辐射声波的主瓣更多位于屏幕所处的平面内.这一特点使得屏幕发声更适用于结合声投射技术进行空间声重放.声投射技术指通过控制一个紧凑型声系统（手机、电视机等属于该类型声系统）的声辐射指向性，形成相应的波束，波束经过壁面的一次反射到达听者.通过控制声系统的指向性，产生不同的波束，即可产生多个虚拟声源，从而达到使用一个紧凑型声系统完成空间声重放的目的.目前已有将该技术应用于电视机的内置扬声器系统的实例［4］，但尚未发现将模态控制法应用于平板扬声器指向性控制的研究先例.声投射技术的核心，在于控制声系统的指向性，形成定向波束.因此，有必要对平板扬声器的指向性控制进行研究.

2017 年Anderson et al［5］基于薄板振动的模态行为更新了平板扬声器的仿真模型，考虑了薄板尺寸以及后腔的影响，并在模型搭建时考虑到了多个激励器间的耦合.平板扬声器的控制主要分为针对振动的控制和针对声辐射的控制.

平板扬声器的振动控制具有较为丰富的研究基础，因为板的振动控制一直是工程领域的一个重要研究课题［6-9］.早期研究中，平板扬声器的振动控制是通过在特定位点附加质量或弹簧质量系统实现的［10-13］.2016 年Anderson et al［14-16］提出一种模态交叉网络的控制方法，由于薄板的振动可以视为无数个模态振型的叠加，通过控制前几个模态的激励幅度及相位，实现只激发特定模态，或同时激励多个模态，使其叠加获得期望的振动响应，可以在低频段实现对振动的主动控制.相关研究表明，在高频段，薄板的模态分布足够密，由于模态间的相互堆叠，薄板的振动会明显地聚集在激励点附近，薄板的模态行为明显减弱，模态方法在高频的作用效果也会大大降低［17］.

相比于振动控制，针对平板扬声器声辐射控制的研究不多.由于平板扬声器的模态行为，其频响曲线在低频容易出现较大的峰谷，即使在高频也会有许多小峰谷.为此，Bai et al［18-19］基于数学规划的方法对平板扬声器的设计参数进行了优化，得到平滑的频响曲线，同时更接近于全指向性.在指向性控制方面，早期曾有研究使用多个单激励器驱动的平板扬声器进行波场合成（Wave Field Synthesis，WFS）［20］，但相邻板之间激励器的间距会在高频造成混叠，而低频受到模态行为的影响，WFS 的效果也会较差.为修正上述缺点，采用多激励器驱动的平板扬声器，可以有效降低高频声波混叠的影响，虽然实验效果和前者比较有提升，但是在低频，仍然存在模态行为及激励器之间互相耦合的影响，导致控制效果较差［21］.最近，出现使用声对比度控制算法（Acoustic Contrast Control，ACC）研究平板扬声器的指向性控制［22-23］.该方法将不同角度划分为明区与暗区，并通过施加滤波器使辐射声能尽可能集中于明区.但是，该方法无法控制声波在明区的分布，可能会在明区造成严重的幅度和相位失真，在明区范围较大的情况下，失真尤其严重，影响听者的听感，因而局限了该方法的应用.

本文主要研究了平板扬声器的指向性控制.目前，关于使用平板扬声器实现任意指向性的相关研究较少，仅有基于WFS 方法［20-21］和基于ACC 方法的研究［22-23］.为进一步完善该领域的理论研究，本文从模态控制法出发，对平板扬声器的指向性控制开展理论研究.结合数值仿真，进行方法的可行性验证以及后续的参数化分析.

1 平板扬声器波束形成理论模型

平板扬声器是由激励器驱动薄板，产生弯曲振动，进而辐射声能的扬声器.本节首先介绍平板扬声器的物理模型，包括激励器、薄板的弯曲振动与声辐射三部分；再介绍评价指向性控制的关键性能指标［24-26］；最后介绍利用模态控制法实现平板扬声器指向性控制的理论.

1.1 平板扬声器声辐射理论平板扬声器用动圈式激励器的等效电路演示（图1）.

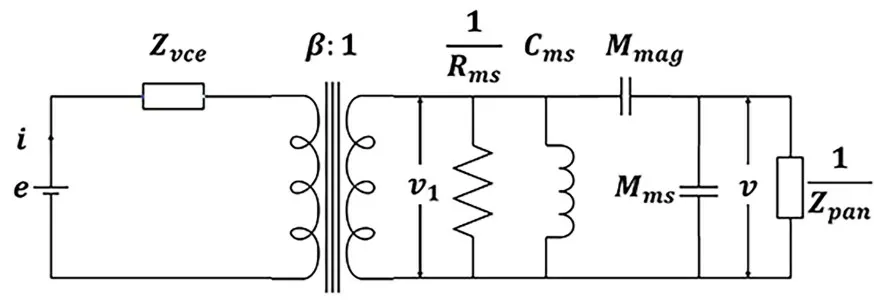
图1 激励器等效电路图Fig.1 Exciter equivalent circuit diagram

其中，e为激励器输入电压，i为流经激励器电路的电流，Zvce为激励器电路部分的电阻抗，β=Bl为激励器磁回路的力因子，Cms为激励器悬置系统的力顺，Rms为激励器悬置系统的力阻，v1为流经Cms和Rms的速度，Mmag为磁铁的质量，Mms为激励器悬置系统的振动质量，Zpan为薄板给到激励器的力阻抗，v为激励器振膜的振动速度，即薄板受激励点的振动速度.基于图1，可得激励器输入电压e，激励器电路的电流i，激励器振膜的振动速度v和薄板受到的激励力F之间的方程为：

其中，s=jω为复频率，ω为角频率.根据式（1）～（4），可得激励器输入电压e与激励器振膜的振动速度v和薄板受到的激励力F之间的物理关系为：

式（6）中的Zpan为未知量，受到薄板本身物理特性的影响，且有可能受到其他激励器的影响，Zpan在本文中是中间变量，在已知输入电压e和激励器振膜的振动速度v以及Mms等参数时，可以根据式（5）理论计算得到Zpan.

关于薄板的弯曲振动已有较为丰富的理论研究［27］，本文以各向同性结构化损耗因子η的形式引入阻尼，引入阻尼后薄板弯曲刚度D0变为：

基于Kirchhoff 板振动理论，直角坐标系中各向同性薄板弯曲振动方程如下：

其中，w为薄板弯曲振动位移，ρ为薄板的密度，τ为板厚度，F为施加在薄板上沿z方向的外力.

在远场时薄板振动的辐射声场可以积分计算［28］：

其中，rp为辐射空间中某点的坐标，p(rp)为空间中一点的声压，r为平板上某点的坐标，w(r)为平板上某点位移，ρ0为空气的密度.

1.2 指向性控制关键性能指标指向性控制的关键指标包括声对比度、匹配误差、阵列效率.定义pb和pd分别为明区Lb个采样点声压向量和暗区Ld个采样点声压向量，声对比度定义为明区和暗区内的平均声能之比，即：

其中，上标H为共轭转置运算符.

匹配误差反映了进行波束形成后重放声与目标声的误差大小，假设p为重放声场采样点声压向量，pdes为目标声场采样点声压向量，匹配误差定义为重放声压与目标声压之间误差的平方和与目标声压平方和之比，即：

匹配误差越小，代表重放声与目标波束越接近.

阵列效率反映了扬声器阵列为实现重放声场效率的高低，定义为重放声场与参考声场总能量之比，其表达式可以写为：

其中，e为输入电压向量，p为在输入为e时的重放声场采样点声压向量，eref为参考输入电压向量，向量元素全部为1 V，pref为输入为eref时参考声源重放声场采样点声压向量，阵列效率越低意味着产生相同重放声场能量需要更高的输入.

1.3 基于模态控制法的平板扬声器指向性控制算法频率f处，在Ls个驱动力作用下，薄板的弯曲振动方程可写作：

假定薄板的位移w(x，y)可以用无限多个正交的模态来表示，即：

其中，Am为每个模态的激励大小，Φm，n(x，y)为对应模态的振型函数，下标m对应x方向上的模态阶数，下标n对应y方向上的模态阶数.模态Φm，n(x，y)的振型函数由平板扬声器的边界条件决定.如在经典的简支边界条件下模态的振型函数可写作：

不同边界条件下模态振型函数已有相关研究［29-31］.将式（15）代入式（14）中，计算得到：

为简便起见，下文中仍将下标m0和n0写作m和n.即可得到驱动力与模态大小之间的关系为：

将式（18）写作矩阵形式，则：

其中，下标B代表共选取了B个模态，Φ为耦合矩阵，代表了驱动力作用点与各模态之间的耦合特性，Zmode为模态阻抗矩阵，为一对角阵，其对角线上的值为各模态的阻抗大小.参考式（4）～（6），关于第ls个激励器的表达式为：

整理后得：

vls为每个激励点位的振动速度，可表示为：

式（23）写成矩阵形式，则：

将式（24）写成矩阵形式，则：

联立式（19），（25）和（29），得：

因而得到传递函数：

假设目标的模态激励大小为ades，指向性控制的目标为使重放模态激励大小a尽可能接近于目标模态激励大小ades，则需使a与ades之间的距离最短，即最小化二者之差的平方.如此，可得式（32）所示的数学规划问题：

其中，τ为正则化参数，起到提高算法效率和算法鲁棒性的作用.求解式（32），可得：

式（33）表明了如何施加驱动电压，使所选取的模态激励a尽可能接近目标模态激励ades.这是首次不将激励器当作力源，得到的关于平板扬声器的传递函数公式.

将模态控制法应用于平板扬声器的指向性控制，关键在于如何得到目标模态激励ades.由于平板的位移是不同模态振型的叠加，其辐射的声压也可以是不同模态辐射声压的叠加，由式（9）可得：

其中pm，n(r)为对应模态振型函数产生的辐射声压.将式（34）写作矩阵形式，则：

其中，

Gmode为不同模态激励到辐射声压的传递函数.亦可得式（37）所示的数学规划问题：

ades即为式（33）所示的数学规划问题之解，求解式（37）可得：

本小节描述了如何计算得到目标模态激励ades，根据不同的目的有不同的计算方法，得到ades后，可基于式（33）计算得到激励器阵列的输入电压e.

2 平板扬声器波束形成数值仿真

为了验证平板扬声器模态控制法波束形成效果，本节进行数值仿真，首先研究算法控制波束主瓣轴向的和覆盖角的效果，然后探究模态数量、激励器数量两个参数对算法的影响，最后对算法的鲁棒性进行了实验与分析.

2.1 模型设置数值仿真在频域进行，薄板用MATLAB 建模，薄板的尺寸如图2 所示，其中板使用电子设备屏幕常用的玻璃材质，参数为杨氏模量E=73.6 GPa，泊松比ν=0.23，密度ρ=2380 kg·m-3，各向同性损耗因子η=0.1.

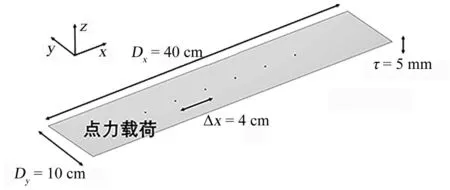
图2 薄板仿真示意图Fig.2 Schematic diagram of thin plate simulation

激励器的位置均匀分布在板对称轴上，间距为2 cm.

为验证模态法能够有效控制平板扬声器声辐射指向性，首先基于1.3 建立激励电压e计算模型，使用前200 个模态进行计算.边界条件设置为简支，在xz平面距离板中心五倍板长的半圆上取角度间隔为 10°的 19 个点，坐标为(-5Dx，0，0)的点的角度定义为-90°，坐标为(5Dx，0，0)的点的角度定义为90°，作为计算作用力与声压传递函数的声压采样点，近似为远场声压，声压向量记为：

为了计算pG与激励器输入电压之间的传递函数G，依次将第ls个激励器的输入电压设置为1 V，计算采样点声压记为：

于是对应频率的传递函数矩阵G为：

已知传递函数矩阵G与目标声压pdes，可基于式（33）和式（38）计算所需的激励器电压edes.其中计算传递函数G时，当它的条件数小于1×1012时，设置正则化参数λ为零；如果条件数大于1×1012，设置初始正则化参数为1×10-20并以10倍逐步加大，直到传递函数G满足条件数小于1×1012.

下一步，建立声重放模型.为了让模型尽量接近真实物理场景，尽可能使用更多模态.计算最高共振频率为196 kHz，对应第476 个模态，选取前476 个模态建立重放模型.将计算得到的激励器电压输入到重放模型中进行仿真验证，在xz平面距离板中心五倍板长的半圆上取角度间隔为5°的37 个点，作为重放声压采样点，用于计算评估指向性控制效果的性能指标，声压向量记为：

2.2 控制波束主瓣轴向和覆盖角为了验证模态控制法能够控制平板扬声器的波束主瓣轴向和覆盖角，设定薄板基本参数、声压采样点以及正则化参数设置与2.1 节相同，设定频率范围为100～4000 Hz，目标覆盖角为20°，边界条件为简支，使用前200 个模态进行仿真.设定不同目标波束主瓣轴向分别为0°，30°，60°，仿真结果如图3 所示.由图3 可以看出利用模态控制法能够精确地控制平板扬声器声辐射波束主瓣轴向.

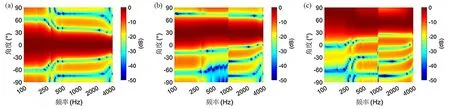
图3 不同波束主瓣轴向等值线图，波束主瓣轴向：(a) 0°；(b) 30°；(c) 60°Fig.3 Contour diagrams of different beam main lobe axis directions，beam main lobe axis direction：(a) 0°，(b) 30°，(c) 60°

为验证模态控制法控制覆盖角的效果，设定目标波束主瓣轴向为0°，设定目标覆盖角分别为20°，80°，140°，仿真结果如图4 所示.由图4 能够看出利用模态控制法能控制平板扬声器覆盖角，频率越高覆盖角控制得越精确.

图4 不同覆盖角等值线图，覆盖角: (a) 20°；(b) 80°；(c) 140°Fig.4 Contour diagrams of different coverage angles，coverage angles：(a) 20°，(b) 80°，(c) 140°

2.3 模态数量由1.3 平板扬声器的位移w(x，y)可以用无限多个正交的模态来表示，在使用模态控制法进行波束控制时，模态使用数量是我们关心的问题.设定薄板基本参数、声压采样点以及正则化参数设置与2.1 相同，本小节分别使用前6，24，200 个模态进行波束控制，波束主瓣轴向为0°，覆盖角为20°，结果如图5 和图6 所示.由图5 和图6 能够看出，随模态数量增加，声对比度升高，匹配误差降低，阵列效率降低，意味着控制产生的波束性能变好.

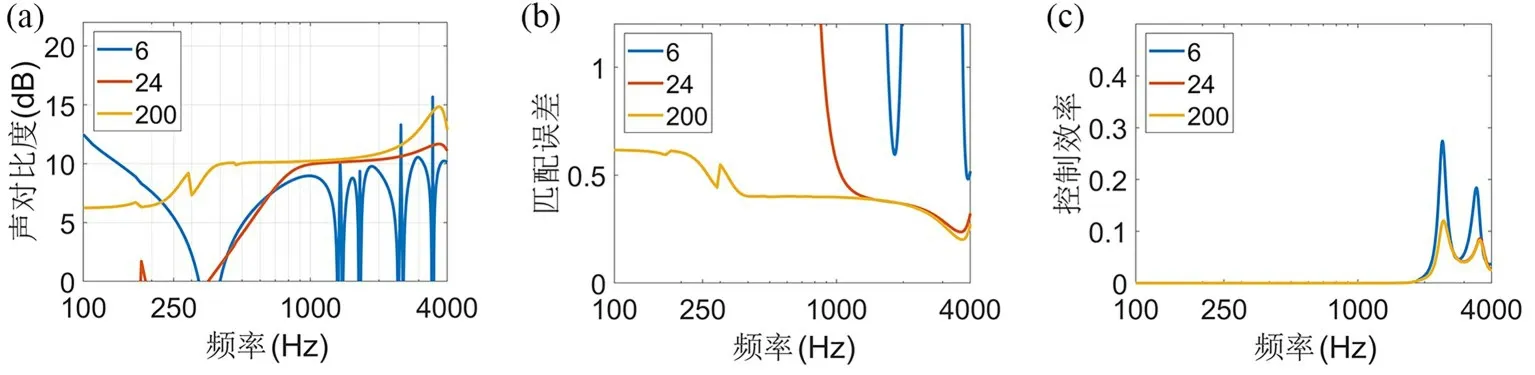
图6 不同模态数量的性能指标：(a)声对比度；(b)匹配误差；(c)阵列效率Fig.6 Performance indicators for different mode numbers：(a) acoustic contrast，(b) matching error，(c) array efficiency

2.4 激励器数量激励器驱动平板扬声器振动，由1.3 可知，由于线性叠加原理，当板受到多个点力作用时，平板的位移w为各驱动力单独作用时的位移之和，因而激励器的数量对波束形成的影响值得探究.设定薄板基本参数、声压采样点以及正则化参数设置与2.1 相同，设置波束主瓣轴向为0°，覆盖角为20°.激励器等间隔分布在薄板中心两侧，当使用的激励器数量分别为2，4，6，8，10 时，仿真结果如图7 和图8 所示.

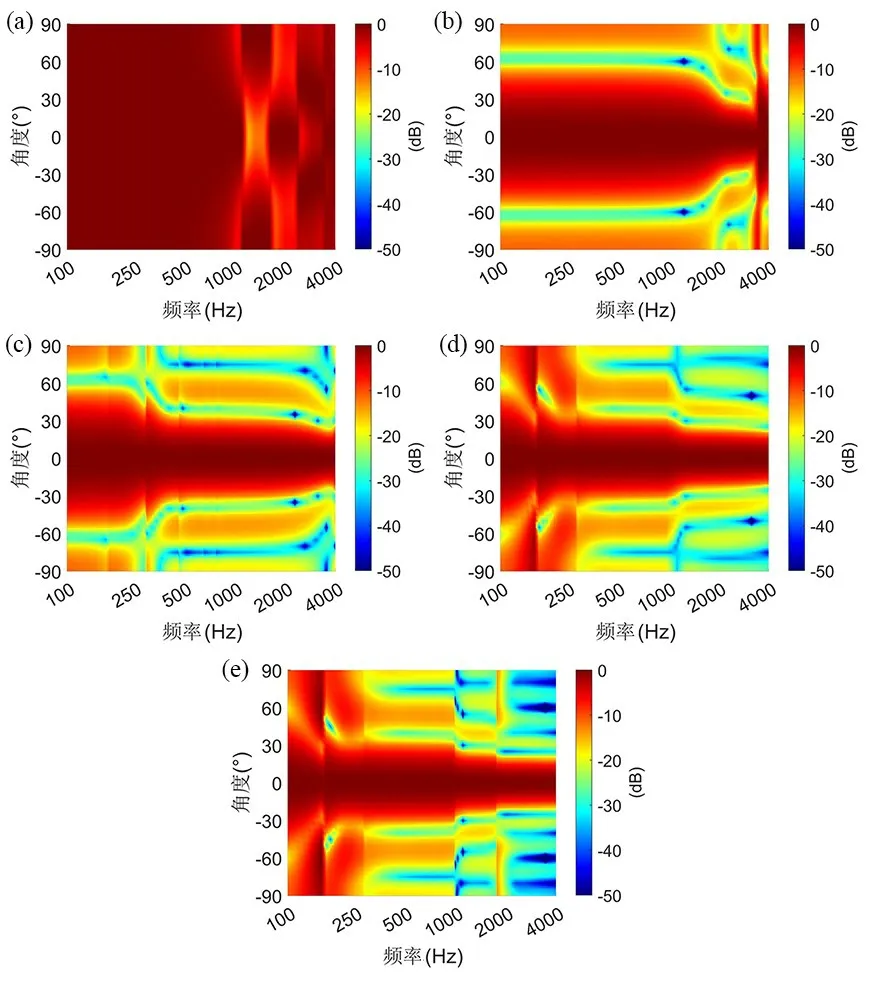
图7 不同激励器数量计算结果，激励器数量:(a) 2；(b) 4；(c) 6；(d) 8；(e) 10Fig.7 Calculation results of different exciter numbers，the number of exciters：(a) 2，(b) 4，(c) 6，(d) 8，(e) 10

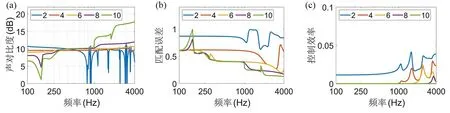
图8 不同激励器数量的性能指标：(a)声对比度；(b)匹配误差；(c)阵列效率Fig.8 Performance indicators of different exciter numbers：(a) acoustic contrast，(b) matching error，(c) array efficiency

由图7 和图8 能够看出，随激励器数量增加，模态控制法在低于300 Hz 时声对比度降低，高于300 Hz 时声对比度升高，在全频域内匹配误差和控制效率降低.总体控制效果变好.

2.5 鲁棒性分析在实际应用场景中，平板扬声器的参数可能会有误差，本小节研究了激励器位置发生偏移时的波束形成效果.设定薄板基本参数、声压采样点以及正则化参数设置与2.1 相同，对其中某一激励器位置误差分别设为无误差，10-6m，10-5m，10-4m，10-3m，10-2m 时，仿真分析波束形成效果，仿真结果如图9 和图10 所示.

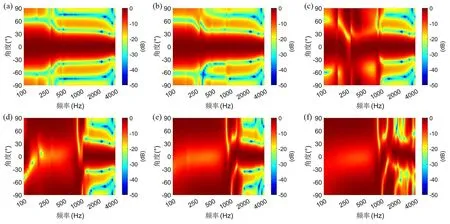
图9 激励器位置误差：(a) 无误差；(b) 10-6 m；(c) 10-5 m；(d) 10-4 m；(e) 10-3 m；(f) 10-2 mFig.9 Actuator position errors：(a) no error，(b) 10-6 m，(c) 10-5 m，(d) 10-4 m，(e) 10-3 m，(f) 10-2 m

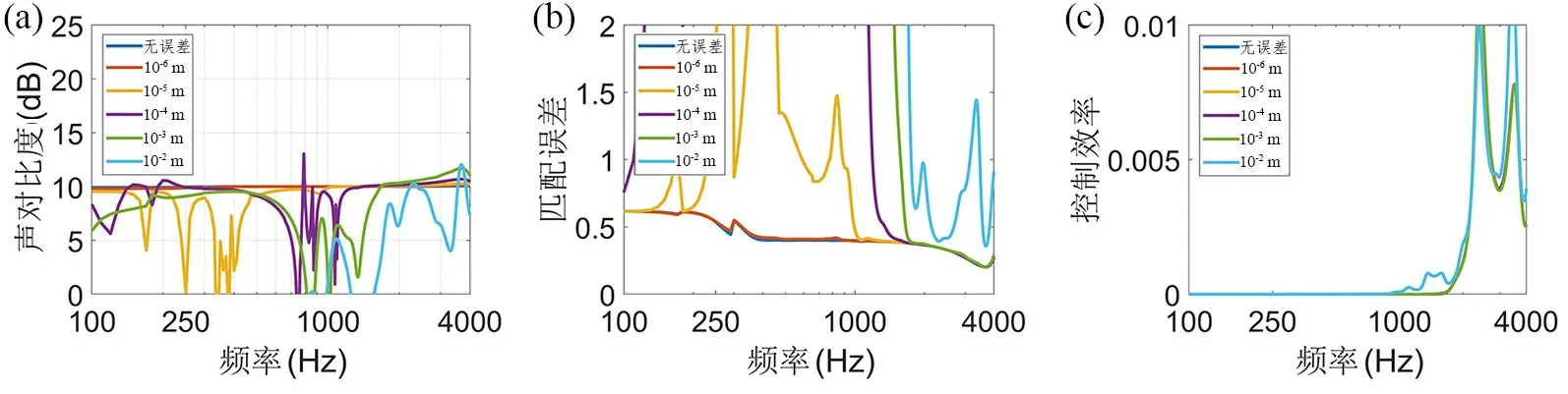
图10 激励器位置不同误差的性能指标：(a)声对比度；(b)匹配误差；(c)阵列效率Fig.10 Performance indicators of actuator position with different errors：(a) acoustic contrast，(b) matching error，(c) array efficiency

由图9 和图10 能够看出，激励器位置误差为10-6m 时，声对比度、匹配误差、阵列效率变化较小，有较好的鲁棒性.当激励器位置误差大于10-6m 时，控制效果明显变差.

3 结论

指向性控制是实现定向发声的关键，尚未发现将模态控制法应用于平板扬声器指向性控制的研究先例.本文创新性地引入模态控制法对平板扬声器指向性进行控制，推导了激励器阵列到辐射空间中各点的传递函数，给出了波束形成所需激励的计算方法.通过数值仿真对其进行验证，结果表明，模态控制法具有显著效果，能够精确控制波束主瓣轴向，在高频时能够更精确地控制覆盖角.本文对模态数量、激励器数量、算法鲁棒性进行了分析.结果表明，模态数量增加时，控制产生的波束性能变好；激励器数量增加时，总体控制效果变好；模态控制法在激励器位置误差低于10-6m 时有较好的鲁棒性，当激励器位置误差量级大于10-6m 时，控制效果明显变差.因而，本研究可为平板扬声器的部分参数设置提供指导.

本文的进一步工作包括设计组装实物进行实验与分析、与数值仿真比对分析等.