融合时间的单温度敏感点机床热误差建模方法
2023-12-12唐光元苗恩铭王文辉石照耀
唐光元,苗恩铭,王文辉,石照耀
(1.重庆理工大学 机械工程学院, 重庆 400054) (2.北京工业大学 北京市精密测控技术与仪器工程技术研究中心, 北京 100124)
0 引言
数控机床的热特性是机床性能的重要指标之一,而数控机床的热误差是机床热特性的具体体现。热误差对数控机床尤其是高精度数控机床的精度有重要影响,可占总误差的40%~70%[1-3]。因此,获得最优的数控机床热特性在生产制造中有重要意义。目前,国际上大多通过提高热误差补偿模型的预测效果进行优化[4],涉及热误差数据处理方法等多项研究内容[5]。
对于热误差预测补偿模型的研究始终是国际热点。Li等[6]使用不同聚类方法选择温度敏感点,通过抑制温度点之间的多重共线性和选择多元回归来构建热误差模型,提高了误差模型的预测精度和鲁棒性。Wei等[7]基于最小二乘法,在每个时间点建立与工作台的二维热误差模型,提高了工作台的热误差补偿效果。Mareš等[8]针对五轴机床的热误差补偿,使用传递函数模型与多元线性回归模型进行比较,通过传递函数模型显著减少了机床X、Y和Z三个方向的热误差。Liu等[9]采用岭回归算法建立热误差模型,通过抑制共线性,降低模型对热误差预测带来的不良影响,提高长期预测精度。Zhang等[10]将支持向量机进行在线训练,实时预测机床热误差,并与BP神经网络比较,证明支持向量机具有补偿精度高、泛化能力强的特点。Yao等[11]综合灰度模型与最小二乘支持向量机的优点,提出了一种新的热误差预测复合模型,在热误差预测方面准确性更高。Li等[12]利用偏相关分析识别温度敏感点,并基于加权最小二乘支持向量机计算机床主轴的热误差模型,证明该方法具有较高的精度和鲁棒性。谭峰等[13]提出一种基于长短期记忆循环神经网络的数控机床热误差预测方法,在不同工况下与传统预测模型对比,证明所提预测模型的预测精度和泛化能力更佳。Shi等[14]提出一种基于贝叶斯神经网络的热误差预测模型,与BP神经网络和多元线性回归相比,具有更高的预测精度,且能够保证不同工况下的优异预测性能。
然而,上述研究对于机床热误差补偿都是采用各种优化算法,其重点在于算法的改变。例如多元线性回归算法、岭回归算法、支持向量机、神经网络算法,都是在寻求模型优化的最佳方式。但模型的预测精度很大程度上还取决于所测数据中包含的信息。其中,时间参数均被忽略,导致目前研究成果存在了缺陷。文中将隐性参数——时间显性化,进一步明晰温度变量、时间变量与热误差之间的关系,提升热误差模型的预测精度和稳健性,同时降低温度敏感点的选择难度。
综上所述,选用常规的三轴数控加工中心为研究对象,采用国际标准“五点测量法”测量机床热误差,使用提出的融合时间的单温度敏感点建模方法( time-integrated approach to modeling thermal errors in machine tools with a single temperature-sensitive point,TSP)与传统的多温度敏感点多元回归建模方法(traditional multiple regression modeling methods for multiple temperature-sensitive points,TMP)进行比对分析。结果表明,所提出的TSP方法提升了模型的预测精度和稳健性。
1 热误差建模算法
传统的温度敏感点选择通常使用模糊聚类算法和灰色关联度算法[15-16],本文中使用该方法为传统建模方法筛选温度敏感点。建模算法选择多元回归方法,方便对比分析模型效果。
1.1 温度敏感点选择
1.1.1模糊聚类算法
模糊聚类算法可将相似的温度敏感点分为一类。通过各变量间的相关系数计算模糊相似矩阵R=[rij]n×n,相关系数由式(1)计算。
(1)
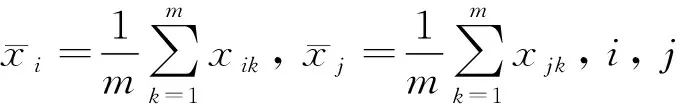
通过传递闭包将模糊矩阵转化为等价矩阵,完成模糊分类。
1.1.2灰色关联度算法
灰色关联度算法通过分析数据序列之间的几何相似程度来衡量数据序列之间的关联程度。灰色关联度计算值与相关序列之间的关联程度正相关。计算式为
(2)
(3)
式中:y为机床热误差数据;xi表示第i个温度测量点的所测值,i=1、2、…、m,m为温度测点数;y(k)为实测热误差数据的第k个测量值;xi(k)为第i温度测点的第k个测量值;γ(y,xi)为通过灰色关联分析出的热变形量与第温度测点之间的关联程度,ρ为分辨系数;Δy(k),xi(k)=|y(k)-xi(k)|为机床热误差与第i个温度测点数据之间的绝对差值,得到矩阵(Δy(k),x1(k)…Δy(k),xi(k)…Δy(k),xm(k)),Δmin和Δmax为矩阵中的最小值和最大值。
1.2 多元回归算法
在热误差建模中,多元线性回归算法可用来建立多个温度测点与热误差之间的联系,其表达式为
(4)
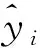
2 实验研究
2.1 实验装置
以三轴数控加工中心Vcenter-55为实验对象。为获取机床热误差数据,参考最新的国际标准IS0 230-3∶2020IDT,采用“五点测量法”进行测量。实验现场布置的 Vcenter-55机床实物如图1所示。
热误差的测量装置见图2。使用电涡流位移传感器采集热误差数据,传感器测量精度为1 μm。位移传感器通过夹具固定在机床工作台上,在X轴与Y轴方向上各安装2个位移传感器,Z轴方向上安装1个位移传感器,各位移传感器通过测量检验棒各方向的位移获得机床热误差。
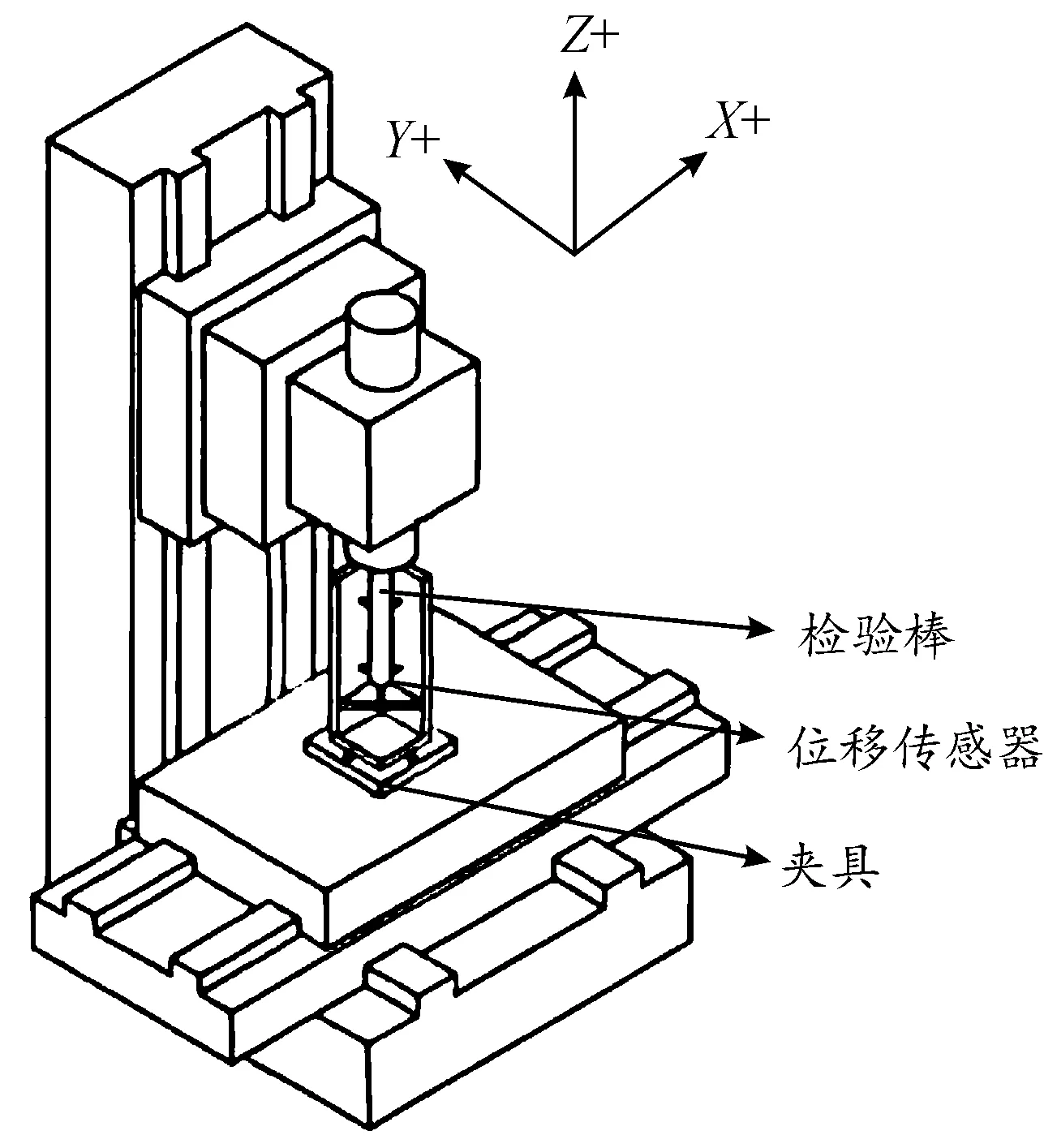
图2 热误差测量装置
数控机床的温度采集使用传感器DS18B20,将传感器安置在机床主要热源附近可测得温度数据。温度传感器测量范围是-55~125 ℃,最高分辨率为0.062 5 ℃,测量精度为±0.2 ℃。实验中使用10个温度传感器测量机床各热源的温度,传感器编号用T1—T10表示,具体安装位置见图3,传感器安放位置见表1。
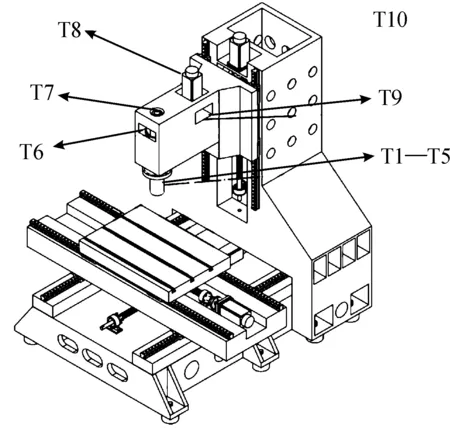
图3 温度传感器的安装位置

表1 传感器安放位置
2.2 实验安排
进行半年时间的实验测量,获得6批次不同环境温度下的热误差测量数据,分别记为K1—K6。主轴转速为2 500 r/min,直线进给为1 000 mm/min。进行圆周运动,每次运作时间为5 min,实验循环进行,总持续时间大于6 h。各批次实验的初始环境温度如表2所示。
2.3 实验数据分析
为方便分析温度数据,使用数据的相对值将各批次的温度数据分别绘制成折线图,K1和K6批次的温度数据如图4、图5所示。可以发现,不同环境温度下的各批次温度敏感点之间的变化趋势不同,增加了温度敏感点的选取难度。
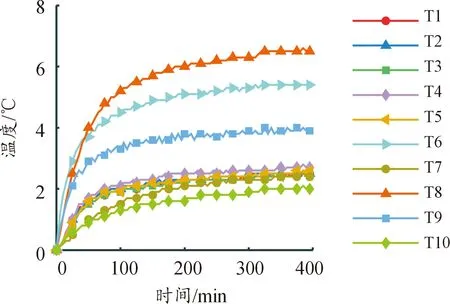
图5 K6批次温度数据曲线
根据实验结果,绘制各批次的Y、Z向热误差变化趋势曲线如图6、图7所示。由于X向热误差较小,可以忽略。故文中重点分析Y和Z向热误差规律。观察图6、图7发现,数控机床Y轴、Z轴的不同批次热误差随着时间的变化规律不同,说明预测模型需要准确描述不同环境温度下随着时间变化的热误差,这样才能使热误差模型更好地贴合实际热误差变化规律,提高模型的预测精度和稳健性。
由实验结果可知,对于热误差模型,时间是一个重要参数,因此提出了融合时间的单温度敏感点方法,相比于传统建模方法将时间影响参数给予显性化。为进一步分析时间参数显性化对模型预测效果的影响,将传统的“2个温度敏感点的建模方法”与提出的“融合时间的单温度敏感点建模方法(TSP)”进行机床热特性的预测效果比对分析,以验证时间参数显性化的优势。
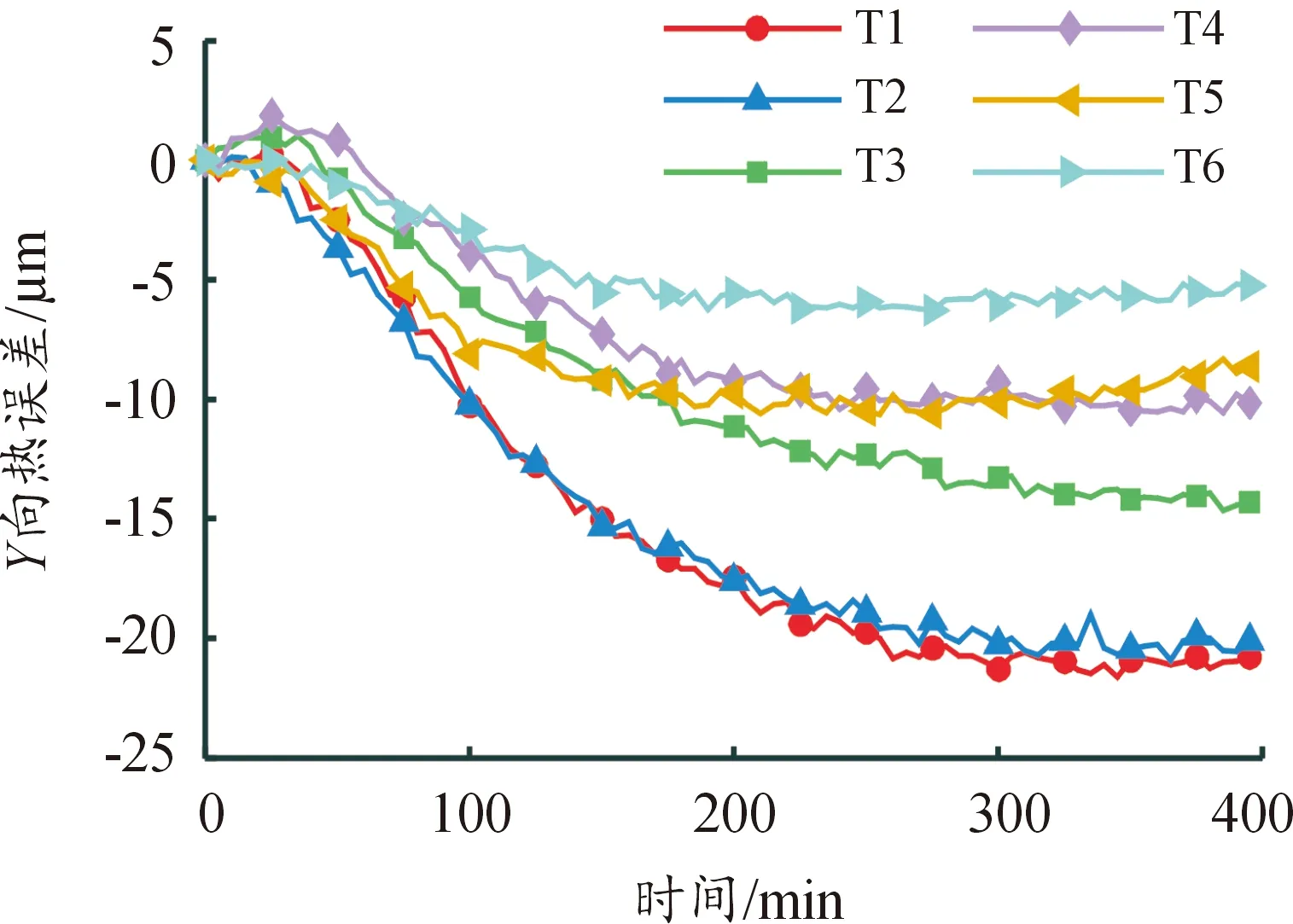
图6 K1—K6批次Y轴热误差数据曲线
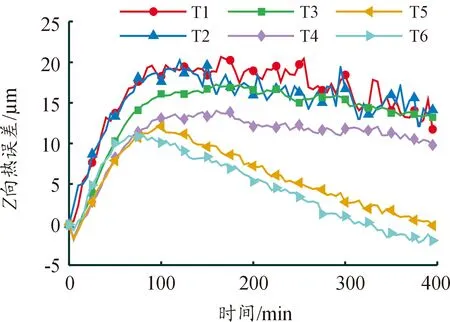
图7 K1—K6批次Z轴热误差数据曲线
3 传统热误差模型
传统热误差建模常以热误差值为因变量、以选择的温度敏感点为自变量建立多元回归模型。本节以主轴Y向热误差为例进行建模。
3.1 温度敏感点的选择
为建立数控机床的传统热误差模型(TMP),采用模糊聚类结合灰色关联度算法对K1—K6共6批次实验数据挑选温度敏感点,如表3所示。参与建模的为2个温度敏感点。

表3 各实验批次温度敏感点选择结果
3.2 主轴Y向传统热误差模型的建立
以K1批次数据建立模型为例。使用K1批次选择的温度敏感点,模型为
Y= 4.008 9-2.952 0T3-2.625 9T10
(5)
式中:T3自变量为温度敏感点T3的温度,T10自变量为温度敏感点T10的温度;4.008 9为模型的常数项,-2.952 0为温度变量T3的系数,-2.625 9为温度变量T10的系数。
通过表3中选择的对应实验批次的温度敏感点,建立Y向热误差各批次的多元回归模型,有关模型系数见表4。
表4中的d0为模型的常数项,d1为第一个温度敏感点的温度系数,d2为第二个温度敏感点的温度系数。

表4 各批次Y向热误差的多温度敏感点模型系数
4 TSP热误差模型
同样以主轴Y向热误差为例,采用TSP方法建模。所提出的TSP热误差模型以热误差值为因变量,以选择的单一温度敏感点和时间为自变量,建立多元回归模型。
4.1 温度敏感点的选择
TSP建模方法大幅降低了对温度敏感点选择的要求。根据温度敏感点与热误差之间的物理相关性,直接选择主轴上的某一个温度传感器作为温度敏感点,相较于传统的TMP建模方法,TSP对于温度敏感点的选择更加简单。例如,选择T1作为温度敏感点参与建模。
类冰川地质遗迹分布于黑龙江省中部的广阔区域,地理坐标为东经126°30′~130°30′,北纬45°40′~48°30′之间,目前包括黑龙江省铁力市朗乡花岗岩石林地质公园、宾县二龙·长寿山地质公园、集贤县七星峰地质公园和伊春市汤旺河小兴安岭石林国家地质公园、黑龙江凤凰山国家地质公园。其分布之广、种类之齐全、数量之多、特征之明显和保存之完好,在国内亦属少见(表1)。
4.2 TSP模型的建立
将选择的T1温度敏感点的温度值与对应时间t作为2个自变量,采用同样的多元回归算法参与建模。以使用K1批次数据建立模型为例,模型为
Y= 4.218 3-3.448 9T1-0.008 9t
(6)
式中:T1自变量为温度敏感点T1的温度;t自变量为时间;4.2183为模型的常数项,-3.448 9为T1的温度系数,-0.008 9为t的时间系数。各批次建立的回归模型系数见表5。表5中,c0为模型的常数项,c1为所选温度敏感点的温度系数,c2为时间系数。

表5 各批次Y向热误差使用T1的TSP模型系数
为分析主轴上不同温度敏感点采用TSP建模方法产生的热误差预测效果,将主轴上的1—5号温度传感器分别作为单温度敏感点参与TSP建模,对其预测效果进行比对分析。
4.3 TSP建模方法中主轴温度敏感点选择不同的影响分析
基于以上单温度敏感点的建模过程,研究主轴上不同温度敏感点对模型的预测效果。
使用模型预测值的残余标准差来衡量建模精度。残余标准差S的计算式为
(7)
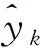
使用预测残余标准差的平均值Smean评定模型对所有批次数据的预测精度。
(8)
使用标准差Sstd来计算模型对所有数据的稳健性。
(9)
式中:Si为模型对第i批次数据的预测残余标准差;Smean为预测残余标准差的平均值。
根据数控机床热误差与温度的物理相关性,分别选择主轴上的1—5号中的一个温度敏感点,并使用各批次数据建立热误差模型对其他批次数据进行预测。将预测精度与稳健性绘制成曲线,见图8。
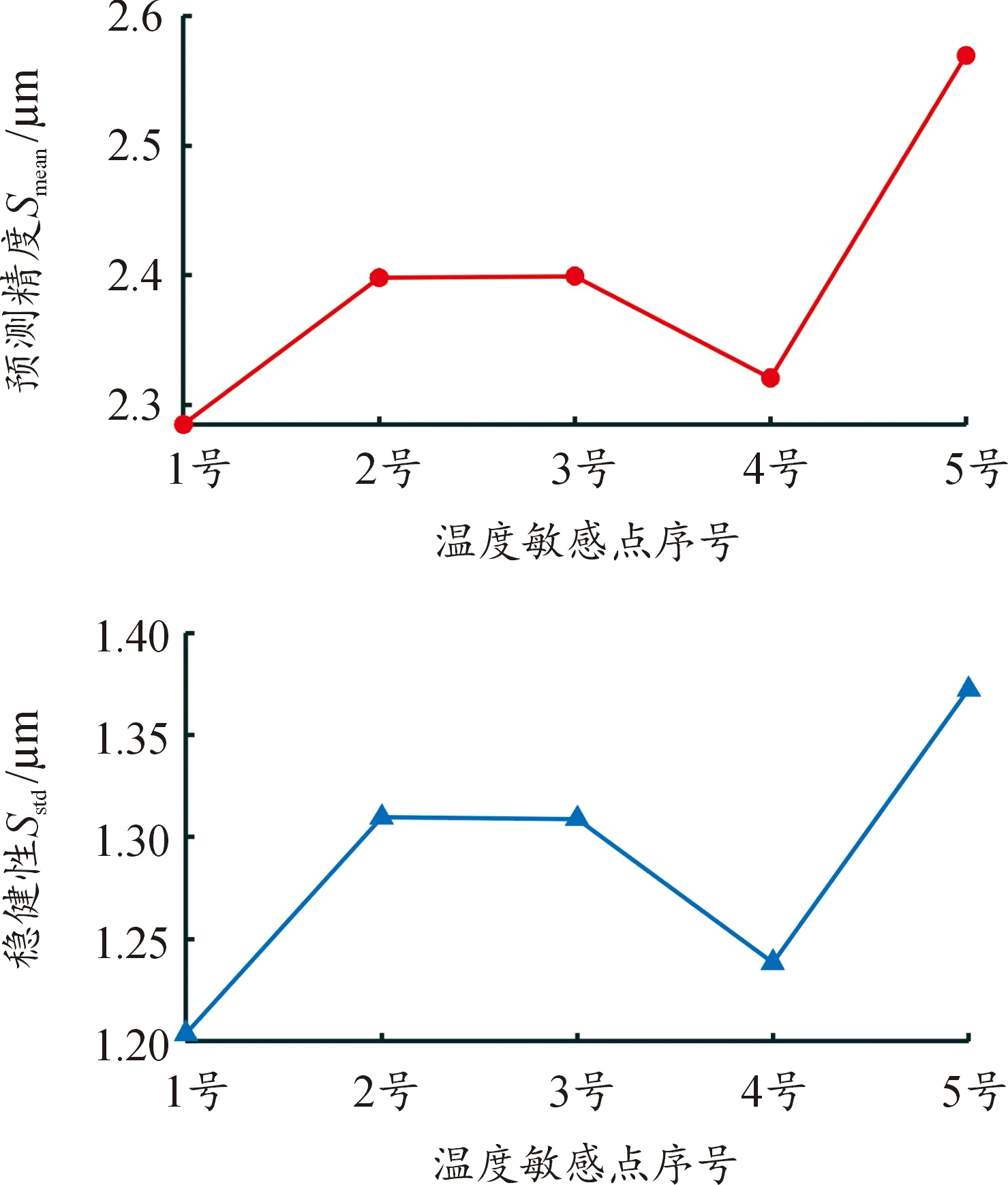
图8 主轴上各温度敏感点对模型预测效果的影响
从图8中可以看出,采用TSP建模方法,选择1—5号温度传感器作为敏感点参与建模,预测精度及稳健性均较高,在2.57 μm以内。其中,选择1号温度敏感点时,模型的预测精度和稳健性最高,分别达到2.28 μm和1.20 μm。选择5号温度敏感点时,模型的预测精度和稳健性最差,分别为2.57、1.37 μm。
为说明TSP方法对温度敏感点选择的良好包容性,使用主轴上效果最差的5号温度敏感点建立热误差模型,与传统的TMP方法的预测效果进行比对分析。
采用TSP建模方法对Y向热误差建模的具体模型如表6所示。
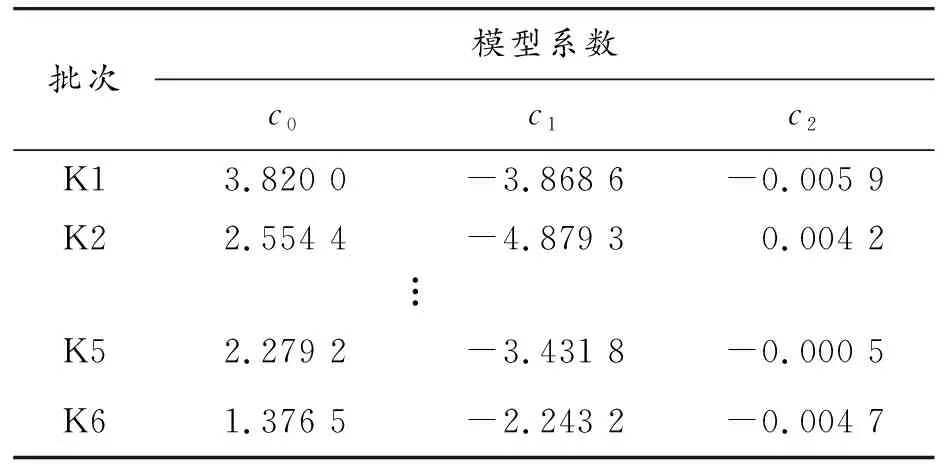
表6 各批次Y向热误差使用T5的TSP模型
5 模型精度分析
为验证提出的融合时间的单温度敏感点方法的有效性和温度敏感点选择的包容性,对传统的TMP建模方法与提出的TSP建模方法进行对比分析。
根据TMP方法所建立的K1—K6批次Y向传统热误差模型(记为M1—M6),通过式(7),分别对K1—K6批次数据进行预测及拟合精度分析。TMP的Y向热误差预测结果见图9,TMP与TSP的Y向热误差建模效果见表7。

图9 TMP的Y向热误差预测结果
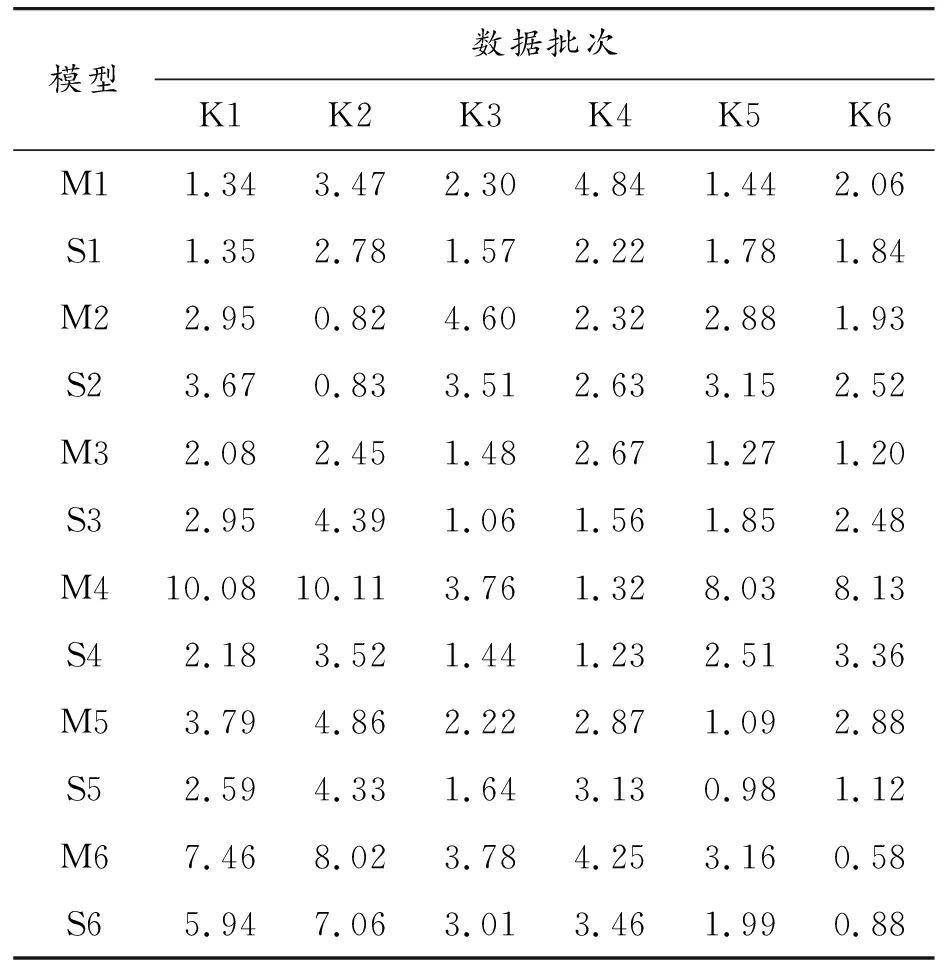
表7 TMP与TSP的Y向热误差建模效果 μm
根据所建立的K1—K6批次Y向TSP模型(记为S1—S6),通过式(7),分别对K1—K6批次数据进行预测及拟合精度分析。TSP的Y向热误差预测结果见图10。
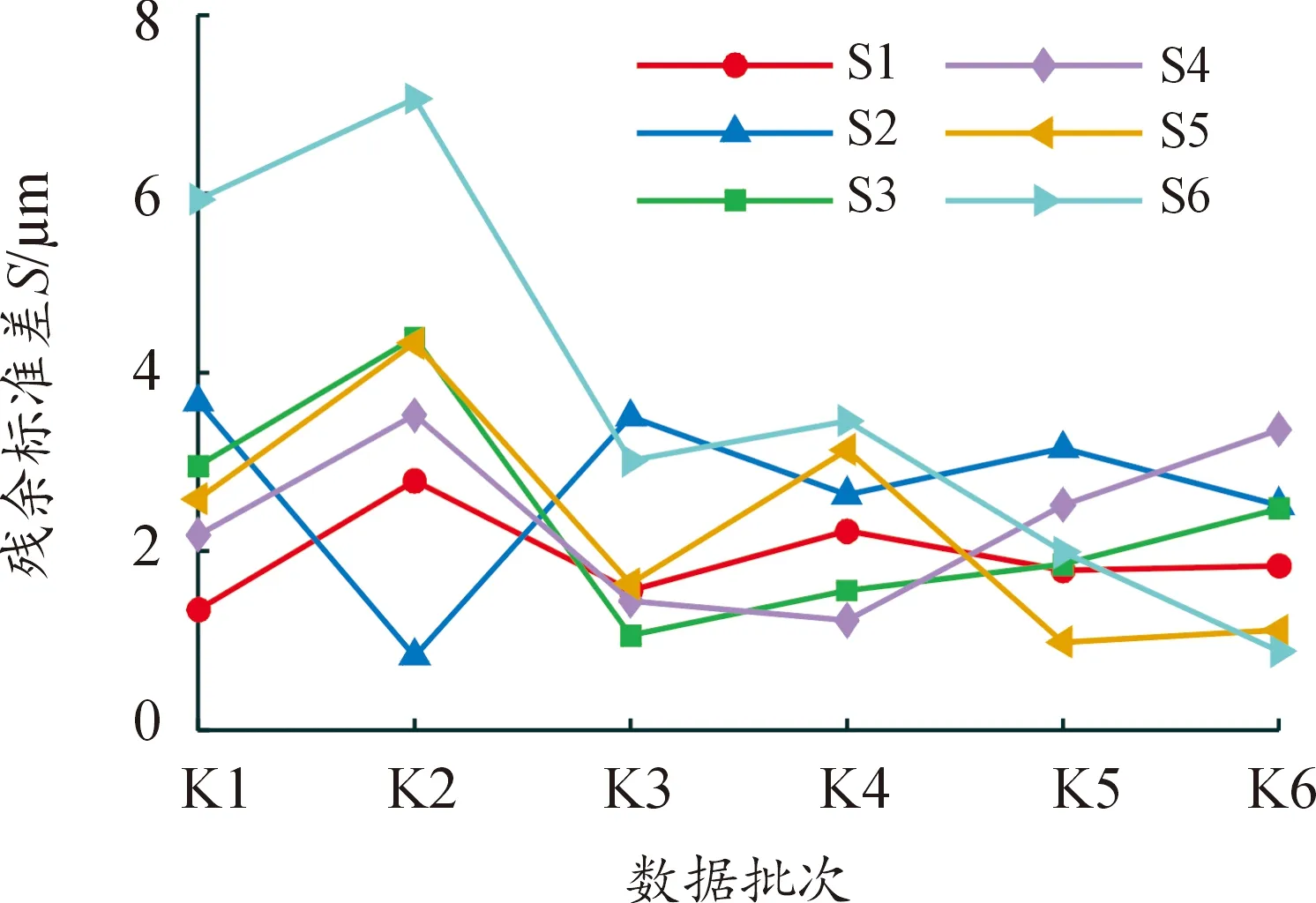
图10 TSP的Y向热误差预测结果
Y向热误差不同模型的建模效果见表8。相比较TMP方法,通过式(8)和式(9)计算得到TSP方法对所有批次数据的预测精度和稳健性分别提升了28.0%和47.1%。

表8 Y向热误差不同模型的建模效果 μm
同理,对主轴Z向热误差进行2种建模方法效果比对,结果如表9所示。相比较TMP方法,TSP方法的预测精度和稳健性分别提升了45.1%和57.7%。
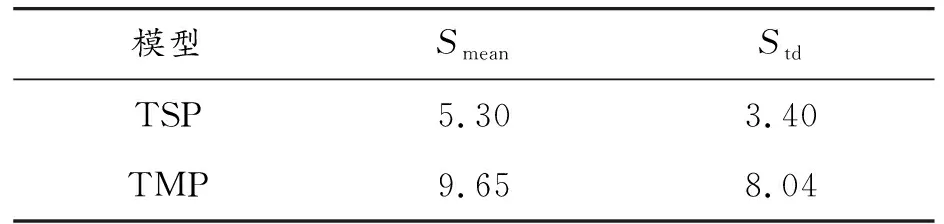
表9 Z向不同模型的建模效果 μm
结合数控机床Y向热误差与Z向热误差的建模效果对比,所提出的TSP建模方法效果相比TMP方法得到了较大提升。这说明时间参数的引入能够提高模型的预测精度和稳健性,且能够降低温度敏感点选择的难度。
6 结论
1) TSP方法对半年的Y向热误差实验数据预测精度达到2.57 μm,稳健性达到1.37 μm。相较于传统的热误差建模TMP方法,TSP方法使模型的预测精度和稳健性分别提升了28.0%和47.1%。
2) TSP方法对半年的Z向热误差实验数据预测精度达到5.30 μm,稳健性达到3.40 μm。相较于传统的热误差建模TMP方法,TSP方法使得模型的预测精度和稳健性分别提升了45.0%和57.7%。
3) TSP方法在降低温度敏感点选择难度的情况下,热误差模型更加接近机床在不同环境温度下热误差的真实变化规律,提升了模型预测的精度和稳健性。
4) TSP方法主要使用多元回归算法,在数控机床热误差建模中,时间参数在不同算法中融合的效果还有待进一步研究。
