调和犹豫模糊偏好关系及其在群决策中的应用
2023-12-12耿生玲
冯 雪,耿生玲
(1.青海民族大学 数学与统计学院, 西宁 810007; 2.青海师范大学 计算机学院, 西宁 810016;3.藏语智能信息处理及应用国家重点实验室, 西宁 810008)
0 引言
最早由Saaty[1]教授创立的层次分析法(analytic hierarchy process,AHP)被应用到经济学、心理学、计算机科学以及医学等领域。但随着数字经济快速发展,由于人类思维的模糊性和决策问题的复杂性,在实际决策中存在许多不确定性,Zadeh[2]提出了模糊集的概念,随后将模糊集理论引入到偏好关系中,Orlovsky[3]提出了模糊偏好关系。但随着决策问题的不断复杂化,决策者在决策过程中表现出一定的犹豫性,Xia等[4]给出了犹豫模糊偏好关系的定义,用犹豫模糊元表示评价对象之间的优劣程度,从而体现决策者的犹豫性。随着科学研究的不断深入和发展,犹豫模糊集应用于决策问题的缺陷也显现出来,例如,当决策过程中具有不同的评估意见时,直接用犹豫模糊集去处理显得过于简单,未考虑不同评估值的权重问题。经过不断的深入研究,学者们希望通过某种形式能够更加准确地描述决策过程中的不确定信息,Xu等[5]、Gao等[6]提出了概率犹豫模糊集的概念,在犹豫模糊元的基础上添加了对应隶属度的权重信息(即概率),构建了概率犹豫模糊元,从而定义了概率犹豫模糊集,能够更加细致地表达出决策过程中的不确定信息。然而,随着实际应用的需要而不断拓展其应用范围,以及学者们研究的持续深入,我们发现犹豫模糊元和概率犹豫模糊元存在着计算繁琐、计算量不可控、与数量运算规则不相容等问题。朱峰等[7]首先提出了调和概率犹豫模糊元的概念,同时定义了交叉熵测度,可用于测量概率犹豫模糊元之间的差异程度。胡悦等[8]、Wu等[9]在概率语言术语集的基础上,给出了相关的简化运算规则,可将概率语言术语集的不同概率分布调整为相同概率分布。Lin等[10]给出了完整的概率分裂算法,解决了概率犹豫模糊集运算中的一个主要问题,通过概率分裂算法可将一组概率分布不同的概率犹豫模糊元调整为概率分布相同的概率犹豫模糊元。方冰等[11]基于以上研究,给出了调和犹豫模糊信息的运算法则、聚合算子、距离公式和混合熵测度,同时建立了调和犹豫模糊环境下的决策理论。近几年,基于模糊偏好关系的决策问题研究得到了显著的发展[12-14]。
群体决策可以充分利用每个人的知识、经验和能力,有效地将团队成员的资源进行整合,从而达到更好的决策结果; 可以将多个人的视角、经验和信息进行整合,使得决策所依据的信息更加全面,决策结果更加准确; 可以避免个体决策中可能存在的偏见和盲点,从而提高决策的质量和准确性; 可以考虑多方利益,从而达到更加平衡的决策结果,使得各方都能够得到满意的结果。根据实际应用的需要,模糊偏好关系理论已经涉及各类决策问题[15-19]。而在偏好关系中,一个重要的研究问题就是一致性[20-26],可用其判断专家所给出偏好信息的合理性。内在逻辑合理的偏好关系满足一致性,所做出的决策结果也是正确合理的。但是,在实际案例中,很难得到完全一致的偏好关系。为了解决此类问题,需要对偏好关系的不一致性程度进行量化,从而在保证尽可能多的偏好信息不变动的情况下,将不一致元素进行调整,得到一个新的偏好关系,使其满足所定义的一致性。
调和犹豫模糊偏好关系编程简单、易于实现、计算量小且运算相容,大大简化了具体应用中的操作过程。本文中给出了调和犹豫模糊偏好关系和乘性一致的调和犹豫模糊偏好关系的定义,并通过调整算法研究了调和犹豫模糊偏好关系的一致性,此算法可用于检测和提高一致性水平。最后,构建基于调和犹豫模糊偏好关系的群决策方法,并将其应用于紧急预案如火灾现场救援决策选择问题。
1 预备知识
1.1 相关模糊集定义及其运算
定义1[4,27]设非空有限论域V,则V上的犹豫模糊集定义为A={〈x,hA(x)〉|x∈X},其中hA(x)表示x属于A的可能隶属度,且是[0,1]中的一些数值,并称hA(x)=h(x)为犹豫模糊元。论域V上的所有犹豫模糊集记为HF(V)。
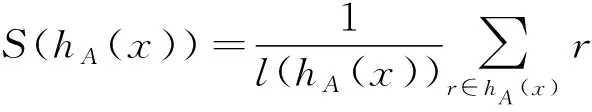
定义3[29]给定犹豫模糊元h(x),其偏差度为:

比较2个犹豫模糊元的大小,Liao等[20]给出如下法则:
1) 如果S(h1)>S(h2),则h1>h2;

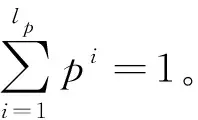
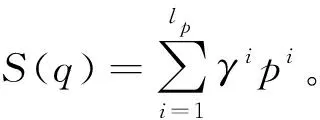
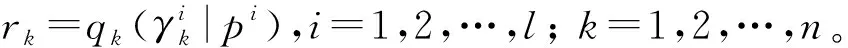
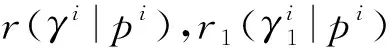
1.2 模糊偏好关系
定义8[17]给定备选项集X={X1,X2,…,Xn},定义在X上的模糊偏好关系如下:
式中:pij表示Xi对Xj的偏好程度,pij∈[0,1]且pii=0.5,pij+pji=1。pij=0.5表示Xi与Xj无差别;pij=1表示Xi完全优于Xj;pij>0.5表示Xi优于Xj,1≤i,j≤n。


对所有i,j=1,2,…,n,i≠j。其中,mij表示hij中元素的个数。

2 调和犹豫模糊偏好关系及其乘性一致性判定
本节中,将定义调和犹豫模糊偏好关系和乘性一致的调和犹豫模糊偏好关系,并给出一致性判定定理。
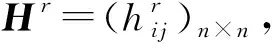
(1)

注1调和犹豫模糊偏好关系中,调和犹豫模糊元是一组基数相同的概率犹豫模糊元,同时也具有相同的概率分布。
注2通过对一组犹豫模糊元、概率犹豫模糊元进行概率调整,可以得到调和犹豫模糊元。
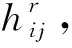
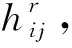
例1假设HP为概率犹豫模糊偏好关系。
通过概率分裂算法,可以将其中的概率犹豫模糊元调整为调和犹豫模糊元,得到调和犹豫模糊偏好关系,如下所示:
例2假设H为概率犹豫模糊偏好关系。
可先将H调整为等概率的概率犹豫模糊偏好关系,再通过概率分裂算法,调整为调和犹豫模糊偏好关系。
注5由定义5可知,通过概率分裂算法调整后,对得分值和偏差度没有影响。因此,调整后的调和犹豫模糊元能够保持原本的序关系。
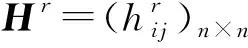
pij·pjk·pki=pik·pkj·pji,i,j,k∈N
(2)
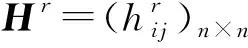
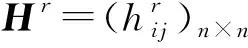
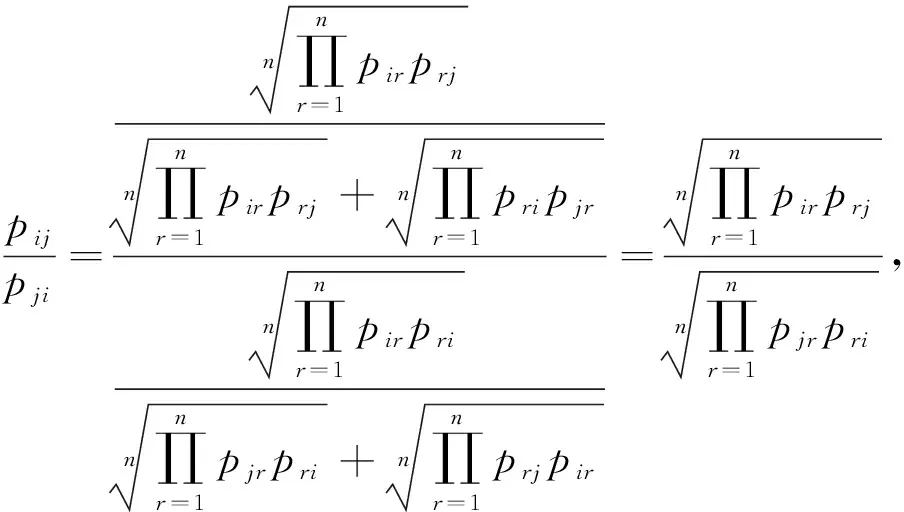
由定理1可知,当P=(pij)n×n满足一定条件时,可以用其判断Hr是否乘性一致。
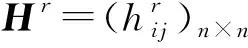
(3)
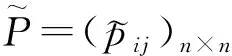
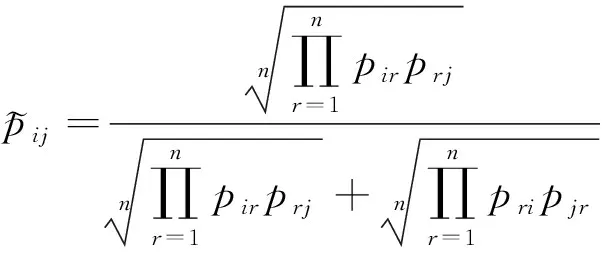
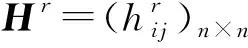
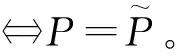
3 调和犹豫模糊偏好关系的乘性一致性水平及调整算法
基于模糊偏好关系的决策问题研究,必须考虑偏好关系一致性,因为偏好关系的不一致会影响决策结果的科学性。然而,在实际问题中,很难得到一致的偏好关系。我们常常会对所给偏好关系的不一致性程度进行量化,从而在保证尽可能多的偏好信息不变动的情况下,将不一致元素进行调整,得到一个新的偏好关系,使其满足所定义的一致性。
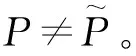
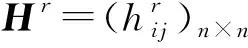
(4)
注6当WCI(Hr)=0时,调和犹豫模糊偏好关系Hr一定是乘性一致的。
大量实验证明,WCI(Hr)=0很难达到。为了解决此问题,在实际问题中,可以通过给定可接受乘性一致的阈值来确保Hr的乘性一致性。
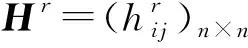
算法1调和犹豫模糊偏好关系可接受一致性调整算法

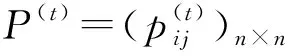
步骤3计算WCI(Hr),若WCI(Hr)≤δ0,转至步骤5; 否则进入下一步。
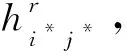
(5)
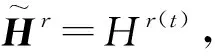
步骤6结束。
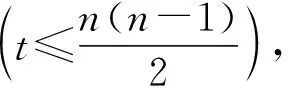
注8在算法1中,对于不满足可接受乘性一致性的调和犹豫模糊偏好关系,步骤 4中仅对不一致性程度最高的元素进行调整,并非是全部元素,这样大大降低了计算量,并且最大程度保留了原始信息。
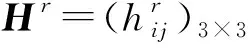
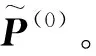
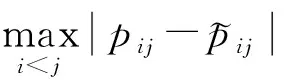
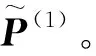
计算可得WCI(Hr(1))=0.020 3<δ0,所以Hr(1)是可接受乘性一致的调和犹豫模糊偏好关系。
针对犹豫模糊信息和概率犹豫模糊信息在群决策问题研究中出现的不足,在前文中,考虑将犹豫模糊信息和概率犹豫模糊信息纳入统一处理框架,定义了调和犹豫模糊偏好关系。我们发现,调和犹豫模糊偏好关系能够全面体现专家所给出的偏好信息,并且可以表达出偏好信息的重要程度,还具有偏好结构统一规律等特点,更适合应用于群体决策问题。基于此,我们将研究基于调和犹豫模糊偏好关系的群决策方法。
4 调和犹豫模糊偏好关系在群决策中的应用
基于调和犹豫模糊偏好关系的群决策方法能够更好地体现专家的偏好信息,并且考虑了偏好信息的乘性一致性水平要求,提高了群体决策的准确性和可靠性,为解决群体决策中存在的问题提供了新的思路和方法。本节中,将给出基于调和犹豫模糊偏好关系的群决策方法。
算法2调和犹豫模糊偏好关系的群决策算法
输入 偏好关系H、HP、Hr,备选项集X={X1,X2,…,Xn},一致性阈值δ0。
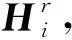

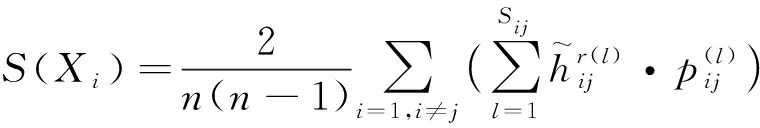
步骤4输出Xi的排序,选择最优选项。
步骤5结束。
例4消防救援常常面对时间紧急、情况危急、信息缺乏的状况。为了提高火灾现场救援效率,根据相关专家的理论知识及指挥官的实践经验,考虑到火灾警报、启动救援程序、快速出警、现场救援等方面的因素,给出4个消防救援应急方案A={A1,A2,A3,A4},现邀请4名决策专家根据各自擅长的方式,给出以下偏好关系。
将各专家所给出的偏好关系调整为调和犹豫模糊偏好关系。
写出综合调和犹豫模糊偏好关系Hr:
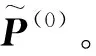
设δ0=0.025,计算可得WCI(Hr(0))=0.045 1,则WCI(Hr(0))>δ0。通过2次调整,构建新的调和犹豫模糊偏好关系。
Hr(2)=
计算可得WCI(Hr(2))=0.022 9<δ0,则Hr(2)是可接受乘性一致的。
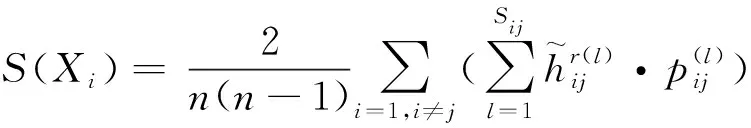
5 结论
基于调和犹豫模糊元克服了已有模糊理论的缺陷,其编程简单、易于实现、计算量小且运算相容,大大简化了具体应用中的操作过程。给出了调和犹豫模糊偏好关系和乘性一致的调和犹豫模糊偏好关系的定义,通过调整算法研究了调和犹豫模糊偏好关系的一致性,此算法可用于检测和提高一致性水平。最后,构建基于调和犹豫模糊偏好关系的群决策方法,将其应用于紧急预案,如火灾现场救援决策选择问题。在后续的研究工作中,我们将继续深入研究其一致性问题,尽量做到原始偏好信息少变的前提下,满足相应的一致性。
