压缩感知电流互感器传变特性辨识方法

2023-12-11王学伟任红宇袁瑞铭李文文王国兴

北京化工大学学报（自然科学版） 2023年6期

王学伟任红宇袁瑞铭李文文王国兴

(1.北京化工大学信息科学与技术学院, 北京 100029;2.国网冀北电力有限公司计量中心, 北京 100045)

引言

在“碳达峰”和“碳中和”以及新型电力系统建设的大背景下,我国能源需求不断增加。随着轧钢、电弧炼钢等非线性负荷的大量应用[1],负荷的电流呈现出复杂宽频带谐波扰动的特点。电流互感器作为负荷电流变换采集的设备,其传变特性是影响电能计量综合误差的主要因素。因此,围绕电流互感器宽频带传变特性的快速准确辨识方法进行研究,对于提高电能计量的准确性具有重要意义。

目前,研究者提出电流互感器(CT)传变特性的系统辨识方法,主要采用一次侧频域信号扫频的方法辨识CT 传变特性,如新型差动电流互感器[2]、罗氏线圈电流互感器[3]以及光电式电流互感器[4]等的辨识,或者采用一次侧频域谐波信号扫频的方法辨识CT 传变特性,如电磁式电流互感器的辨识[5]。目前,CT 传变特性的扫频系统辨识方法应用广泛、精度高,但在多点扫频频率下采样一次与二次侧电流再计算得到CT 的传变特性,需要耗费大量的时间。 CT 扫频系统辨识方法效率低的问题尚未解决,并且始终缺乏高效的辨识方法,如何产生合适的辨识激励信号,高效辨识CT 的传变特性,还有待在理论方面获得突破。

压缩感知作为近年来出现的高效的信号处理方法[6],广泛应用于信号和图像处理以及系统辨识领域[7]。目前压缩感知辨识理论主要应用于特定模型参数的辨识,如线性参变(linear parametric variation, LPV)模型[8]、Hammerstein 时间模型[9]、网络拓扑结构的辨识[10]、叶尖定时信号[11]和智能电网中谐波源[12]的辨识等,但尚未有针对CT 传变特性的压缩感知系统辨识方法。在压缩感知理论中,精确重构的先验条件为信号是稀疏的或可稀疏化的,因此,如何设计并构造稀疏字典,满足CT 传变特性的稀疏先验条件,是CT 传变特性压缩感知系统辨识中需要解决的问题。

为解决CT 传变特性时频域的快速准确系统辨识的理论问题,本文首先推导了CT 的Jiles-Atherton (J-A)模型传递函数,其次提出了CT 压缩感知系统辨识架构,构造了CT 系统传变函数的多频正弦信号稀疏字典以产生压缩感知辨识激励信号,随后构建了Toeplitz 降维测量矩阵,通过压缩采样匹配追踪算法辨识CT 传变特性。最后通过仿真实验对压缩感知系统辨识方法的性能进行了验证。

1 J-A 模型电流互感器传递函数的推导

传统CT 主要基于电磁感应原理[13],CT 等效电路模型如图1 所示。其中i1为一次侧电流,i′1为二次侧电流,Le、Re为励磁阻抗,L2、R2为二次绕组阻抗,L3、R3为二次侧负载阻抗。根据图1 中的CT 等效电路,将电流互感器从N1、N2处分成一次侧、二次侧两部分,根据国家标准GB 1208—2006《电流互感器》,在CT 工作频率范围内,CT 二次侧负载等效为电阻,因此在后续的推导过程中将L3省略。同时,得到CT 频域等效电路如图2 所示。其中,L1、R1为一次侧绕组阻抗,C1、C2分别为初级、次级极间电容。在工频下,C1、C2的值一般较小[14]。

图1 电流互感器T 型等效电路Fig.1 T-type equivalent circuit of the current transformer

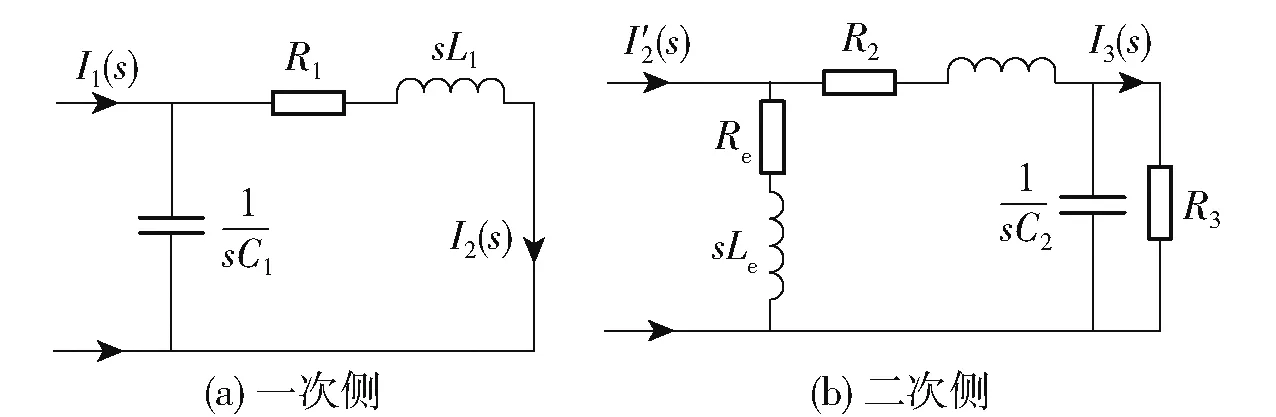
图2 电流互感器频域等效电路Fig.2 Frequency domain equivalent circuit of the current transformer

为了进一步推导CT 的传递函数,结合图2,分别从一次侧、二次侧频域部分进行传递函数的推导。根据图2(a)可以得到CT 一次侧传递函数为

式中,Z1为一次绕组阻抗且Z1=R1+sL1。当C1很小时,G1(s) =1,表示电流信号在一次侧幅值没有衰减,相位没有偏移。

在CT 为理想变量器条件下,根据CT 链式守恒原理N1×I1=N2×I2,一次侧、二次侧等效电路间的关系如式(2)所示。

式中,Re+R2≫R3,Re≫R2,Le≫L2,ω0=Re/Le,P=Le/R3C2(L2+Le),ω1= 1/R3C2,ω2= (R2+Re)/(L2+Le)。式(6)表明,传统电流互感器的传递函数为具有1 个单零点和两个极点的线性系统。

2 压缩感知重构

在压缩感知理论中,若信号x∈RN×1是稀疏的或者在某个变换域Ψ∈RN×N内具有稀疏性[15],则可以通过相应的随机观测矩阵进行压缩采样,得到一个含有原始信号相关信息且数据量远低于原始信号的压缩信号,再通过求解欠定方程组的问题进行重构[16]。压缩感知中的稀疏变换过程如式(7)所示。

式中,s∈RN×1为x在变换域Ψ中的稀疏信号。对于信号s,其压缩采样过程如式(8)所示。

式中,y∈RM×1(M≪N)为观测采样值,Φ为测量矩阵,θ为传感矩阵。根据式(8)可将压缩感知重构过程表示成如图3 所示。

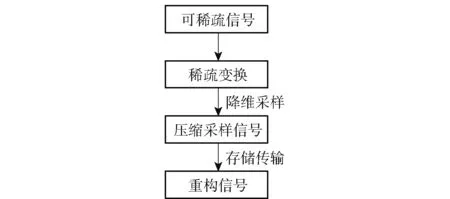
图3 压缩感知信号重构Fig.3 Compressed sensing signal reconstruction

同时相应的测量矩阵Φ需满足有限等距特性(restricted isometry property, RIP)[17]。对于K稀疏的信号s∈RN×1和常数δk∈(0,1),满足

在满足RIP 准则的基础上,压缩感知重构过程可转化为求解欠定方程组的问题,即求解最小l0范数的问题,结合式(8)可表示为

最终,通过采样信号y求出稀疏信号^s,再通过^x=Ψ-1^s求出最终的重构信号^x。

为进行CT 传变特性系统辨识,结合压缩感知理论,可将CT 看作一个参数客观存在的待辨识系统,而传感矩阵作为该系统的输入信号,由此提出CT 频域传变特性压缩感知系统辨识架构。

3 电流互感器频域传变特性的压缩感知辨识架构与辨识方法

3.1 构建电流互感器传变函数的稀疏字典

在CT 系统辨识过程中,由于无法直接采用压缩感知测量矩阵作为输入信号进行传变特性的辨识,故需要将系统的输入输出调整为电流信号。为解决CT 传变特性的系统辨识问题,提出压缩感知系统辨识架构,如图4 所示。

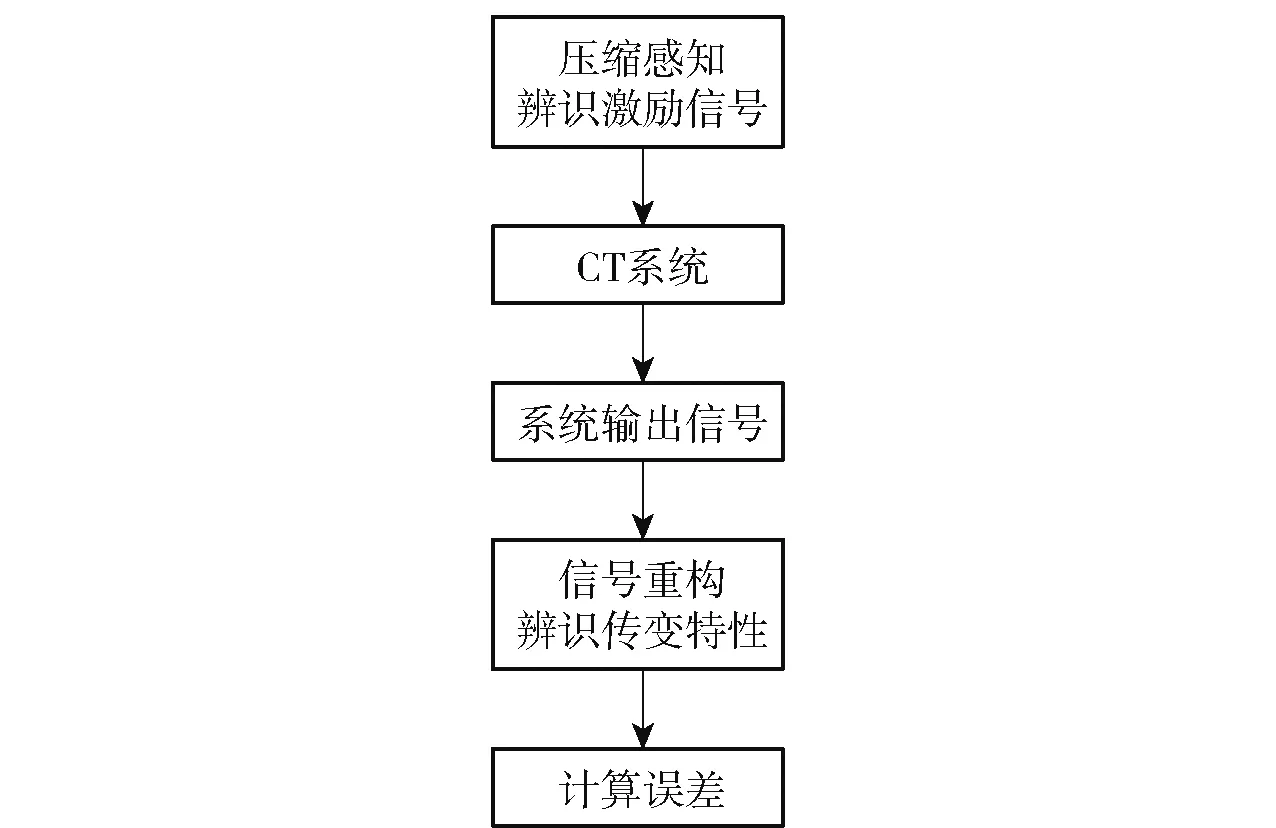
图4 CT 压缩感知系统辨识架构Fig.4 CT compressed sensing system identification architecture

根据图4,构造一种多频率正弦信号稀疏字典,产生压缩感知辨识信号,输入CT 系统,再根据系统输出信号,基于所提出的架构完成CT 系统传变特性的压缩感知辨识。

首先构造多频率正弦信号,设定长度为M点的截断离散单频正弦信号如式(11)所示。

式中,ω1=2π(f1/fs)表示初始角频率。

其次,采用N个M点截断离散单频正弦信号构建矩阵如式(13)所示。

式中,矩阵LM×N中第l列表示角频率为ωl的离散正弦信号。

然后,构建CT 的传变函数向量如式(14)所示。

式(14)表示待辨识的CT 系统。由式(13)、(14)可知所构建的矩阵LM×N包含了CT 系统的各个频率分量,可以保证系统解的稀疏性。因此,矩阵LM×N为CT 传变函数的稀疏字典,满足压缩感知稀疏条件。

3.2 电流互感器频域传变特性压缩感知辨识过程

为了实现电流互感器的精确辨识,同时降低压缩感知硬件的复杂度,根据图4,考虑实际部署的便捷性,采用Toeplitz 矩阵Φ作为测量矩阵,且当信号稀疏度K≤c1M3/ln (N/M)(N、M分别为测量矩阵的行、列数,c1为常数)时,Toeplitz 矩阵满足RIP 准则[18]。

根据式(13)、(14),CT 的压缩感知时频域系统输出信号为

根据式(15),可将CT 传变函数HN×1的辨识问题拟合为压缩感知重构问题,根据式(8),可将CT二次侧的输出信号进一步写为

Y′M×1=ΦM×MLM×NHN×1(16)

其中,ΦM×M为Toeplitz 测量矩阵。由于式(16)为一个NP 难题,无法直接求出稀疏向量HN×1的值,根据式(10),可将式(16)写为求解最小l0范数的问题

则可以通过求解式(17)非零元素的值,再根据构造的压缩感知稀疏字典矩阵LM×N确定HN×1中非零元素所对应的频率分量,进而拟合出CT 的传变函数和二次侧电流有效值。所采用的构造压缩感知矩阵来表示辨识激励信号的方法,有效地避免了常规压缩感知理论中使用压缩感知采样电路的难题。

3.3 电流互感器频域传变特性的压缩感知重构算法

本文主要使用压缩采样匹配追踪(CoSaMP)算法,该算法由Needell 等[19]提出,在正交匹配追踪算法基础上增加了原子选择后的回溯机制[20],整体重构快、精确度高。其核心步骤归纳如下。

(1)输入传感矩阵θ=ΦM×M LM×N,采样信号y(y=Y′M×1)以及稀疏度K;输出系数σK∈HN×1。

(2)初始化设定:t=1,残差ro=y,索引集Λ0=∅,候选原子集合ψ0=∅。

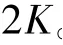
(6)更新残差并令t=t+1,如果t＞K或残差rk=0则停止,否则返回步骤(3)。

4 电流互感器频域传变特性压缩感知辨识性能分析

4.1 扫频仿真实验与结果分析

由式(6)可知,CT 为包含单零点和两个极点的线性系统。基于PSCAD 软件平台中电流互感器的J-A 模型,结合式(6)电流互感器的传递函数,根据电流互感器的实际参数情况,设定PSCAD 软件平台中电流互感器的额定参数,具体如表1 所示。建立J-A 模型电流互感器作为辨识用电流互感器。

表1 电流互感器额定参数Table 1 Rated parameters of the current transformer

扫频系统辨识过程主要通过调整CT 一次侧的电流信号频率依次得到不同频率下的二次侧电流信号,再通过Matlab 计算得到CT 的传变特性。 CT 的传变特性包括比差传变特性和角差传变特性,计算方法如下。

1)比差

式中,K为CT 一次侧和二次侧电流信号的额定变比;I1为CT 一次侧实际输入的电流;I2为对应测量得到的二次侧电流。

2)角差

式中,ϕ1为CT 一次侧实际输入的电流信号相位;ϕ2为对应测量得到的二次侧电流信号相位。

结合式(18)、(19),扫频系统辨识流程如图5所示。

图5 扫频系统辨识流程Fig.5 Identification process of the frequency sweep system

在仿真辨识中,保持CT 一次侧电流幅值I1n为100 A(I1n表示不同单一频率下的一次侧电流信号,n=1,2,…,N),根据图5,通过调整CT 一次侧电流频率(10 ～3 500 Hz),利用PSCAD 中的CT 系统得到二次侧电流,经Matlab 计算后,得到CT 的比差、角差传变特性如图6 所示。

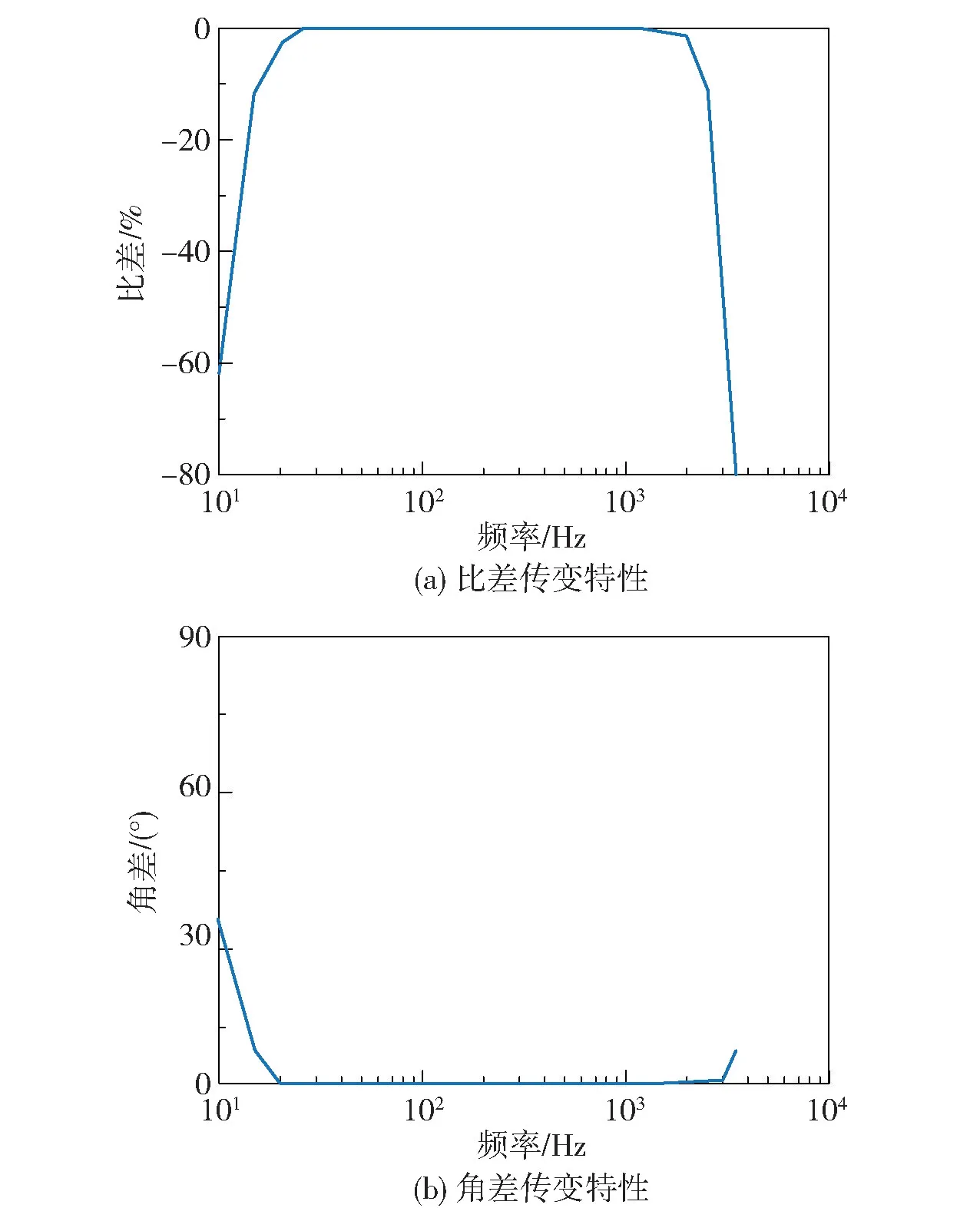
图6 单次频率法的CT 频率特性Fig.6 CT amplitude frequency characteristics of the single frequency method

从图6 可以看出,J-A 模型电流互感器的通带频率范围为25 ～2 500 Hz,低于或超出此频率范围,电流互感器将逐步产生大量误差。

4.2 压缩感知仿真实验与结果分析

为评价CT 传变特性压缩感知系统辨识的性能及准确度,引入以下3 个参数。

1)各频率分量下CT 频域传变特性重构后的相对误差,计算公式如式(20)所示。

式中,J表示原系统参数,J*表示辨识得到的系统参数。

2)为评价CT 压缩感知系统辨识方法的准确度,采用压缩感知评价方法,计算CT 压缩感知系统辨识方法与扫频系统辨识方法二次侧输出电流有效值间的均方误差,计算公式如式(21)所示。

式中,^I2n表示不同频率分量下CT 压缩感知辨识方法二次侧输出电流信号的有效值,N表示频率分量数。由于CT 的系统辨识不涉及压缩系数和信噪比,因此本文不使用其作为评判指标。

3)CT 压缩感知系统辨识方法和扫频系统辨识方法所需时间对比。

压缩采样匹配追踪(CoSaMP)算法下CT 传变特性的系统辨识结果如图7 所示。

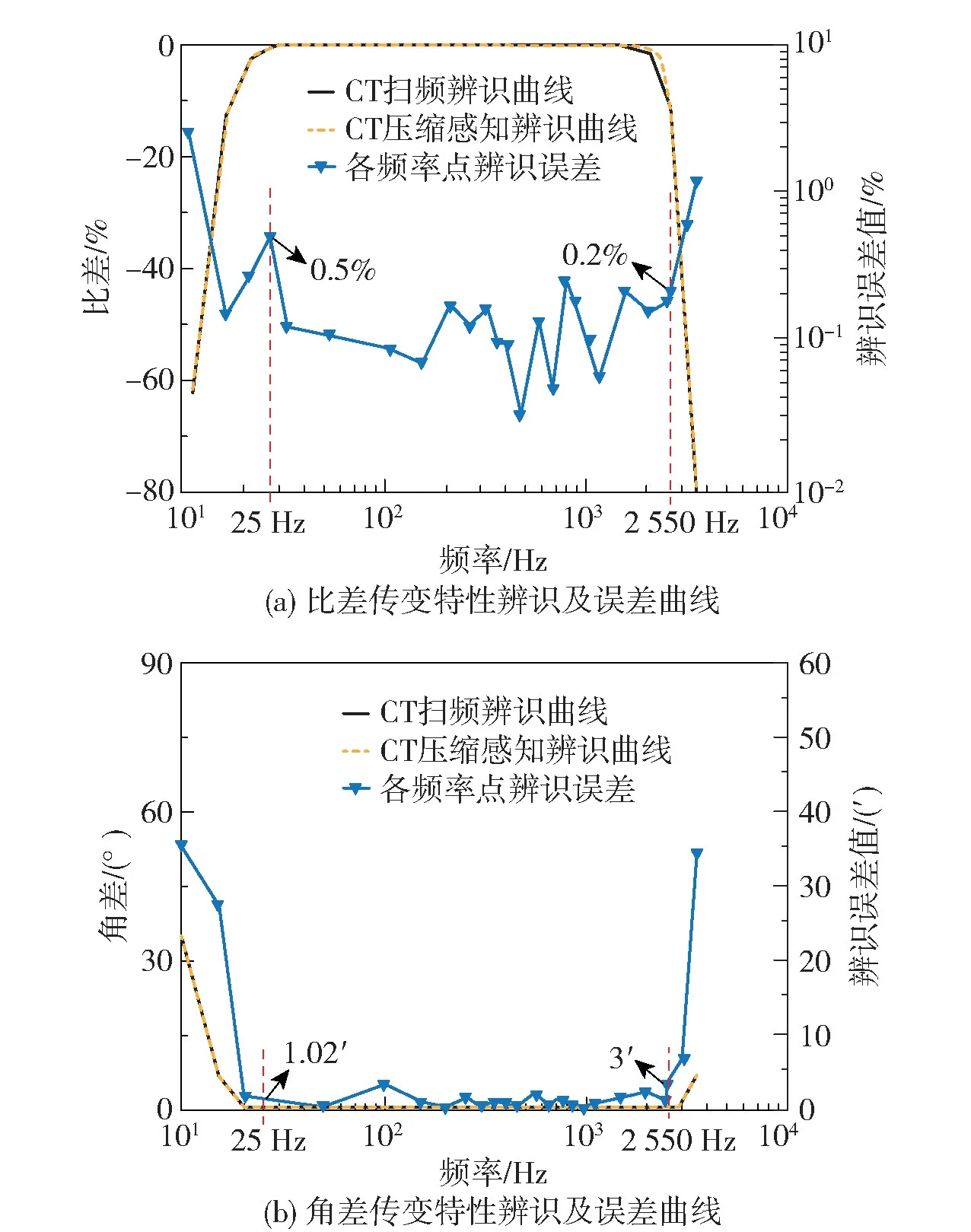
图7 CT 系统辨识及误差曲线Fig.7 CT system identification and error curves

图7 中,在25 Hz 的1/2 次谐波到2 550 Hz 的51 次谐波范围内,与扫频辨识方法的误差相比,比差传变特性压缩感知辨识方法各频率点辨识相对误差平均值为0.06%,角差传变特性压缩感知辨识方法各频率点辨识相对误差平均值为0.49′。在频率为25 Hz 时,比差压缩感知辨识曲线与扫频辨识曲线之间的相对误差值最大,为0.5%;在频率为2 550 Hz 时,比差压缩感知辨识曲线与扫频辨识曲线之间的相对误差为0.2%。在图7(b)中,当频率为25 Hz 时,角差压缩感知辨识曲线与扫频辨识曲线之间的误差为1.02′;频率为2 550 Hz 时,角差压缩感知辨识曲线与扫频辨识曲线之间的误差值最大,为3′。

上述辨识结果表明,压缩感知辨识误差与扫频辨识误差处于同一量级,扫频辨识传变特性曲线与压缩感知时频域传变特性辨识曲线也具有非常好的一致性。

在谐波电能测量频率范围内,整数次谐波频率点下的CT 扫频系统辨识方法和压缩感知系统辨识方法的二次侧输出电流幅值如表2 所示。