变时滞反馈控制的混合中立型随机延迟微分方程的指数稳定性

刘 琪 兰光强

(北京化工大学 数理学院, 北京 100029)

引 言

带有变时滞反馈控制的混合中立型随机延迟微分方程(HNSDDEs)常被用于系统未来的建模,目前已经被广泛应用于种群生态、神经网络以及激光器动力学等领域。

对于随机系统突然性的结构变化,常采用连续时间马氏链来描述,带有马氏链的随机延迟微分方程即为混合随机延迟微分方程。 文献[1]具体研究了混合随机延迟微分方程,文献[2 -4]则进一步考虑了其稳定性及有界性,文献[5 -7]又扩展到了带中立项的混合随机延迟微分方程的稳定性研究。

然而并非所有系统都是稳定的,因此设计一个合适的反馈控制使不稳定的系统变得稳定很有意义。 相应地,文献[8 -11]研究了系统稳定化问题。其中文献[8]研究了常时滞反馈控制的高阶非线性混合随机时滞微分方程的指数稳定性,文献[9]是在文献[10]的基础上进一步研究了变时滞反馈控制的HNSDDEs 的Lp渐进稳定性和H∞稳定性。

本文采用Lyapunov 函数方法,进一步研究了变时滞反馈控制下的HNSDDEs 的指数稳定性。 文献[8]研究了常时滞反馈控制下的混合随机微分延迟方程的指数稳定性,其所涉及的时滞均为常量,本文进一步将常时滞推广到了函数时滞,并且将受控方程推广到了带有中立项的混合随机延迟微分方程,其难点在于找到时滞δ(t)的上界和利用引理2 处理中立项。 文献[9]研究了变时滞反馈控制的具有时变延迟的高度非线性HNSDDEs 的Lp渐近稳定性和H∞稳定性,但缺少指数稳定性,本文则是通过进一步找到更合适的反馈函数确定了方程的收敛速度,即指数稳定性。

1 基本假设与模型描述

设(Ω,F,{Ft}t≥0,P)是一个带有σ流(满足通常条件)的完备概率空间,{B(t)}t≥0是定义在其上的m维布朗运动,{r(t)}t≥0是右连马氏链且独立于{B(t)}t≥0,S= {1,2,…,N}是其状态空间,Γ=(γij)N×N是其生成算子。

考虑变时滞反馈控制HNSDDE

其中^x(t) =x(t) -N(x(t-τ(t)),t,r(t)),且初值满足

2 主要结论与证明

定义片段过程

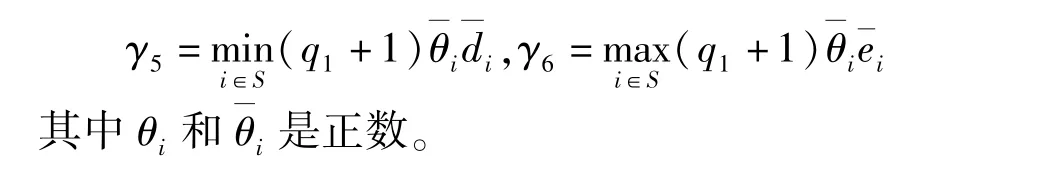
需要注意的是,关于控制函数u的选取,考虑如下特殊情况

其中a＞0,b＞c＞0。 由于|x|2,|y|2的系数均为正数,因此只能得到原方程的矩有界性,而得不到稳定性。 此时可选取u(x,t,i) =Ax,其中矩阵A为实对称正定矩阵,且满足λmax(A) ＜-2a,从而

故加上控制项之后的系统指数稳定。

假设7 存在U∈C2,1(Rn×R+×S;R+),H∈C(Rn;R+),及常数0 ＜α＜1,0 ＜β＜λ,0 ＜λ1,λ2,λ3,ρ1,ρ2,使得对任意的x,y∈Rn,i∈S,t∈R+有

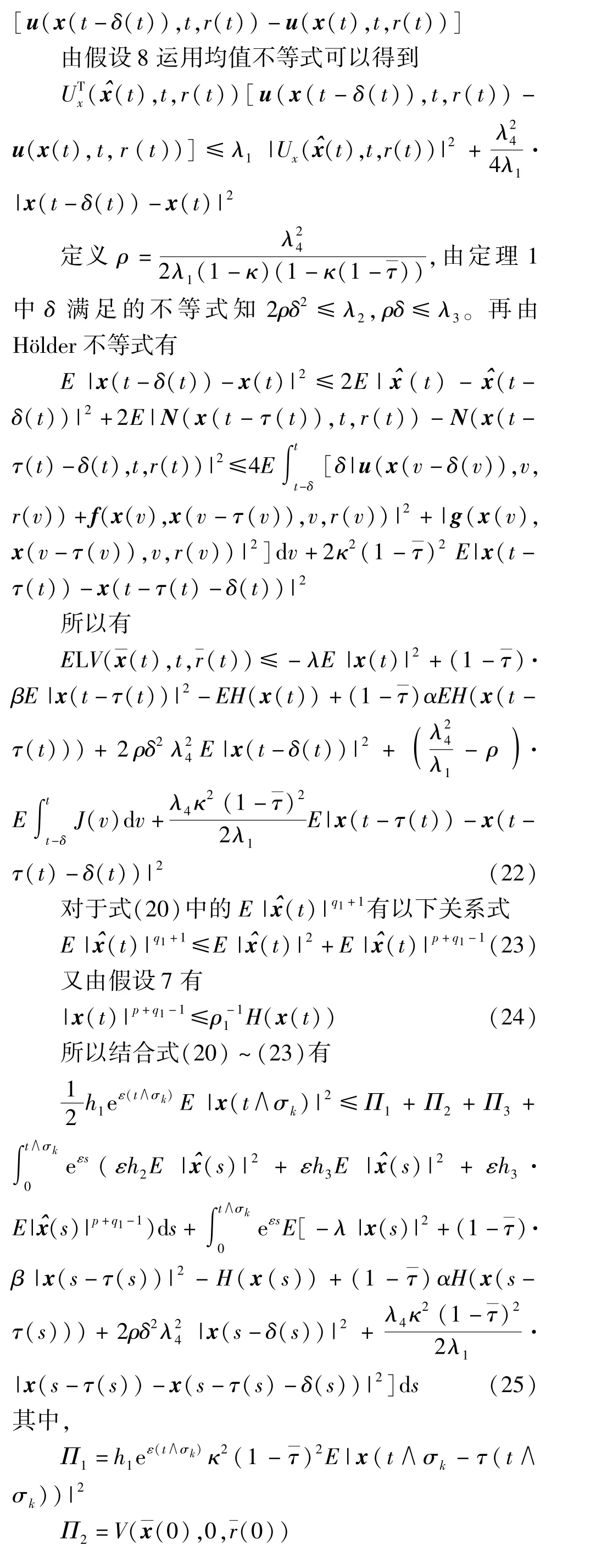
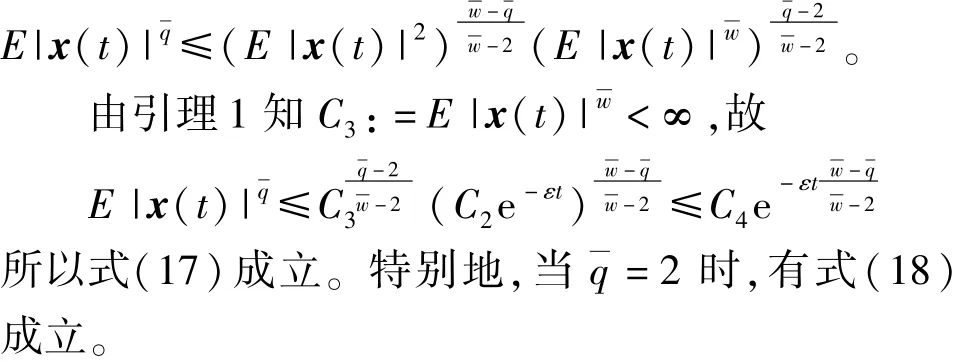
3 例子

考虑一维HNSDDE

由文献[10]可知系统(30)不稳定,以下将通过引入一个反馈控制函数使系统稳定。

增加控制函数u(x,t,1) = -x,u(x,t,2) =-2x,增加控制函数后系统(3)的具体形式为

4 结论

本文采用函数方法,受文献[5]的启发在多项式增长的条件下讨论了变时滞反馈控制下的HNSDDEs 的指数稳定性。 最后,用一个例子证明了结论的有效性。