基于房室模型和WOA-BP 神经网络的药效组分配比计算方法

杨婕妤 李 勇* 向 诚 何子懿

(昆明理工大学1.信息工程与自动化学院;2.生命科学与技术学院, 昆明 650550)

引 言

组分中药是以传统经方为主要研究对象,根据临床疗效确定有效成分,去除无效和毒性成分,将药材中的有效成分进行组合构成的复方药物,这些有效成分既可来自单味中药,也可从中药复方中筛选出来[1]。 组分中药整体综合效应发挥的关键在于药效组分配伍配比的合理性,这对于更好地发挥中药整体效应的特点和优势至关重要[2]。

随着中药研究的不断发展,张伯礼、王永炎院士等[3]提出了一种现代化中药的研究模式,即以组分配伍的思路研究现代中药,这种模式的关键在于如何对各个有效成分进行组合和量化,以获得最佳的配伍比例,从而达到预期的治疗效果,这与组分中药药效组分配比的研究思想是一致的。目前,针对有效成分配比的实验设计方法主要有正交设计[4]、均匀设计[5]、基线等比增减设计[6]、权重配方法[7]、多目标模糊优化法[8]、网络药理学[9]等。 然而,上述实验方法均存在不足:正交设计、均匀设计需要进行大量的实验,以涵盖各种因素组合,从而导致资源和时间的浪费;基线等比增减设计需要选择适当的基线条件,方法较为复杂,并且不同的基线会导致不同的结论;权重配方法需要决策者主观地为各个指标分配权重,使得结果易受个人偏好、经验和主观判断的影响;多目标模糊优化法涉及在多个目标之间找到一组平衡解,这需要大量的计算资源和时间;网络药理学中生物分子之间的相互作用网络是不完整的,存在未知的作用关系,这会导致分析结果的不准确性。中药化学组成成分之所以复杂,是由于其中所含的活性成分种类繁多,不同活性成分之间存在复杂的相互作用,通过已有方法设计筛选出治疗效果较好的组分配比需要进行大量的实验,并且只能找到实验组合中药效相对较好的配比。 因此,开发一种能够减少实验次数、降低实验成本、快速找到药效组分配比的方法成为目前组分中药研究的难点。

随着机器学习研究的不断发展,机器学习模型逐渐应用于中药的配伍机制和剂量等研究领域。 人工神经网络(ANN)是机器学习中常用的模型,具有强大的非线性拟合能力和自学习的特点,针对中药复方研究中面临的复杂非线性问题,ANN 可以建立相应的非线性药效模型,在医药学领域中得到较为广泛的应用[10]。 Zhou 等[11]受中药网络药理学理论的启发,融合表型信息和分子信息,提出了一种基于深度学习的智能配方推荐系统(FordNet),临床评价结果表明,FordNet 可以很好地学习中医专家的有效经验,并获得极佳的推荐结果。 王晓燕[12]利用贝叶斯网络分析了中药寒热药性与正常大鼠药物效应指标的相关性,图形化显示了二者的因果关系和起效通路,并且通过变量指标可进行中药寒热药性预测。金滋力等[13]使用支持向量机(SVM)对方剂配伍数据进行分析,以预测药物配伍的可行性,该方法有助于人们了解哪些药物在配伍时可能会出现不良反应,从而提高方剂的安全性和有效性。 宋小莉等[14]使用反向传播(BP)神经网络构建了一种拟合不同中药配伍与药效学指标(胃黏液含量)之间非线性映射关系的模型,通过该模型可实现对半夏泻心汤及其类似方剂中8 种中药配伍的剂量对胃黏液分泌影响的预测。 吴纯伟等[15]采用均匀设计结合人工神经网络的方法优化脑脉通的组分配伍,使得所设计的脑脉通各组分配比均能不同程度地改善缺血性脑中风的症状。

房室模型是药代动力学研究中采用的一种数学模型,该模型将生物体视为一个系统,按照动力学特性将生物体内部划分为若干房室[16],房室模型的提出旨在将复杂的生物系统进行简化,以便能够定量地分析药物在生物体内的动态过程。 BP 神经网络是一种常见的人工神经网络结构,属于多层的前馈神经网络[17],它可以通过反向传播算法来调整网络参数,以使网络能够逐步逼近目标函数的最优解,可用于解决分类、回归和模式识别等问题。 鲸鱼优化算法(WOA)是一种基于群体智能的算法,受鲸鱼的气泡网捕食机制启发而来,该算法具有操作简单、参数调整少、寻优能力强等优点[18]。 采用WOA 算法对BP 神经网络进行优化,可以有效避免单一BP 算法容易陷入局部最优和预测不稳定等问题,同时还能够提高算法搜索到全局最优解的能力。 为了减少复方配比的实验次数,提高实验效率,本研究提出了利用房室模型结合WOA-BP 神经网络计算中药药效组分配比的方法,通过机器学习来模拟中药组分配比筛选的实验过程,从而达到计算并调整中药组分配比的目的;然后在苯巴比妥(PHB)剂量不变的情况下,以辅助苯巴比妥抑制癫痫的青阳参(Cynanchum otophyllum)药效成分皂苷M1、M2 的配比计算为例进行了实证研究。

1 基于房室模型和WOA-BP 神经网络的药效组分配比分析模型

基于房室模型和WOA-BP 神经网络的中药药效成分配比分析方法的思想来源于BP 神经网络的原理[17]和Box[19]提出的调优运算(EVOP)。 BP 神经网络主要包括正向传播和反向传播两个步骤,在正向传播过程中,输入的样本信号被传递到隐藏层节点和输出层节点,并经过这些节点处的非线性函数作用,最终从输出节点获得网络的输出结果。 如果输出结果与期望输出不一致,则需要建立误差信号,并将其逆向传播回隐藏层和输入层,以便根据误差信号修改网络的权值和节点阈值,以提高网络的输出精度。 这个过程反复进行,直到网络输出误差达到预设的精度要求,从而完成神经网络的训练。本研究的中药药效成分配比分析方法与BP 神经网络的训练过程类似,即将血药浓度作为BP 神经网络的输入,药效作为输出,设置期望药效后会产生误差信号,并通过反向传播修改网络的权值,从而获得期望药效的血药浓度。 EVOP 是以当前运行过程的因子水平为中心,在其周围很近的范围内选定较小变化尺度的因子进行重复试验,并对这些试验结果进行分析;然后对于因子效应的显著性作出判断,将显著因子水平加以调整;最终通过改变基本运行条件来改善响应[19]。 这与本文通过以初始药效为基准,依次设置期望药效以改变药物效应,直至获得能够产生更好药效的血药浓度,然后进一步推导计算出对应配比的思想相符合。

基于房室模型和WOA-BP 神经网络的中药药效成分配比分析流程如图1 所示。 首先基于房室模型建立药效组分的时-量关系,得到药效组分血药浓度所对应的体内药量比例关系;然后基于WOABP 神经网络建立药效组分的量-效关系;最后基于带惩罚系数的WOA-BP 神经网络,利用BP 神经网络的反馈特性,建立药效变化后的药效组分量-效关系,得到药效变化后药效组分的血药浓度,并结合房室模型确定药效变化后血药浓度对应的体内药量比例关系,从而得到药效变化后的给药剂量比(药效组分配比)。

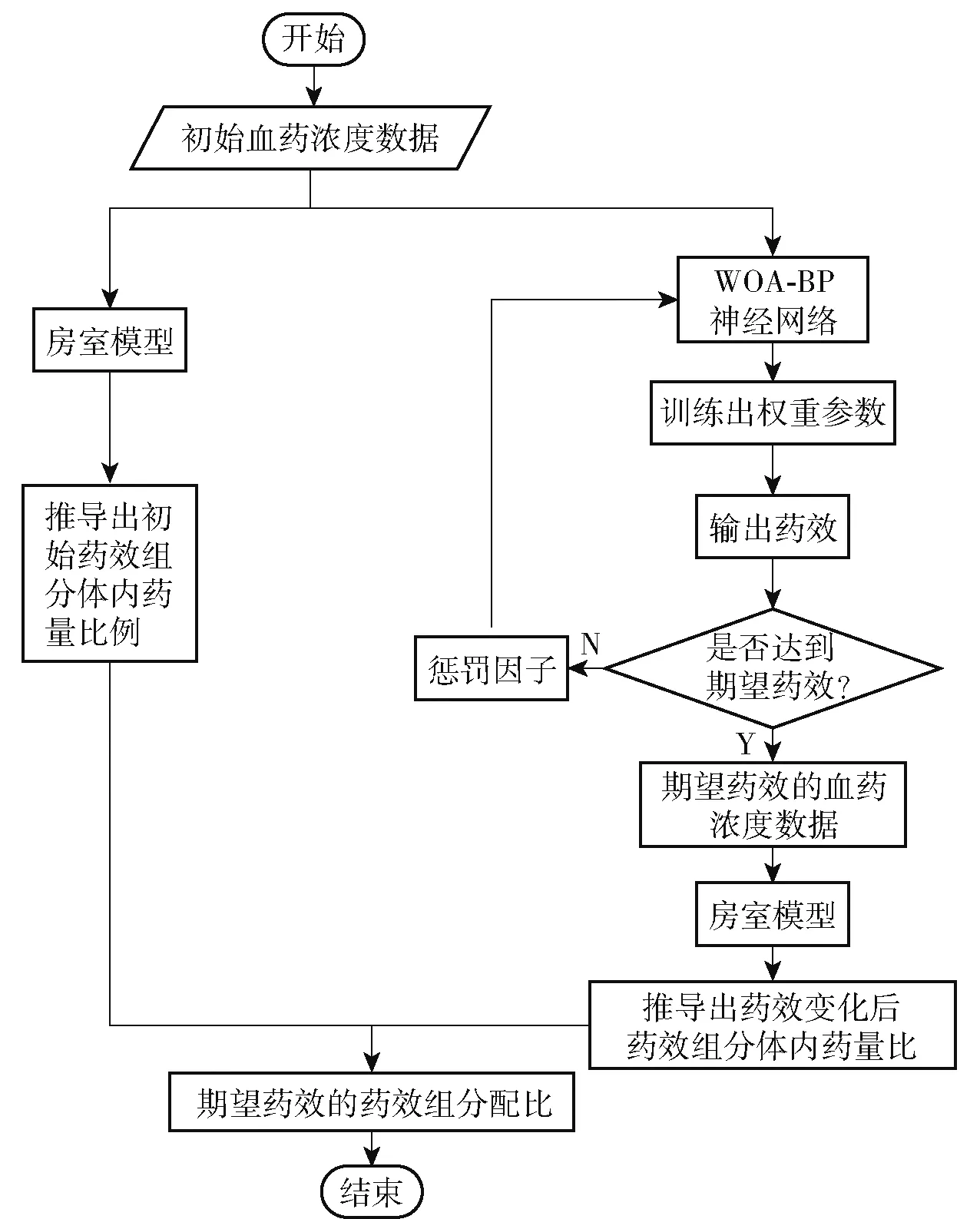
图1 基于房室模型和WOA-BP 神经网络的药效组分配比分析流程图Fig.1 Flow chart of pharmacodynamic component ratio analysis based on a compartment model and the WOABP neural network

1.1 基于单房室模型建立药效组分时-量关系并确定体内药量比例

房室模型是为了定量描述药物体内过程的动态变化规律性而建立的模拟数学模型,它将机体视为一个系统,系统内部按动力学特点分为若干个房室,借助数学的原理和方法来系统地阐明体内药量随时间变化的规律性。 单房室模型是最简单、最常用的房室模型[16],以血管外给药的单房室模型为例,其示意图如图2 所示。

图2 血管外给药的单房室结构Fig.2 Single compartment structure for extravascular administration

单房室药物动力学模型的时-量关系如下:

式中:C(t)为t时刻的血药浓度,α为一级吸收速率常数,β为一级消除速率常数,V为表观分布体积,F为生物利用度,X0为给药剂量,FX0为C(t)对应的药效组分的体内药量。

如果有两种或两种以上的药物组分,其中组分i的单房室药物动力学模型的时-量关系为

式(6)中,Xi,0Fi/Xj,0Fj为药物组分i和j的血药浓度所对应的体内药量比,等式右侧的各项系数可以通过非线性最小二乘法拟合求出。 另外,式(6)只给出了两种不同药效组分的体内药量比,上述推导方法还可以拓展到多种药效组分的体内药量比。

1.2 基于WOA-BP 神经网络建立药效组分的量-效关系

BP 神经网络的基本原理是利用已有的数据集对网络进行训练,用训练好的网络模型对未知数据样本进行输出预测,具有较好的自学习性、自适应性、鲁棒性和泛化性,可广泛应用于模式识别、图像处理等领域。 BP 神经网络主要由输入层、隐藏层和输出层3 部分组成[17],其典型结构如图3 所示,其中:x为输入参数,y为输出,i为输入层中的神经元数,j为隐藏层中的神经元数,k为输出层中的神经元数,w为将输入层连接到隐藏层的权重,v为将隐藏层连接到输出层的权重。

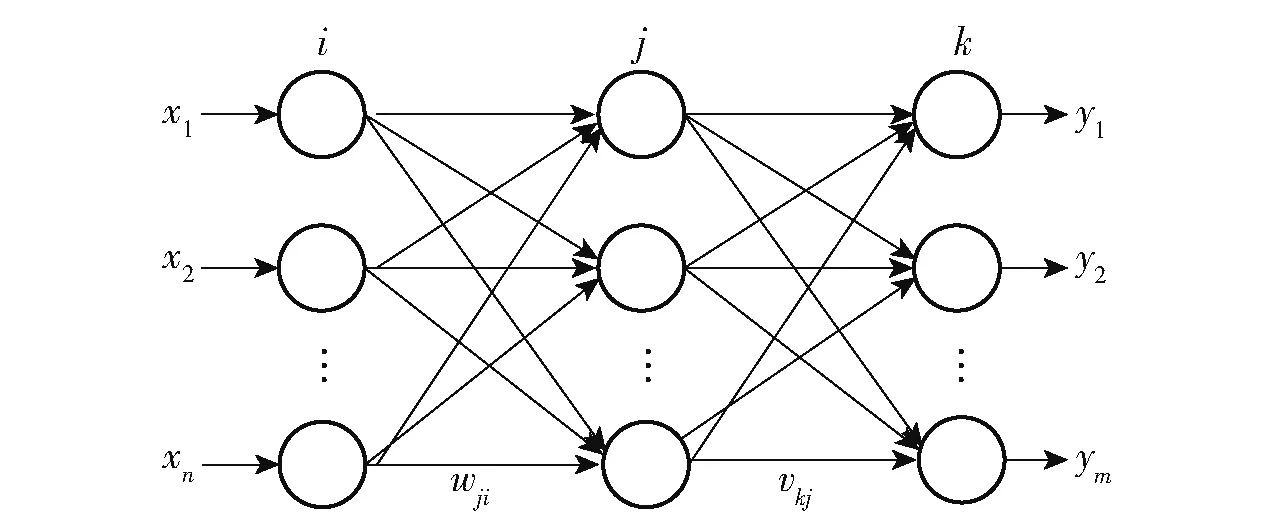
图3 BP 神经网络结构Fig.3 BP neural network structure

WOA 算法通过模拟座头鲸的觅食行为,构建出随机搜索捕食、包围捕食和气泡网捕食等理论模型,以实现对目标问题的优化求解[18],该算法提出的主要数学方程如式(7)所示。

式中:D= |CX*(t) -X(t)|,C=2rp,r是[0,1]之间的随机向量,p是[0,1]之间的随机变量,X(t)和X*(t) 分别为当前鲸鱼的位置向量和每次迭代的最优解;A=2ar-a,a值由2 线性地减小至0,A是在[-a,a] 之间的某随机向量,其值在迭代过程从2 减小到0;D′为第i条鲸鱼的最佳捕食位置,D′ =|X*(t) -X(t) |;b为定义螺旋形状的常数;l为[-1,1] 的随机数;t为迭代次数。

方程(7)模拟出鲸鱼算法中的两种行为:包围机制和气泡网捕猎技术,通过变量p以相等的概率在这两种行为之间进行切换。 在鲸鱼算法中,每一头鲸鱼都代表着一个可行解,而在每一代的游动中,鲸鱼们会随机选择3 种觅食行为向着最优位置的猎物捕猎,或者是通过包围收缩进行位置的更新以逼近目标猎物,直至找到最优解。

将WOA-BP 神经网络的隐藏层封装后可以得到简化的BP 神经网络结构,如图4 所示。 其中:x=[x1,x2,…,xn],表示n个输入参数;y=[y1,y2,…,ym],表示m个输出;w1=[w1,1,w1,2,…,w1,n],表示n个输入参数对输出结果的贡献权重。

图4 简化的WOA-BP 神经网络Fig.4 Simplified WOA-BP neural network

上述模型可以用如下公式表示:

式(8)中:yi(t)为t时刻的输出,x1,x2,…,xn为t时刻的输入参数,w1,1,w1,2,…,w1,n为t时刻输入参数对输出结果的贡献权重。

以各药效组分的血药浓度作为BP 神经网络的输入参数,对应产生的药物效应作为输出,并使用WOA 算法寻找更好的模型参数进行训练,建立初始的药物量-效关系。 具体而言,式(8)中:yi(t)为t时刻的药物效应,包括有效和无效两种状态,分别记为1 和0;x1,x2,…,xn为t时刻输入到网络中的n种药效组分的血药浓度;w1,1,w1,2,…,w1,n为n个输入参数(血药浓度)对输出结果(药物效应)的贡献权重。 为进一步分析不同药效组分对药效的影响,在训练得到的神经网络的基础上,提取网络贡献权重参数,按照各组分对药效的影响程度,得到t时刻药效对应的第i种药效组分整合权重的血药浓度,即整合血药浓度w1,i xi(i∈1,2,…,n)。 使用准确度(accuracy)、精确率(precision)、召回率(recall)、F1-score 这4 个性能指标来评价模型的预测效果。 其中:准确度指所有被正确预测的数据占总数据量的比例;精确率指在所有预测为正例的数据中,实际为正例的比例;召回率指在所有实际为正例的数据中,被预测为正例的比例;F1-score 为精确率和召回率的调和平均。 当神经网络的预测效果较好时,认为该模型是一个符合实际实验结果、能够准确反映各组分量-效关系的模型,可以以此作为初始的药效组分量-效关系模型。

1.3 基于带惩罚系数的WOA-BP 神经网络建立药效提高后的药物量-效关系

基于1.2 节建立的初始的药效组分量-效关系模型,通过输入药效组分的血药浓度预测相应的药效。 在预测过程中,为了输出更多期望的药效状态,在算法中加入了一个惩罚系数Q,对输出的状态给予惩罚,从而实现药效的改变。 具体实现为Q(yi-oi),其中,yi为实际输出,oi为期望输出。 根据实际情况,可以人为调整惩罚系数。 当输出结果改变时,输出层与真实层之间的差值发生改变,利用BP 神经网络反向信号传递的特点,依次向后传播误差,更新输入参数对输出结果的贡献权重,对应的整合血药浓度也发生改变,即可以通过BP 神经网络的反向传播过程,获得药物效应改变时的血药浓度,此时式(8)变为

式中:y′i(t)为药效变化后t时刻的药物效应,与初始模型相比,增加了期望药效状态的输出;x=[x1,x2,…,xn],为t时刻输入到网络中的n种药效组分的血药浓度;w′1,1,w′1,2,…,w′1,n为药效改变后t时刻对应的n种药效组分的贡献权重,此时对应的整合血药浓度为w′1,ixi(i∈1,2,…,n)。 在药效改变后,血药浓度对应的体内药量也随之改变,此时对应药效的组分体内药量比例关系变为

拟合出等式右侧的各项系数后,即可得到药效改变后血药浓度对应的体内药量比。 最后,结合初始药效时各组分血药浓度对应的体内药量比与配比之间的关系,可计算出药效改变后各组分的配比。

2 实验验证

苯巴比妥是临床上治疗惊厥性癫痫的常用药物[20],青阳参对治疗癫痫、慢性肝炎、荨麻疹等疾病有较好的疗效[21],青阳参的主要成分为皂苷M1( Qingyangshengenin 3-O-β-D-oleandropyranosyl-(1→4)- β-D-cymaropyranosyl-(1 →4)-β-D-digitoxopyranoside)和M2(Qingyangshengenin 3-O-β-D-oleandropyranosyl-(1→4)-β-D-cymaropyranosyl-(1→4)-β-D-digitoxopyranosyl-(1 →4 )-β-D-cymaropyranoside),与PHB 联合使用后对治疗癫痫具有协同抑制作用[22]。 青阳参成分M1 和M2 可以增加PHB 的抗癫痫强度,延长作用时间,并且使起效时间提前。临床上青阳参片可以辅助PHB 治疗癫痫,但是有效组分M1 和M2 的配比对药效的影响还有待进一步研究。 本文以辅助苯巴比妥抑制癫痫的青阳参皂苷M1 和M2 的药效组分配比分析为例,来验证所提计算方法的可行性。

2.1 实验材料

小鼠购自湖南松弛精达实验动物有限公司(许可证号:SCXK(滇)K2013-003),体重15 ～22 g,在25 ℃、相对湿度60%的环境中饲养,实验前给予正常饲料和饮水,适应性饲养3 天;青阳参购自昆明中草药市场;PHB 购自上海新亚药业有限公司。 动物实验通过昆明理工大学动物伦理委员会审查,获得伦理许可。

2.2 供试药液配制

将青阳参皂苷M1 和M2 提取[22]后用2%吐温水配制,PHB 用生理盐水配制。 PHB 单独使用时给药剂量为2 mg/L,PHB 与M1、M2 联合使用时PHB、M1、M2 的 给 药 剂 量 分 别 为2 mg/L、12 mg/L、6 mg/L。

2.3 实验数据采集

在128 只小鼠的两耳处涂上生理盐水,用鳄鱼电极夹夹住耳朵,连续电击,对其进行最大电休克(MES)诱导实验。 然后将小鼠分为8 个大组,每组16 只,每个大组再划分为2 个小组,每个小组8 只(即每个时间点的小鼠数量为8 只)。 分别采用PHB 单独给药和联合给药方式进行灌胃,观察0.17 ～24 h 内小鼠的惊厥反应情况:如果给药后后肢不再出现强直性抽搐,说明该药具有抗癫痫作用;如果给药后后肢仍然出现强直性抽搐,说明该药无效;如果小鼠出现死亡,将该组实验数据去掉。 采用液相色谱-串联质谱(LC-MS/MS)体内多组分定量技术[22]测定各组分的血浆药物浓度,结果用均值±标准差表示。 PHB 单独给药和联合给药方式下各组分的血药浓度和惊厥反应分别如表1 和表2 所示。 本研究参考消肿止痛酊的药效学评价方法[23],设定的抑制率为小鼠在某一时间点发生抗惊厥反应的概率,将其作为青阳参抑制癫痫的药效学评价指标,抑制率的计算方法为治疗后无惊厥反应的小鼠数量除以有惊厥反应的小鼠和无惊厥反应的小鼠的数量之和。

表1 小鼠血管外PHB 单独给药方式下PHB 的血药浓度、MES 反应及抑制率Table 1 Plasma concentration of PHB, MES reaction of mice and inhibition rate for extravascular PHB administration alone

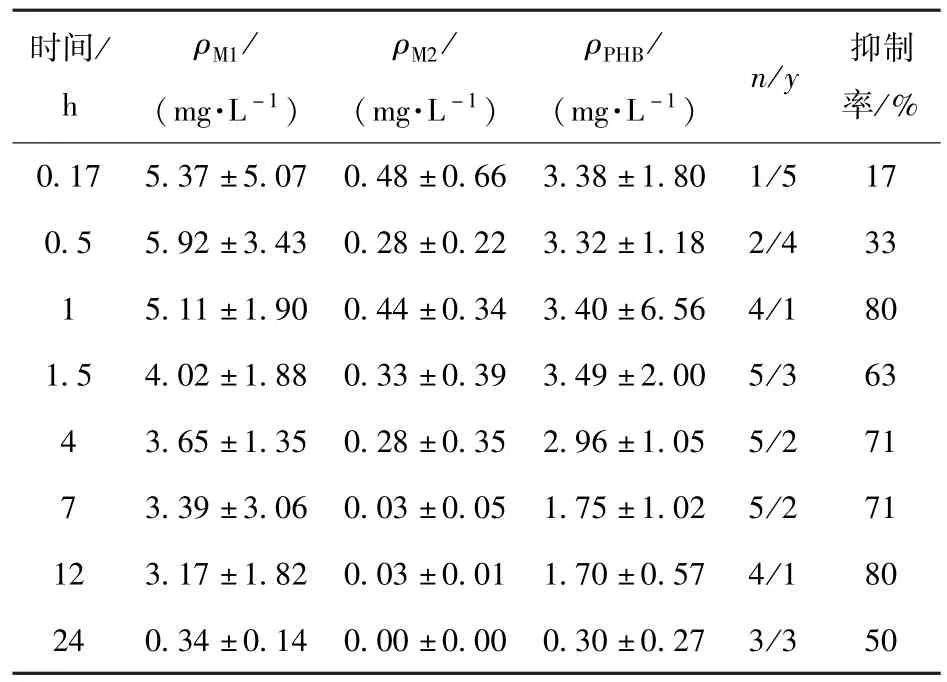
表2 小鼠血管外PHB、M1 和M2 联合给药方式下各组分的血药浓度、MES 反应及抑制率Table 2 Plasma concentration of each component, MES reaction of mice and inhibition rate for the combined administration of extravascular PHB, M1 and M2

2.4 数据预处理

由于实验数据的获取成本较高,获得的样本量较少,因此训练集与测试集的划分存在一定困难,导致小样本的机器学习方法的预测鲁棒性较差。 为了增加样本数量,使得单一的样本具有多样性,本研究采用合成少数类过采样技术(SMOTE)[24]对原始数据进行有效扩充,以增强神经网络的学习能力。 使用SMOTE 方法对表2 的数据进行增强,共得到792组数据,结果见表3。

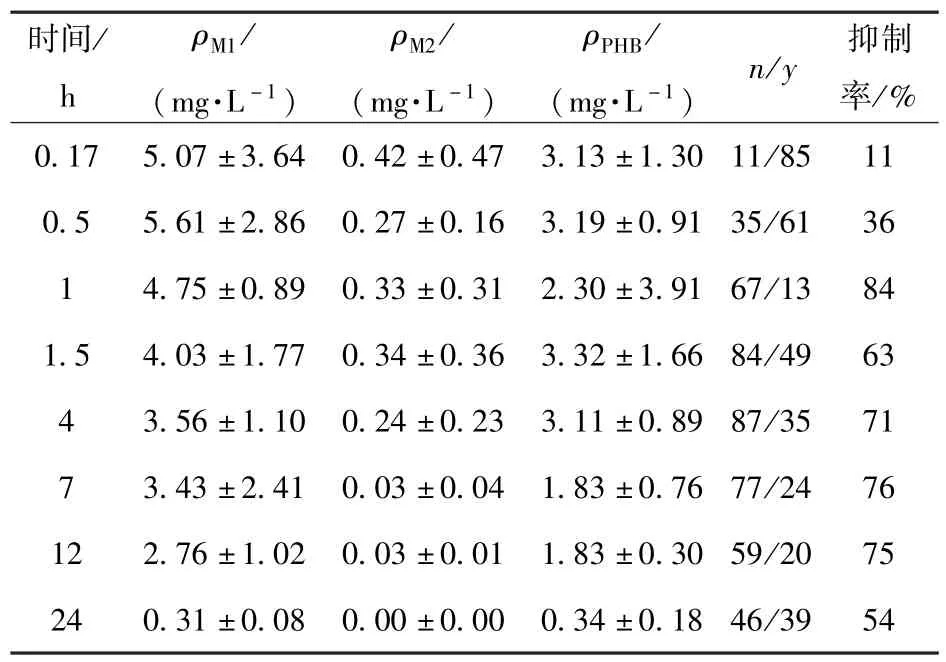
表3 数据扩充后各组分的血药浓度、MES 反应及抑制率Table 3 Plasma concentration of each component, MES reaction and inhibition rate after data expansion

2.5 相关性分析

利用SPSS 软件对上述增强前后的数据进行皮尔逊相关性分析,并结合双尾显著性检验。 在原始数据(表2)中,PHB 质量浓度与M1 质量浓度、M2质量浓度、时间、MES 反应的相关系数分别为0.447、0.280、-0.411、0.268,P值分别为0、0.035、0.001、0.044,整体看,PHB 质量浓度与4 个变量具有相关关系(P＜0.05)。 在增强后的数据(表3)中,PHB 质量浓度与M1 质量浓度、M2 质量浓度、时间、MES 反应的相关系数分别为0.568、0.407、-0.471、0.282,P值均为0,整体看,增强后的数据中PHB 质量浓度与4 个变量具有相关关系(P＜0.05)。 可以看出,原始数据在进行扩充前后的相关系数相差较小,PHB 质量浓度与4 个变量之间的线性关系没有发生显著性变化,能够支撑进一步的分析。

3 结果与讨论

3.1 初始的药效组分体内药量比例关系分析

当多种药物联合使用时,药物之间可能会发生相互作用,使得药效增强或减弱。 这种相互作用一般可以分为协同作用和拮抗作用两种类型:协同作用指当两种或多种药物同时使用时,它们的药效可以相互增强,或者其中一种药物能够增强另一种药物的效果;拮抗作用指当两种或多种药物同时使用时,它们的药效可以相互减弱,或者其中一种药物能够减弱另一种药物的效果。 药代动力学参数指标中,血药浓度-时间的曲线下面积(AUC)代表一次用药后的吸收总量,反映药物的吸收程度。 依据生物等效性原理,在相同的实验条件下,AUC 相同意味着药物效应相同。 通过计算PHB 单独使用以及PHB 与M1、M2 联合使用时的AUC,比较两种给药方式下PHB 药物活性成分的吸收程度有无差异,来考察PHB 与M1、M2 联合给药对PHB 吸收和药效的影响。 根据表1 和表2的数据,使用Phoenix 软件计算得到PHB 单独使用和联合使用时的AUC 分别为31.89 mg·h/L 和40.55 mg·h/L。结果表明,与PHB 单独用药时相比,PHB 与M1、M2 联合使用时,PHB 在小鼠体内的药物吸收程度更大,药效更强,因此M1、M2 与PHB 之间具有协同促进作用。

根据单房室药代动力学模型中血药浓度与时间的关系,使用表3 中的数据,借助非线性最小二乘法拟合得到初始配比下M1 和M2 的药代动力学模型,其时-量关系分别如式(11)和(12)所示,回归分析的决定系数R2分别为0.905、0.860,表明模型的拟合程度较好。

通过拟合得到M1 的α、β和γ分别为11.457、0.072 和5.186,M2 的α、β和γ分别为11.398、0.198 和0.409。 通过式(6)计算出药效未改变时M1、M2 血药浓度对应的体内药量比为12.83∶1。

3.2 WOA-BP 神经网络模型评价

使用表3 中的数据以M1、M2 和PHB 的血药浓度作为输入,药效作为输出,利用BP 神经网络预测对应血药浓度下的药效,建立初始药效下的量-效模型。 采用WOA 算法分别在[0.000 01,0.01]和[100,1 000]的范围内对模型的最佳学习率和迭代次数寻优,其中634 组数据作为训练集,158 组数据作为测试集,得到最佳学习率为0.000 1,迭代次数为700,模型的精确率、召回率、F1-score、准确度分别为0.97、0.98、0.98、0.97。 结果表明,网络的贡献权重能较好地反映出M1、M2 和PHB 的血药浓度对药效的影响,模型能较准确地描述血药浓度与药物效应的关系(量-效关系)。

3.3 药效提高后药效组分配比分析

在3.2 节建立的初始药效下量-效模型的基础上,在预测过程中加入惩罚因子以调整药效,期望输出更多药效组分有效的状态,对输出为无效的状态给予惩罚,将部分输出为无效的状态惩罚为有效状态,以提高有效状态的输出,从而提高药效。 然后通过BP 神经网络的反向传播过程更新M1、M2 和PHB 的血药浓度对药效影响的贡献权重,从而调整对应的整合血药浓度,并将其作为药效提升后对应的血药浓度,建立药效提高情况下的量-效模型。药效提高后各组分的血药浓度、MES 反应及抑制率如表4 所示。

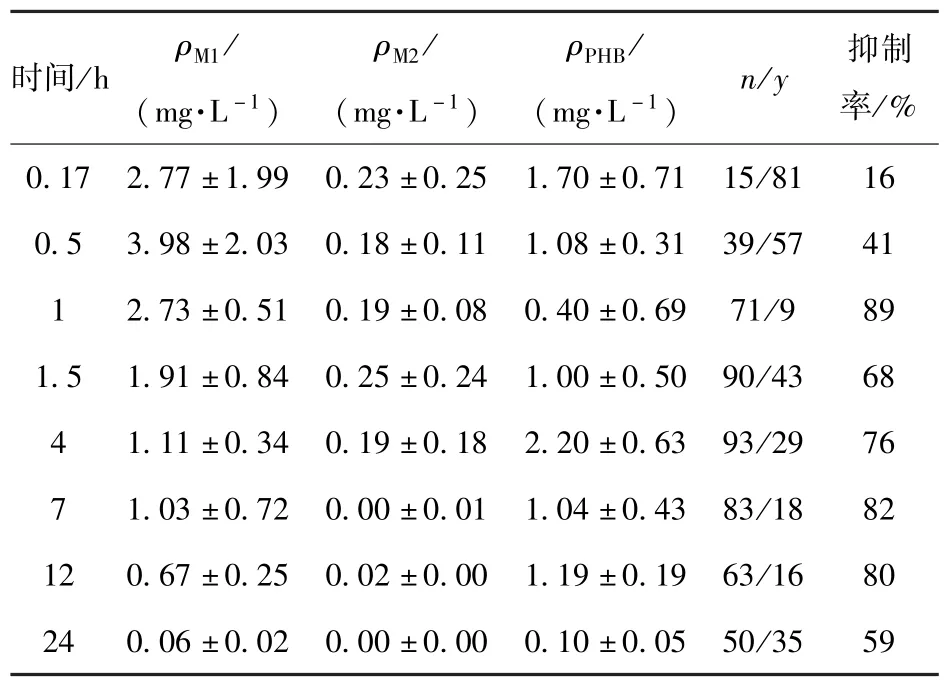
表4 药效提高后各组分的血药浓度、MES 反应及抑制率Table 4 Plasma concentration of each component,MES reaction and inhibition rate after the efficacy was improved

将药效提高后的血药浓度分别作为WOA-BP模型与BP、XGBoost[25]网络模型的输入,对提高后的药效进行预测,经过训练后所有模型的损失函数的误差均趋向于收敛。 表5 为药效提高后不同量-效模型的各项评价指标,可以看出,3 种模型对提高后的药效的预测效果均较好,BP 和XGBoost 模型预测的药效与通过WOA-BP 网络调整后的药效的吻合度较高。 因此,通过WOA-BP 神经网络建立的药效提高后的量-效关系模型,是一个稳定、准确的网络,可以反映实际药效提高后组分的量-效关系变化规律。

表5 药效提高后不同量-效模型的各项评价指标Table 5 Evaluation indexes of different dose-effect models after the efficacy was improved

为了验证WOA-BP 网络的性能,本文使用遗传算法(GA)优化的BP 神经网络(GA-BP)[26]、麻雀搜索算法(SSA)优化的BP 神经网络(SSA-BP)[27]、粒子群算法(PSO)优化的BP 神经网络(PSO -BP)[28]与WOA-BP 进行对比,将药效提高后的血药浓度输入这4 种模型进行药效预测,统计预测准确度和预测时间,结果如表6 所示。 由表6 可知,WOA-BP 和SSA-BP 的预测准确度相同并且略高于GA-BP 和PSO-BP,但WOA-BP 的预测时间更短,效率更高。

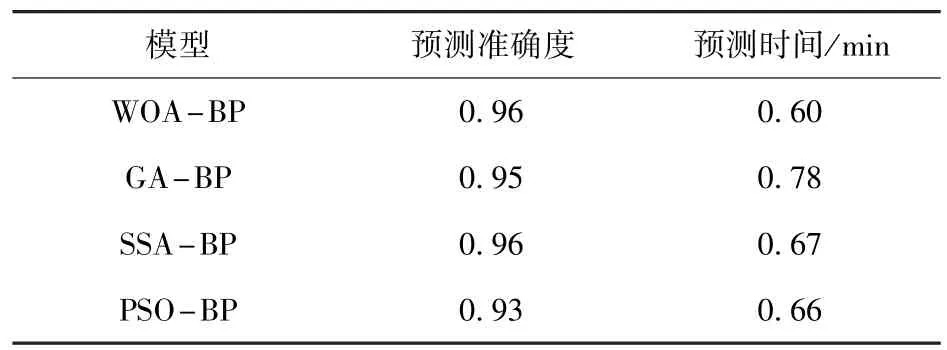
表6 不同模型的性能指标Table 6 Performance indexes of different models

使用表4 中的数据,借助非线性最小二乘法拟合出药效提高后M1、M2 的单房室药代动力学模型,得到药效提高后的时-量关系,分别如式(13)和(14)所示,回归分析的决定系数R2分别为0.863 和0.794,表明模型的拟合程度较好。

通过拟合得到M1 对应的α、β和γ分别为7.503、0.264 和3.776,M2 对应的α、β和γ分别为7.243、0.182 和0.258。 使用公式(10)计算出抑制率提高时M1 和M2 的血药浓度对应的体内药量比为14.49∶1。

未调整药效时,M1、M2 血药浓度对应的体内药量比为12.83 ∶1 时,M1 和M2 的给药剂量分别为12 mg/L 和6 mg/L,即初始配比为2∶1。 相应地可以得出,青阳参的药效增强后,当M1 和M2 的血药浓度对应的体内药量比为14.49∶1时,M1 和M2 的配比为2.26∶1。

基于EVOP 的思想,运用机器学习的方法,对大量的中药配方和功效数据进行分析,寻找其中的规律,并结合房室模型,可以进一步理解中药配比与功效之间的关系。 本文将初始M1 与M2 的配比2∶1作为基准线,利用上述方法进行实验,反复调整药效,最后得到药效提升4%和5%时M1 与M2 的配比分别为2.17∶1和2.26∶1。 基于以上结果,认为M1 与M2 的配比为2.26∶1时,PHB 可以发挥更好的药效。 本文的方法为确定药效与药物配比之间的非线性关系提供了一种途径。

4 结论

本文基于房室模型建立药效组分的时-量关系,推导出药效组分的血药浓度所对应的体内药量比例,利用WOA-BP 神经网络建立药效组分的量-效关系,最后基于带惩罚系数的WOA-BP 神经网络建立药效变化后的药效组分量-效关系,并结合时-量关系得到药效变化后的药效组分配比。 以青阳参皂苷M1 和M2 辅助苯巴比妥抑制癫痫的药效组分配比分析为例,通过建立的基于房室模型和WOABP 神经网络的药效组分配比计算方法,确定了在药效提升5%时M1 和M2 的配比为2.26∶1。

通过WOA-BP 神经网络结合房室模型,可以拟合中药组分配比与功效之间复杂的非线性关系,能够在有限的实验条件下快速确定药效提高时所对应药效组分的配比,避免了大量的实验和时间成本,为中药的配伍研究提供了一种新的方法和思路。 但本文仍存在一些局限,例如只分析了两种药效组分的配比,缺乏实际的临床试验证明该方法在实际应用中的可行性。 今后将会对该方法进行拓展,进一步研究更加复杂的中药组分配比以及中西药结合用药时药效成分配比的计算方法,并对优化后的中药组分配比进行验证。