CIR 利率环境下标的资产带跳的期权定价

李 倩 王 利

(北京化工大学 数理学院, 北京 100029)

引 言

期权定价问题一直都是学者们研究的重点。1973 年,Black 和Scholes 提出了著名的Black -Scholes(B-S)模型[1],给出了欧式期权的定价公式。 在B-S 模型中,标的资产的价格变化过程是连续的,然而这与市场中的数据并不符合。 因此,Merton[2]提出用跳扩散过程来刻画资产的变化,并以无穷项求和的形式给出了欧式期权的定价公式。然而以上两个模型的建立有两个苛刻的假设:一是假设波动率为常数,另一个是假设无风险利率为常数。 为了更好地拟合市场数据,后人在这两个方面作了很多改进。 Heston[3]提出了随机波动率模型,波动率的变化可以用一个随机微分方程来刻画;在此模型的基础上,He 等[4]引入了随机利率,其由Cox-Ingersoll-Ross (CIR)模型[5]给出,即Heston-CIR 混合模型,并给出了欧式期权的定价公式,具体方法是构造远期测度,求出无风险测度下标的资产价格的自然对数的特征函数,以特征函数的形式表示模型的解,并运用傅里叶逆变换求出欧式看涨期权定价,但其标的资产是连续的过程。 黄伯强等[6]利用等价测度变换,推导出了标的资产由Lévy 跳过程驱动的欧式期权定价,但其利率为常数。 毛志娟等[7]利用Δ-对冲和测度变换的方法推导出了当标的资产价格为几何布朗运动时,CIR 利率模型下的欧式期权定价公式,但其标的资产的价格不带跳。南嘉欣等[8]利用计价单位转换原理,推导出了标的资产价格由Lévy 跳过程驱动、利率也由Lévy 跳过程驱动的Vasicek 模型下的欧式看涨期权价格公式,但Vasicek 利率模型不能保证利率为正。

为了规避利率为负的风险,并且鉴于现实金融市场上资产价格跳跃时常发生,本文引入了随机利率(由CIR 模型刻画)和由Lévy 过程驱动的带跳的标的资产模型。 由于多个随机项的存在,要给出欧式期权的显示定价公式是困难的,受文献[2]和文献[4]的启发,我们将两者方法相结合,利用远期测度变换和傅里叶逆变换,给出了级数求和形式的欧式期权定价公式。 并利用数值模拟说明该级数是收敛的,且收敛的速度非常快。 紧接着通过实证分析,与经典的Black-Scholes 模型进行对比,表明了本文模型更符合实际市场。

1 CIR 利率模型与带Lévy 跳的标的资产价格

记(Ω,F,Ft{0≤t≤T},Q)为概率空间,满足通常条件,Q是风险中性概率测度,以下所有随机过程均定义在此概率空间中。

1.1 CIR 利率模型

CIR 模型是一个连续时间状态下的广义均衡模型,利率r(t)的随机微分方程是一个单平方根过程

式中,k、a、σr均为常数,k为均值回归的速度,a为长期均值,σr＞0 为波动率,{W1(t)}t≥0为标准布朗运动。

1.2 带Lévy 跳的标的资产价格

在风险中性测度Q下,标的资产价格S(t)满足以下随机微分方程。

2 相关引理

引理1 Doleans -Dade 指数公式[9]如果X(t)是一个跳扩散过程,则满足初始条件为ZX(0) =1且dZX(t) =ZX(t-)dX(t)的随机微分方程的解为

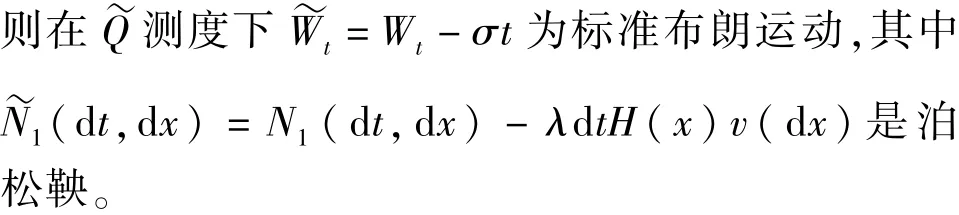
3 欧式期权定价

3.1 定价方法

考虑到期日为T、执行价格为K的欧式看涨期权。 在风险中性测度下,欧式看涨期权的价格U(S,r,t)实际上是收益期望的现值

式中,b(t,T,r(t))是在风险中性测度Q下到期日为T的零息债券的价格,这意味着首先要计算出b(t,T,r(t))以及利率和资产价格在远期测度QT下所满足的随机微分方程。

定理1 若利率r(t)由式(1)给出,则到期日为T的零息债券在时刻t的价格b(t,T,r(t))为

b(t,T,r(t)) =exp{A(t,T) +G(t,T)r(t)},0≤t≤T

其中,

利用文献[13]的结论,可知零息债券的价格是利率的指数仿射函数,所以假设b(t,T)满足以下形式

3.2 定价公式的推导

在远期测度QT下,可以得到到期日为T、执行价格为K的看涨期权的价格为[11]

证明 为了推导式(22),首先需要知道f(ϕ;t,T,z,r)的定义,它满足

4 数据模拟

本节检验定价公式的收敛速度是在限制条件式(20)下选择的参数,为了方便编程计算,取跳跃幅度(Y-1)为固定的跳跃幅度0.01,其中σr=σ=0.05,k=2,a=0.05,r0=0.03,S0=110,K=100,λ2=1,到期时间τ=0.5。 图1 给出了标的价格的变化路径。 图2 表示D(ϕ;τ)级数的阶数为n+1和n时W(S,r,τ)的绝对差,可以看出当级数的阶数达到临界点时,绝对差变为0,并且从该时刻起,无论级数的阶数有多大,绝对差一直保持为0,则W(S,r,τ)可以视为是收敛的。 因此,当增加级数的阶数时,绝对差急剧减小到0 的现象表明W(S,r,τ)收敛非常快,所以在计算W(S,r,τ)时,可以将D(ϕ;τ)级数的阶数取为10,此时绝对差为10-4。

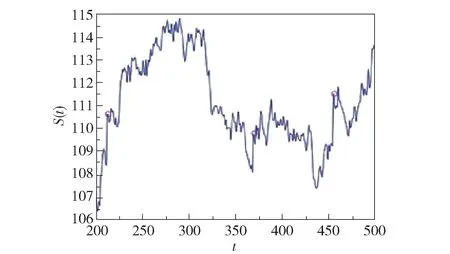
图1 标的价格的变化路径Fig.1 The path of S(t)

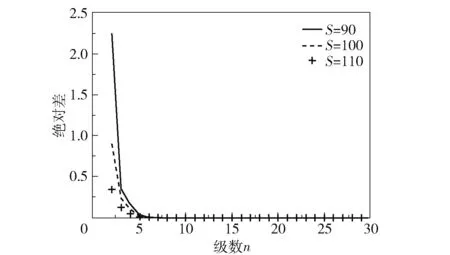
图2 D(ϕ;τ)级数的阶数为n+1 和n 时W(S,r,τ)的绝对差Fig.2 Absolute difference of W(S,r,τ) between the n+1-term and n-term

图3 给出了U(S,r,τ)级数的阶数为m+1 和m时的绝对差。 当m=7 时,其绝对差为10-4,因此U(S,r,τ)级数的阶数取值为7 时可以看作是收敛的。

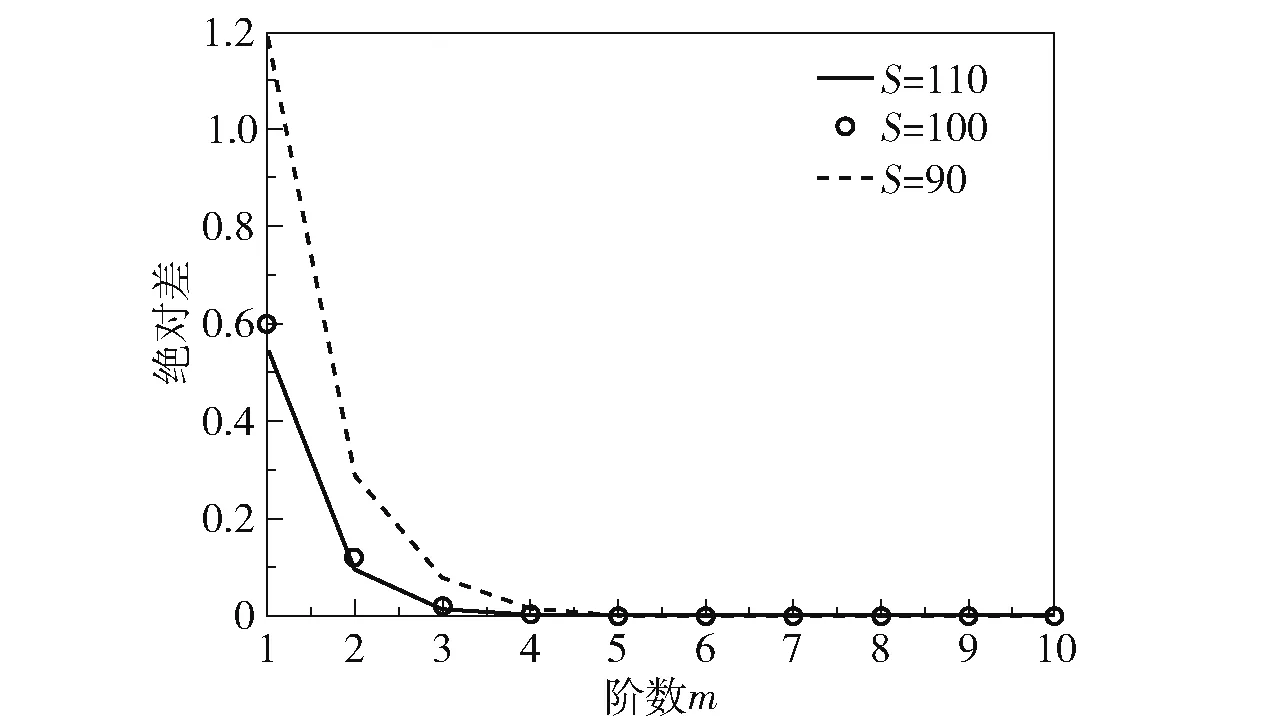
图3 U(S,r,τ)级数的阶数为m+1 和m 时的绝对差Fig.3 Absolute difference of U(S,r,τ) between the m+1-term and m-term

改变跳跃幅度,检验U(S,r,τ)级数是否还是收敛。 设跳跃幅度Y服从对数正态分布,即lnY～N(0.01,0.009)。 利用Matlab 生成Y的随机数,其他参数不变,图4 给出了U(S,r,τ)级数的阶数为m+1 和m时的绝对差,当m=7 时,其绝对差为10-4,说明U(S,r,τ)是收敛的,则此时的期权价格可以被视为收敛的期权价格。

图4 U(S,r,τ)级数的阶数为m+1 和m 时的绝对差Fig.4 Absolute difference of U(S,r,τ) between the m+1-term and m-term

为了验证所选模型的有效性,根据文献[14]的数据(2020 年5 月27 日的上证50ETF 认购期权交易数据)进行实证分析。 参数的选取说明如下。4 月20 日该期权的标的资产价格为2.8,即S0=2.8。 4 月20 日距5 月27 日到期日35 天,故T=35/365=0.095 9;根据4 月20 日的上海银行间同业拆放利率,取r0=0.016 74;根据华夏上证50ETF 的历史价格得到年化波动率为0.233 6, 即σ=0.233 6,同时设σr=σ=0.233 6;设CIR 利率模型中的k=0.012,a=0.021;跳跃幅度为固定跳跃幅度Y=1.01。 将所选模型下定价公式模拟计算出的结果与真实值和B-S 模型定价公式给出的理论值进行比较,结果如表1 所示。

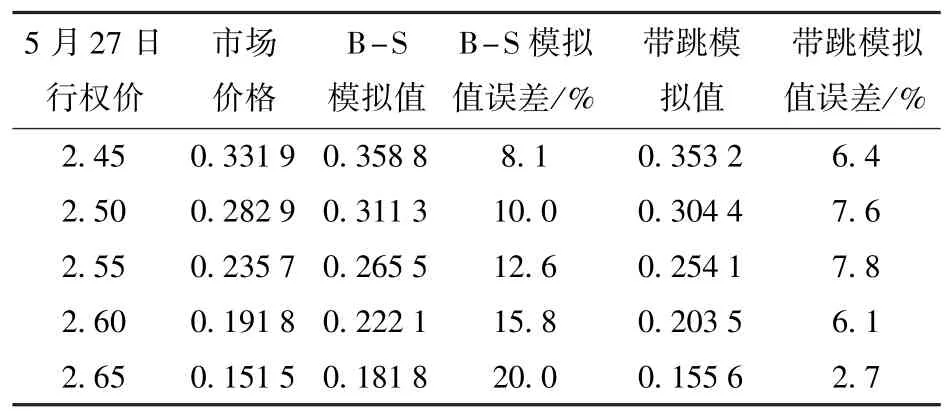
表1 模型模拟数值结果与B-S 模型理论值的对比Table 1 Comparison of model simulation numerical results with B-S model theoretical values

通过数值模拟可以看出,本文模型模拟出的数值解与真实值之间的误差控制在8%以内,且相较B-S模型,本文模型的准确度更高,更符合实际市场情况。

5 结束语

本文采用混合模型,即包含带Lévy 跳的标的资产模型和CIR 利率模型,给出了级数形式的欧式期权的定价公式。 通过Matlab 数值模拟证明了解的收敛性,实证分析结果也验证了本文模型的数值解比经典的B-S 模型定价结果更准确。