“多边形的面积”复习教学，应关注空间维度

王加林

摘 要：教学“多边形的面积”后，设计一节复习（拓展）课，引导学生重新推导平行四边形、三角形、梯形的面积公式，梳理多边形面积公式之间的关系，进而归纳发现面积的二维属性，类比发现周长的一维属性，并发散认识空间的维度，从而帮助学生更好地理解面积概念，区分周长与面积，发展空间观念。

关键词：小学数学；面积；周长；空间维度；多边形的面积

一、教前思考

周长和面积是小学数学中比较容易混淆的两个概念。学生（使用苏教版小學数学教材）在三年级上学期学习周长概念以及长方形和正方形的周长，在三年下学期学习面积概念以及长方形和正方形的面积，然后在五年级上学期学习平行四边形、三角形、梯形等多边形的面积。教学面积概念后，可以从定义和度量两个角度，引导学生比较辨析周长和面积的联系和区别。时隔一年半，教学“多边形的面积”后，学生对“周长和面积的联系和区别”掌握得如何？笔者在课后作业中设计了一道有关周长和面积的练习：

把一个用铁丝围成的长方形框架拉成一个平行四边形，该框架的周长和面积发生了什么变化？

对此，笔者所教班级以及同年级其他班级学生的答题情况统计如下页表1所示。可见，学生的错误率不低，这反映出他们对周长和面积的联系和区别掌握得不是很好。进一步访谈得知：学生知道周长和面积的描述性定义、度量方法以及计算方法（数或算出度量单位的个数），有比较好的量感；但是，对二者度量本质（联系）下的空间维度属性（区别）理解得不透彻。

实际上，“几何学起源于图形大小的度量……根据图形的维数，把度量一维图形大小的数称为长度，将二维图形的大小用面积来表示……”［1］。但是，小学数学教材对长度、面积等的维度属性介绍得并不多。张奠宙先生就曾指出：小学教材中对长度、面积和体积的维度属性认识不足，导致学生对线段、平面、立体的区分及关联有些疏漏，甚至出现错误。［2］

因此，教学“多边形的面积”后，笔者设计了一节复习（拓展）课，引导学生重新推导平行四边形、三角形、梯形的面积公式，梳理多边形面积公式之间的关系，进而归纳发现面积的二维属性，类比发现周长的一维属性，并发散认识空间的维度，从而帮助学生更好地理解面积概念，区分周长与面积，发展空间观念。

二、教学过程

（一）重新推导平行四边形、三角形、梯形的面积公式

教材引导学生通过剪拼的方法把平行四边形转化为长方形，从而得到平行四边形的面积公式；然后，通过拼接两个相同的三角形的方法把三角形转化为平行四边形，从而得到三角形的面积公式；最后，通过拼接两个相同的梯形的方法把梯形转化为平行四边形，从而得到梯形的面积公式。这样做有几个不自然的地方：三角形更简单、更基本，为什么不先推导三角形的面积公式？推导平行四边形的面积公式时，为什么要沿着高剪下（分割）？剪下后，为什么还要移拼？这并不容易想到。推导三角形、梯形的面积公式时，怎么想到“加倍”后拼接？这和推导平行四边形面积公式的思路并不一致。其中最关键的是：高的得出不自然。这不容易让学生感受到高的重要性，进而发现面积的二维属性：两个互相垂直的线段的长度（一维度量）相乘的结果。

因此，笔者引导学生重新推导平行四边形、三角形、梯形的面积公式：回到由面积单位度量得到的长方形面积公式，发现直角三角形的面积是其一半；对于一般三角形，想到作高将其分割为两个直角三角形；对于平行四边形，想到作高将其分割为两个直角三角形和一个长方形；对于梯形，想到作高将其分割为两个直角三角形和一个长方形。这样不仅使思路更自然，而且凸显了高的重要性，有利于学生发现面积的二维属性。

（二）归纳总结，发现面积的二维属性

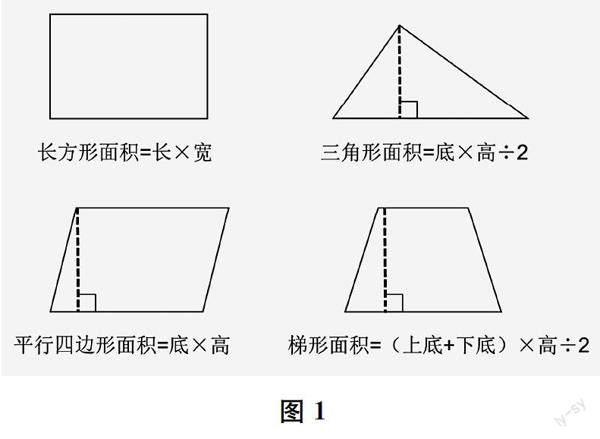
师 我们学习了长方形、三角形、平行四边形以及梯形的面积公式。（出示图1）观察这几个图形及其面积公式，说一说它们有什么相同之处？

生 我发现，长方形和平行四边形的面积公式都是将水平方向的长度与垂直方向的长度相乘。比如，长方形的长表示图形水平方向的长度，宽表示垂直方向的长度，相乘得到面积；平行四边形的底表示图形水平方向的长度，高表示垂直方向的长度，相乘得面积。

生 我发现，三角形的面积公式也有这样的特点：将两个互相垂直的长度，也就是底和高相乘。

师 那为什么计算三角形的面积还要除以2呢？

生 三角形的面积是转化成平行四边形或长方形来计算的，它的面积是转化后的平行四边形或长方形的一半。

师 很好！那梯形的面积公式呢？是不是也有这样的特点？

生 我觉得，梯形的面积公式也可以这样理解：“上底+下底” 其实是一个量，就是水平方向的长度；高则是垂直方向的长度。它除以2的原因和三角形是一样的。

师 没错！由此，我们可以发现面积的二维属性：所有平面图形的面积归根到底都是其中互相垂直的两个线段的长度（即两个维度）相乘的结果。

有了多个平面图形的面积公式，归纳总结其共性，发现面积概念度量本质下的二维属性，正当其时。由此，学生可以深刻理解面积概念，特别是面积的量纲，以及说平面是二维的、称平面图形为二维图形的道理。

（三）类比迁移，发现周长的一维属性

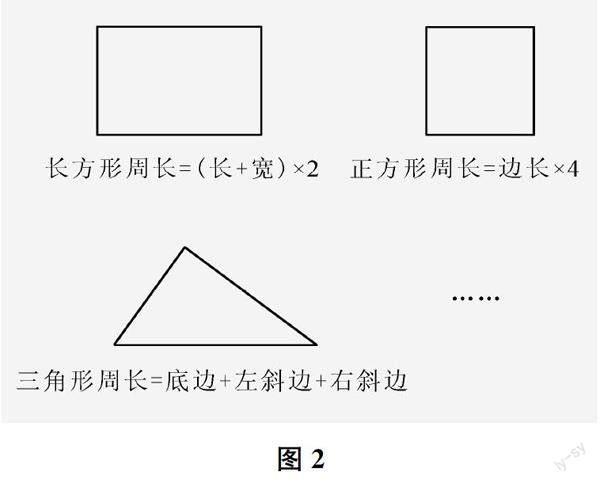
师 同学们，我们发现了平面图形面积的二维属性。那我们之前学习过的周长呢？（出示图2，省去了平行四边形、梯形的周长计算）来回顾一下周长公式，其中有什么秘密？

生 我发现，长方形的周长是长与宽的和乘2，公式中有长与宽两个相关量；正方形的周长是边长乘4，公式中只有边长这一个相关量；三角形的周长是三条边相加，有三个相关量。这三个图形的周长公式好像没有什么共同点。

……

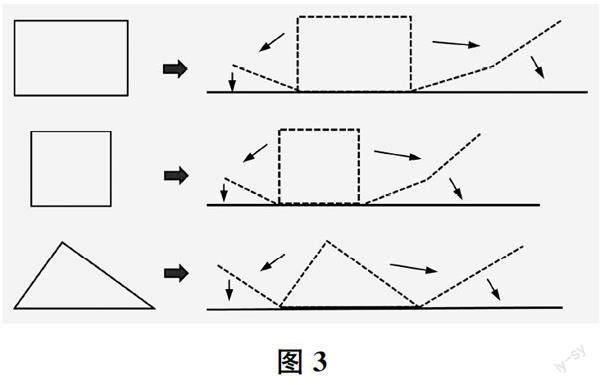
师 同学们，其实周长就是图形一周的长度之和。（出示图3）我们可以把长方形、正方形、三角形的周长像这样展开，得到一条长长的线。类比面积的二维属性，你有什么发现？

生 周长就是一些线段的长度之和。虽然这些线段的方向不同，但是我们可以把这些线段像这样展开到同一个方向，如此，周长就是这些线段连起来后的线段的长度了。

师 是的。也即是说，周长归根到底是一条线段的长度。这就是周长的一维属性。現在，你能很好地区分周长和面积了吗？

生 面积是二维的，它是图形中互相垂直的两个长度相乘的结果。周长是一维的，它是图形中一些线段的长度之和。

认识了面积的二维属性，类比迁移到周长的维度属性，发现其是一维的，能帮助学生进一步理解面积（二维）与周长（一维）的区别，掌握图形维度的含义。在学生观察公式没有发现共性的情况下，教师适时演示周长的展开，激活了学生的思维，促进了学生对周长一维属性的理解。

（四）发散联系，进一步认识空间的维度

师 同学们，大约在五六千年前，古埃及人在测量土地时，就认识到要从长和宽两个维度来认识面积，由此慢慢地产生了几何学。后来，《几何原本》中，就有“线段是一维的，以长度来度量；平面图形是二维的，以面积来度量；立体图形是三维的，以体积来度量”的内容，初步有了维度概念。那么，你在生活中有没有看到过或听到过有关维度的内容？

生 我经常去电影，3D电影就是三维的，因为看普通电影时，我们只能从屏幕上感受到上下、左右两个维度的方向；而看3D电影时，还能感受到前后这个方向，有的人物就像是从画面上走出来的，离你越来越近。

生 我有一次看科学展，看到了3D打印机，它打印出来的东西不像普通打印机打印出来的那样只在平面上，而是立体的，很真实，也就是三维的，有前后、左右和上下三个维度的方向。

师 其实，我们的数学教材中也有许多关于一维、二维、三维的知识，你发现了吗？

生 我们学过确定位置，一年级学习的确定位置只在一个方向上，是一维的；四年级学习的是在平面上确定位置，是二维的，用数对表示——数对中一个数表示行，是水平方向的；另一个数表示列，是垂直方向的。我觉得，将来还会学习在立体空间中确定位置，即三维的。

师 是的。在立体空间中确定位置要用到三个维度，不仅要表示前后、左右，还要表示上下。

认识了一维和二维，自然可以拓展到三维。学生在生活中早就看到过或听到过维度以及一维、二维、三维的说法，但是对它们的理解还不是很到位。因此，本环节联系历史、生活和数学学习，让学生进一步理解维度，从而激发学生的学习热情，为中学进一步学习有关维度的知识（如平面直角坐标系和空间直角坐标系、平面向量的基底和空间向量的基底）做好铺垫。

参考文献：

［1］ 吴正宪，刘劲苓，刘克臣.小学数学教学基本概念解读［M］.北京：教育科学出版社，2014：325.

［2］ 张奠宙.浅而不错、分而不碎，着眼于数学素质的养成——以“维度”概念为例［J］.小学教学（数学版），2014（12）：4-6.