基于遗传粒子群算法风电机组变速与变桨系统PI控制器设计

2023-12-08刘颖明张书源王晓东柏文超

科学技术与工程 2023年31期

刘颖明, 张书源, 王晓东, 柏文超

(沈阳工业大学电气工程学院, 沈阳 100870)

现役运行的风电机组在变速与变桨系统中普遍采用比例积分(proportional integral, PI)控制策略[1-2]。PI控制因结构简单,容易数字化等特点而被广泛应用[3]。然而,由于PI控制参数不精确和恒定的PI控制参数将导致风电机组无法在全风速段实现精确控制[4]。此外,如何兼顾提升控制精度和降低载荷情况的问题亟需解决[5-6]。因此,研究风电机组变速与变桨系统PI控制器设计方法有着重大意义。

目前,国内外学者对风电机组变速与变桨系统PI控制器设计做了大量研究。利用频域特性进行系统辨识的方法被广大研究者不断的改进。文献[7]采用的辨识方法忽略了时延特性差异,造成变速与变桨系统辨识的精度较低。基于时域特性整定PI控制参数的方法依然被广泛应用。文献[8]通过阶跃响应整定的PI控制参数对复杂工况的适应性较差。文献[9]根据工程中通用的方法整定PI控制参数。但PI控制参数的精确度不高,需要根据实际情况进一步优化。智能算法因适用性强,搜索精度高的特点而被广泛应用在优化控制参数的领域。文献[10]中仅以提升发电机转速控制精度为目标优化控制参数,但并未考虑风电机组所经历的载荷情况。文献[11]中采用的优化方法并没有考虑湍流风随机种子和湍流强度对优化结果所造成的影响。文献[12]在优化时忽略了控制目标之间的权重,导致提升控制精度和降低载荷情况难以兼顾。文献[13]基于正交试验设计确定权重关系时,需要进行大量实验才能确定各因素对结果的影响关系,导致效率低下。文献[14]中利用遗传算法优化控制参数时,由于种群多样性较差往往容易陷入局部最优,从而导致优化不充分。文献[15]中因粒子群算法的收敛性较差,导致在优化控制参数时搜索的时间过长。近年来,随着控制理论的发展,自适应控制得到了深入研究。文献[16]提出的自适应控制需要更换风电机组中现有的控制器,所带来的巨大经济成本将导致在实际的工程中无法得到广泛的推广和应用。

综上所述,为提升风电机组的控制精度并降低关键承载部件的载荷情况,现提出基于遗传粒子群算法的变速与变桨系统PI控制器的设计方法。考虑风电机组变速与变桨系统的时延特性差异,分别采用不同的系统辨识方法和PI控制参数整定方法。并提出了基于帕累托分配权重的方法,从而兼顾提升控制精度和降低载荷情况的控制目标。同时,考虑湍流风随机种子和湍流强度的影响,提出了基于遗传粒子群算法优化各平衡点变速与变桨系统PI控制参数的方法。最终,提出了能够根据外部风况变化计算和切换PI控制参数的变速与变桨系统自适应PI控制。

由仿真验证的结果可知,在变速控制中能够有效提升输出功率并抑制塔架顶部侧向振动,在变桨控制中能够有效平抑输出功率和发电机转速波动并降低叶片根部载荷情况。

1 控制原理与数学模型建模

1.1 变速与变桨系统控制原理

风电机组运行在额定风速以下的恒转速区采用变速控制。变速系统PI控制根据发电机转速额定值ωrate与测量值ωmea之间的差值Δω输出给定的发电机转矩T。风电机组运行在额定风速以上的恒功率区采用变桨控制,变桨系统PI控制根据Δω输出给定的桨距角β。变速与变桨PI控制结构如图1所示。其中:GT(s)为变速系统,输入和输出分别为发电机转矩和发电机转速;GP(s)为变桨系统,输入和输出分别为桨距角和发电机转速;Kp_T、Ki_T为变速系统PI控制参数;Kp_P、Ki_P为变桨系统PI控制参数。

PI控制器结构表达式为

(1)

式(1)中:u(t)为控制量;e(t)为误差;Kp和Ki分别为比例和积分系数。

图1 风电机组变速与变桨控制Fig.1 Wind turbine speed and pitch control

1.2 变速与变桨系统数学模型建模

由Garrad Hassan (GH)公司开发的权威风电机组仿真软件Bladed现已通过德国船级社和IEC认证,成为公认的行业标准之一[17]。现以Bladed软件中2 MW风电机组物理模型为基础构建变速与变桨系统的数学模型,其主要参数如表1所示。

考虑到风电机组的非线性特性,为便于整定PI控制参数需要获得其线性系统[18]。因此,基于Bladed软件将2 MW风电机组物理模型在各平衡点采用泰勒级数展开。将非线性风电机组线性化为多输入多输出(multiple-in multiple-out, MIMO)的状态空间方程,即

表1 2 MW风电机组主要参数Table 1 Main parameters of 2 MW wind turbine

(2)

式(2)中:A、B、C、D为三维矩阵,第三维为平衡点;x为状态变量;u为输入变量;y为输出变量。

其中,选取变速与变桨控制范围内步长为1的风速点作为平衡点,其余步长为0.1的风速点均定义为远离平衡点。

考虑到风电机组的参数随风况变化,为便于整定PI控制参数需要构建特定平衡点的单输入单输出(single-input single-output, SISO)数学模型[19]。因此,通过提取MIMO系统中输入、输出和平衡点构建特定风速时的传递函数。

以风速11 m/s时的变速系统GT(s)和风速16 m/s时的变桨系统GP(s)为例完成数学模型建模,表达式分别为

GT(s)=[-0.016 673(s2+0.063 09s+8.513)(s2+0.167 5s+20.81)(s2+9.724s+378.4)×(s2+0.743 9s+449.6)(s2+0.607 3s+558.7)]/[(s+0.065 99)(s2+0.038 08s+8.879)(s2+2.116s+196.2)(s2+5.289s+450)(s2+1.379s+524.6)(s2+2.466s+627)]

(3)

GP(s)=[0.000 273 68(s+619.4)(s-9.922)(s+12.85)(s2-0.062 32s+8.596)(s2+0.097 54s+9.176)(s2+1.124s+99.19)×(s2+3.728s+312.4)(s2+9.724s+378.4)×(s2+0.283 8s+545.7)(s2+0.355 2s+783.3)×(s2-126 2s+6.713×106)]/[(s+3.333)(s+0.138 8)(s2+0.359 3s+8.887)(s2+0.038 35s+8.881)(s2+3.941s+46.26)(s2+2.007s+193.2)(s2+3.459s+345.3)(s2+5.511s+462)(s2+1.257s+522.6)(s2+2.331s+635.8)(s2+4.964s+427 2)]

(4)

式中:GT(s)表示风速为11 m/s时代表转矩-转速的变速系统;GP(s)表示风速为16 m/s时代表桨距-转速的变桨系统。

基于泰勒级数展开和提取输入、输出和平衡点的方法构建2 MW风电机组其余各平衡点的变速与变桨系统数学模型。

2 系统辨识和PI控制参数整定

2.1 变速与变桨系统控制原理

考虑到变速系统具有较大的惯性,分别采用Pade法和Routh法将GT(s)辨识为低阶惯性系统。其中,基于Pade法改进获得的Routh法理论上具有更高的系统稳定性和辨识精度[20]。

Routh法将待辨识的系统展开成式(5)的形式,Fj(s)的详细表述为式(6)的形式,进而根据Routh表确定的参数辨识出所需阶次的低阶惯性系统。

(5)

(6)

式中:ɑi、βi为待定系数,可直接由Routh表查表求得。G(s)为辨识后的传递函数;Fj(s)为展开分式;n为辨识后传递函数的阶次。

分别采用Pade法和Routh法对GT(s)辨识得到低阶惯性系统GT_Pade(s)和GT_Routh(s),表达式为

(7)

(8)

GT_Pade(s)和GT_Routh(s)与变速系统GT(s)开环阶跃响应对比如图2所示。

由Pade法和Routh法辨识得到的GT_Pade(s)和GT_Routh(s)均能反映变速系统GT(s)的主要特征。在保证系统稳定的基础上,辨识精度高达99.88%和99.94%。因此,选用辨识精度更高的Routh法将变速系统GT(s)辨识为低阶惯性系统GT_Routh(s)。

考虑到变桨系统具有较大的时延,分别采用传递函数(transfer function, TF)法和最小二乘(least squares, LS)法将GP(s)辨识为惯性时延系统表达为

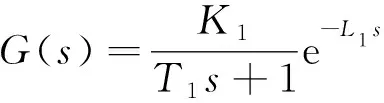
(9)

式(9)中:K1为终值;L1为延迟;T1为上升时间。

其中,由于LS法的稳定性辨识精度均能满足辨识要求,因此通常适用于复杂系统的辨识[21]。LS法原理表达式为

z(k)=hT(k)θ+e(k)

(10)

式(10)中:z(k)为第k次输出测量值;h为样本;θ为待辨识参数;e(k)为噪声。

取准则函数表达式为

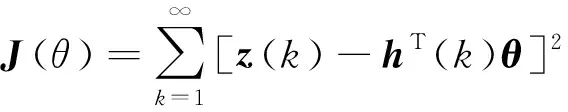
(11)

当准则函数输出的偏差平方累计值达到最小时,可以获得辨识的惯性时延系统。

分别采用TF法和LS法对GP(s)辨识得到惯性时延系统GP_tf(s)和GP_least(s),表达式为

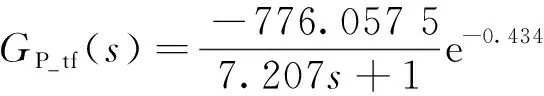
(12)

(13)

GP_tf(s)和GP_least(s)与变桨系统GP(s)开环阶跃响应对比如图3所示。

图3 变桨系统开环阶跃响应Fig.3 Open loop step response of variable pitch system

由TF法和LS法辨识得到的GP_tf(s)和GP_least(s)均能反应变桨系统GP(s)的主要特征。在保证系统稳定的基础上,辨识精度高达99.76%、99.89%。因此,选用辨识精度更高的LS法将变桨系统GP(s)辨识为惯性时延系统GP_least(s)。

2.2 变速与变桨系统PI控制参数整定

以11 m/s变速系统经辨识获得的GT_Routh(s)作为受控系统,并基于两种不同的误差积分准则整定变速系统PI控制参数,其具体的表现形式如表2所示[22]。

基于ITSE和ITAE整定的变速系统PI控制参数的闭环阶跃响应如图4所示。

表2 误差积分准则Table 2 Error integral criterion

图4 变速系统闭环阶跃响应Fig.4 Closed-loop step response of variable speed system

两种方式整定的变速系统PI控制参数均可以达到控制要求。ITSE的优点在于上升时间相对较短,但最重要的衡量指标超调量却达到15%。然而,ITAE的调整更加迅速并且可以将超调量降低到3%。因此,选择ITAE整定的变速系统PI控制参数作为初始值。

以16 m/s变桨系统经辨识获得的GP_least(s)作为受控系统,并基于Ziegler-Nichols (Z-N)法和Chien-Hrones-Reswick (C-H-R)法整定变桨系统PI控制参数。

Z-N法通常需要由阶跃响应计算斜率ɑ=K1L1/T1,进而整定变桨系统PI控制参数。C-H-R法是在其基础上改进获得的[23],因允许受控系统中带有较大阻尼而具有广泛的适用性。

基于Z-N法和C-H-R法整定的变桨系统PI控制参数的闭环阶跃响应如图5所示。

两种方式整定的变桨系统PI控制参数均可以达到控制要求。Z-N法的优点在于上升时间较短的同时调整更加的迅速,但超调量却达到16%。然而,C-H-R法可以实现零超调。因此,选择C-H-R法整定的变桨系统PI控制参数作为初始值。

分别采用Routh法和LS法辨识其余各平衡点的变速与变桨系统。然后分别基于ITAE和C-H-R法整定其余各平衡点的变速与变桨系统PI控制参数初始值。

图5 变桨系统闭环阶跃响应Fig.5 Closed-loop step response of variable pitch system

3 PI控制参数优化和自适应PI控制构建

3.1 遗传粒子群算法优化PI控制参数

为提升风电机组的控制精度并降低关键承载部件的载荷情况,需要对各平衡点变速与变桨系统PI控制参数的初始值进一步优化。然而,遗传算法(genetic algorithm, GA)由于种群多样性较差容易陷入局部最优,粒子群算法(particle swarm optimization, PSO)由于收敛性较差而导致效率低下。因此,提出一种将GA的交叉和变异操作引入PSO中,获得兼具全局和局部搜索性能的遗传粒子群算法(genetic algorithm particle swarm optimization, GAPSO)优化各平衡点的变速与变桨系统PI控制参数。GAPSO可以保证搜索前期的种群多样性从而防止陷入局部最优,同时还可以保证搜索后期的快速收敛性从而提升算法效率。

GAPSO参数设置如下[24-25]:种群规模M=50,代数G=50,个体学习因子C1=2,群体学习因子C2=2,惯性权重w=1.6,交叉概率Pc=0.8,变异概率Pm=0.1。GAPSO算法结构如图6所示。

基于GAPSO优化各平衡点的变速与变桨系统PI控制参数的具体步骤如下。

图6 GAPSO结构Fig.6 GAPSO structure

(1) 对种群进行初始化,并设定运行参数。为提升控制参数在完整风电机组中的适应性,将MIMO系统当作受控系统。考虑复杂风况对控制参数优化结果的影响,以不同的湍流风随机种子和湍流强度为输入设计对照试验。并将各平衡点变速与变桨系统PI控制参数的初始值作为起始值。

(2) 计算全部个体的目标函数值,从而记录个体和种群最优。在变速控制中,由于气动转矩与电磁转矩存在差异将造成塔架顶部侧向振动。因此,变速系统的目标函数FT由发电机转速和塔架顶部侧向加速度两部分构成,如式(14)所示。在变桨控制中,桨距角频繁发生变化将造成叶片根部的载荷加剧。因此,变桨系统的目标函数FP由发电机转速和桨距角两部分构成,如式(15)所示。其中,发电机转速反应控制精度,塔架顶部侧向加速度和桨距角均反应载荷情况。

(14)

(15)

(16)

(17)

(18)

(3) 根据目标函数值的计算结果,对种群中的个体进行排序和筛选。保留优秀的个体,并淘汰较差的个体。同时,更新个体的速度和位置。

(4) 通过交叉操作和变异操作产生新的种群。

(5) 再次计算全部个体的目标函数值,从而更新个体和种群最优。

(6) 判定目标函数值是否保持稳定或达到最大种群代数。若是或达到,则输出变速与变桨系统PI控制参数。否则,重新进入到步骤(2)中。

目标函数FT、FP均由两部分构成,需要通过帕累托(Pareto)分配权重ξ、η,从而达到兼顾提升控制精度和降低载荷情况的目标。以变速系统目标函数FT的权重ξ为例,其对应风况下的Pareto如图7所示。

(19)

(20)

以GAPSO优化11 m/s变速系统PI控制参数为例,在湍流风速下目标函数FT变化如图8所示。

随着目标函数值逐渐减小,证明PI控制参数的精确性得到不断提升。通过对比图8(a)和图8(b)、图8(c)和图8(d),目标函数值受到随机种子的影响较小,代表基于GAPSO优化的PI控制参数对各种类型的湍流风均有出色的适应性。通过对比图8(a)和图8(c)、图8(b)和图8(d),由于风电机组的参数随风况不断变化,较大的湍流强度会导致GAPSO优化的PI控制参数无法达到最佳。因此,选择湍流强度为0.1时基于GAPSO优化的变速系统PI控制参数Kp_T、Ki_T。同理,可以获得变桨系统PI控制参数Kp_P、Ki_P。

图7 不同风况下ParetoFig.7 Pareto under different wind conditions

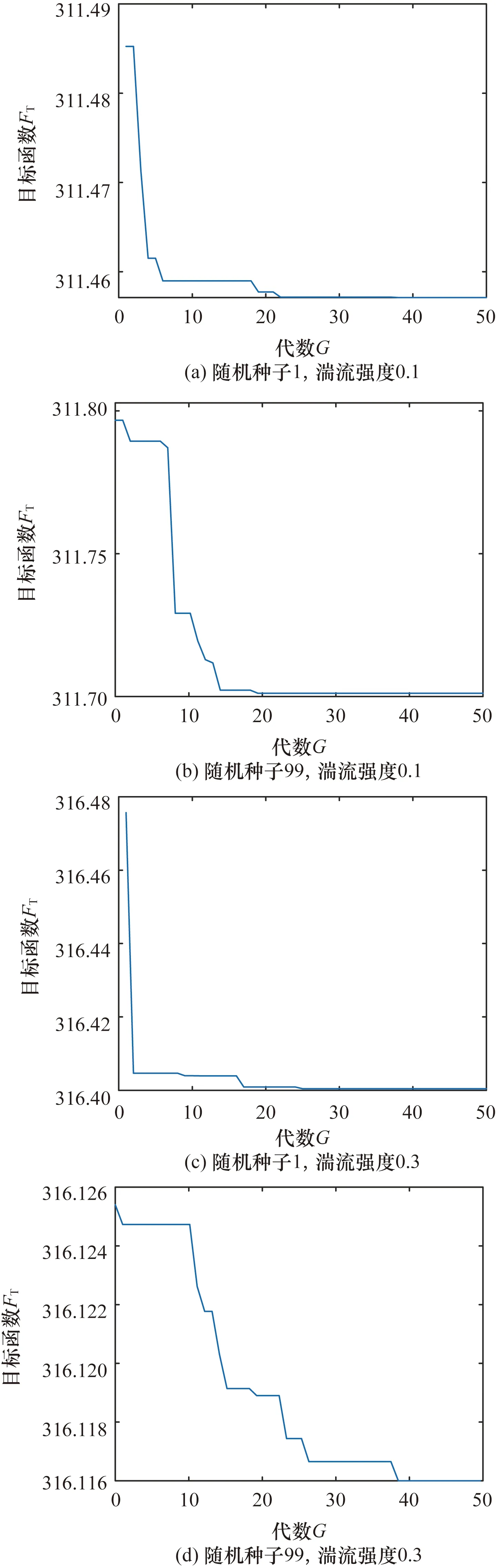
图8 不同风况下目标函数Fig.8 Objective function different wind conditions

基于GAPSO优化其余各平衡点的变速与变桨系统PI控制参数。

3.2 构建自适应PI控制

变速与变桨系统PI控制参数设计在平衡点处,然而大量的远离平衡点处并没有设计控制参数。当风电机组的运行远离平衡点时,在平衡点设计的变速与变桨系统PI控制参数将不能提供出色的控制性能[26]。因此,为提升风电机组远离平衡点时的控制性能,针对变速与变桨控制的特性,分别提出了对应的自适应PI控制。

在变速控制时,风电机组的参数跟随风况持续变化。因此,提出了由平衡点离散的变速系统PI控制参数和风速拟合构建变速系统自适应PI控制的方法。风速与各平衡点的变速系统PI控制参数如表3所示。

将表3中变速系统PI控制参数和风速采用LS法进行拟合,构建变速系统自适应PI控制,表达式为

Kp_T(v)=35.1v2-598.2v+2 991

(21)

Ki_T(v)=10v2-158v+832

(22)

式中:Kp_T(v)和Ki_T(v)为变速系统比例和积分系数的风速函数;v为风速。

比例和积分系数的风速函数拟合精度分别达到99.97%和99.95%,满足拟合精度的需求。变速系统自适应PI控制变化曲线如图9所示。

表3 变速系统参数Table 3 Variable speed system parameter

图9 变速系统自适应PI控制曲线Fig.9 Adaptive PI control curve of variable speed system

分析图9可知,当风电机组的运行远离平衡点时,可以通过构建的变速系统自适应PI控制计算和切换远离平衡点的控制参数,从而为风电机组提供出色的控制性能。

在变桨控制时,风电机组根据不同的风况通过调节桨距角实现额定功率输出。由于风电机组能够对桨距角实现准确的测量。因此,提出了由平衡点离散的变桨系统PI控制参数和桨距角拟合构建变桨系统自适应PI控制的方法。风速与对应的桨距角关系由Bladed软件中2 MW风电机组提供,并结合各平衡点的变桨系统PI控制参数制成表4。

将表4中变桨系统PI控制参数和桨距角通过LS进行法拟合,构建变桨系统自适应PI控制,表达式为

Kp_P(β)=-0.155β3+0.223β2-

0.128β+0.032

(23)

Ki_P(β)=0.125β3-0.096β2+

0.006β+0.012

(24)

式中:Kp_P(β)、Ki_P(β)为变桨系统比例和积分系数的桨距角函数;β为桨距角。

比例和积分系数的桨距角函数拟合精度分别达到99.92%和99.85%,满足拟合精度的需求。变桨系统自适应PI控制变化曲线如图10所示。

分析图10可知,数据点紧密的分布在变桨系统自适应PI控制的变化曲线附近。因此,可以通过构建的变桨系统自适应PI控制计算和切换远离平衡点的控制参数,从而为风电机组提供出色的控制性能。

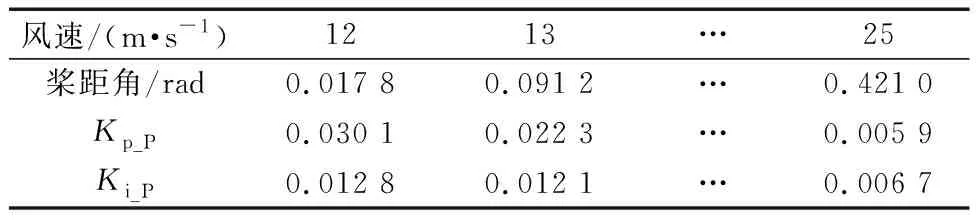
表4 变桨系统参数Table 4 Variable pitch system parameter

图10 变桨系统自适应PI控制曲线Fig.10 Adaptive PI control curve of variable pitch system

4 算例分析

以2 MW风电机组为例进行算例分析。并根据卡曼模型和国际电工委员会标准定义三维风流场,从而生成湍流风工况等仿真环境。本文所采用的三种控制策略如表5所示。

通过比较控制策略1、2和3,验证基于GAPSO优化能够进一步提升变速与变桨系统PI控制参数的精确性并显著降低关键承载部件的载荷情况。

表5 算例分析中的控制策略Table 5 The control strategy in the example analysis

4.1 变速系统自适应PI控制效果

4.1.1 控制精度分析

当仿真环境为9 m/s的湍流风时,风电机组采用变速控制,9 m/s湍流风如图11所示。

输出功率和发电机转速的控制效果是衡量控制精度的指标。该工况下输出功率和发电机转速如图12、图13所示。

由图12、图13分析得到的性能指标情况如表6所示。

与控制策略1相比,控制策略3的输出功率平均值提升2.21%,其标准误差均方根误差降低10.67%。同时,发电机转速均方根误差降低7.28%。与控制策略2相比,控制策略3的输出功率平均值提升1.31%,其均方根误差降低6.89%。同时,发电机转速均方根误差降低5.62%。上述结果显示:GAPSO相较于GA和PSO优化变速系统PI控制参数可以提升输出功率,并平抑输出功率和发电机转速的波动。

图11 9 m/s湍流风工况Fig.11 9 m/s turbulent wind condition

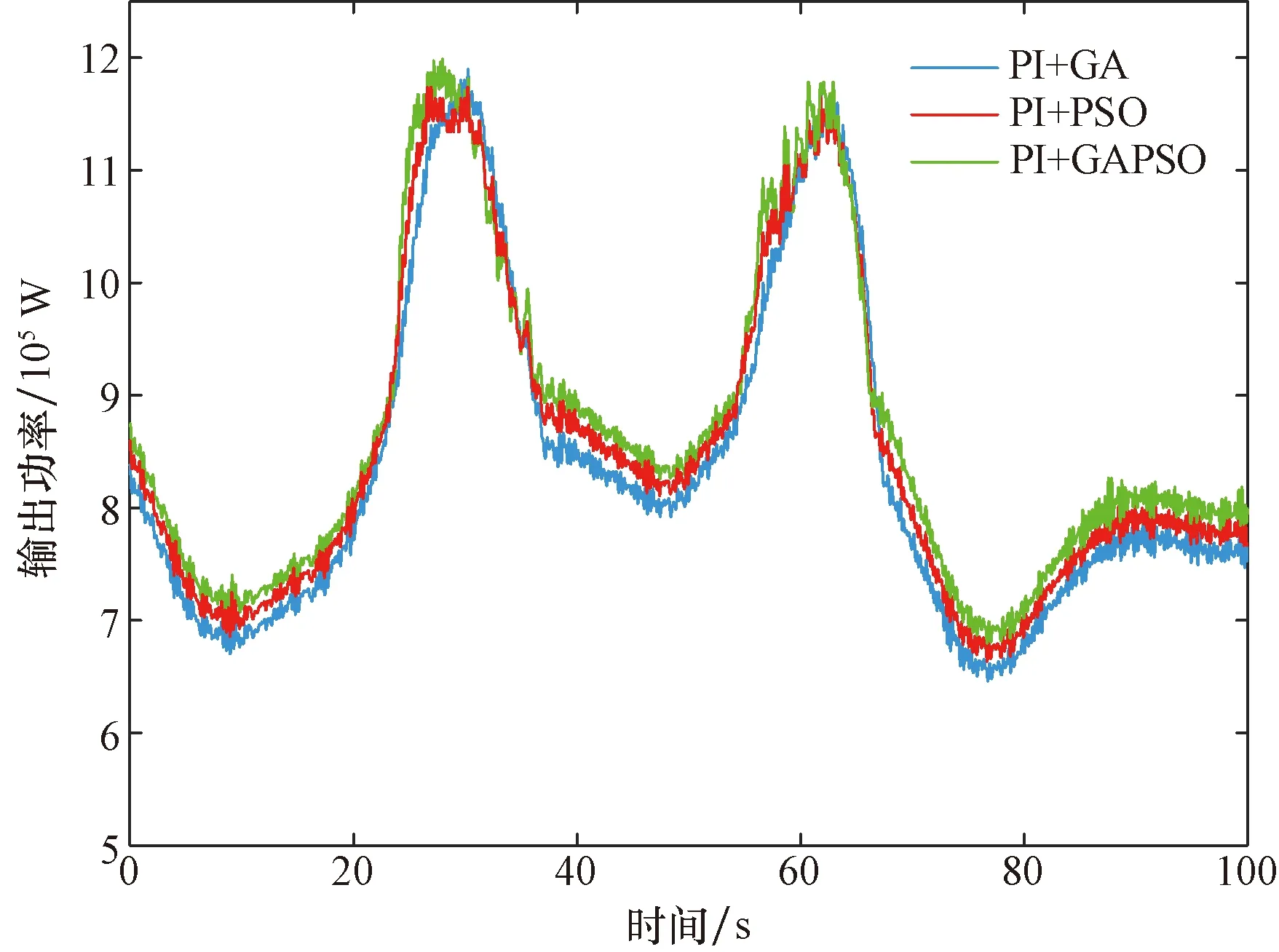
图12 输出功率比较Fig.12 Comparison of output power

图13 发电机转速比较Fig.13 Comparison of generator speed

表6 控制精度比较Table 6 Comparison of control accuracy

4.1.2 塔架顶部侧向振动分析

塔架顶部侧向速度和加速度控制效果是衡量塔架顶部侧向振动的指标。塔架顶部侧向速度和加速度分别如图14、图15所示。

由图14、图15分析得到的性能指标情况如表7所示。

与控制策略1相比,控制策略3塔架顶部侧向速度极差极差、平均值分别降低44.71%、33.41%。同时,塔架顶部侧向加速度极差、平均值分别降低44.21%、33.16%。与控制策略2相比,控制策略3塔架顶部侧向速度极差、平均值分别降低26.03%、20.73%。同时,塔架顶部侧向加速度极差、平均值分别降低25.98%、20.24%。上述结果显示:GAPSO相较于GA和PSO优化变速系统PI控制参数能够有效抑制塔架顶部的侧向振动。

图14 塔架顶部侧向速度比较Fig.14 Comparison of tower top side-side velocity

图15 塔架顶部侧向加速度比较Fig.15 Comparison of tower top side-side acceleration

表7 塔架顶部侧向振动比较Table 7 Comparison of side-side vibration of tower top

4.2 变桨系统自适应PI控制效果

4.2.1 控制精度分析

当仿真环境为15 m/s的湍流风时,风电机组采用变桨控制,15 m/s湍流风如图16所示。

输出功率和发电机转速的控制效果是衡量控制精度的指标。该工况下对应的输出功率和发电机转速如图17、图18所示。

由图17、图18分析得到的性能指标情况如表8所示。

图16 15 m/s湍流风工况Fig.16 15 m/s turbulent wind condition

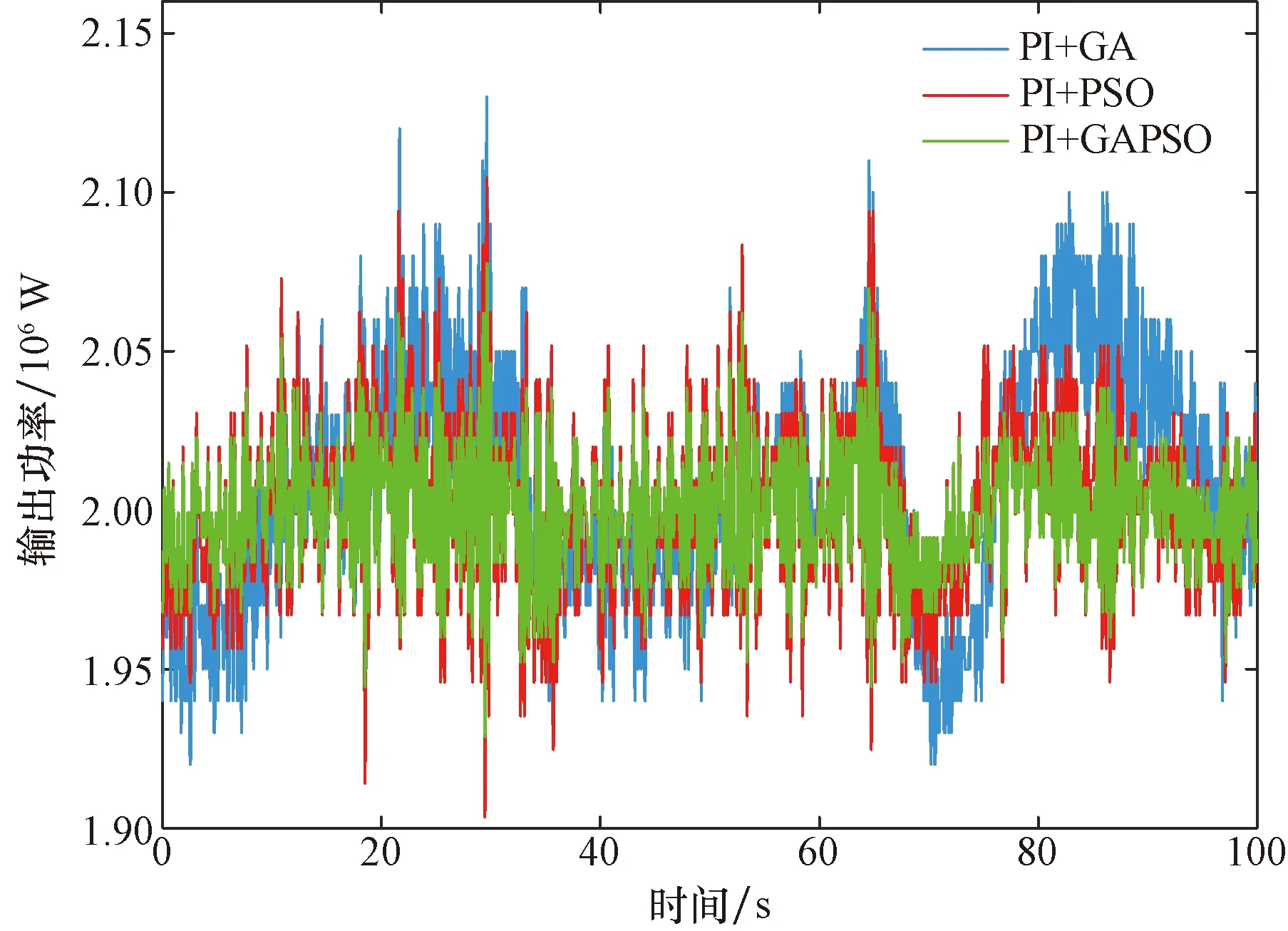
图17 输出功率比较Fig.17 Comparison of output power

图18 发电机转速比较Fig.18 Comparison of generator speed

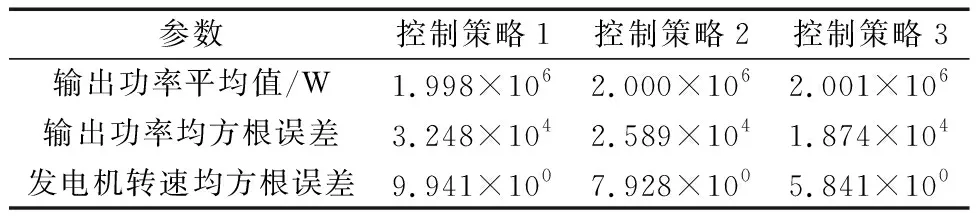
表8 控制精度比较Table 8 Comparison of control accuracy

与控制策略1相比,控制策略3输出功率平均值达到额定功率,其均方根误差降低42.30%。同时,发电机转速均方根误差降低41.24%。与控制策略2相比,控制策略3输出功率平均值达到额定功率,其均方根误差降低27.62%。同时,发电机转速均方根误差降低26.32%。上述结果显示:GAPSO相较于GA和PSO优化变桨系统PI控制参数能够保证输出功率达到额定功率的同时平抑输出功率和发电机转速的波动。

4.2.2 叶片根部载荷分析

在变桨控制中由于频繁改变桨距角将导致叶片根部载荷加剧。桨距角的控制效果如图19所示。由图19分析得到的性能指标情况如表9所示。

与控制策略1相比,控制策略3桨距角均方根误差降低7.84%。与控制策略2相比,控制策略3桨距角均方根误差降低4.08%。上述结果显示:GAPSO相较于GA和PSO优化变桨系统PI控制参数可以抑制桨距角的频繁波动。

叶片根部摆振弯矩(Mx)和挥舞弯矩(My)的控制效果是衡量叶片根部载荷的指标。时序载荷Mx和My如图20、图21所示。分析图20、图21得到的性能指标情况如表10所示。

为进一步评价叶片根部的载荷情况,采用损伤等效载荷(damage equivalent load, DEL)将时序载荷用量化,如表11所示。

与控制策略1相比,控制策略3叶片根部时序载荷Mx的极差、平均值分别降低57.25%、16.39%,并且叶片根部Mx的DEL降低10.87%。叶片根部时序载荷My的极差、平均值分别降低32.08%、13.33%,并且叶片根部My的DEL降低7.74%。与控制策略2相比,控制策略3叶片根部时序载荷Mx的极差、平均值分别降低37.08%、6.71%,并且叶片根部Mx的DEL降低5.38%。叶片根部时序载荷My的极差、平均值分别降低10.65%、4.88%,并且叶片根部My的DEL降低3.86%。上述结果显示:GAPSO相较于GA和PSO优化变桨系统PI控制参数能够显著降低叶片根部载荷情况。