基于共旋坐标法的空间桁架几何非线性分析

2023-12-08朱丽君颜海泉董正方

科学技术与工程 2023年31期

朱丽君, 颜海泉, 董正方*

(1.河南大学土木建筑学院, 开封 475004; 2.上海市政工程设计研究总院(集团)有限公司, 上海 200082)

传统的几何非线性分析方法完全拉格朗日列式法(total Lagrange formulation, TL)与更新拉格朗日列式法(updated Lagrange formulation, UL)均未考虑变形后的坐标系的变化[1],单元发生较大刚体转动时的计算误差较大。共旋坐标法基于UL法,通过建立随动坐标系[2-4]来解决这一问题,单元刚体转角任意大时计算都是精确的;共旋坐标法迭代过程中,整体坐标系与局部坐标系的转换矩阵不断更新,几何非线性通过坐标转换计算而被考虑进来;目前诸多工程实例中均需考虑几何非线性与材料非线性的耦合作用[5-6],相较于TL法和UL法,共旋坐标法可使耦合非线性问题的刚度矩阵脱耦、计算更加简洁[7],在大位移小应变几何非线性分析中更具有优势。

共旋坐标法[8]的基本原理是将单元刚体位移扣除,从而得到单元纯变形与杆端力的关系,因其高效精确的优点而被广泛应用于梁杆单元的几何非线性分析中。常用的共旋坐标法有随动坐标系法[7,9]与随转坐标系法[10]两种:前者提出以单元i节点为原点建立随动坐标系,将梁杆的大位移分解为随动坐标的刚性位移与弹性位移;后者将随动坐标系的原点设在初始局部坐标系原点处,此坐标系随单元转动而不平动,进而得到几何非线性与线性平衡方程的统一表达式。蔡松柏等[11]、邓继华等[12]、冯晓东等[13]利用桁架单元的几何与物理关系,通过变分法直接推导出桁架单元的刚度矩阵,进一步简化了桁架几何非线性的计算,并编制基于面向过程技术的程序或对其二次开发。马玉全[14]对传统共旋坐标法中的单元长度、荷载及抗力进行改进,使其更好地适用于梁杆单元,提高了计算精度,并编制相关程序。李东升等[15]使用逆向运动法将梁单元的刚体旋转分解,从而计算出精确的旋转矩阵,并编制了相应有限元程序。

但共旋坐标法的随动与整体坐标系的转换矩阵需以整体与初始局部坐标系的转换矩阵为中介矩阵[9-10,14,16],若能进一步简化转换矩阵的计算,将会减少软件中矩阵的存储步骤,尤其对于大型算例,计算效率将显著提高。且共旋坐标法在程序中的实现诸多基于面向过程技术[11,14,17],然而面向对象技术具有更高的数据抽象和封装能力,更易实现程序功能的扩充,也是有限元程序设计的主流工具[18]。此外,桁架几何非线性的判断条件还缺乏研究,经验理论认为应变达到5%时考虑几何非线性,但此理论在桁架中的适用性有待验证。

现通过取整体坐标系原点为随动坐标系的原点,得到更简单高效的转换矩阵计算方法,使用面向对象C++语言在程序Aduts中实现此法桁架单元。在程序中进行算例分析并与理论解对比来验证其正确性,并对其进行参数分析,总结桁架几何非线性的判断依据。

1 桁架单元共旋坐标法理论

常用桁架单元的共旋坐标法主要有以单元端点、初始局部坐标系原点为随动坐标系的原点两种[7-8],且多基于平面问题。

1.1 随动坐标系法

此理论需用到三个坐标系:整体坐标系、初始局部坐标系、随动坐标系,随动坐标系的原点为单元的i节点,此坐标系随单元平动和转动,以平面问题为例。

首先需计算整体坐标系与初始局部坐标系的转换矩阵R0,计算式为

(1)

式(1)中:lxX、lxY为局部坐标系的x轴对整体坐标系X、Y轴的方向余弦;lyX、lyY为局部坐标系的y轴对整体坐标系X、Y轴的方向余弦。

再计算初始时刻局部坐标系与t时刻局部坐标系的转换矩阵Rt,计算式为

(2)

式(2)中:α为初始局部坐标系x轴与t时刻局部坐标系的夹角(图1),计算式为

(3)

最后计算整体坐标系与t时刻局部坐标系的转换矩阵R=Rt×R0。

XOY为整体坐标系;xoy为初始局部坐标系;xtotyt为随动坐标系; i0、j0表示初始时刻单元的两个端点位置;it、jt表示t时刻后单元的两个端点位置图1 单元位形及随动坐标系Fig.1 Configuration of element and concomitant coordinate system

1.2 随转坐标系法

如图2所示,XOY为整体坐标系,xoy为初始局部坐标系,xtotyt为随动坐标系,以平面问题为例,此理论与随动坐标系法的计算步骤相同,只是初始局部坐标系与随动坐标系的原点重合,随动坐标系相对于初始局部坐标系只转动,但各转换矩阵的计算列式与1.1节中一致。

由此可见,这两种建立随动坐标系的方法都会使随动与整体坐标的转换矩阵R的计算分成三步:①计算整体与初始局部坐标系的转换矩阵R0;②计算随动与初始局部坐标系的转换矩阵Rt;③整体与随动坐标系的转换矩阵R=Rt×R0。

桁架共旋坐标法的核心为转换矩阵的更新,而转换矩阵在每个迭代步都需根据位移值来同步更新,若是能对转换矩阵的计算做进一步的简化,几何非线性的计算将更加高效,尤其是对于大型工程,将会有效节省计算时间。

图2 单元位形及随转坐标系Fig.2 Configuration of element and co-rotational coordinate system

1.3 基于整体坐标系的随转坐标系法

在对空间桁架进行大变形几何非线性分析时,将随动坐标系的原点设在整体坐标系原点处,此随动坐标系只随单元发生转动而不平动。

如图3所示,将t时刻的单元平移,使单元的i节点与整体坐标系的原点重合,单元两节点的连线方向为随动坐标系xt轴方向,且假设整体坐标系的Z轴始终在随动坐标系的xtotzt面内,xt轴的方向向量由单元与整体坐标系三个坐标轴的夹角即可计算出,yt轴的方向向量可由xt的方向向量与xtotzt面

图3 空间桁架坐标系与位形Fig.3 Coordinate system and configuration of space truss

内且与xt轴不重合的向量(0,0,1)叉乘求得,zt轴的方向向量可由yt轴与xt轴的方向向量叉乘得到。

图3中,α、β、γ分别为变形后的单元与整体坐标系X、Y、Z轴的夹角,也即随动坐标系x轴与整体坐标系夹角,平面P1与xt轴垂直,平面P2与整体坐标系Z轴垂直,平面P1与P2的交线即为随动坐标系yt轴的方向,zt轴方向由右手定则确定。

现做以下假设:(Xi,Yi,Zi)、(Xj,Yj,Zj)分别为变形前单元i、j端的坐标;(Xi+Ui,Yi+Vi,Zi+Wi)、(Xj+Uj,Yj+Vj,Zj+Wj)分别为变形后单元i、j端的坐标;Uλ,Vλ,Wλ(λ=i,j)为单元i、j端沿X、Y、Z轴方向的位移值;L0、Lt分别为变形前后的单元长度。则xt轴的三个方向余弦值为

cosα=(Xj-Xi+Uj-Ui)/Lt

(4)

cosβ=(Yj-Yi+Vj-Vi)/Lt

(5)

cosγ=(Zj-Zi+Wj-Wi)/Lt

(6)

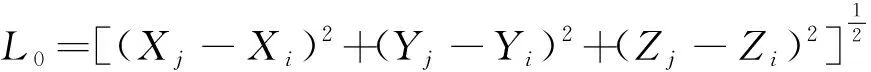
(7)

Lt=[(Uj-Ui+Xj-Xi)2+

(Vj-Vi+Yj-Yi)2+

(8)

则随动坐标系xt轴的方向向量为(cosα,cosβ,cosγ),yt轴的方向向量为(-cosβ,cosα,0),zt轴的方向向量为(-cosαcosγ,-cosβcosγ,cos2α+cos2β)由yt、xt两坐标轴的方向向量叉乘得来。

则可得到随动坐标系与整体坐标系的转换矩阵R[19]。即

(9)

由局部坐标系下杆端轴力计算式(10)及式(4)～式(6),可得轴力在整体坐标系六个方向上的分力,再经变分运算可得单元刚度矩阵K=KL+KN,其中KL为刚度矩阵的线性部分,KN为刚度矩阵的非线性部分,也称几何刚度矩阵。表达式为

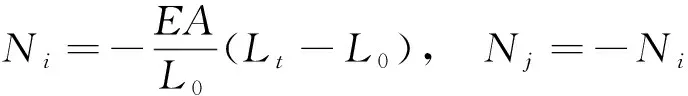
(10)

式(10)中:E为杆件的弹性模量;A为其截面面积。

[KL]6×6=RTTlbTK3×3TlbR

(11)

(12)

(13)

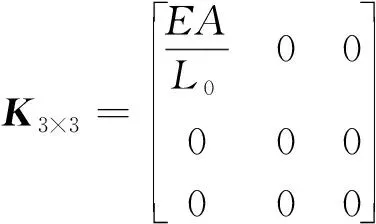
(14)

(15)

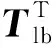
整体坐标系下刚度矩阵的具体表达式为

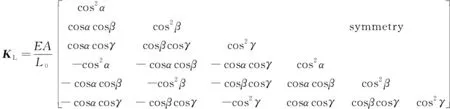
(16)

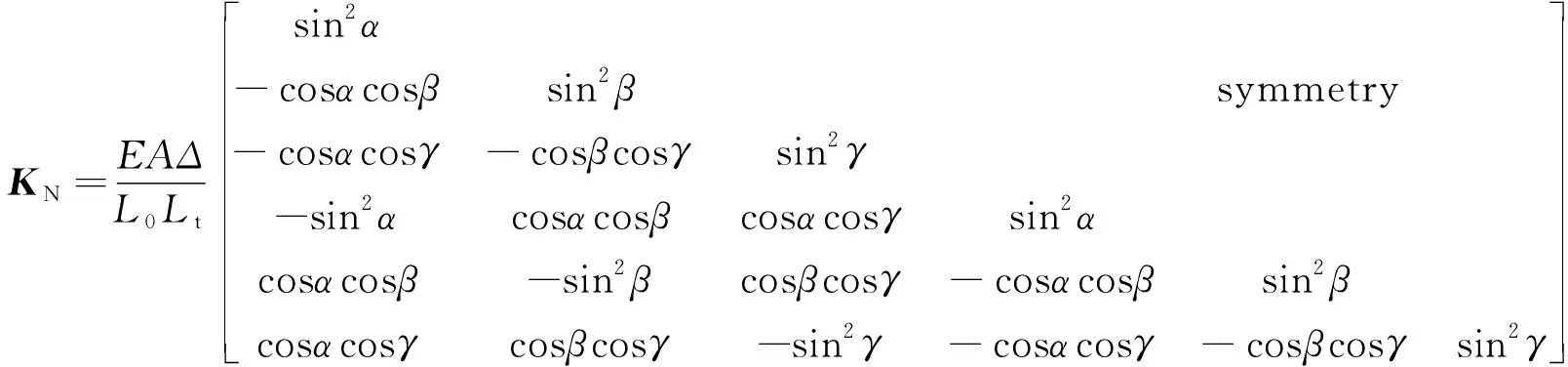
(17)

式中:Δ为杆件单元长度变化,Δ=Lt-L0; symmetry表示关于对角线对称的矩阵的另一部分。

(18)

将随动坐标系原点取为整体坐标系原点的优点是可直接得出转换矩阵,不需整体坐标系与初始局部坐标系的转换矩阵做中介,减少了计算步骤,提高了计算效率。

2 共旋坐标法桁架单元的程序实现

2.1 单元接口基类

以桁架的共旋坐标法为原理,使用面向对象C++语言在程序Aduts中编写了桁架单元。面向对象语言由于具有动态内存分配的功能,程序的数据组织相互独立,修改某一处的数据不会对其他部分数据造成影响,使程序更易扩充;且面向对象技术中的数据类型可自行定义,不会像面向过程技术一样受数据类型的限制,故更易编制类型丰富的单元及本构材料;面向对象程序设计方法将程序框架划分为不同的类,每个类只进行抽象描述,具体的定义在各子类中实现,使用时不需知道子类的实现细节,具有很好的数据封装与代码可重用性,易于程序开发。

本文程序中抽象出了单元接口基类ElementInterface.h,开发人员通过重写其内部的虚函数来添加所需要的单元子类。接口定义了继承该接口的子类需要实现的方法,其虚函数如表1所示。

本程序的单元接口基类Topology2()函数中设置了附加参数,各单元子类可根据功能需求自行添加与修改附加参数,而不会对其他单元子类产生影响,这也是本程序的一大优点,附加参数的设置简化了单元子类的开发、维护了程序的封装性与多态性。

表1 ElementInterface类中的虚函数Table 1 Virtual functions of ElementInterface

2.2 桁架单元的扩展

通过继承单元接口基类的虚函数实现桁架单元的扩展,关键步骤为每个迭代步对单元转换矩阵、刚度矩阵、抗力向量的更新,这就需处理好程序框架对单元子类中各函数的调用工作。故Aduts程序中桁架单元的编写工作分为两部分,一是对单元接口基类中函数的具体定义,二是在不修改程序框架的前提下,完成对单元子类中各函数的调用,从而实现各数据的更新与计算流程。

在重写基类函数Topology1()时,因所加桁架单元是考虑几何非线性的,故几何非线性标签改为true。重写函数Topology2()时,附加参数有四个:“length0”“Initial”“lengthT”与“CorotTag”,分别表示桁架单元的初始单元长度、调用转换矩阵标签(用于判断是进行迭代前转换矩阵的调用,还是进入迭代步后转换矩阵的调用)、t时刻的单元长度与共旋坐标法的标签(用于判断是否使用共旋坐标法),比普通单元(不考虑几何非线性的单元)多了后三个附加参数。

重写转换矩阵ComputeTransformMatrixData()时,与普通单元不同的是,共旋坐标法桁架单元需随着单元位移的更新而更新局部坐标系与整体坐标系的转换矩阵,普通单元只需根据初始位形计算一次转换矩阵。

重写刚度矩阵ComputeElementStiffMatrix()时,由于几何非线性单元的刚度矩阵分为线性刚度与非线性几何刚度两部分,故比普通单元多了几何刚度矩阵的定义部分。

其余单元接口基类函数的重写与普通单元基本相同。

实现单元子类中各函数的准确调用是单元扩展的难点之一,本文中对共旋坐标法桁架单元计算流程的处理如图4所示。

图4 桁架的计算流程Fig.4 Calculational flow of truss

图4中计算流程与普通单元的区别在于转换矩阵的更新,这需通过在单元子类内部定义附加参数来实现。不使用共旋坐标法的单元只在迭代之前计算一次整体坐标与局部坐标系的转换矩阵,使用此法时则在每个迭代步都需更新转换矩阵。由此可见,通过在单元子类中设置不同附加参数,满足了单元子类特殊的功能需求,对单元子类的扩展有重要作用。

3 算例

3.1 单元正确性的验证

如图5所示桁架,各杆件的弹性模量与横截面积大小一致,图5中桁架单元桁架跨长a=100 cm,b=-2 cm,弹性模量E=200 GPa,横截面积A=4 cm2,桁架顶端作用竖直向下的集中荷载,划分10个荷载步,位移收敛条件为|ΔU/U|≤1×10-3。

本文程序的拱顶位移计算结果与理论结果[20]的对比如图6所示,由图6可知,本文程序解与理论值吻合度很高,验证了本文程序中桁架单元的正确性。

图5 计算结构模型Fig.5 Structural model of calculation

图6 拱顶竖向位移对比Fig.6 Vertical displacement comparison of vault

3.2 参数分析

由应变与轴力的公式可知,应变大小与拱跨比b/a、P/EA的值紧密相关,无论单元长度、截面面积如何变化,只要b/a与P/EA的值不变,应变值不会改变。

因此,对桁架进行几何非线性分析时,通过改变图5中桁架的拱跨比b/a与P/EA的值,使应变保持在指定值,得到图7中几何非线性与线性位移误差与拱跨比关系图。位移相对误差为线性与几何非线性位移之差与非线性位移的比值,其中,几何非线性计算的第一次结果即为线性结果,此参数分析得出的结论对任意长桁架均适用。

位移误差是线性计算未考虑单元的位形变化、将刚体转动计入到线性应变中,使得线性位移的计算结果出错而引起的。

如图7所示,当应变分别为1%、2%、3%、4%、5%、8%,拱跨比分别为0.073、0.103、0.125、0.144、0.161、0.201时,位移相对误差等于工程精度误差要求5%;各应变值对应的拱跨比分别为0.081、0.115、0.140、0.161、0.179、0.220时几何非线性与线性的相对误差为0;各应变值对应的拱跨比分别为0.093、0.130、0.159、0.182、0.202、0.251时几何非线性与线性的相对误差为-5%。

由图7可知,应变不变,拱跨比越小位移的相对误差越大,故即使应变未超过5%,位移误差可能会超过工程精度误差要求,也需考虑几何非线性。因此,判断桁架是否考虑几何非线性时,应将桁架的应变与拱跨比的具体数值结合来讨论,不能单纯以应变的大小作为判断标准。