基于虚拟电阻的复杂直流网络P-V下垂控制方法

王辞喻, 赵兴勇

(山西大学电力与建筑学院, 太原 030031)

随着化石能源的枯竭和环境污染问题的日益凸显,以风、光为主的可再生能源分布式发电受到社会各界的广泛重视。为应对分布式能源随机性、间隙性等特性,解决其可靠接入的问题,微电网作为解决方案被提出[1]。

为了保证微电网的稳定运行,需要制定一套有效的控制管理策略,以满足不同的系统要求。文献[2]提出了一种用于低惯量系统的多端柔性直流输电(voltage source converter based on multi-terminal direct current,VSC-MTDC)系统的协调控制策略,但面对大扰动时,该方法精度较差。文献[3]对VSC-MTDC系统发生大扰动时会造成频率变化的问题进行优化,在换流器控制系统中加入功率-频率(P-f)下垂控制,但没有考虑线路阻抗的因素。文献[4-5]分别提出基于线路阻抗不一致影响下的微电网功率分配控制策略,实现了系统功率的精确分配。文献[6]针对低压微电网下并联逆变器在容量比和线路阻抗比不一致的条件下无法实现功率合理输出的问题,结合传统下垂方法提出了一种改进的控制策略。同时,多电平换流器多端柔性直流输电(modular multilevel converter multi-terminal direct current transmission, MMC-MTDC)系统中,其电压质量容易受功率波动影响、直流电压偏差较大,不利于系统的安全稳定运行。 针对这一问题,文献[7]提出了一种不平衡功率可调节范围的量化分析方法。

与此同时,直流微电网不存在交流微电网中的频率、无功、相位等问题,具有控制简单、线路损耗低、系统成本低、可靠性高等优势,因此更多人把目光放在了直流微电网的研究[8]。文献[9]提出一种基于下垂曲线截距调整的直流微电网自适应虚拟惯性控制(adaptive virtual inertia control,AVIC)方法,然而其对并联运行时的系统功率均分准确度较差。对此,文献[10]提出了一种基于改进动态下垂控制的微电网控制方法,用于提高分布式电源并联运行时的系统功率均分准确度以及负荷变化时的系统稳定性。此外,文献[11]提出一种考虑线路电阻影响的自适应下垂控制。但在传统电压-电流(V-I)型下垂控制中,会存在输出电流分配不均和母线电压不稳定的问题。针对该问题,文献[12]提出一种带有电压补偿的改进I-V型下垂控制策略。对于传统下垂控制,可改进的地方还有很多。例如文献[13]基于微网逆变器输出功率解耦的研究取得成果,提高了下垂控制的功率分配精度和系统的稳定性。文献[14]提出基于虚拟阻抗和模糊比例-积分-微分(proportional integral differential,PID) 的低压微电网下垂控制策略,用于解决在低压微电网中负荷发生波动时,P-V/Q-f(Q为无功功率)下垂控制对功率分配、系统电压和频率同时进行控制的精准度就会下降的问题。

除了对传统下垂控制的本身进行改进,研究人员同样对控制回路之外的各个方面进行优化。文献[15]提出了一种用于减小电流传感器数量的改进下垂控制方法,进一步提高了下垂控制的经济性,但其功率分配精度略有下滑。文献[16]提出双重下垂控制,该算法采用两级下垂控制,改进后的一级下垂控制用于补偿线路阻抗造成的功率偏差,实现直流母线电压稳定;二级下垂控制实现同类型储能单元间的功率分配。但该方法对通信网络的要求过高。为了降低系统运行对通信网络的依赖,文献[17]提出一种计及效率特性的直流微网经济下垂控制策略。针对环流问题,文献[18]引入了纯感性的虚拟阻抗,在减小功率耦合的同时提高了环流抑制效果,同时针对虚拟阻抗的使用而导致的母线电压跌落,在无功下垂控制回路中使用了电压补偿,减小电压跌落的同时得到了更加精准的输出电流。

但上述方法的研究都是基于简单系统的下垂控制优化,文献[19]提出一种基于自律分散控制的网孔型直流电网下垂系数计算方法,但其忽略了对特殊节点的处理,当某个节点及其附近的节点的接入电压明显高于或弱于均值时便无法处理。文献[20]提出了一种复杂直流电网下垂系数的计算方法,但其针对的对象是高电压等级的电网,在高压下忽略了部分阻抗对控制系统的影响。上述对中小复杂直流电网的研究较少,且大多是在放射状结构的基础上进行分析和处理,对于环网式直流微电网和群网式直流微电网等复杂微电网尚未有较好的处理方法。

综上,现提出一种对中小型直流复杂电网的等效方法,将复杂拓扑结构等效为放射状拓扑结构。首先,定义虚拟母线并将各个节点的平均值及中位数值之和的一半定义为虚拟电压值,再将直流母线与直流系统中电压值相等的点相连,这些点为虚拟节点。按虚拟节点在不同支路中的存在情况将系统节点分为3类节点并分别进行处理,得到一个等效放射状直流电网拓扑结构。随后,根据化解结果进行公式代换得到P-V下垂控制的系数公式。最后在MATLAB/Simulink中搭建了4端直流电网仿真模型,对基于虚拟电阻的P-V下垂控制策略的各项数据进行仿真验证。上述研究可以大幅度简化一般性复杂网络的下垂系数求取复杂度及减少大量的运算次数。

1 复杂系统的优化方法

假设直流系统稳定,复杂直流系统的优化方法分为三步,首先确定虚拟母线电压值,然后对节点进行分类并处理,最后得出等效拓扑图。

1.1 虚拟母线电压

虚拟母线电压值V*定义为:各节点电压值的平均值Vave和中位数Vmid之和的一半。该定义可有效减少第三类节点的数量,降低运算难度。

(1)

系统中与虚拟母线电压值相等的点定义为虚拟节点,同时根据支路中包含虚拟节点的情况将系统节点分为以下3类节点。

1.2 第一类节点

以自身为中心散出去的支路中全部含有虚拟节点的节点为第一类节点。其等效电阻为

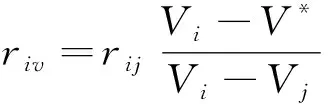
(2)

(3)

式中:ri,v为节点i到虚拟节点的电阻;rij为节点i到节点j的电阻;Vi和Vj分别为节点i与节点j的节点电压;ri为节点i到虚拟母线的等效电阻。

第一类节点的等效本质为:节点与虚拟母线的并联,如图1所示。

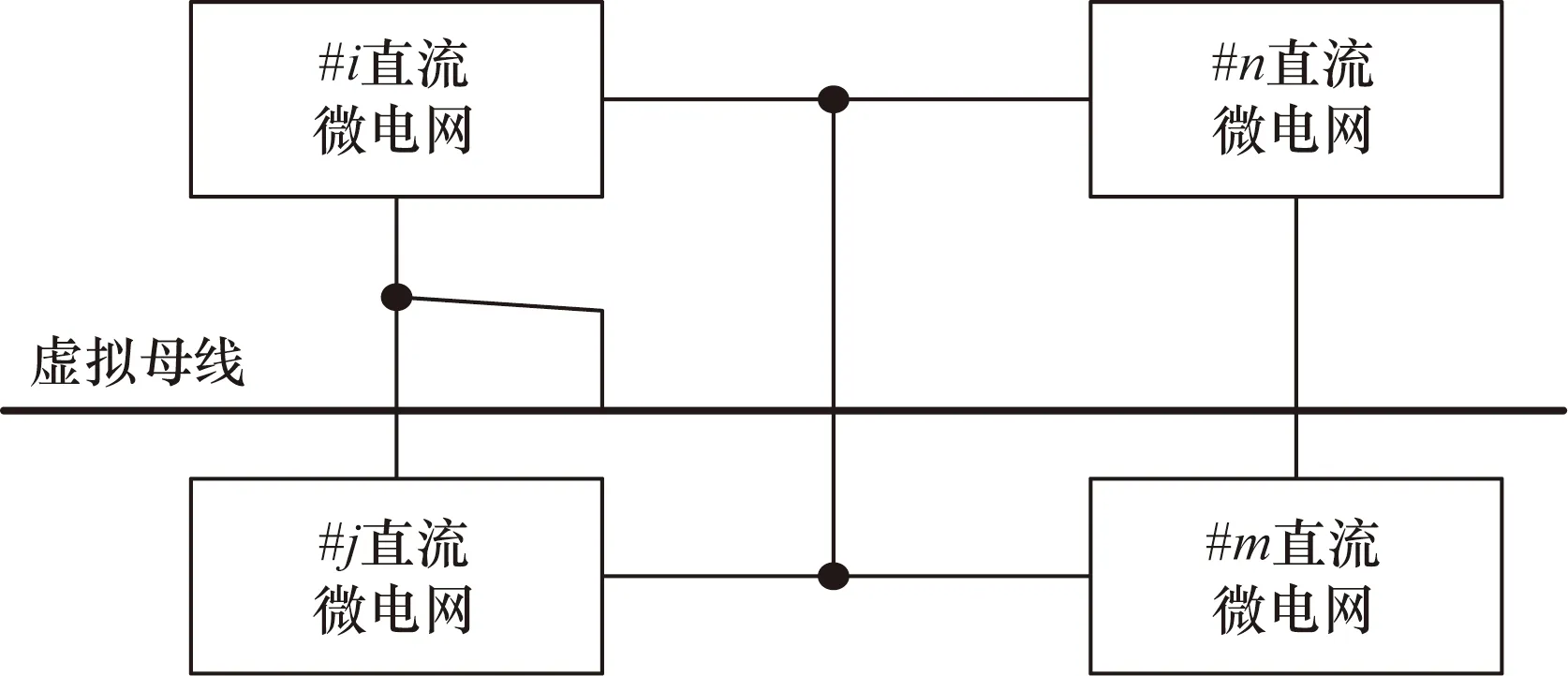
图1 第一类节点Fig.1 The first type of node

1.3 第二类节点

以该节点为中心散出去的支路,部分有虚拟节点,另一部分无虚拟节点的节点为第二类节点。如图1中的m节点和n节点。根据基尔霍夫定律总结当前电路节点的电流电压关系,然后根据对外等效的原则对目标数值进行推算。第二类节点的电路等效图如图2所示,存在如下关系:

(4)

式(4)中:Ii、Ij、Iv分别为i节点、j节点、虚拟节点的电流;Vi、Vj、V*分别为i节点、j节点、虚拟节点的电压;rvi、Ivi为i节点与虚拟节点之间的虚拟电阻值及电流值;rij、Iij为i节点与j节点之间的电阻值及电流值;rvj、Ivj为j节点与虚拟节点之间的虚拟电阻值及电流值;r′vi、I′vi为等效转换后节点i与虚拟节点的等效虚拟电阻及电流;r′vj、I′vj为等效转换后节点j与虚拟节点的等效虚拟电阻及电流。

图2 第二类节点Fig.2 The second type of node

经过等效代换,可得

(5)

(6)

如此,便可根据式(5)或式(6)得到该节点到虚拟节点的等效虚拟电阻。

1.4 第三类节点

以该节点为中心散出去的所有支路,不存在任何虚拟节点的节点为第三类节点。第三类节点的电路等效图如图3所示,存在如下关系:

(7)

经过等效代换,可得

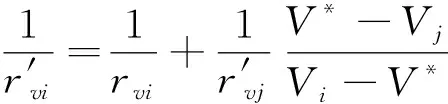
(8)

图3 第三类节点Fig.3 The third type of node

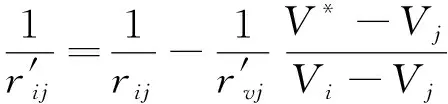
(9)

如此,便将第三类节点化归为第二类节点。

需要说明的是,在处理的过程中缺少一个元r′vj,但r′vj对最终结果不产生任何影响,只是一个过程值,因此可以设定一个值来简化运算。

2 P-V下垂控制策略及参数的求取法

2.1 P-V下垂控制策略在VSC中的应用

目前广泛使用的控制回路主要有矢量电流控制(vector current control, VCC),虚拟同步机控制(virtual synchronous generator control,VSG)两种。直流微电网下垂控制的普遍实现方式是:将下垂曲线控制加在变换器的电压电流双闭环控制之外,作为控制外环,得到变换器输出直流电压参考值[1]。

根据相应的公式求得下垂系数之后,将其添加进外环控制回路中,将功率-电压(P-V)下垂曲线的控制和外环控制相结合,得到参考电流的d轴分量,并通过后续的内环控制完成对整个系统的控制。其中下垂控制的原理如图4所示。

如图4所示的VSC(voltage source converter)控制中的外环控制,参数Vref、Pref分别是直流侧电压和功率的参考值,V、P是变换器直流侧的实际输出电压及功率。

图4 P-V下垂系数的应用Fig.4 Application of P-V droop coefficient

2.2 下垂系数的求取

经过以上的处理,将系统等效为简单的放射式拓扑网络,并将等效模型给出,进行P-V下垂参数的求取。如图5所示为直流系统当前状态和目标状态的等效模型。

由图5可知有以下关系:

(10)

同时,传统I-V下垂和P-V下垂的表达式分别为

Iref-I=Kc(Vref-V)

(11)

V0、V*分别为变换器电压、虚拟母线电压;r为变换器的虚拟电阻;rc为当前状态的虚拟线路电阻;r0为额定状态的虚拟线路阻抗;V、I为当前状态的变换器输出电压、电流;Vref、Iref为额定状态 的变换器输出电压、电流图5 变换器当前状态和目标状态的等效模型Fig.5 Equivalent model of the current state and target state of the converter

Pref-P=Kv(Vref-V)

(12)

式中:Kc、Kv分别为传统下垂系数和P-V下垂系数。

在式(11)两端各乘一个V0,并改写为

(13)

易知有如下关系:

(14)

综上所述,将公式进行整理后,可知下垂系数Kv计算公式为

(15)

该下垂系数的求取公式及控制方法适用于复杂度不高的中小型电力网络,及电压等级35 kV以下的中低压配电网。

3 仿真验证

在MATLAB/Simulink环境中搭建了4端仿真系统,其拓扑图如图6所示,参数值如表1所示。

图6 4端环形直流系统Fig.6 4-terminal ring DC system

其中VSC1在开始时采用固定功率控制,后转为下垂控制;VSC2在开始时采用固定电压控制,后转为下垂控制;VSC3采用固定电压控制;微源4采用V-f控制,同时作为扰动源,在1.2～1.7 s产生一个大小为450 kW的功率阶跃。

节点1和节点2在系统稳定后,将控制方式转变为传统下垂控制和基于虚拟阻抗的P-V下垂控制,其中后者在之后简写为P-V下垂控制。为了对比控制效果,各换流站采用不同的初始控制方式,具体的控制方式及参考值见表1。

表1 换流站初始控制方式Table 1 Initial control mode of converter station

根据仿真可知,4个节点的入网电压依次分别为4.943、4.982、4.996、4.896 kV,根据式(1)得虚拟母线电压约为4 958.375 V。由此可知,在节点1与节点2及节点3与节点4的支路上存在虚拟节点,故4个节点均属于第2类节点。仿真中各项系统参数详情见表2。传统下垂控制与本文所提出的P-V下垂控制的电压变化如图7所示。

由图7可知,两种下垂控制在扰动发生时,对自身节点均产生了不同程度的控制效果。发生扰动时节点1的电压的扰动幅度控制效果很好,P-V下垂为83 V,相比传统下垂的127 V较小,同时在扰动结束后的电压恢复时间上,前者为0.12 s,相较后者的0.16 s小。节点2的初始控制采用与节点1不同的固定电压控制,在转变为下垂控制后,控制效果也略有不同,在幅值上的表现也优于节点1,但时间控制上无明显区别。节点2的扰动幅值和恢复时间,传统下垂控制是85 V和0.16 s;P-V下垂控制为44 V和0.15 s。可见,在电压控制上,P-V下垂控制相较传统下垂控制在控制性能对比上略有优势。

表2 仿真系统各项数值Table 2 The values of the simulation system

传统下垂控制与本文所提出的P-V下垂控制的功率变化如图8所示,控制性能对比情况如表3所示。

由图8所示可知,两种控制方式在功率控制性能的对比上较为相近,但仍有区别。在扰动发生时,节点1的两种控制方式的功率变动非常接近,幅值都为0.17 MW,且恢复时间都为0.15 s。节点2的情况也较为接近,传统下垂的扰动幅值为0.06 MW,恢复时间为0.16 s;P-V下垂的两项数值为0.05 MW及0.14 s。

综上所述,在负荷侧发生大规模功率扰动时,基于复杂网络等效基础上的两种控制方法均产生了不错的控制效果。但在电压偏移幅值、电压恢复时间、功率波动幅值、功率恢复时间等控制性能的对比上P-V下垂控制要略优于传统下垂控制。该仿真结果也从正面验证了复杂网络的等效方法的可行性,及基于其推导出的P-V下垂控制的有效性。

表3 控制性能对比情况Table 3 Control performance comparison situation

4 结论

本文设计了一种复杂电网的等效方法,并基于其等效结果提出一种基于虚拟电阻的P-V下垂控制方法。通过对负荷侧大规模功率扰动的仿真结果研究,得出如下结论。

(1)在直流电压偏差、功率波动幅值等幅值控制的性能对比上,虚拟阻抗P-V下垂控制具有很好的效果,能有效抑制负载变化导致的电压偏移及功率波动。

(2)在电压恢复速度、功率恢复速度等恢复速度控制的性能对比上,虚拟阻抗P-V控制对比传统下垂控制并无明显优势,但在部分情景下恢复速度较快。

(3)本方法不需要电流测量环节,减少了部分电流传感器的数量,经济上也具有一定的优势。