一种基于CNN和RF的恒星大气参数测量方法

王莉莉, 屠良平, 李双川

(辽宁科技大学理学院, 鞍山 114051)

郭守敬望远镜(large sky area multi-object fiber spectroscopy telescope)是大天区面积多目标光纤光谱巡天望远镜,于2012年9月启动之后,光谱数据量急速增加,目前最新释放的LAMOST-DR9的数量已超过千万量级。面对如此庞大的光谱数据量,如何精准预测光谱的科学参数成为天文光谱学分析的研究热点之一[1]。恒星大气参数主要包括有效温度、表面重力、金属丰度和微观湍流速度,这些参数不仅是造成恒星光谱差异的原因也是参数测量的主要内容。目前,参数测量常用的机器学习算法包括支持向量回归[2]、贝叶斯回归[3]和随机森林[4]等被用于恒星大气参数预测,但这些机器学习算法在面对大量高维、强相关性及高冗余的恒星光谱数据时会存在一定的局限性。由于恒星在参数空间中分布广泛,不同的光谱特征对大气参数具有不同的敏感性,因此很难依靠单一的方法来推导具有高精度的恒星大气参数。

近年来,有研究者使用多种算法结合的方法进行恒星大气参数测量。Xiang等[5]开发的LAMOST恒星参数管道,基于模板匹配技术从LAMOST光谱中确定恒星参数(径向基速度、有效温度、表面重力和金属丰度),实验结果表明基于模板匹配技术得到的参数精度较高。Lu等[6]使用最小绝对收缩和选择算子(least absolute shrinkage and selection operator,LASSO)算法,选择部分候选特征作为光谱特征,估算恒星大气参数。Yang等[7]提出了一种利用自动编码器提取恒星光谱的代表性特征,通过反向传播网络估计恒星大气参数,结果表明该方案在估计恒星大气参数方面具有良好的性能。

深度学习作为目前流行的算法之一,也逐渐应用在恒星大气参数测量中,潘儒扬等[8]基于深度学习理论,提出深度学习在恒星大气参数测量方面的应用,提出了一个5层栈式自编码深度神经网络,对恒星大气参数进行自动估计,结果表明栈式自编码深度神经网络精度较好。邓诗语等[9]利用可变形卷积神经网络(deformable convolutional network,DCN)方法对恒星大气参数进行分析,验证了DCN算法在参数测量上效果的优越性。这些方法更多考虑的是光谱数据的物理特征与科学参数之间的关联,但深度学习在研究恒星大气参数测量这一方面的内容相对较少,另外在面对精度差,测量时间长以及深度学习不能直接进行一维光谱参数测量等问题亟待解决。因此,现通过将一维光谱变成二维的形式,充分利用卷积神经网络对图像优秀的特征提取能力进行参数测量。它通过提取光谱数据中更高层次的非显性参数特征,进而达到提高精度的目的。

1 CNN方法和RF方法

1.1 CNN网络模型

卷积神经网络(convolutional neural network)主要由输入层、卷积层、池化层、全连接层和输出层5个部分构成[10],如图1所示。但并未用到完整的结构网络,只是利用了CNN的卷积和池化层对图像优秀的特征提取能力。

卷积层通过卷积核按照特定的步长在输入矩阵上滑动,直到遍历整个区域的特征后得到输出矩阵,该过程可以用数学模型描述为

(1)

池化层设置在卷积层之后,可以通过向下采样压缩输入而不影响输入质量[11],降低特征维度。CNN选择最大池化方法对特征进行降维处理,在卷积层和池化层之间设置BN(batch normalization)层,BN层可以解决因数据分布的变化需要调节权重而导致的训练速度减慢的问题,它会将上层输出的数据特征进行批归一化再输出,以获取更加集中有效的特征信息。

1.2 随机森林回归模型分析

随机森林(random forest, RF)是Breiman[12]提出的一种基于决策树组合的可用于分类、回归以及多维数据处理的机器学习算法,不仅能够平衡样本中分布不均匀数据的误差,而且对异常值和噪声有很好的容忍度[13]。RF不仅可以处理大型多维数据,而且适用于非线性问题。更重要的是,RF对每一棵树都使用了自助抽样技术。相对于单颗决策树,RF方法可以在自助采样后对每棵决策树进行单独训练并生成平均结果,从而减少了过拟合问题。因此RF算法具有预测效率好和可解释性等诸多优点。更重要的是RF算法并不需要过多的调参,得到的精度较高。鉴于此特点,现选择RF算法作为恒星大气参数测量的回归器,其组成如图2所示。

2 模型架构与参数

考虑到机器学习出现的弊端以及深度学习在图像特征提取方面的优势,现设计一种CNN和RF的组合算法对恒星大气参数进行测量,简记为CNN-RF,如图3所示。CNN通过卷积和池化不断的进行交替操作,恒星光谱数据中的隐含特征得以被提取,然后基于恒星光谱数据产生的特征图进行压平(Flatten)作为下一个算法的输入。卷积池化之后,在特征输出节点间设置展平层,将提取到的光谱特征输入到RF特征筛选层,通过特征重要性计算,过滤掉无用特征,剩余特征作为RF的输入向量。最后将提取好的特征展平输入到RF里进行训练和测试,计算出3个恒星大气参数的预测值。

图1 卷积神经网络结构图Fig.1 Convolutional neural network structure

CNN对预处理好的恒星生成的“伪二维光谱图”进行特征提取之后,通过模型训练得到恒星光谱数据参数的预测值与真实值作差,通过二者之间的差值计算损失函数,并反向传播以训练模型参数,训练完成后用测试数据进行模型测试,验证模型的精确度。若出现误差太大,及时停止并通过网格搜索对网络的超参数(卷积核的大小、网络深度、神经元的个数、学习率等)进行优化。最终设置3组卷积层和池化层,其中卷积核个数分别为64 128和256,大小为9×9,卷积步长为1×1,模型的详细参数如表1所示。同时与典型回归算法中决策树(classification and regression tree, CART)、支持向量回归(support vector regression, SVR)、RF的预测结果进行对比。

RF回归层使用网格搜索优化参数进行优化,通过调整决策树的数量以及单棵决策树的特征数量来提高随机森林模型的性能,通过网格搜索并结合k折交叉验证(k=5)得到最终参数。根据实验结果比较,确定了形成随机森林树的数量(n_estimators=200)、形成叶节点(n_tree=10)所需的最小数据量以及损失函数(criterion=mse)。

RF的特征筛选层是基于后向(或前向)选择的贪婪算法,通过反复构建基层模型,选择一定比例重要性评分,排序靠后的变量进行剔除,直至达到某一标准或获得指定数量的变量个数。利用R2评分进行特征重要性的选择,它可以描述回归模型对因变量随输入变量变化的解释程度,其计算公式为

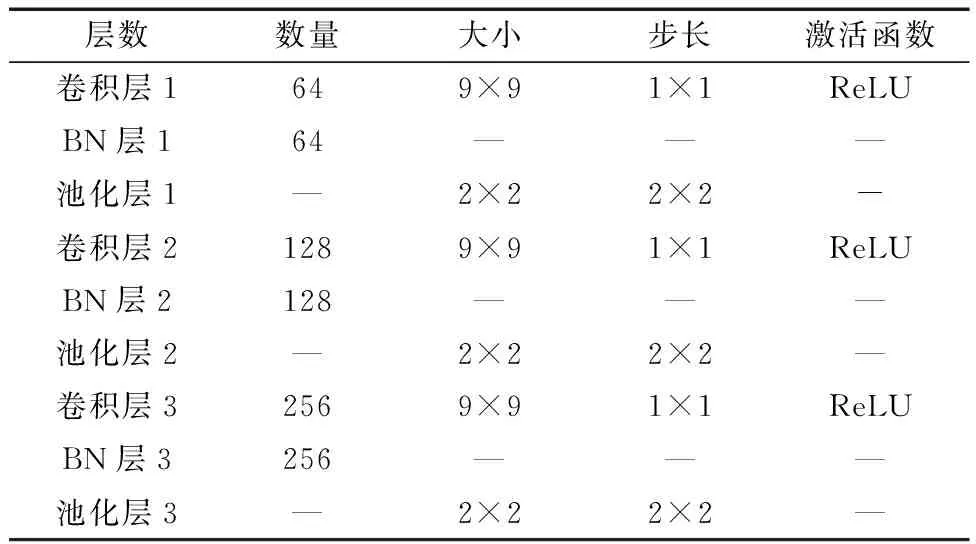
表1 模型结构参数Table 1 Model structural parameters

图3 CNN-RF网络结构图Fig.3 CNN-RF network structure diagram

(2)

SVR模型的参数是利用网格搜索进行优化进而选择了径向基函数(radial basis function),惩罚函数C和核函数参数Gamma。CART算法中的参数设置由学习曲线和网格参数进行调节。各预测模型的参数设置情况如表2所示。

表2 其他参数模型Table 2 Other prediction model parameters

CNN-RF算法的具体步骤如下。

(1)批量读取预处理之后的光谱数据,输入到CNN特征提取网络中。

(2)用一定大小的卷积核以固定步长读取整个“伪二维光谱图像”,将第一次卷积层得到的“伪二维光谱图像”下采样生成池化层;重复此步骤;再用池化后的二维光谱数据变为一维,从而获得训练样本和测试样本的特征向量。

(3)将CNN特征提取网络生成的特征向量作为RF回归器的输入特征,并划分为测试集与训练集;利用RF中的自助采样法在训练集上采样,对每个决策树生成其对应的训练子集,并对决策树进行训练,在每个内部节点上选择最优属性进行分裂。

(4)对于测试集,用RF回归器进行测试,得到其中一个恒星大气参数的预测结果。另外两个恒星大气参数的结果预测进行相同操作。

3 实验

3.1 数据集以及预处理

本文要处理的光谱属于一维形式(如图4所示),其形式可以看作是一个由高达数千个属性构成的向量。所用的数据来自于中国科学院国家天文台运营的郭守敬望远镜(LAMOST)项目。从LAMOST官网中下载所需的一维光谱文件,该文件存储方式为fits格式,同时下载对应的星表文件。从中筛选出信噪比r波段大于等于20的数据共56 683条,随机选择两万条作为本文实验数据。

图4 一维光谱图Fig.4 One-dimensional spectrogram

光谱数据处理过程如下。

(1)首先利用MATLAB将fits文件和星表文件进行匹配,读取fits文件的流量和波长以及所对应的3个恒星大气参数。

(2)对一维光谱进行数据预处理,包括初步筛选、插值和归一化,将数据变成4 096个分量。归一化处理的目的是将数据特征映射到同一尺度中,有利于网络的训练,从而提升精度。本文选择min-max归一化法,也叫离差标准化,是对原始数据的线性变换,即

(3)

式(3)中:F′为标准化之后的恒星光谱流量;F为原始恒星光谱流量;Fmax和Fmin为原始恒星光谱流量的最大值和最小值,将恒星光谱流量转化为0～1的区间,测试数据也做类似的处理。

(3)为了能够利用CNN来处理该一维光谱,使用文献[14]所提出的S型折叠方法将一维光谱转换成“伪二维光谱”,可以看作是一种保留一维光谱所有信息的伪图像。将归一化后的光谱通过“S”型折叠转换为64×64的二维矩阵,形成“伪二维光谱图”,如图5所示。

(4)最后随机选择20 000条数据进行训练和测试,每次实验时都是随机选择总光谱的70%作为训练数据,其余的30%作为测试数据。本文所选实验数据中三大参数本身的覆盖区间范围为:Teff:3822.52-8471.59 K、Logg:-0.054～4.9 dex、Fe/H:-2.473-0.757 dex。

3.2 实验环境

本文使用的预测模型均基于python语言实现:使用pytorch深度学习框架搭建CNN-RF和CNN模型,其他对比模型是用scikit-learn库搭建。处理器为Intel(R)Core(TM)i5-7500 CPU @2.90 GHz。系统类型:Windows 10旗舰版64位。

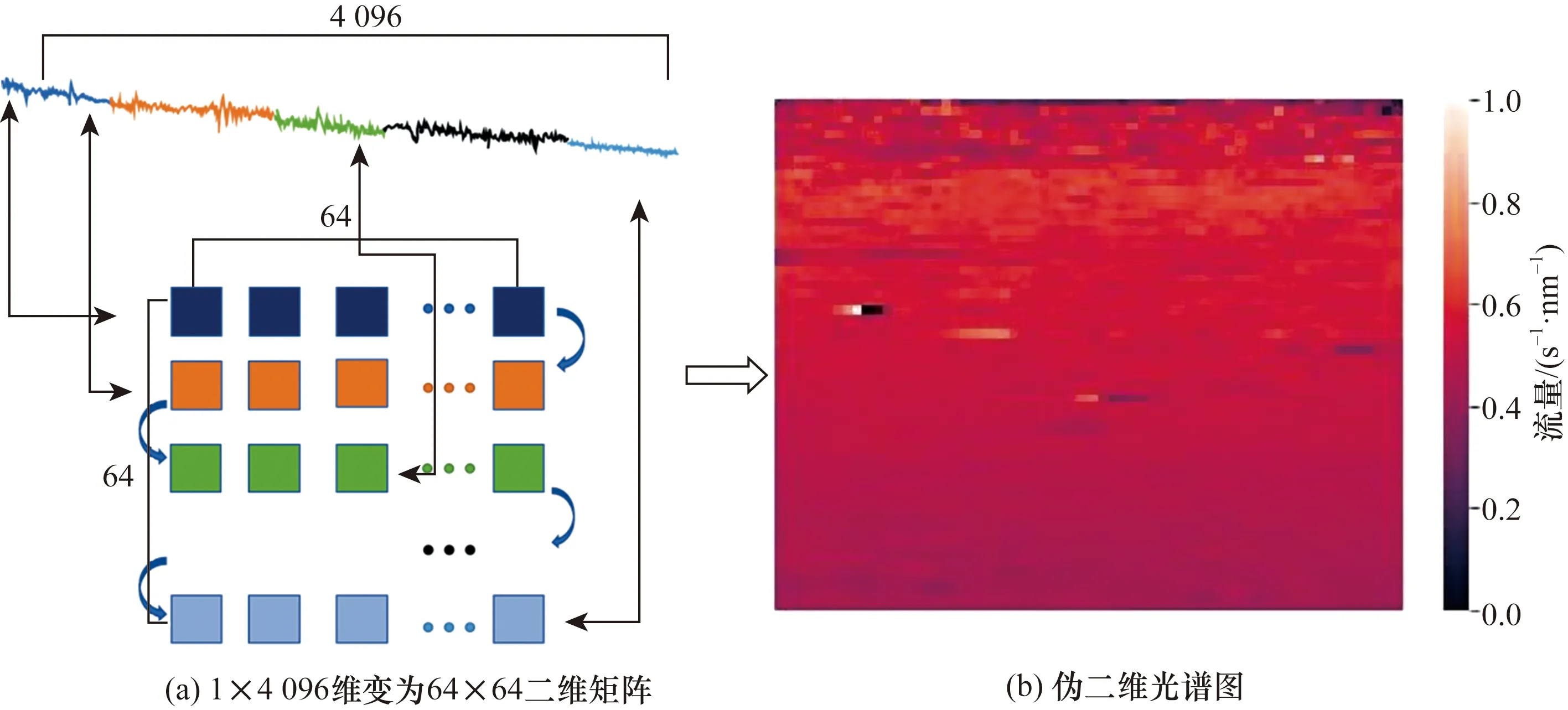
图5 一维光谱数据变成“伪二维光谱图”Fig.5 One-dimensional spectral data becomes “pseudo-two-dimensional spectral map”

3.3 评价指标

为了准确评价上述模型的预测性能,引入平均绝对误差(mean absolute error, MAE),标准差(standard deviation, SD)作为预测性能的评价指标,MAE直观反映了预测值与实际值的偏差,其数值越小,模型的预测性能越好;SD反映回归预测的离散程度,表达式为

(4)

(5)

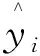
3.4 实验结果分析

图6～图8所示为CNN-RF、RF、SVR、CART的回归模型预测的有效温度(Teff)、表面重力(Log g)、金属丰度(Fe/H)估计值和真实值对比图以及每个参数测量误差的分布直方图。4种模型的Teff、Logg、Fe/H的平均绝对误差、标准差和R2的实验结果如表3所示。

(1)有效温度(Teff)的预测结果对比图和残差分布直方图:从表3可以看到CNN-RF、RF、SVR、CART的有效温度的平均绝对误差分别为123.65、131.95、130.49、151.04 K,CNN-RF最小。从图6所示测量结果对比图和误差直方图中,可以看到CNN-RF的预测值和真实值均匀地分布在y=x上,并且在残差图中可以看到CNN-RF基本上都接近零点中心。与对比实验的图相比,有明显的聚合性且离散程度较小,但因4种算法之间的平均绝对误差相对较小,因此在图中的直观中反应并没有很大的差别。

表3 4种算法的MAE和SD以及R2统计表Table 3 MAE, SD and R2 statistics of the four algorithms

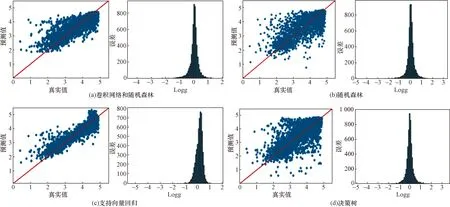
图7 4种算法下Logg的预测值和真实值对比图和误差统计直方图Fig.7 Comparison of predicted and true Logg values and histogram of error statistics under the four algorithms

图8 4种算法下Fe/H的预测值和真实值对比图和误差统计直方图Fig.8 Comparison of predicted and true Fe/H values and histogram of error statistics under the four algorithms

(2)表面重力(Logg)预测结果对比图和残差分布直方图:由表3中可以看到CNN-RF、RF、SVR、CART的表面重力(Logg)的平均绝对误差分别为0.205 5、0.244 2、0.243 2、0.269 1 dex,CNN-RF的精度最高。因为Log g数据本身的分布范围相对较小,所以整体的差别并不是很大。从图7所示预测值和真实值对比图和残差分布图的结果中可以看出,数据基本上分布在y=x附近,残差图分布比较紧凑,离散程度较低。

(3)金属丰度(Fe/H)预测结果对比图和误差直方图:由表3中可以看到CNN-RF、RF、SVR、CART的金属丰度(Fe/H)的平均绝对误差分别为0.148 6、0.175 9、0.204 4、0.202 4 dex,从图8中可以看出,CNN-RF的结果与经典回归拟合算法相比,精度较高。从图8所示预测值和真实值对比图和残差分布图的结果中可以看出,RF、SVR、CART预测的表面重力均带有不同程度的离散,并没有均匀的分布在y=x这条直线上,效果相对较差。

由表4可以看出CNN-RF相比于RF、SVR、CART在3个参数上均有提升,从而验证了本文算法的有效性。另外从表3中可以看出RF在测量3个参数时的MAE相较于SVR、CART相对来说精度较高,从侧面验证了RF算法的优越性,进而表明了CNN和RF的结合在一定程度上是可行的。

最后,实验结果表明本文提出的CNN-RF算法在三大物理参数Teff、Logg、Fe/H的测量结果评价指标中相对于其他3种传统算法都有较大的提升,一定程度上说明了CNN-RF算法能够较好地应用于恒星大气参数的自动测量。在模型泛化性能方面,CNN-RF的R2在Teff和Fe/H结果中最优,Logg次之,说明本文提出的CNN-RF模型回归预测综合性能最优,模型的有效性及拟合能力得到验证。从预测值和真实值的对比图和误差直方图来看, CNN-RF算法大部分数据对比结果都均匀的分布在基准线y=x上,说明模型的拟合能力相对较好,而误差直方图显示出CNN-RF的系统误差相对更接近于零,从而说明本文方法预测结果分布更为合理。

表4 精度提升百分比统计表Table 4 Accuracy improvement percentage statistical table

4 结论

针对恒星大气参数自动测量问题的现实需求,利用CNN对二维图像的优秀特征提取能力和经典回归网络的回归拟合能力,提出了一种卷积神经网络和随机森林相结合的恒星大气参数测量算法CNN-RF。该方法得到的预测结果拟合程度更好并且具备更小的误差,能够利用光谱数据准确有效的对恒星大气参数进行测量。为了验证构建CNN-RF回归预测模型的有效性以及泛化性能,与3种经典的机器学习算法SVR、RF、CART模型进行了性能对比,实验结果验证了本文方法具有更高的精度,证明了本文方法能够有效用于恒星大气科学参数的自动测量。