自适应多目标遗传算法的集成剪枝用于人脸表情识别

陈 星,李丹杨,何 庆

(贵州大学 大数据与信息工程学院,贵州 贵阳 550025)

人脸表情识别主要通过眼睛、嘴巴、眉毛和其它人脸特征识别人类个体的内在情感[1]。人脸表情识别在心理学、人机交互以及自动驾驶等领域[2-4]具有重要作用。当使用表情图片进行情感分析时,其结果受图片亮度、图片完整程度、拍摄者的种族以及拍照角度等因素影响,从而增加了表情识别难度,因此需要继续进行人脸表情识别研究并提高识别效果。

研究表明,使用多分类器的集成学习比使用单一分类器在人脸表情识别领域具有更高的准确率和鲁棒性[5-6]。然而,集成学习也带来了一些问题。基分类器池包含一些低识别率和冗余的分类器,它们会降低识别效果并增加存储空间和运行时间的负担。因此,解决此问题的集成剪枝研究逐渐兴起。集成剪枝从基分类器池中剔除弱分类器和冗余分类器,将最优能力的分类器保留下来进行集成,相比于集成学习,该方法在降低算法时空复杂度的同时提高了最终的识别效果。然而,从全局搜索空间找到最优的分类器子集仍是一个需要不断研究的问题。

进化计算技术因其在整个搜索空间强大而高效的搜索能力受到了广泛关注[7]。进化计算技术采用基于种群的随机搜索方法将分类器选择视为一个寻求最优解的过程,进一步提高了选择最优分类器子集的能力。遗传算法[8]是一种经典且高效的进化计算方法,二进制编码方案的遗传算法可以较容易地找到合适的分类器子集,且搜索空间远小于其他进化计算方法。因此,本文使用遗传算法进行分类器的选择。

集成剪枝选择的分类器应是“好而不同”,需同时考虑两个评价指标,即最低错误率和最少的分类器数量,因此使用集成算法进行分类器剪枝变成了一个多目标优化问题。多目标优化问题的解通常来源于帕累托前沿(Pareto Front,PF)。图1给出了集成剪枝的双目标问题的PF,每一个点代表遗传算法的一个染色体,由二进制0-1编码构成,1代表选择对应分类器,0代表不选择相应分类器。在PF上的解都是集成剪枝问题的最优解。文献[9]证明了使用多目标遗传算法进行分类器剪枝可以有效提高人脸表情识别的准确率。NSGA-Ⅱ[10]是一种经典的多目标优化遗传算法,但在此算法的交叉策略中仍没有一种合适的策略既可以适合前期探索,又可以适合后期开发。

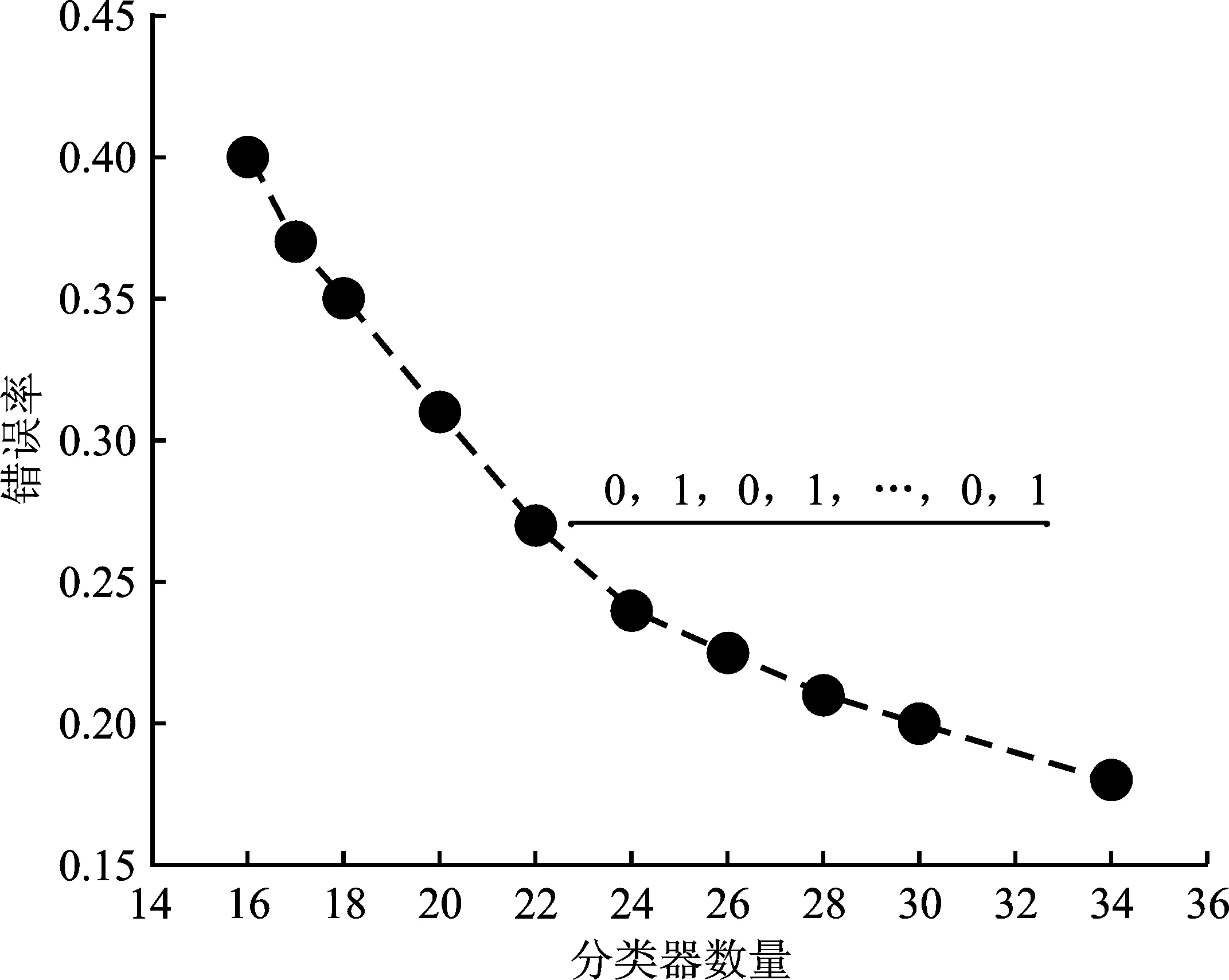
图1 集成剪枝的帕累托前沿分布Figure 1. Pareto front distribution with ensemble pruning

本文提出了一种自适应多目标遗传算法的集成剪枝(Adaptive Multi-objective Genetic Algorithm with Ensemble Pruning,AMGAEP),并将其用于人脸表情识别领域。AMGAEP是对NSGA-Ⅱ的改进,其改进主要有以下几个方面:1)AMGAEP从4种交叉算子中自适应地选择一种合适的交叉算子进行染色体的交叉操作,而不是始终使用一种固定交叉算子。该方法通过轮盘赌和贪婪优化的方法自适应地确定各个交叉算法的优先级,从而在算法的不同阶段选择不同的交叉算子,其目标是充分利用不同交叉算法的搜索能力,选择一组数量少、分类精度高的最优分类器子集。2)AMGAEP考虑了交叉概率和变异概率随着算法更新过程也应该进行动态变化的情况,并设计了一种新的变异概率计算机制。3)AMGAEP使用一种最新的拥塞距离计算方法,促进了PF上解均衡分布。

1 AMGAEP算法

为提升人脸表情识别的性能,本文提出了AMGAEP,其框架如图2中所示。首先,采用训练集和验证集构建基分类器池;然后,使用多目标遗传算法在验证集的预测标签中生成PF;最后,利用测试集在PF中测试各个解的效果并找到最优解从而获得最终的决策结果。

图2 AMGAEP的流程Figure 2. Flow of AMGAEP

1.1 生成基分类器

集成剪枝的有效性在较大程度上依赖基分类器的多样性和错误率,多样性越高且错误率越低,集成剪枝的效果就越好。卷积神经网络(Convolutional Neural Network,CNN)在人脸表情识别领域已经取得了不错的识别效果[11-12]。为了保证最终集成剪枝的误差较少,本文采用CNN作为基分类器,同时通过改变CNN的参数和网络结构来满足基分类器多样性的要求,CNN结构如图3所示。

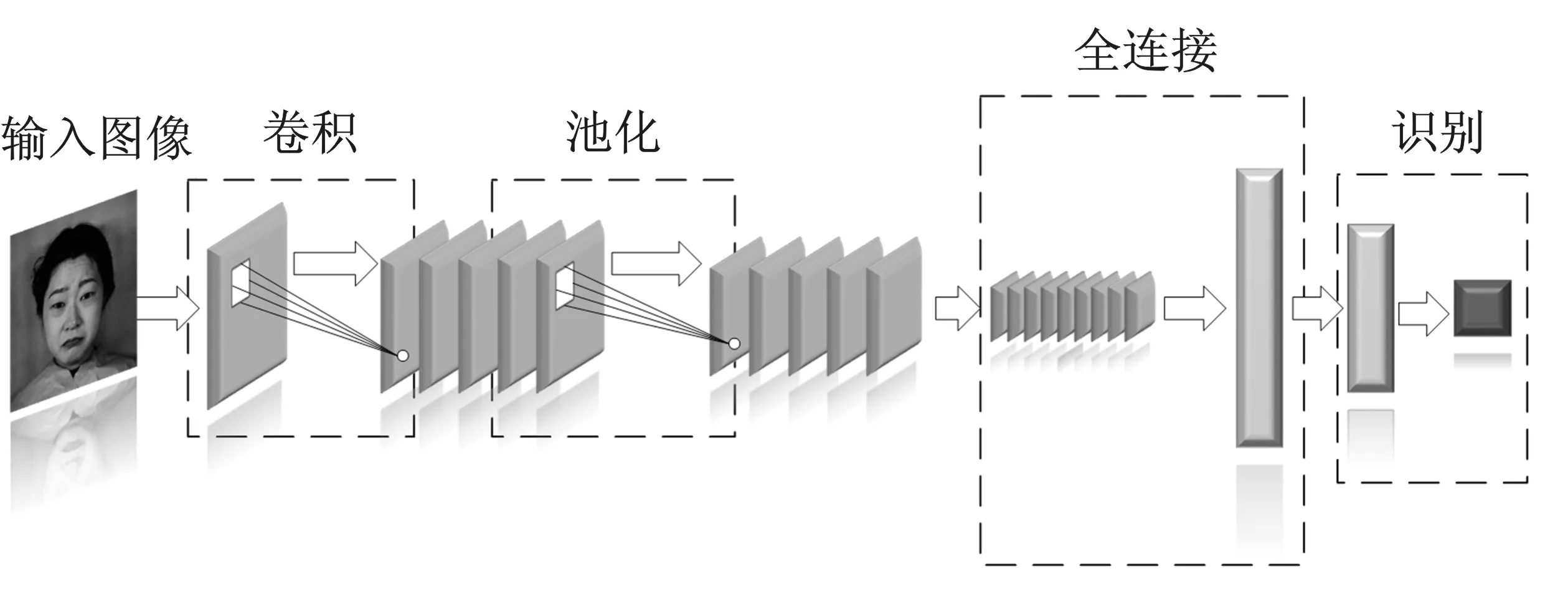
图3 CNN结构Figure 3. Structure of CNN

本文使用TensorFlow深度学习框架构造了231个不同的CNN模型,每个CNN模型包含k层。其中,前两层被固定为卷积层和池化层,最后一层被固定为Softmax层。CNN模型的每一层包含较多参数,例如卷积核的大小、池化核的大小和随机失活等,参数的取值范围如表1所示。

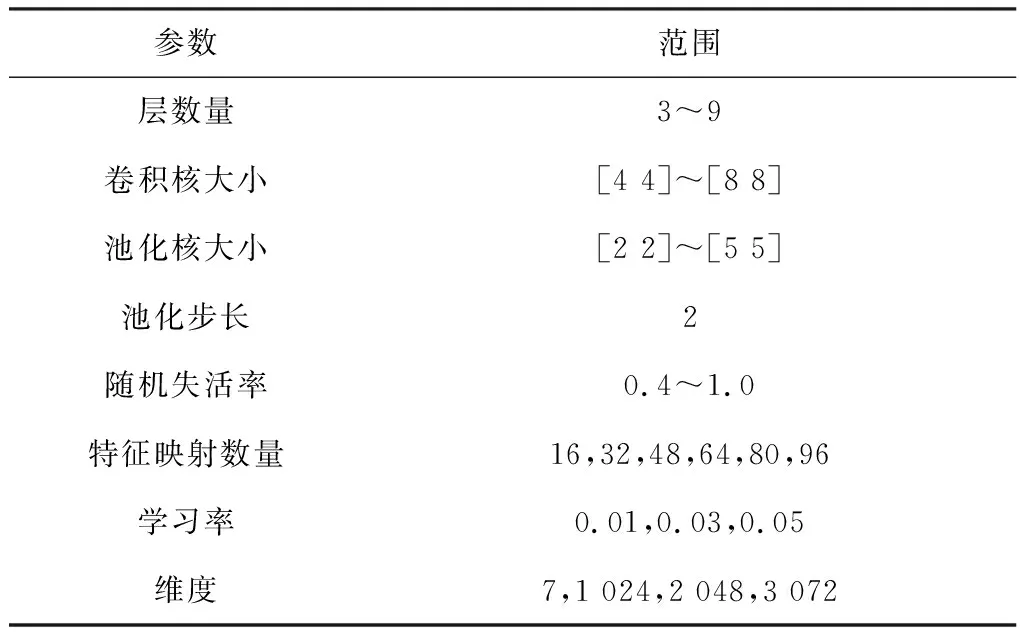
表1 生成的CNN模型参数范围

1.2 生成分类器对样本的预测值

本文使用cj(xj)表示j个分类器对i个样本实例的一个预测值,则预测矩阵P∈Rm×n如式(1)所示。

(1)

1.3 多目标二进制遗传算法

AMGAEP使用多目标遗传算法对基分类器池进行分类器的剪枝,将选择分类器过程视为最优分类器子集过程。

1.3.1 种群初始化

本文直接使用二进制编码,即0-1编码来进行分类器选择问题。如果一个染色体的编码为100001,则表示选择第一个和最后一个分类器进行集成。

1.3.2 目标函数

AMGAEP从分类器池中选择出来的分类器要满足“好而不同”的特点,即选出来的分类器不仅错误率低,而且满足数量少的特点,因此本文使用分类器的错误率和选择分类器的数量作为目标函数。错误率err的目标函数为

(2)

其中,X是一个解;NError和NAll分别为样本中错误预测实例和所有实例的数量。

选择分类器数量的目标函数为

(3)

其中,xi是一个染色体第i个值;D是分类器的数量。

1.3.3 新颖的动态突变率更新策略

本文目标为算法在探索前期进行更多地突变以便进行更全面地全局搜索,而在探索后期尽量减小突变的发生,避免跳出最优值,因此AMGAEP设计了一种自适应步长的方法,使得突变概率能够随迭代次数自动变化。突变概率pu的计算式为

(4)

其中,δ一个可变参数,本文设为0.1;t是当前迭代次数;maxIter是最大迭代次数。突变概率的动态变化如图4所示。

图4 突变率动态更新曲线Figure 4. Dynamic update chart of mutation rate

1.3.4 新颖的自适应交叉策略

染色体交叉就是交换父代染色体并重新组合从而生成新的子代染色体的过程,常见的二进制交叉有单点交叉[7]、双点交叉[7]、均匀交叉[7]和卡牌交叉[7]等。本文使用上述4种交叉操作作为基本的交叉策略,并引用轮盘赌和贪婪的方式进行染色体自适应交叉操作。

首先,该方法将4种策略的优先级设为1,每个策略的优先级随着搜索阶段的变化而变化。其次,根据每个策略的优先级大小,该方法通过轮盘堵的方式选择合适的交叉策略。优先级越大代表被选择的概率越高。同时,本文使用贪婪的策略进行优先级的更新,当一种交叉策略生成的子代染色体支配父代染色体时,该优先级会加1。策略被选择的概率描述为

(5)

其中,PAi是第i个交叉策略被选择的概率;si是该策略的优先级。如果一个策略生成的子代支配其父代,表明该策略适合当前搜索阶段,可增加该策略的优先级。

如图5所示,圆中的每个扇形区域代表一个交叉策略(S1、S2、S3、S4)的优先级,策略优先级越高,所占的比例越大,表示该策略被选择的概率越大。初始时,每种策略的优先级相同,随着探索深度的增加,每个策略的优先级会发生变化,优先级的值会变得不同。根据式(5)可得到相应策略被选择的概率,因此每个策略被选中的概率也会不同。在算法每一代结束时,重新初始化每个策略的优先级,以防止当前一代的策略选择影响到下一代。交叉策略自适应选择与更新的详细描述如算法1所示。

算法1 自适应交叉策略选择与更新输入:策略优先级Sm,m∈{1,2,3,4},父代总群。输出:策略优先级Sm,m∈{1,2,3,4},两个子代。1.用式(5)计算每个策略被选择的策略SPm2.轮盘赌选择一个策略SPm3.ifSPm==14. 使用单点交叉策略生成两个子代5. if有一个子代支配一个父代6. s1=s1+17.else if SPm==28. 使用双点交叉策略生成两个子代

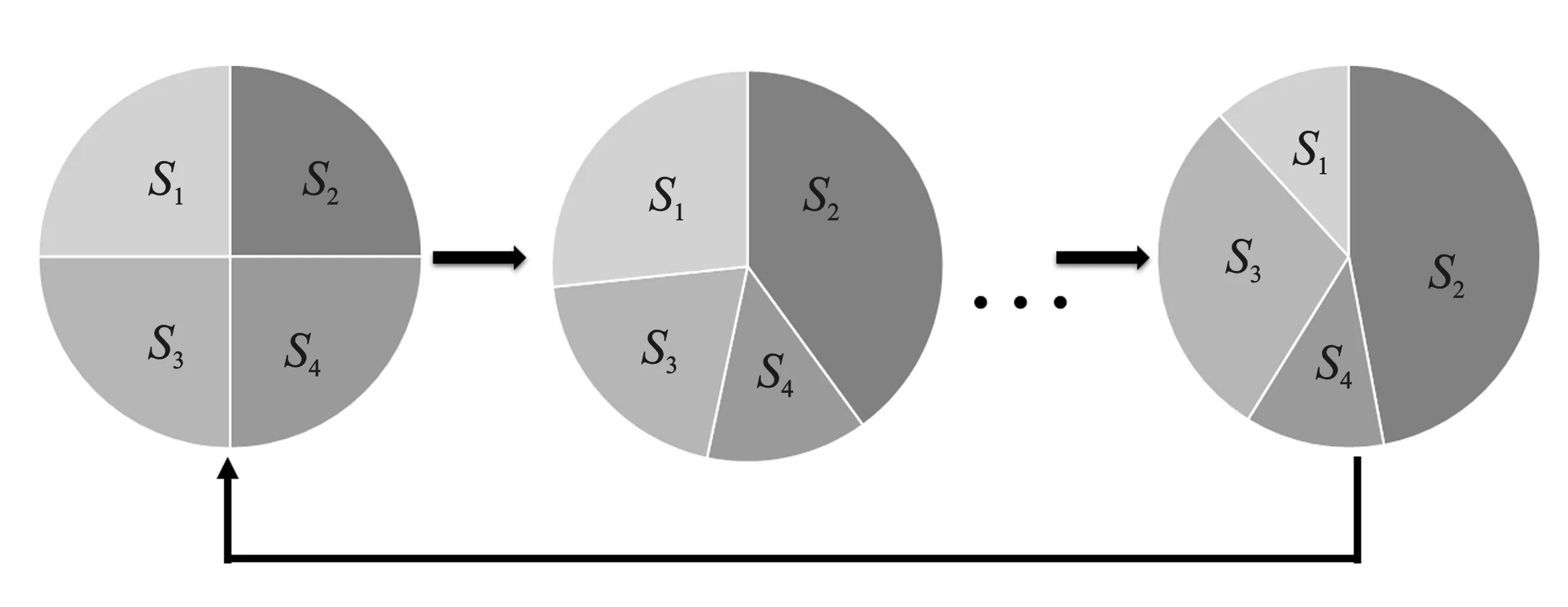
图5 轮盘赌优先级Figure 5. Roulette plugging priority

1.3.5 AMGAEP的其他部分

在算法的染色体选择阶段,AMGAEP使用锦标赛选择方法选择两个子代种群,每个子代种群的数量是父代种群的一半,将两个子代种群合并得到一个大小和原始父代种群一样的子代种群。

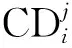
(6)

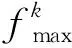
本文使用文献[14]所提方法计算染色体在探索过程中的交叉概率,实现交叉概率的动态更新,交叉概率pc的计算式为

(7)

其中,pc0是一个控制因子,控制交叉概率的变化程度,本文设为0.8;c是一个可调参数,本文设为0.5;t是当前迭代次数;maxIter是最大迭代次数。

在算法的其他部分,AMGAEP与原始NSGA-Ⅱ保持一致。AMGAEP算法的标准处理过程如算法2所示。

算法2 AMGAEP输入:训练集T={(xi,xj)}ni=1,验证集V={(xi,xj)}ni=1,测试集T={(xi,xj)}ni=1。输出:集成剪枝错误率err,最优的分类器子集cls={ci(x)}ki=1。1.使用训练集训练一组基分类器C={ci(x)}mi=1

1.4 大多数投票

本文主要研究分类器的选择,因此分类器的集成使用一种简单策略,即大多数投票法,其计算式为

(8)

其中,e=1,2,…,7;k是分类器的数量。如果分类器j对样本i的预测值等于e,则φ(·)=1,否则φ(·)=0。

2 实验

本文实验电脑配置如下:Windows系统及主频为2.3 GHz Intel i7-11800H 的CPU和NVIDIA RTX3060显卡。

2.1 数据集

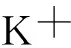
表2 5个数据集中每种表情的详细信息

2.2 数据集在集成剪枝中的使用

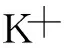
AMGAEP在每个数据集上各自进行10次实验,将10次实验得到的帕累托前沿进行组合,再将组合的结果进行非支配排序,从而得到新的帕累托前沿并将此作为10次实验的结果。将最大迭代次数maxIter设为500,种群大popsize设为300。

2.3 AMGAEP在集成剪枝中的效果

在得到的PF中,将两端的两个解剔除,用测试集测试其余解的性能,挑选错误率最低的解作为本文方法获得的最优解,从而得到集成剪枝的错误率和分类器子集数量。

本文算法对分类器进行剪枝,剪枝前后分类器的分布情况如图6所示,图6(a)和图6(b)分别为集成剪枝前后基分类器的错误率分布情况。

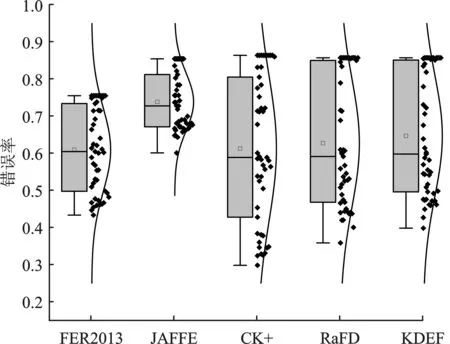
(a)

图6中的小黑点表示存在相应的分类器有对应的误差值。图6(b)是误差值分布的正态曲线。由图6可知,剪枝后的分类器数量明显减少且主要集中在错误率更低的区间。但剪枝后仍存在一部分弱分类器,由于本文使用大多数投票进行集成,因此较少部分分类器不会影响最终的集成效果。

如图7所示为5个数据集中7种表情的归一化混淆矩阵,图中行代表真实标签,列代表预测标签。元素越大,主对角线上的颜色越深,表示预测标签和真实标签之间的一致性越高,某个表情的识别率越高。

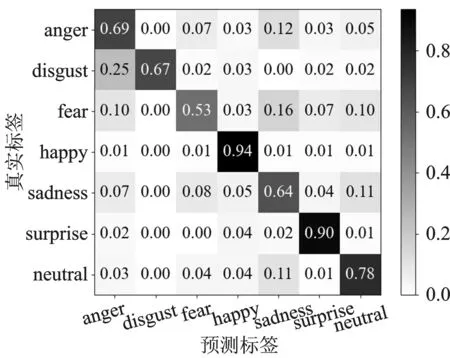
(a)

2.4 AMGAEP与其他集成剪枝方法的对比

将AMGAEP在5个数据集上与一些集成剪枝方法进行了比较,结果如表3所示。

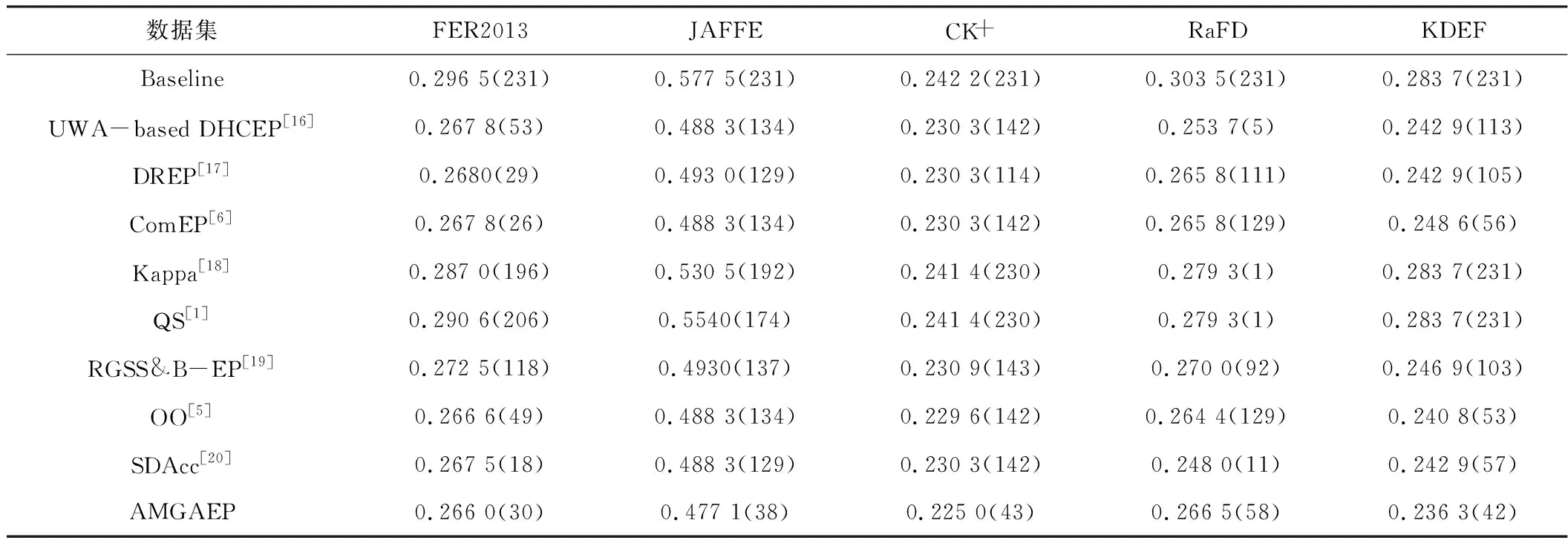
表3 AMGAEP与8种集成剪枝方法的错误率比较

2.5 基分类器性能对集成剪枝的影响

为验证基分类器性能的好坏影响集成剪枝的最终结果,本文使用EfficientNet[21]和ConvNeXt[22]作为基分类器,通过更改其参数获得了30个不同的基分类器模型,包含10个EfficientNet模型和20个convNeXt模型。增加优质分类器数量会增加集成剪枝的性能且在任何一个数据集上均具有相同效果。本文仅在KDEF数据集上进行实验,这30个模型在KDEF数据集上的错误率为0.23～0.28。将这30个基分类器与之前的231个基分类器组合,从而构成了一组新的基分类器池,共计261个基分类器。

在新的基分类器池中,AMGAEP在KDEF数据集上的结果如表4所示。与表3相比,在新基分类器池中具有更低的错误率,说明基分类器模型性能的好坏影响集成剪枝的最终识别结果。

表4 AMGAEP在新基分类器池中的效果

在新的基分类器池中,AMGAEP在KDEF数据集上的归一化混淆矩阵如图8所示。与图7(e)相比,在新的基分类器池中,本文方法对disgust 和 fear具有更高的识别率,进一步说明了基分类器性能越好,集成剪枝的效果越好。然而,AMGAEP并未在新基分类器池中取得显著性提升,这是因为基分类器池中的弱分类器会影响集成剪枝的识别结果。提升集成剪枝的整体效果需要向基分类器池中添加更多具有多样性的优质分类器,提高集成剪枝的基线,从而取得更好的识别效果。

图8 AMGAEP在KDEF数据集中的归一化混淆矩阵Figure 8. Normalized confusion matrix of AMGAEP in the KDEF data set

3 结束语

本文提出了一种新的自适应多目标遗传算法用于分类器的剪枝,提出了新的自适应突变概率计算式,以获得一组分类器数量更少、学习能力误差更低的分类器子集。在交叉策略自适应阶段,使用轮盘赌和贪婪策略动态更新每个交叉策略的优先级,根据优先级计算每个策略被选中的概率,从而在算法探索开发过程中自适应地选择合适的交叉算子生成子代,增强算法在搜索空间的探索能力。突变概率的动态更新使得所提算法在探索阶段更注重全局搜索,而在后期阶段则侧重于局部开发。在5个真实人脸表情数据集上将本文提出的AMGAEP与一些集成剪枝方法进行对比。实验结果表明,AMGAEP可以选出误差更低、冗余度更小的分类器子集,提升集成剪枝的效果。

在未来的工作中,本文将考虑使用更多的表情图片去训练基分类器以降低分类器模型过拟合的影响。同时,在基分类器池中添加最新的神经网络模型以提高识别效果。最后,本文考虑将方法应用于公共安全和健康领域去增加该方法的泛化能力。