一种用于变压器故障诊断的卷积神经网络优化方法

汪徐阳,易映萍,李田丰

(上海理工大学 机械工程学院,上海 200093)

油浸式电力变压器是电力传输和能量转换的枢纽设备,电力变压器的运行故障是导致系统大面积停电的关键之处,及时、准确发现变压器的早期潜伏故障对确保电网安全、稳定运行具有重要作用[1]。油中溶解气体分析(Dissolved Gas Analysis,DGA)是检测油浸式变压器内部绝缘潜伏性故障诊断的关键技术,通过对油中溶解气体浓度及比例进行在线监测可及时发现内部隐患。基于DGA的分析方法有传统三比值法、IEC三比值法、大卫三角形法以及Rogers比值法[2]等,这些方法均先按特征气体的比例编码,然后进行相应的故障诊断。故障诊断方法大致分为基于模型、信号处理[3]以及数据驱动3种,而数据驱动方法可以用于难以建立精确模型或提取信号特征的复杂系统。为了充分挖掘海量数据价值,基于数据驱动的机器学习方法已广泛应用于变压器故障诊断领域,包括BP神经网络(Back Propagation Neural Network,BPNN)[4]、支持向量机(Support Vector Machine,SVM)[5]、模糊逻辑(Fuzzy Logic,FL)[6]等。上述浅层机器学习模型克服了传统三比值法的不足,但都存在算法原理简单以及对于数据量的要求较小等问题,容易造成特征不足,陷入局部最优的后果。

深度学习作为机器学习的一大分支,具有自主学习能力,能够实现基于高维数据的抽象表达与分类。与浅层的机器学习模型相比,深度学习能够有效提取样本特征,泛化能力更强。深度置信网络(Deep Belief Networks,DBN)、波尔兹曼机(Restricted Boltzmann Machine,RBM)和卷积神经网络(Convolutional Neural Network,CNN)是常用的深度学习模型。文献[7]利用DBN分类器对变压器的故障类型进行分类,该方法具有良好的特征提取能力和自适应性。文献[8]提出了一种基于分类受限玻尔兹曼机(Classification Restricted Boltzmann Machines,CRBM) 的故障诊断方法,在保留原始特征的基础上将诊断准确率以概率形式输出。随着更加深层次的探究深度学习,研究者发现使用卷积神经网络可以减少网络深度,提高泛化能力,使准确率大幅度提高。CNN是一种经典的深度学习模型,可以自动学习样本特征,将特征进行提取分类,在图像分类、语义分割等热点研究领域得到了广泛应用。文献[9]提出了代价敏感的一维CNN(CS-1DCNN)训练过程以便更多关注少数群体,准确率仅为88.41%。文献[10]提出了一种利用RGB原理构造二维动态图,将特征气体的百分比作为输入进行识别训练,具有较好的分类效果,准确率达到90%。

本文提出了一种数据增强方法,通过改变矩阵维度,将原始一维时间序列数据转换成二维图像,利用例如LeNet-5模型之类的二维卷积神经网络来进行图像识别。本文详细介绍了基于二维卷积神经网络的故障诊断优化策略,包括数据增强、卷积神经网络结构参数的选择与调整以及神经网络优化算法的选择,最后对模型进行训练以验证改进模型的诊断准确率。

1 基于二维卷积神经网络的故障诊断方法

一维卷积神经网络模型容易在特征提取时出现特征丢失和过拟合现象,因此需要加深神经网络深度来获取更大的感受野。本文采用LeNet-5网络结构,如图1所示的二维卷积神经网络结构在图像处理领域广泛使用,可较大程度地保留原始样本特征。

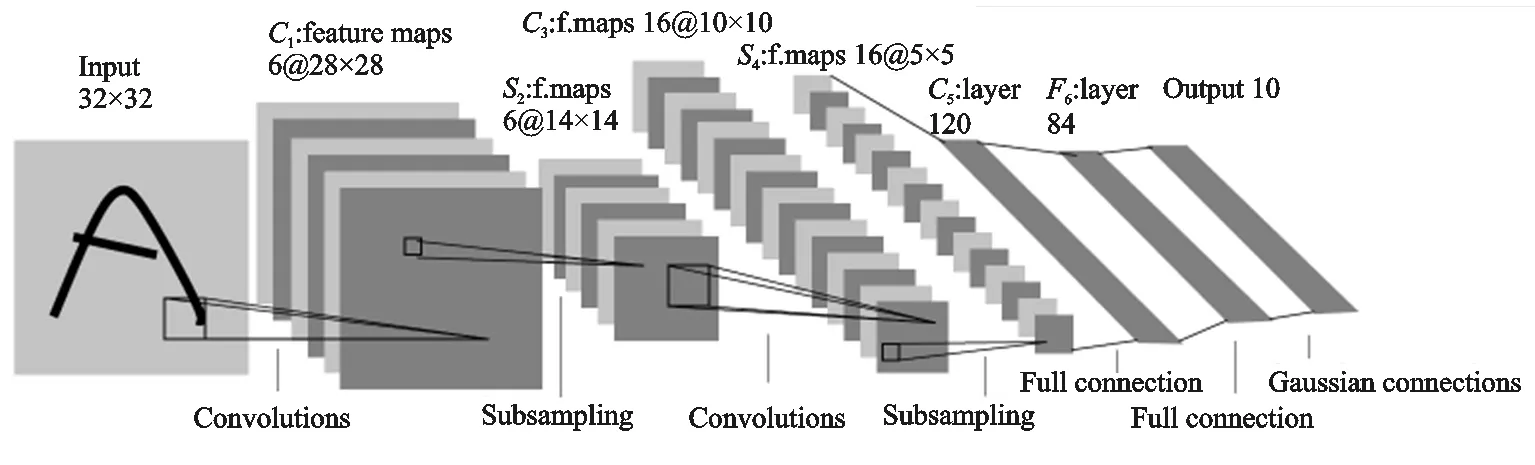
图1 二维卷积神经网络LeNet-5网络结构Figure 1. LeNet-5 network structure of two dimensional convolutional neural network

基于二维卷积神经网络的故障诊断流程如图2所示,对于原始训练样本进行扩充,转换为二维图片输入到卷积神经网络中,在训练完毕的网络中输入测试样本,进行训练优化以得到目标类别。

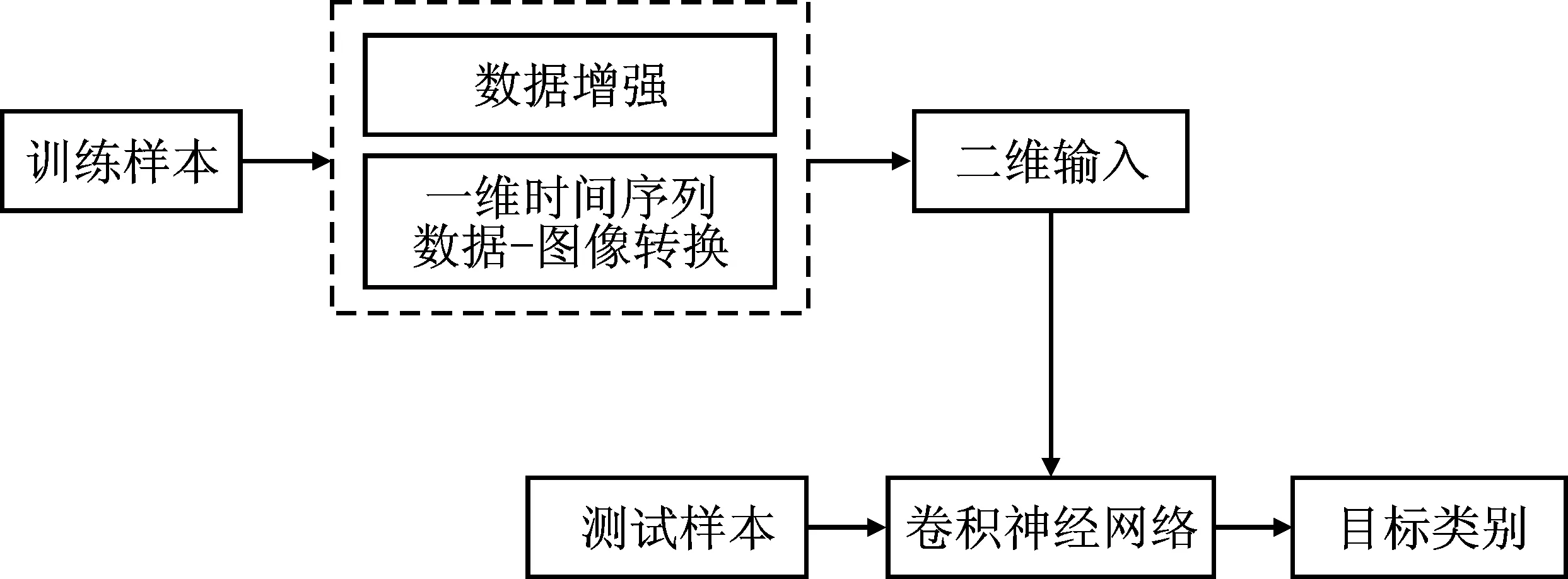
图2 变压器故障诊断流程Figure 2. Flow of transformer fault diagnosis

1.1 数据预处理

本文采用的变压器特征气体数据存在数据量少和样本不均衡等问题,而深度学习网络模型训练需要海量的数据支持,数据量直接影响网络模型测试精度。一维卷积神经网络只能对数据进行归一化处理,依然不能解决数据特征量少的问题。为了满足卷积神经网络模型的训练要求,使模型对具有同一规律的学习集以外的数据也能给出合适的输出,提高诊断精度,本文在现有数据的基础上对数据进行扩充。

先对样本数据进行筛选,删除一些无标签和特征数据丢失的无效数据,再进行数据增强。得到相对平衡的数据集后,根据卷积神经网络的输入要求将样本转化为二维的10×10矩阵,在输入二维信号的基础上可以使用在图像分类领域应用广泛的二维卷积神经网络。将一维数据集转化为二维图像的具体步骤如下:

设一组特征气体样本值xi为{x1,x2,x3,x4,x5},xi∈R1×5,每个xi分为整数和小数部分,各扩展为10位的二进制数。

整数部分按正序除2取余数,直至商为0,得到xii。小数部分按逆序乘2取整数,直至第10位,用到了mod函数,得到xij。最后将xii和xij合并为20位二进制数,xi即为100×1的一维数据。

数据集最后是以[None,100]的数据格式存放,针对卷积神经网络,需要保存图像的位置信息,因此在神经网络的输入端对数据样本进行重构,将其转化为[None,10,10,1]的二维图片格式输入到模型中进行训练。

1.2 构建二维卷积神经网络模型

在二维卷积神经网络结构中,有局部感知域、权值共享和池化3个基本工作机制。在网络结构中,输入层到隐藏层的映射为特征映射(Feature Map,FM),特征映射的权重为共享权值(Shared Weights,SW)。共享权值和偏置既可以保证在参数较少的情况下获取更大的感知野,又可以提升网络的深度,有效抑制过拟合。一般在卷积层后加入池化层,简化输出信息,与共享权值与偏置三者组成一个完整的卷积神经网络。最终使用如图3所示的二维神经网络结构来提取特征值。

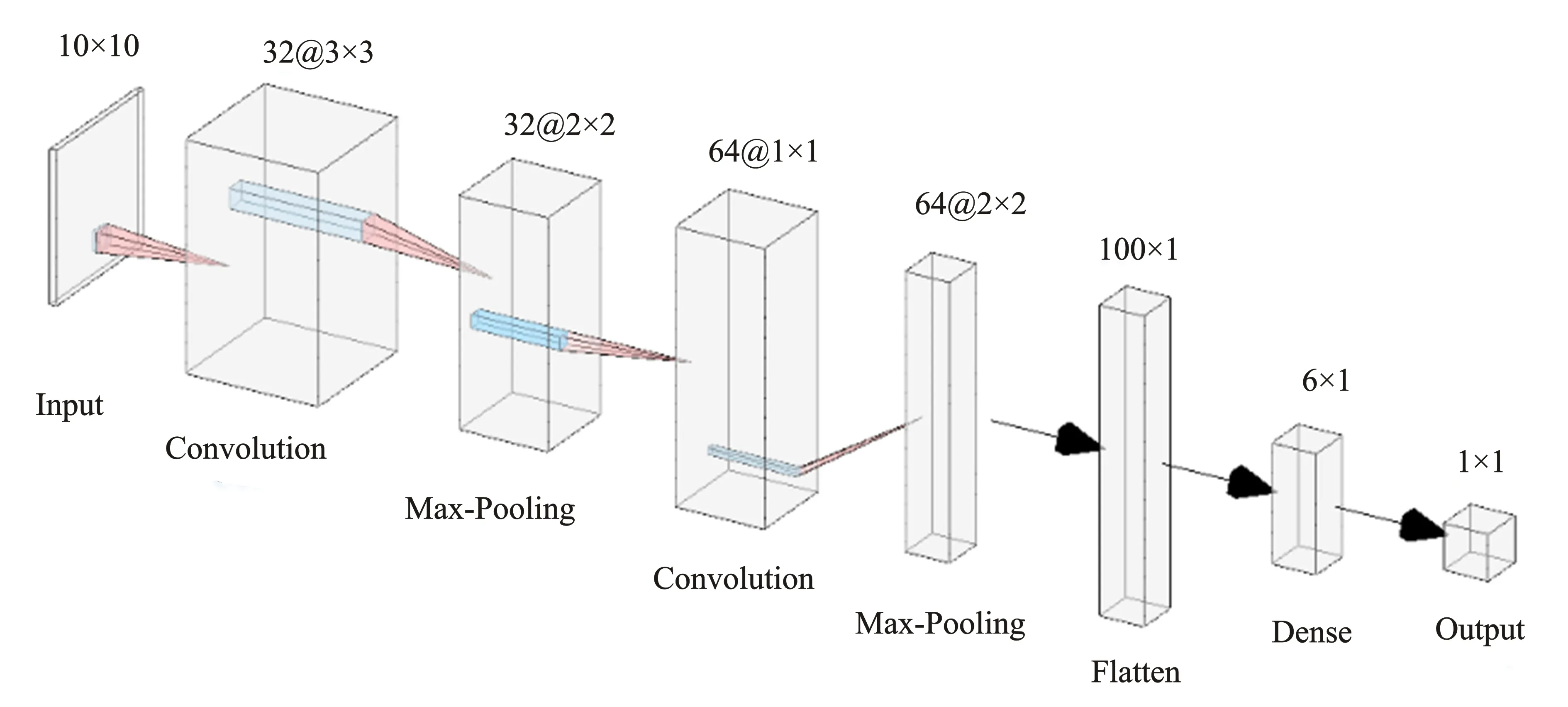
图3 二维卷积神经网络模型Figure 3. Two-dimensional convolutional neural network model

二维CNN故障诊断模型共有7层,每两层卷积层后添加一层采样层来保留主要特征,可减少计算量。考虑核个数、大小、步长与准确率的关系,设计二维卷积神经网络来实现端到端的训练和分类。二维卷积神经网络结构参数如表1所示。

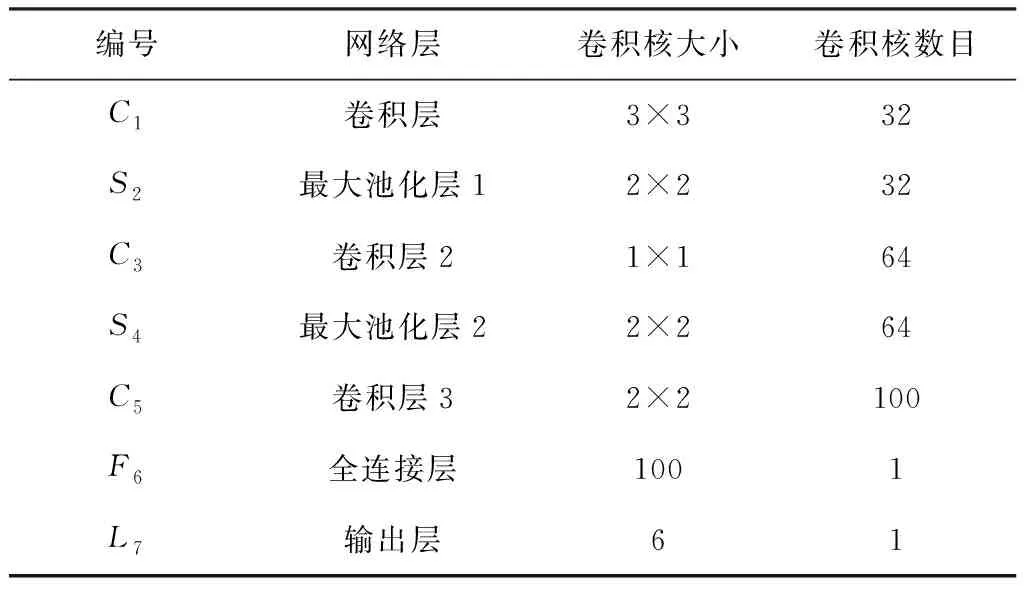
表1 二维卷积神经网络结构参数

第1层C1采用32个3×3的堆叠卷积层,卷积层特征的计算式如式(1)所示

(1)

其中,xi表示从第C1层到第S2层要产生的Feature数量,即3×3=9个;b代表Bias数量,本文设Bias为1;Padding设置为SAME边缘填0。

第1层池化层采用步长为2的最大池化(Max-pooling),用于缩小在卷积时获取的样本特征,从C1的深度可计算得出卷积层C1共有32×(3×3+1)个参数,再与前一个输入层的像素相连,共有8×8×320=20 480个连接。

对于S2的最大池化层,用2×2的最大池化可以减少特征的个数,对C1进行降维处理,将特征变为原来的1/4,此处共有32×2个参数,有16×14×4×4个连接(Connection),也减少了之后层的参数个数。

同样的提取方式,第2层卷积层为64个卷积核,可提取64个4×4的特征图,再经过S4得到64×2×2的特征图。

卷积层C5可将数据降维,得到100个1×1的特征图,加入Dropout层对模型进行正则化,全连接层有100个节点,采用传统Sigmoid激活函数。

最后在输出层中使用激活函数Softmax,将上一层的数据进行归一化,转化为(0,1)区间内的数值,作为多分类的目标预测值,将其转化为概率实现对变压器故障的分类。

1.3 基于改进Adam优化算法的CNN模型

在深度学习中,优化问题影响模型的泛化能力,两者紧密联系,因为模型收敛的最小值决定了模型泛化的程度,可以利用优化器对CNN模型参数进行管理并更新[11],使得模型输出与实际的诊断结果更加贴近。目前,在深度学习中较常用的梯度优化算法主要有SGD(Stochastic Gradient Descent)、RMSProp和Adam算法。

随机梯度下降SGD是较基础的神经网络优化方法[11],每次参数更新时仅选取单个样本计算其梯度,但由于样本的随机性,SGD会发生震荡使得训练不能收敛,在最小值附近波动。

设单个样本为(x(i);y(i)),其中x是输入数据,y是标签,计算式如式(2)所示。

θ=θ-lr×∇θJ(θ;x(i);y(i))

(2)

RMSprop是一种未发表的自适应学习率方法,对权重W和偏置b使用了微分平方加权平均数,并在更新W和b时使用除以根号求平均值的方法,使梯度大幅度减小,迭代过程如式(3)～式(6)所示

SdW=βSdW+(1-β)dW2

(3)

Sdb=βSdb+(1-β)db2

(4)

(5)

(6)

式中,SdW和Sdb分别是损失函数在前t-1轮迭代过程中累积的梯度动量;β是梯度累积的一个指数;RMSprop算法将学习速率除以平方梯度的指数衰减平均值,使网络函数收敛更快。

Adam是一种基于动量的算法和基于自适应学习率的优化算法[12],经过偏置修正,在每一次迭代过程中将学习率保持在一个固定区间内,能够保证参数的平稳性。从训练集中采包含m个样本{x(1),x(2),…,x(m)}的小批量,对应目标为y(i)。设完成一次学习之后的参数值为θ,衰减率为β1和β2,极小值为ε,初始学习率为lr。一般情况下取β1、β2的值分别为0.900和0.999,ε取值为10-8,而学习率需要在训练过程中结合实际情况及时进行调整,优化更新过程如式(7)和式(8)所示

mt=β1mt-1+(1-β1)gt

(7)

(8)

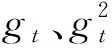
Adam梯度下降法更新梯度如式(9)所示。

(9)

由于在迭代初期误差较大,为了保证算法的收敛,通过修正梯度均值,减小误差对初始训练效果的影响。更新有偏一阶矩估计Mt和更新有偏一阶矩估计Vt如式(10)和式(11)所示。

(10)

(11)

参数更新计算式如式(12)、式(13)所示。

(12)

θt=θt-1+Δθt

(13)

测试误差θt+1为

θt+1=θt-vt-λlrθt

(14)

式中,λ为权重衰减系数;λlrθt为额外的权重衰减项。

Adam算法是目前神经网络架构中效果比较显著的自适应学习率优化方法[13],但该算法在保证准确率的同时也会产生测试误差,或者发生震荡错失全局最优解。本文通过添加到损失函数中的权重,更新卷积神经网络中的权值和阈值来提高衰减效果[14-15],改进后的参数值如式(15)所示。

(15)

改进后的Adam算法能够快速收敛,解决局部最优问题,适用于比较稀疏的数据集以及训练架构更加复杂的神经网络模型。

2 实验结果与分析

2.1 实验说明

卷积神经网络是一种有监督学习算法,训练样本须是有标签的数据。当变压器出现故障时,由放电位置产生电弧,使得绝缘油分解成CH4、C2H6、C2H4、C2H2以及H2这5种气体,将变压器DGA数据作为网络模型的输入进行故障诊断。根据文献[16]选取5种气体作为特征样本,本文使用的变压器特征气体数据以及对应故障类型均源自文献[17],故障样本数据集组成如表2所示。建立基于Tensorflow2.2.1和Keras2.3的深度学习平台,利用Python3.7.2编写卷积神经网络模型的程序,分别进行基于一维CNN模型和二维CNN模型的变压器故障诊断,并采用不同梯度下降优化算法进行训练,对比分析故障诊断的结果。

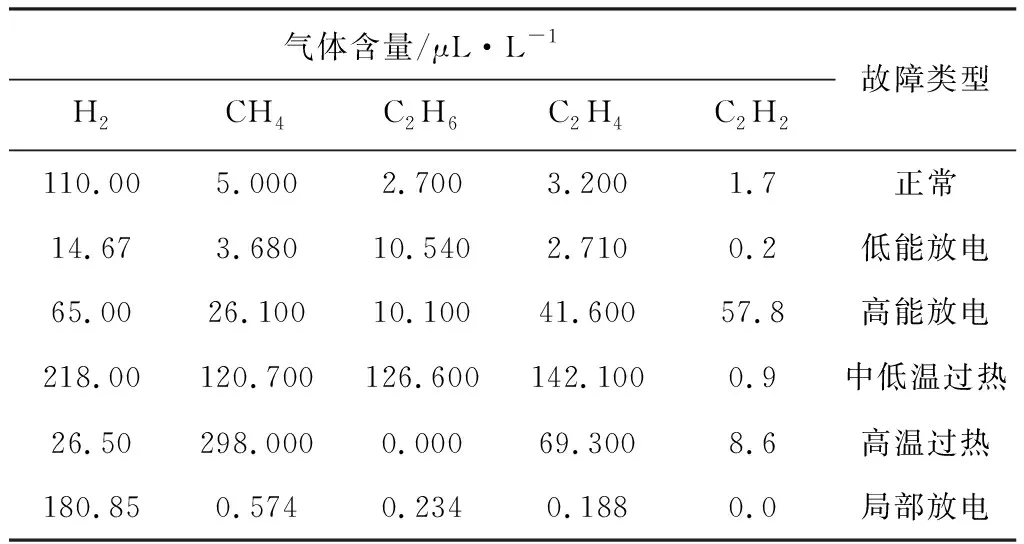
表2 故障样本数据集组成

由于在不同故障类型下产生的5种气体含量不同,按照故障特征可将故障类型分为热故障和放电故障,放电故障包括低能放电、高能放电以及局部放电,热故障包括高温过热、中低温过热,可采用One-Hot编码的方式将其进行分类来区分每一条特征信息,故障类型和对应One-Hot编码如表3所示。

表3 故障类型和对应One-Hot编码

由表3可知,将6个分类存入Tensorflow中,将分类值映射到二进制数,由于本文用于训练的特征变量值较少且各类别相互独立,使用One-Hot编码分类可以提高拟合效果和训练效率。

2.2 一维CNN与二维CNN诊断效果对比

本文选取323条变压器样本数据,其中,正常、低能放电、高能放电、中低温过热以及高温过热、局部放电状态分别为44、39、43、120、42和35条。将数据集分别以6∶4、7∶3和8∶2的比例建立相对应的训练集R1、R2、R3和测试集T1、T2、T3,进行数据预处理和网络模型搭建,比较一维CNN和二维CNN进行变压器故障诊断的效果,验证二维CNN模型的有效性。一维CNN和二维CNN的诊断准确率对比如表4所示。

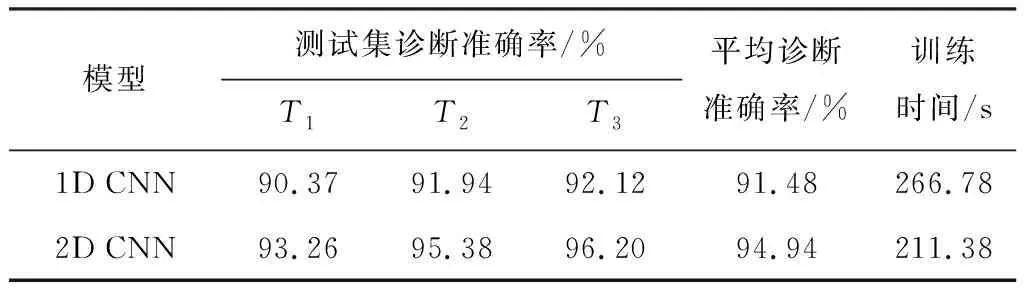
表4 一维CNN与二维CNN诊断准确率对比

一维CNN诊断模型的输入也是变压器油中溶解的5种特征气体。由于各个气体的数量级差别较大,先对其进行归一化,再搭建经典7层LeNet-5神经网络结构。该结构包含了32个卷积核尺寸为3×1的卷积层,32个步长为2的最大池化层,1个全连接层以及Softmax输出层。在特征量较少的情况下,采用Sigmoid和Tahn激活函数容易产生提取梯度迟缓,可能丢失重要特征,因此采用ReLU激活函数可以加速收敛,防止过拟合。

本文提出二维CNN诊断方法对数据维度进行扩充,在保证网络平衡的同时使CNN网络结构可以更高效地提取样本特征。在参数选择时,一维CNN模型中采用3×1的结构,两个卷积核以6个权值为代价,只能获取5×1的感受野。二维CNN结构常用3×3的堆叠卷基层,既可以保证在参数较少的情况下获取更大的感知野,又提升了网络的深度,有效地抑制了过拟合。进行比较实验后由表4可知,传统一维CNN模型不仅参数复杂,而且时间消耗大,诊断准确率也较低,因此一维CNN的性能一般。二维CNN诊断模型在3个不同比例的测试集下均保持了较高的故障诊断准确率,平均准确率达到了94.94%,并且准确率模型参数较少,节约了计算成本,训练时间较短,且在每个测试集上都达到了93%及以上,说明诊断模型的泛化能力较强。其相比传统一维CNN模型精度具有较明显提升,传统一维CNN模型的平均诊断率为91.48%。

基于上述CNN模型与SVM模型[17]进行简要分析对比。

场景1S1:将拓展DGA数据进行特征选择后的5维DGA数据并经过样本预处理后输入SVM模型,进行变压器故障诊断。

场景2S2:将原始DGA数据进行样本预处理后输入二维CNN模型,进行变压器故障诊断。针对以上两个场景,使用50个测试样本,具体训练结果如表5所示。

表5 两种算法准确度对比

由表5可知,原始DGA数据集在CNN模型测试集上的准确度高于SVM,呈现出深度学习模型准确率高于浅层学习模型(SVM)准确率的效果。

2.3 不同梯度优化算法下故障诊断结果对比分析

在训练过程中,迭代步数为1 000次,每批处理的样本个数batch_size为16,在选用10×10大小的二维输入情况下以准确率最终值为指标,依次使用3种神经网络优化器进行故障诊断,各个优化算法参数如表6所示。本文取学习率lr为0.01,β为衰减率,β1、β2为一阶、二阶矩估计衰减值,ε为最终收敛误差值。

表6 不同优化算法参数表

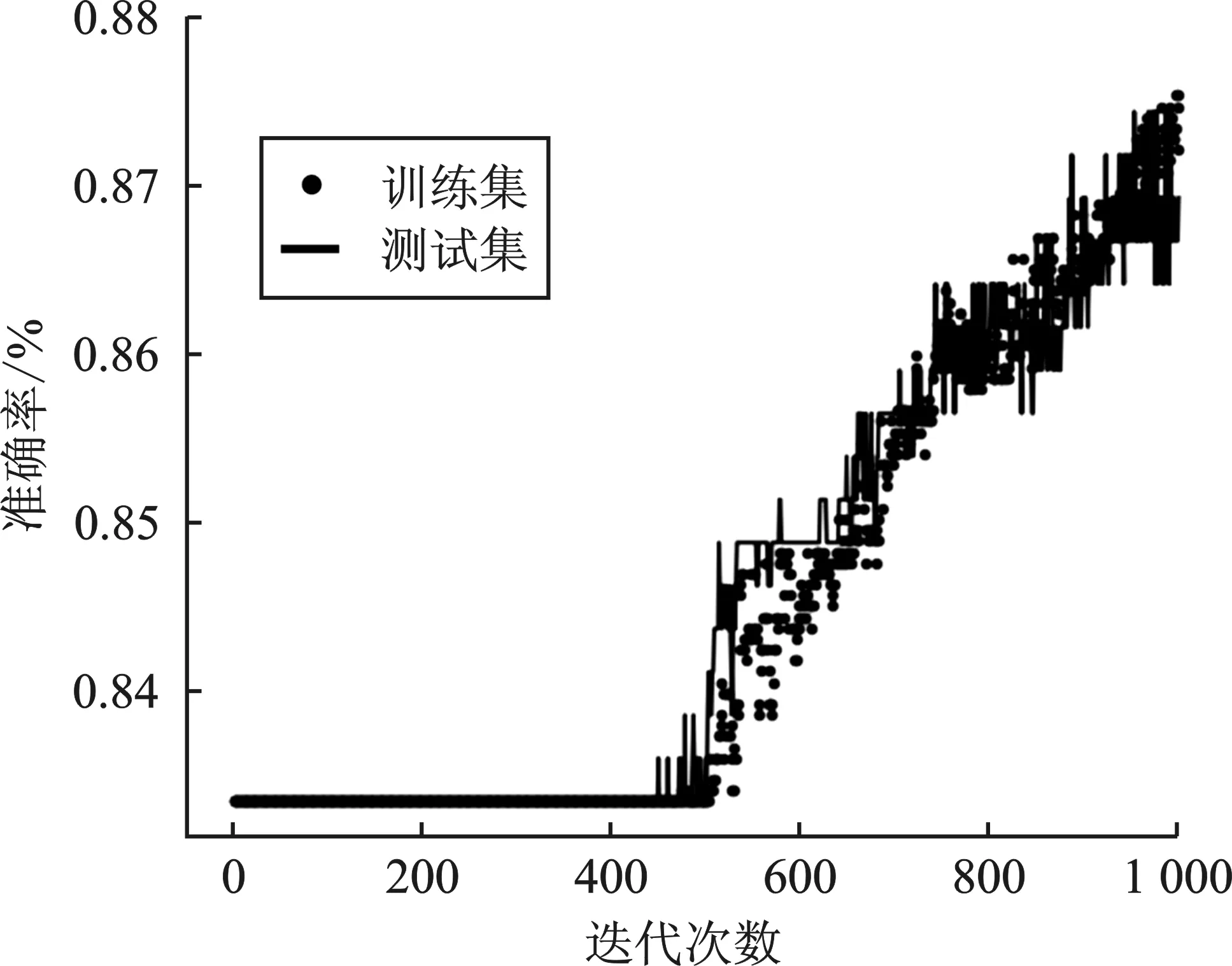
使用3种梯度优化算法对CNN模型进行优化后的诊断结果如图4所示。

(a)

由图4可知,SGD算法识别精度较低,在训练过程中发生震荡,在迭代次数为500次之前训练难以收敛到极小值,可能被困在鞍点,准确率一直在某个值附近。随着迭代次数增多,诊断准确率开始增长,在迭代次数达到1 000次时仍然有震荡现象产生,诊断效果不佳。在使用RMSprop优化算法的训练过程中,准确率随着迭代次数的增大而增高,相较于SGD算法比较平稳但也有小幅度地波动。传统的Adam优化算法在迭代次数为200次时能够较快地进行收敛并且能稳定在95%附近,训练的模型拟合性较好,未发生震荡,兼顾了训练的精度和平稳性。经过改进后的Adam优化算法在迭代次数为300次时突然发生震荡,但最后随着迭代次数的增加,训练过程趋于平稳,最后收敛于一个较小的训练误差,实现了较高的训练精度。由图5可知,改进后的Adam算法准确率优于其他3种算法,并且随着迭代次数的增加,准确率明显提高。

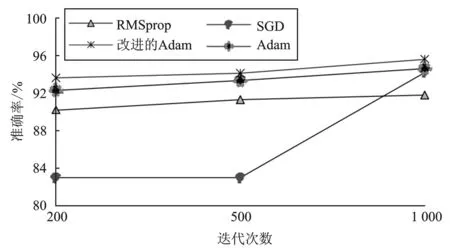
图5 不同优化算法下的诊断准确率对比Figure 5. Comparison of diagnostic accuracy under different optimization algorithms

在迭代步数1 000次的情况下,3种不同的优化算法下训练时间和诊断精度的对比如表7所示。

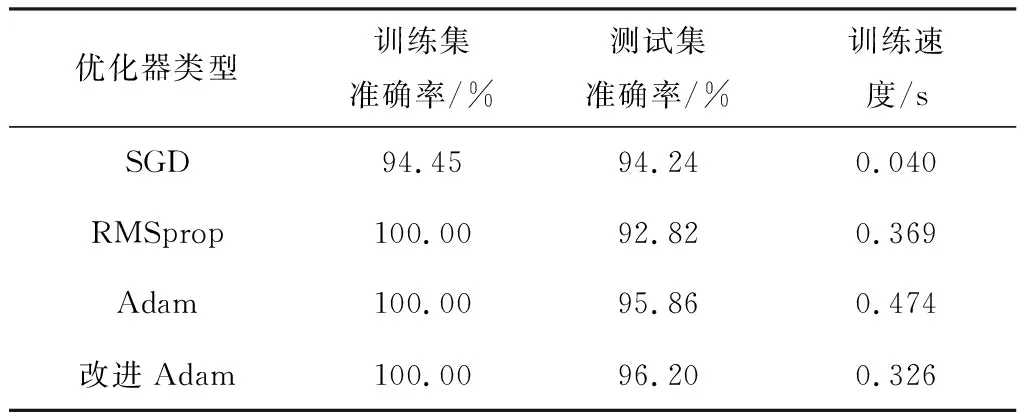
表7 不同优化算法下的综合性能对比

由表7可知,除了SGD优化算法,其他3种优化方法的训练集准确率都达到了100%,说明SGD算法识别精度较低,会发生震荡使极小值被困在鞍点,准确率一直保持在94.0%附近。随着迭代次数增加,准确率增长到94.2%,诊断效果较差。但是该算法每次迭代只使用一个样本,训练速度低至每批次0.04 s。RMSprop优化算法迭代初期的训练过程不稳定,收敛误差较大,最终得到的模型训练精度仅为92.82%

经过改进的Adam算法存储了过去梯度的平方Vt的指数衰减平均值,并且保留了了过去梯度Mt的指数衰减平均值,比RMSprop和传统Adam算法的效果更好,并且在Tensorflow环境中训练时是一个不断寻找最优参数的过程,Adam的分布式计算可以大幅节约时间,完成高效、高质量的训练。从表7可看出,改进后的Adam优化算法可以兼顾收敛性、训练速度和训练精度,准确率高达96.2%,同时也证明了模型的泛化能力较强、稳定性良好。

2.4 学习率和Dropout比率对诊断准确率的影响

Dropout层可以有效地缓解过拟合现象,能够达到正则化的效果[18],在模型全连接层之前加入Dropout层可以有效地优化模型性能。在实验中发现Adam优化算法的学习率和Dropout比率会影响变压器故障诊断结果,如图6所示。

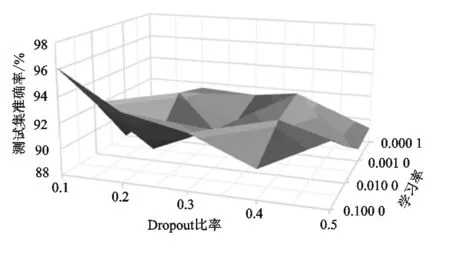
图6 学习率和Dropout比率对诊断准确率的影响Figure 6. Impact of learning rate and Dropout rate on diagnostic accuracy

从图6可以看出,当Dropout比率为0.1时,诊断的准确率最高,当学习率分别被设置为0.1000、0.0100、0.0010、0.000 1时,诊断结果准确率随着学习率的减小而降低,设置较小的学习率导致损失下降过慢,而设置较大的学习率会有更快的初始学习。实验结果表明,当学习率和Dropout值选择合适时,模型并不会发生过拟合现象,证明了基于改进Adam优化算法的二维卷积神经网络模型能够有效防止过拟合,同时合理设置Dropout比率参数增强了模型的稳定性。

3 结束语

针对基于传统一维卷积神经网络的故障诊断方法由于样本特征量不足导致模型诊断性能较差问题,本文采用二维卷积神经网络方法对油浸式变压器进行故障诊断。通过数据增强方法将原始一维时间序列数据转换为二维图片,使用在图像识别领域应用广泛的二维卷积神经网络模型进行训练。将该方法与改进的Adam算法相结合,比较了3种不同的梯度下降方法在训练效果和分类精度上的差异,得出如下两点结论:

1)本文所得方法采用数据增强技术,在保留了原始数据特征的前提下得到相对平衡的二维数据,相较于传统的一维CNN方法具有更高的诊断准确率。

2)实验结果表明,本文使用的自适应优化算法能够减少震荡,使训练过程比较平稳,提高了网络的收敛速度和泛化能力,能更快地达到较高的识别准确率。