基于EMD-Bayes-SVR组合模型的短期电力负荷预测

王雨前,王万雄

(甘肃农业大学 理学院,甘肃 兰州 730070)

电力负荷预测是电网调度人员合理规划发电计划的主要依据,精确的负荷预测可以使系统发电量与负荷尽量达到动态平衡从而提高系统运行效率、降低发电成本。电力负荷预测主要分为长期预测、中期预测、短期预测以及超短期预测。大部分电力公司希望以小时作为次日风电预测尺度[1],因此选择小时作为预测单位进行短期电力负荷预测是合理的。

电力负荷预测方法目前分为3大类:传统统计学预测、机器学习预测和组合模型预测。传统统计学预测主要有时间序列预测[2]和回归预测[3]等。在时间序列预测中自回归积分滑动平均模型[4]最为经典,该方法充分利用了电力负荷序列的时序性,但电力负荷序列受气候、节日、工作日等因素影响变得不平稳时易导致模型失效。回归预测方法模型原理简单,计算过程简洁,但对于线性不可分数据难以取得较高的预测精度。在传统统计学预测方法中,高频分量难以预测,所以为了降低高频分量产生的误差,经常对电力负荷序列进行模态分解。机器学习模型包括BP(Back Propagation)神经网络[5-6]、支持向量回归(SVR)[7-12]和随机森林[13]等模型。BP神经网络具有传统统计学模型少有的学习能力和多元映射能力,因此能够在非线性数据集上取得较好的预测精度。支持向量机可处理非线性不可分数据,因此也适用于电力负荷数据。但机器学习模型的缺点在于其预测精度取决于数据量的大小和数据集的完整性,并且机器学习模型中超参数的调整对模型的预测精度具有直接影响。鉴于传统统计学预测模型和机器学习预测模型都存在自身的局限性,故组合模型应际而生。组合模型预测旨在将不同单一模型的优势组合在一起,从而降低预测误差,提升模型的泛化能力,但组合模型在单一模型的选择上必须注重模型的可解释性。

电力负荷数据根据时段、季节和工作日等因素实时变化,其序列具有非线性、不平稳和随机性等特点,而经验模态分解(EMD)[14-16]是自适应的信号时频处理方法,适用于处理非线性、不平稳数据。将数据去噪方法和数据驱动模型结合起来可以提升预测精度,且支持向量回归机在非线性数据集上泛化错误率低,其结果具有较好的推广性,因此考虑结合这两种方法的优势建立组合模型。贝叶斯优化(Bayesian Optimization)算法[17-18]能以较少的步数和计算过程找到最优的超参数组合,因此本文选用该算法对SVR模型的参数c和g进行调优,提出EMD-Bayes-SVR组合预测模型。由于EMD-Bayes-SVR模型充分考虑了EMD方法、SVR模型以及贝叶斯优化算法各自的优势,因此基于该模型的性能以及可解释性,也可将此模型应用于非线性且不平稳的时间序列预测中,例如股票价格预测、风速预测和降雨量预测等领域。为了突出EMD-Bayes-SVR模型预测的优良性,选择多元线性回归模型(Linear Regression,LR)、随机森林模型(Random Forest,RF)、极致梯度提升(Extreme Gradient Boosting,XGBoost)、梯度提升树(Gradient Boosting Decision Tree,GBDT)、轻度梯度提升机(Light Gradient Boosting Machine,LightGBM)、自适应提升算法(Adaptive Boosting,Adaboost)、BP神经网络和SVR这8种单一预测模型以及EMD-LR、EMD-Bayes-RF、EMD-Bayes-XGBoost、EMD-BP、EMD-Bayes-GBDT、EMD-Bayes-lightGBM、EMD-Bayes-Adaboost共7种组合预测模型作为参照模型。

1 基本理论

1.1 EMD

经验模态分解基于其自身的时间尺度规律进行分解,该方法在分解前无需给定基函数,所以该方法在原理上几乎适用于大部分的信号分解。将原始电力负荷序列经过经验模态分解为若干个相互独立的本征模函数(IMF)和一个残差项(Res)。不同IMF代表了不同时间尺度上的阶段特征,其在充分利用数据所蕴含的信息的同时又避免了局部特征间的干扰,每个IMF需要满足一定条件:

1)在整个数据集上,原始负荷序列中所有的极值点个数与X轴交点个数的绝对值之差小于等于1;

2)在原始信号的任意时间点,上、下包络线以时间轴为对称轴。

给定原始信号X(t),EMD方法的流程为:

步骤1找出原始信号的所有极值点,所有极大值点相连形成上包络线Un,所有极小值点相连形成下包络线Ln;

步骤2计算上、下包络线的均值m1=(Un+Ln)/2,画出均值包络线;

步骤5一个IMF分量的产生需要反复迭代多次,在计算得到第1个IMF1后,通过步骤3计算中间信号作为新的原始信号,然后重复上述步骤得到IMF2,以此类推,直至所有IMF全部分解完成。

式中,L[y,f(x)]为ε损失函数,且损失在预测偏差小于ε时为0。

步骤4判断h1是否满足IMF条件,若满足,该信号即为第一个IMF分量;若不满足,则以该信号为基础,重复步骤1～步骤4;

2.全民健身休闲设施条件得以改善。2016年，广西筹措169亿元用于全民健身工程项目建设，重点支持建设18个县级体育场馆、41个街道（社区）全民健身广场暨街道（社区）多功能运动场、72个乡镇全民健身广场暨乡镇农民体育健身工程、80条全民健身路径和371个2016年度“脱贫摘帽”贫困村村级农民体育健身工程等体育惠民设施。

EMD分解流程如图1所示。

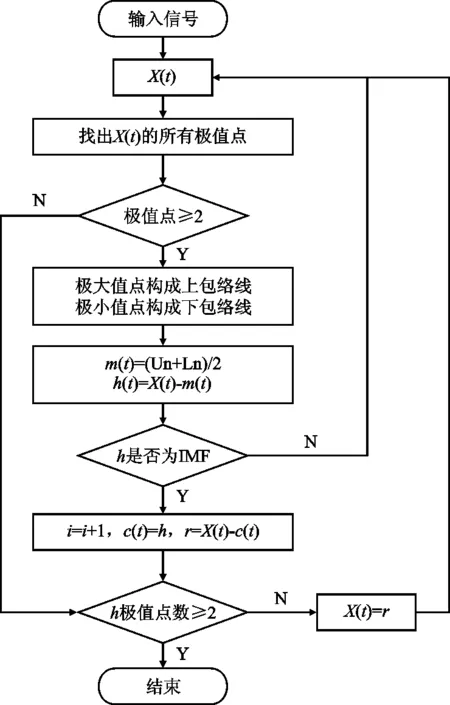
图1 EMD分解流程Figure 1. EMD decomposition flow

1.2 赫斯特指数的基本理论

基于重标极差(R/S)分析方法的赫斯特指数(Hurst exponent,H)是判断时间序列数据遵从随机游走还是有偏的随机游走过程的指标,其反映了一长串相互联系事件的结果。该指数的取值范围为0～1,当H=1/2时,时间序列无相关性;当H>1/2时,时间序列具有长记忆性;当H<1/2时,时间序列的波动强于纯随机序列,即序列表现出反持续性,其计算方法如下:

取一个IMF1(t),t=1,2,…,对于任意正整数τ≥1,τ=1,2,…,n,其序列均值、累积差、极差、标准差和R/S计算式如式(1)～式(5)所示。

幼儿园开展一日活动已经是当前社会发展的必然趋势，幼儿教育的这种改革已经引起各界人士的重视。一日活动主要是为了使课程的难度、知识点与幼儿的智力、接受知识的方式之间严密契合。在幼儿园的教学过程中，将课程引入游戏、运动、生活中可以使幼儿的学习变得轻松，进而提高幼儿的学习效率，使幼儿能够轻松愉快的学习并成长。

(1)

(2)

R(t)=maxX(t,τ)-minX(t,τ)

(3)

(4)

(5)

1.3 贝叶斯优化算法

贝叶斯优化算法在参数优化过程中应用高斯过程,即通过不断增加样本点来更新优化对象的后验分布,直到其函数的后验分布无限逼近于真实分布。贝叶斯优化算法在参数寻优过程中充分考虑到上次参数的信息来实现对目标函数的学习,其迭代次数少、速度快、在参数较多的时候也不会出现维度爆炸等问题,即使在处理非凸问题时依然稳健。

算法流程为:

步骤1输入f、x、δ、M。其中,f为黑箱函数,x为参数搜索空间,δ为采集函数,M为所建立的高斯模型;

步骤2初始化数据集D;

步骤3将所选参数循环迭代T次;

步骤4转换为凸二次规划问题并求解

步骤5通过采集函数计算下一个评估点,将所得评估点汇集为一组超参数{x1,…,xi},其中y=f(x);

步骤6将超参数带入贝叶斯网络进行训练,得到最大目标函数,最后输出yi。

贝叶斯优化算法流程如图2所示。

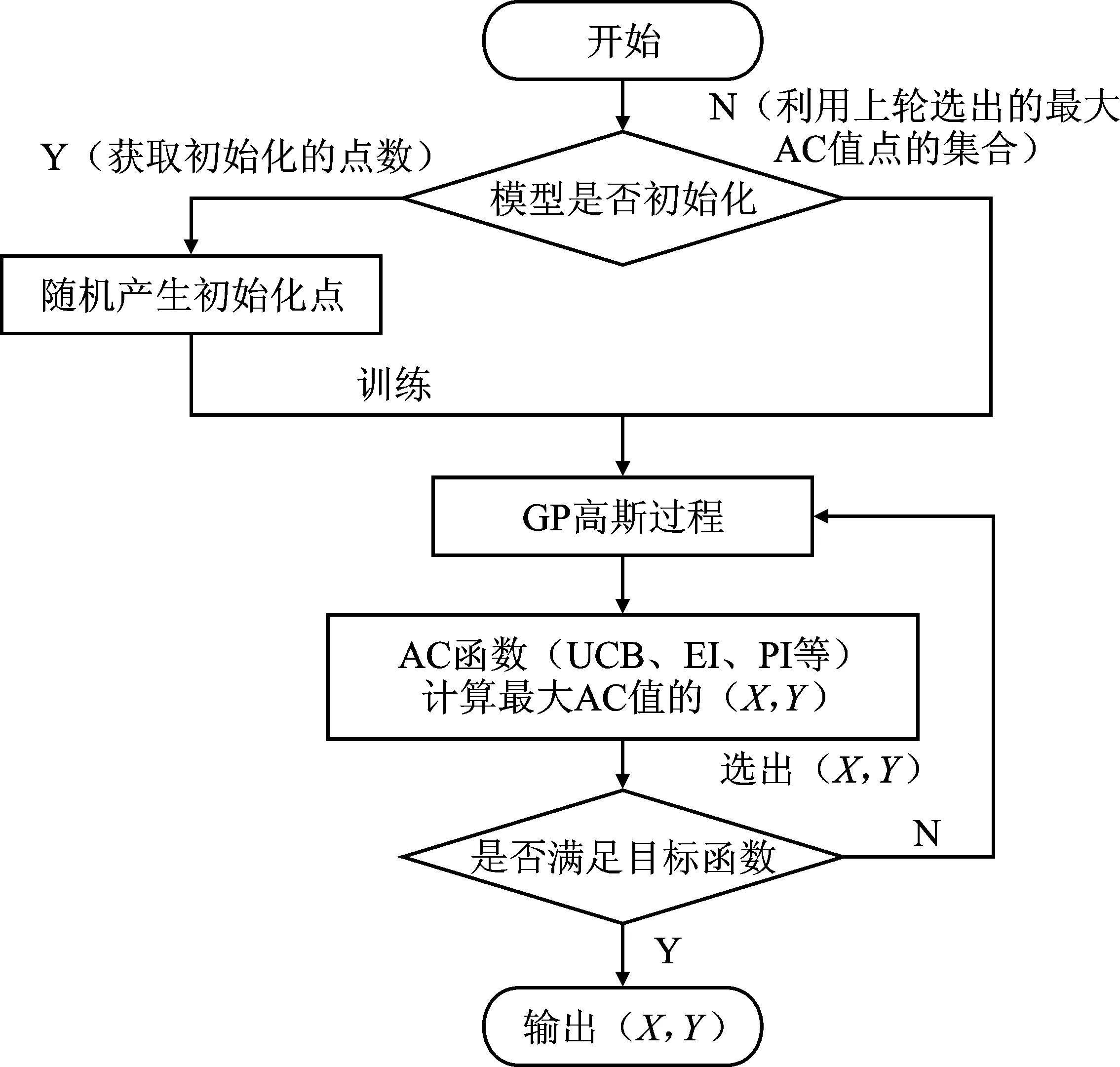
图2 贝叶斯优化算法流程Figure 2. Bayesian optimization algorithm flow

1.4 SVR的基本理论

SVR是支持向量机(Support Vector Machines,SVM)的分支,SVM保证了距离分离超平面最近的点与分离超平面之间的距离最大,而SVR保证了距离分离超平面最远的样本点到分离超平面的距离最小,其算法流程为:

步骤1假设样本S={(xi,yi)},i=1,2,…,n。其中,xi为输入;yi为输出。

元和二年十二月,史官李吉甫等撰《元和国计簿》十卷,总计天下方镇,凡四十八道,管州府二百九十三,县一千四百五十三,见定户二百四十四万二百五十四。其凤翔、鄜坊、邠宁、振武、泾原、银夏、灵盐、河东、易定、魏博、镇冀、范阳、沧景、淮西、淄青十五道七十一州,并不申户口数。每岁县赋入倚办,止于浙西、浙东、宣歙、淮南、江西、鄂岳、福建、湖南等道,合四十州,一百四十四万户,比量天宝供税之户,四分有一。[注]王溥:《唐会要》卷84,北京:中华书局,1955年,第1552-1553页。

步骤2将低维特征空间映射到高维,定义一个核函数K(s,t)和非线性转换函数φ(x),使得φ(xj)

f(x)=ωTφ(x)+b

(6)

式中,ω为权值系数;b为偏执项。

假设一训练的输入向量为 X=（x1，x2，x3，…，xn）T，期望输出为 Y= （y1，y2，y3，…，yn）T，实际输出为 Y′=（y1′，y2′，y3′，…，yn′）T。

步骤3鉴于在做回归预测时无法避免偏差,所以引入不敏感损失函数

L[y,f(x)]=max{0,|y-f(x)-ε|}

(7)

步骤3计算中间信号,即计算原始信号x(t)与均值包络线m1的差h1=X(t)-m1;

步骤4通过已知数据集D和预先假设M服从高斯分布的信息计算模型的函数计算式;

(8)

(9)

步骤5将高频分量、低频分量和残差分量的预测结果相加得到最终的预测值;

步骤5得到SVR的估计计算式

(10)

式中,∂i和∂i*为拉格朗日乘数。

2 实证分析

2.1 数据采集及分析

本文所有数据均来自美国国家航空和宇宙航空局(NASA,http://www.eia.doe.gov)网站发布的内布拉斯加州的历史电力负荷数据。在小数据量小特征情况下,简单的多元线性回归模型即可还原真实的数据趋势。在大数据量小特征情况下,机器学习模型例如集成的树模型预测效果优于深度学习模型。随着数据量和特征数不断增大,机器学习与深度学习模型的表现趋于接近,对模型能力的要求增加而过拟合的风险降低。因此,本文为使所选样本适配于本文所提模型以及参照模型,基于大数据量小特征数截取2020年9月12日～2021年10月30日监测间隔为1小时的共计9 936组数据作为样本进行研究,按照8∶2的比例划分训练集和测试集,并对2021年10月31日的电力负荷数据进行预测,将最终的预测结果与真实电力负荷数据进行比较。由图3所示,电力负荷序列在不同时间点波动幅度不同,且其趋势呈现非线性以及多变特点。因为单一模型较难捕捉到电力负荷数据