基于双重移相的双向有源全桥DC-DC变换器优化控制策略

李玉东,罗新全,李佩峰,黄 鑫

(河南理工大学 电气工程与自动化学院,河南 焦作 454003)

双向有源全桥变换器(Dual Active Bridge,DAB)因具有能量的双向传输、零电压开关以及模块化级联等特点[1-2],在电力电子研究领域备受关注,在分布式微电网系统、储能装置和新能源电动汽车等场合被广泛应用[3-8]。当前对变换器的研究主要集中在移相控制、回流功率以及动态特性等方面。传统单移相控制(Single-Phase-Shift,SPS)在输入、输出电压不匹配时,无法实现全负载范围的软开关,并在功率传输过程中出现较严重的功率回流问题[9]。

为了解决传统移相控制下变换器无法对稳态性能优化的问题,文献[10]在SPS的基础上通过增加原边侧移相角建立双重移相(Dual-Phase-Shift,DPS)控制。相比于SPS控制,该方法增加的一次侧移相角可以有效降低回流功率,但未对变换器的软开关条件进行分析。文献[11]在DPS控制下,重新对内外移相角进行定义并简化了数学模型,减少了自变量移相角之间的耦合度,但未进行具体的回流功率优化算法。文献[12]提出DPS控制下的回流功率优化方法来减少系统的回流功率,但该方法仅在局部情况下分析回流功率最小化情况。文献[13]提出了一种既能够满足软开关条件又能使得变换器回流功率处于最小化的DPS控制策略,但该方法对变压器原副边电压调节变化范围以及功率变化范围具有一定限制。文献[14]提出一种软开关条件下DAB变换器DPS控制的优化方法,该方法能够有效降低开关损耗、降低回流功率并实现软开关的特性。文献[15]提出在全局状况下通过三重移相控制的电流应力优化方法,其中各个工作模式以软开关为前提条件,通过KKT条件函数得到全功率范围内的电流应力最小化方法。该方法能够有效减少电流应力,但闭环调节性能较差且移相比自变量较多使控制情况比较复杂。文献[16]提出了虚拟直接功率的控制策略,但该方法只分析了变换器在SPS控制下的动态响应性能,未考虑变换器在人方法下的稳态效率问题。文献[17]提出环内直接功率-最小电流应力方案,该方案既能提高变换器动态性能又能减少变换器的损耗,但相关参数的引入在降低控制灵活度同时并未考虑最小回流功率特性以及软开关性能。

本文在DPS控制的基础上提出一种虚拟直接功率的回流功率优化方法,简称DPS虚拟直接功率法。该控制策略能够同时实现变换器快速的动态响应和减少回流功率的性能。首先,在分析DPS功率特性的基础之上以软开关为条件,利用KKT条件函数在全局优化条件下实现回流功率的最小化,从而降低变换器的损耗。其次,结合虚拟直接功率法,在保证稳定特性的条件下提高变换器动态响应速度。最后,通过对比实验验证理论分析的正确性。

1 DAB变换器的结构和移相控制工作原理

DAB变换器拓扑结构如图1所示。U1、U2分别为输入端、输出端的电压,C1、C2分别为原副边H桥两端的支撑稳压电容,高频变压器T的变比为n∶1,两边的H桥分别由S1～S4功率开关管、Q1～Q4功率开关管组成,L、iL、uL分别为移相电感、电感电流、电感两端的端电压,uab、ucd分别为原边H1桥的输出电压、副边H2桥的输入电压。

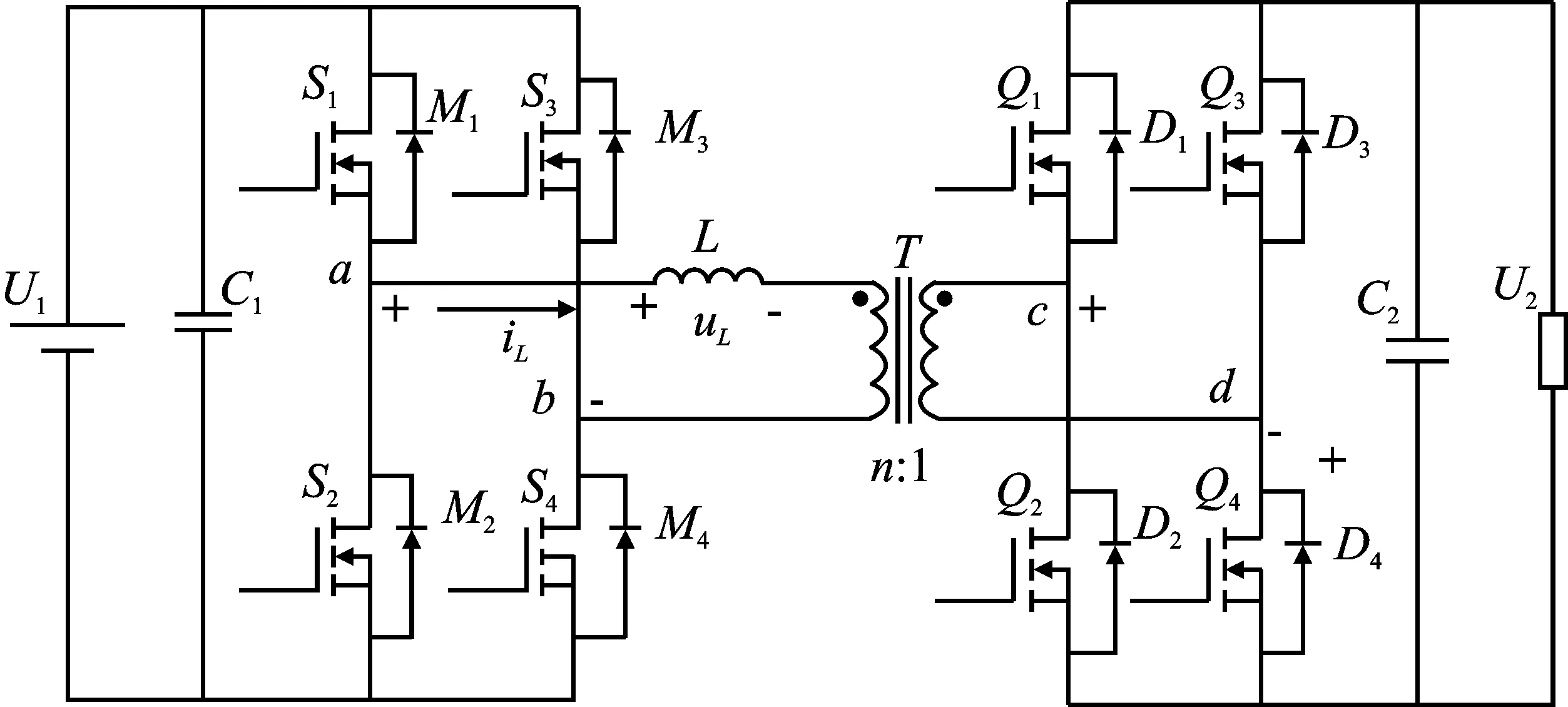
图1 双向全桥DC-DC变换器拓扑Figure 1. Topology of DAB converter

双向变换器在DPS控制下,在能量正向传输过程中,其等效电路及原理波形如图2和图3所示。在图2中,原边H1桥口电压uab为三电平输入电压,副边H2桥口电压ucd为两电平输出电压,电感L对功率传输以及能量存储具有重要作用。在图3中,D1为原边侧内移相比(0≤D1≤1),D2为变压器两侧之间的移相比(0≤D2≤1),且0≤D1≤D2≤1,Th为半个开关周期,Ph1为输入侧传输功率,DPS控制通过控制移相比D来实现功率传递大小以及传递方向。在双重移相控制特殊情况下,当内移相角D1为0时,为传统单移相控制。

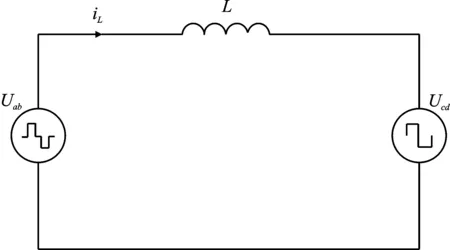
图2 双向全桥DC-DC变换器等效电路Figure 2. Equivalent circuit of DAB converter

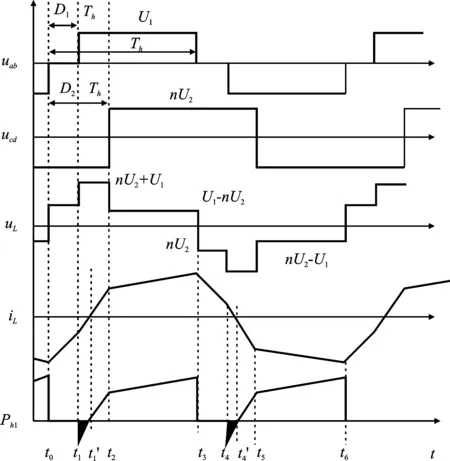
图3 双重移相工作原理波形Figure 3. Waveform of dual phase shift

为方便分析变换器在DPS控制下的工作特性,本文以能量正向传输(0≤D1≤D2≤1)为例分析。在理想工作情况下,根据原理波形图以及电感电流iL周期性的特点[10],推导出电感电流的计算式为

(1)

其中,开关频率f=1/(2Th);电压传输比k=U1/nU2,1≤k。

在DPS控制下,当电感电流iL传递方向与H1桥口电压uab传递方向相反时(t1～t′1、t4～t′4),功率乘积为负,此时间段表明传输功率由一侧流出后又流回,通常将此定义为回流功率。故在DPS控制下,变换器的传输功率P、回流功率Q可分别表示为

(2)

(3)

式中,PN、QN为传输功率和回流功率的基准值。

将式(1)代入式(2),并由式(3)进行标幺化,可得该控制下的传输功率及回流功率计算式为

(4)

由式(4)可绘制在DSP控制下不同k值的回流功率q与D1、D2的关系,如图4所示。在不同电压传输比k值下,均存在移相角D1、D2的组合使得变换器的回流功率得到有效降低甚至为0。

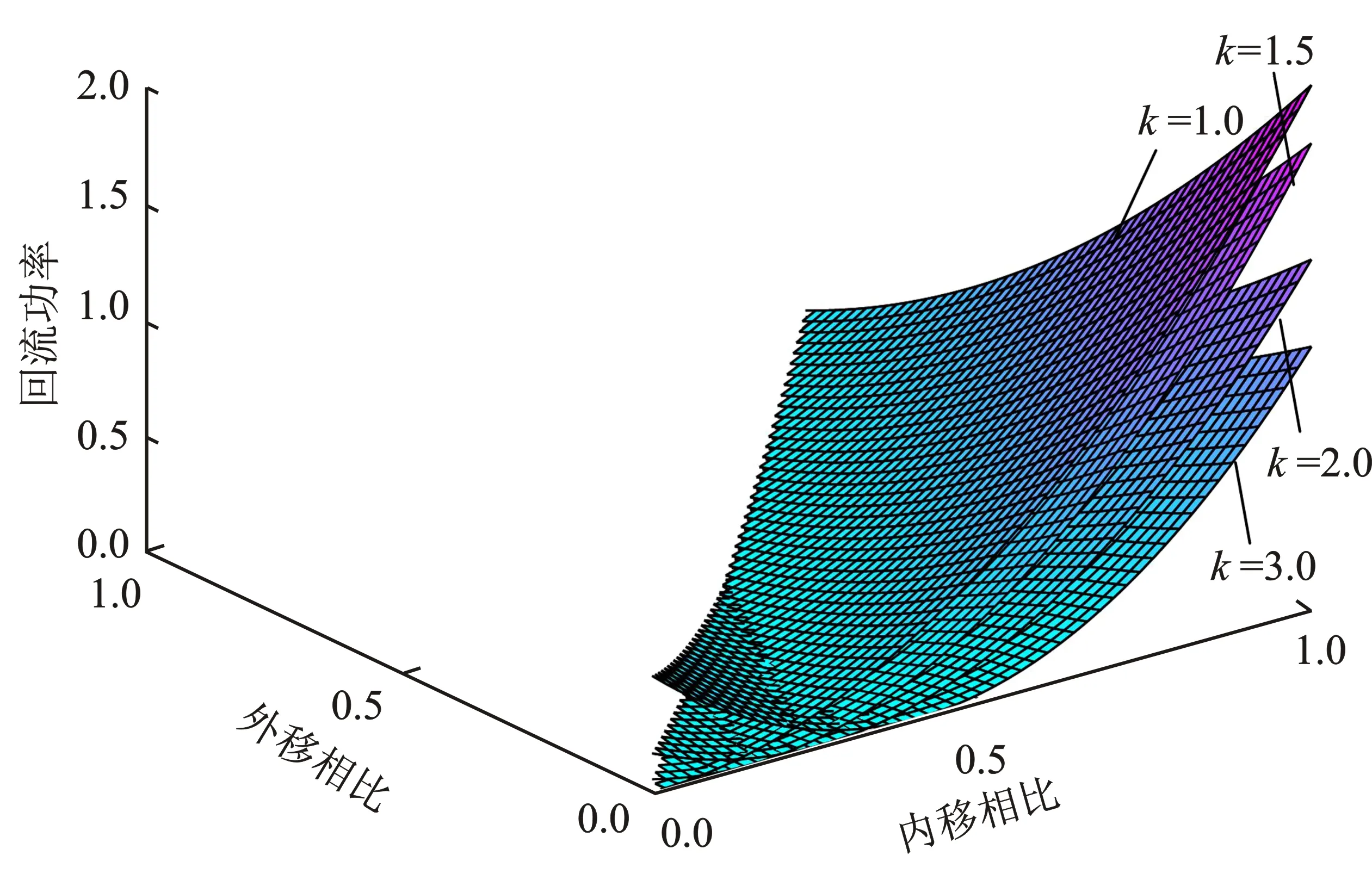
图4 双重移相控制下回流功率q和内外移相比D1、D2、电压传输比k的三维曲线图Figure 4. Three dimensional curves of q、D1、D2 and k under DPS control

2 DPS控制下的优化控制策略

2.1 变换器软开关实现条件

软开关是指开关管通断过程中的电压和电流不在同一时间段内出现,通常是指开关管在开通时刻电压已经为0的零电压开通ZVS(Zero Voltage Switch)。对于DAB变换器来说,当S1、S4、S6和S7的驱动波形上升沿到来时,若电感电流iL<0,此时双向变换器H1桥开关管可实现ZVS特性;当S2、S3、S5和S8驱动波形上升沿到来时,若电感电流iL>0,双向变换器H2桥开关管可实现ZVS特性[14]。根据上述原理,在DPS控制下,以能量正向传输(0≤D1≤D2≤1)为例分析,所有开关管实现软开关的条件为iL(t1)≤0以及0≤iL(t2),其计算式为

(5)

对式(5)进行标幺化处理可得

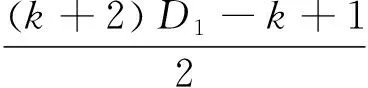
(6)

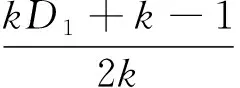
(7)

2.2 变换器回流功率与软开关的双重优化

基于上述分析,由于回流功率过大引起较大功率损耗,使变换器传输效率降低,为此需要对DPS控制下的回流功率进行分析讨论。对于某一传输功率,以回流功率最小化为目标,根据回流功率计算式建立KKT目标函数,并结合等式约束条件的传输功率p以及不等式约束限制条件的移相比关系,则回流功率最小化问题可以表示为

(8)

其中,X(D1,D2)为最优化解集;p*为期望传输功率;Bi(X)为移相角关系形成的不等式限制条件。

根据上述回流功率以及传输功率计算式,该回流功率最小化的KKT条件计算式为

(9)

其中,gi(X)为软开关约束条件和DPS控制下的限制条件(0≤D1≤D2≤1);λ、μi为KKT算子。根据计算式(9)可得回流功率最小化的移相比计算式为

(10)

将式(10)代入式(4)可得最小回流功率为

(11)

将式(10)分别代入DPS控制下的限制条件0≤D1≤D2≤1以及软开关的限制条件中,可得DPS的传输功率范围为

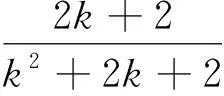
(12)

根据上述求解得到的回流功率最优解以及适用范围可知,变换器的传输功率范围在[0,1]间存在缺失的功率区间。

为满足传输功率的连续性以及回流功率最优化条件,由于回流功率主要由原边侧全桥电路产生,以原边桥开关管的软开关特性为临界条件能够实现双向变换器原边桥输出电流为0,即回流功率为0。其满足的条件为

(13)

由式(13)可得DPS控制实现双重优化的内外移相角的解为

(14)

其解的范围为

(15)

式(15)恰好满足全功率范围的连续性,故变换器在DPS控制下能够在全功率工作范围内实现回流功率的最小化,减少变换器损耗。

2.3 虚拟直接功率法

在DAB变换器工作运行当中,虚拟直接功率控制方法是在变换器的运行状态发生变化时,将得到的传输功率能够快速满足DAB变换器输出功率的需要并建立转换关系,以此来实现变换器快速的动态响应效果。

其传输功率P的定义计算式为

P=U2refi2ref=Uvi2ref

(16)

其中,U2ref为输出电压给定值;i2ref为输出电流给定值。由于输入功率与输出功率给定值之间存在差值,即在变换器工作运行过程中存在的功率损耗问题,因此虚拟输出电压给定值Uv的引入替代了输出电压给定值,能使变换器模型更准确。式(16)中i2ref可定义为

(17)

将式(17)代入式(16)可得

(18)

式中,U2、i2为实时采样的输出电压、输出电流,对式(18)做标幺化处理可得

(19)

由于通过PI控制器得到的虚拟输出电压Uv使变换器在实际运行过程中存在的损耗得到了补偿,故式(19)可简化为

(20)

综上所述,本文提出的DPS虚拟直接功率法的控制结构如图5所示。

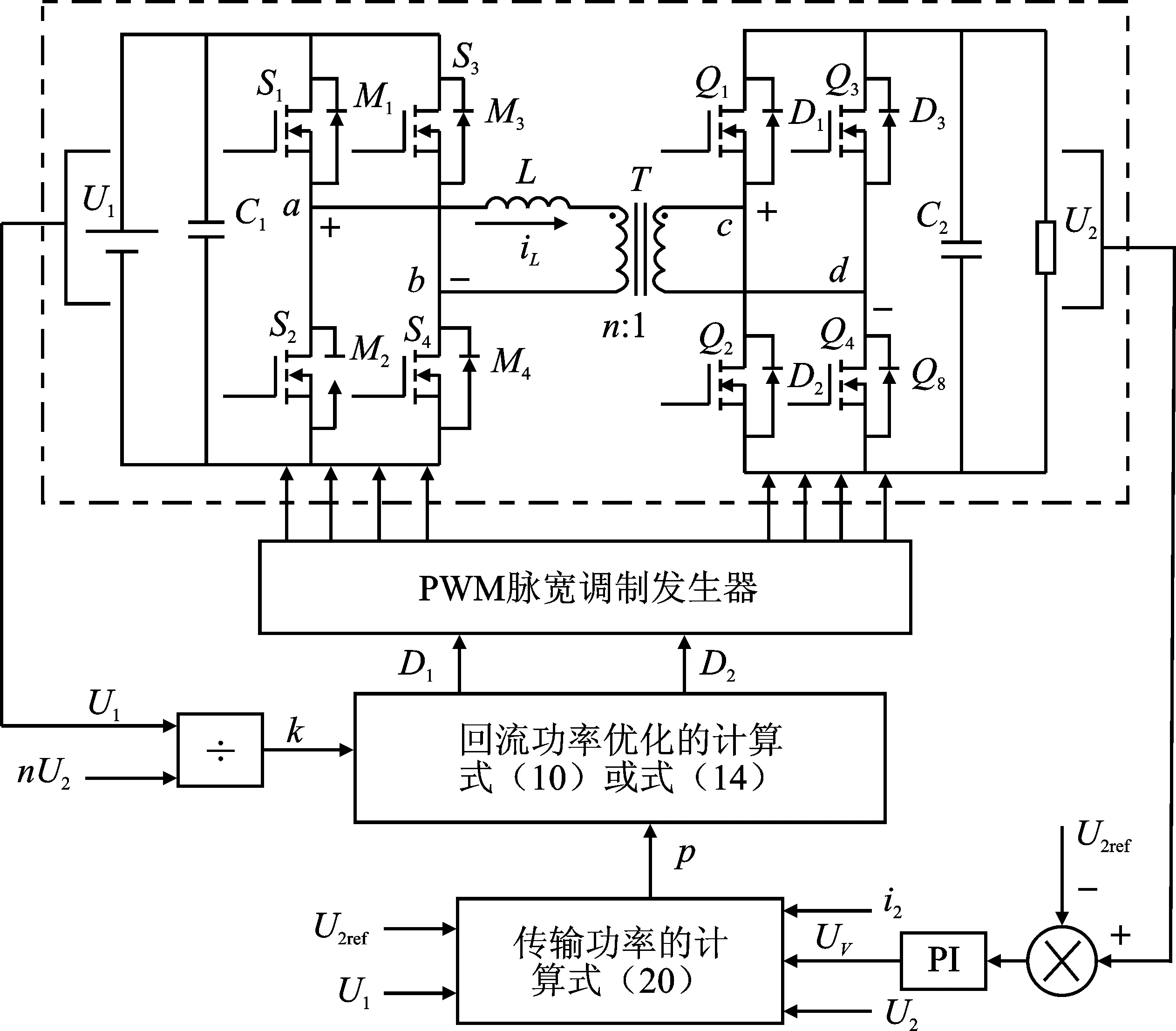
图5 控制结构Figure 5. Control structure

首先,通过采样输入电压U1与输出端电压U2相除得到电压转换比k。其次,由输出端电压U2与参考电压U2ref做差,将差值经过PI控制器得到虚拟输出电压给定值Uv后,根据传输功率计算式可得标幺化的传输功率p,使传输功率与变换器输出端的功率建立转换关系,从而加快DAB变换器的动态响应。最后,由标幺化的传输功率p、电压传输比k确定系统工作的功率范围,并根据式(10)、式(14)求得内外移相比,从而控制相应的变换器主电路开关管通断,实现同时优化回流功率以及动态响应的性能。

3 仿真与分析

为了验证上述控制策略的有效性,在MATLAB/Simulink平台搭建DAB变换器模型,仿真实验平台的相关参数如表1所示,在同等条件下对本文所提优化控制策略与传统移相控制方法进行仿真实验对比与分析。

表1 实验参数

3.1 回流功率优化分析

图6为仿真下的负载电阻R=20 Ω、输入电压U1=100 V时传统单移相控制、DPS虚拟直接功率控制方式下的桥口两端稳态电压波形和桥口一次侧输出的瞬时功率Ph1。由图6可知,SPS控制下存在的回流功率(瞬时功率小于零的部分)较多,DPS控制的优化效果相比SPS控制得到了较大提升,其存在的回流功率为0,证明了DPS虚拟直接功率控制的优越性。

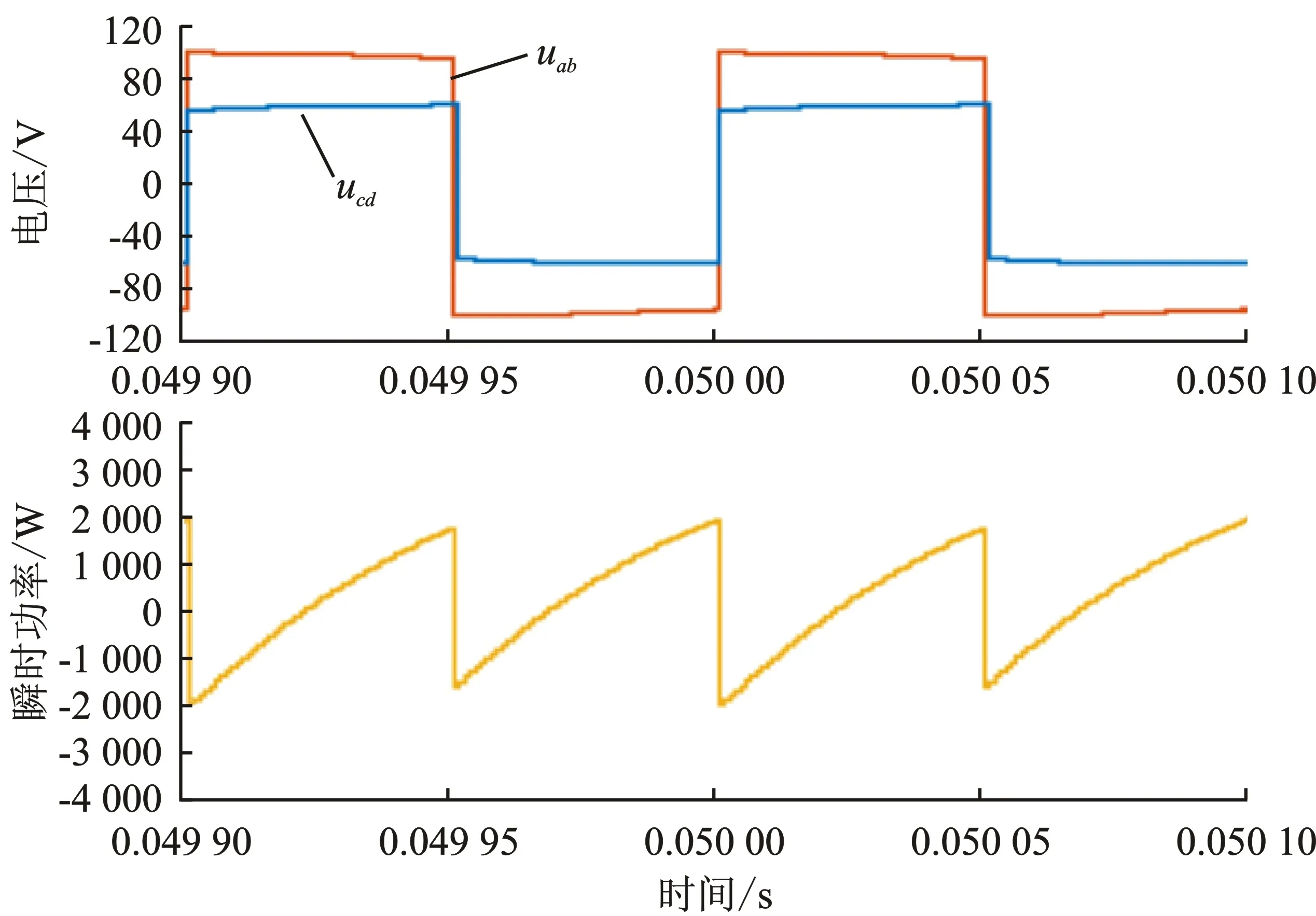
(a)

图7为在DPS控制下,开关管的ZVS状态情况。由于同一桥臂开关管互补导通,故以开关管S1、S3、S5和S7的驱动电压和漏源极电压分析ZVS状态。从图7可看出,在开关管驱动波形上升沿上升之前开关管的漏源极电压已降为0,表明并联在其两端的寄生电容已经结束放电,因此DAB变换器开关管都能实现ZVS。

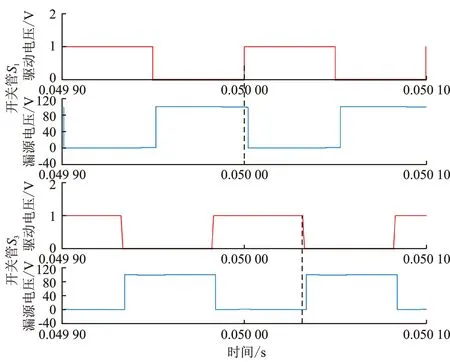
(a)

3.2 动态性能分析

为对比分析两种控制策略下的动态性能,进行了负载突变及输入电压变化时的动态响应仿真实验,如图8和图9所示。

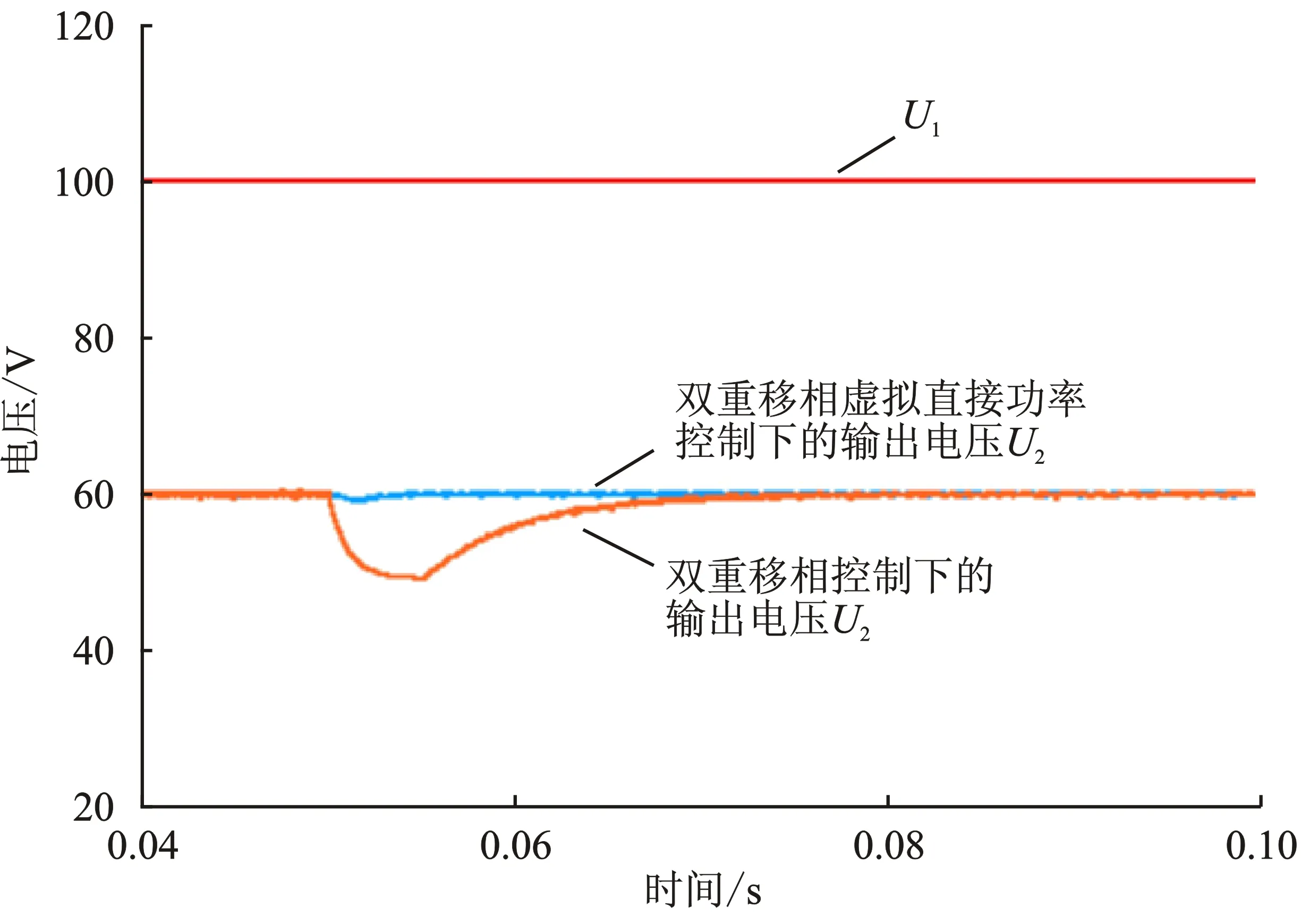
图8 负载突变时电路运行波形Figure 8. Circuit operation waveforms when the load changes

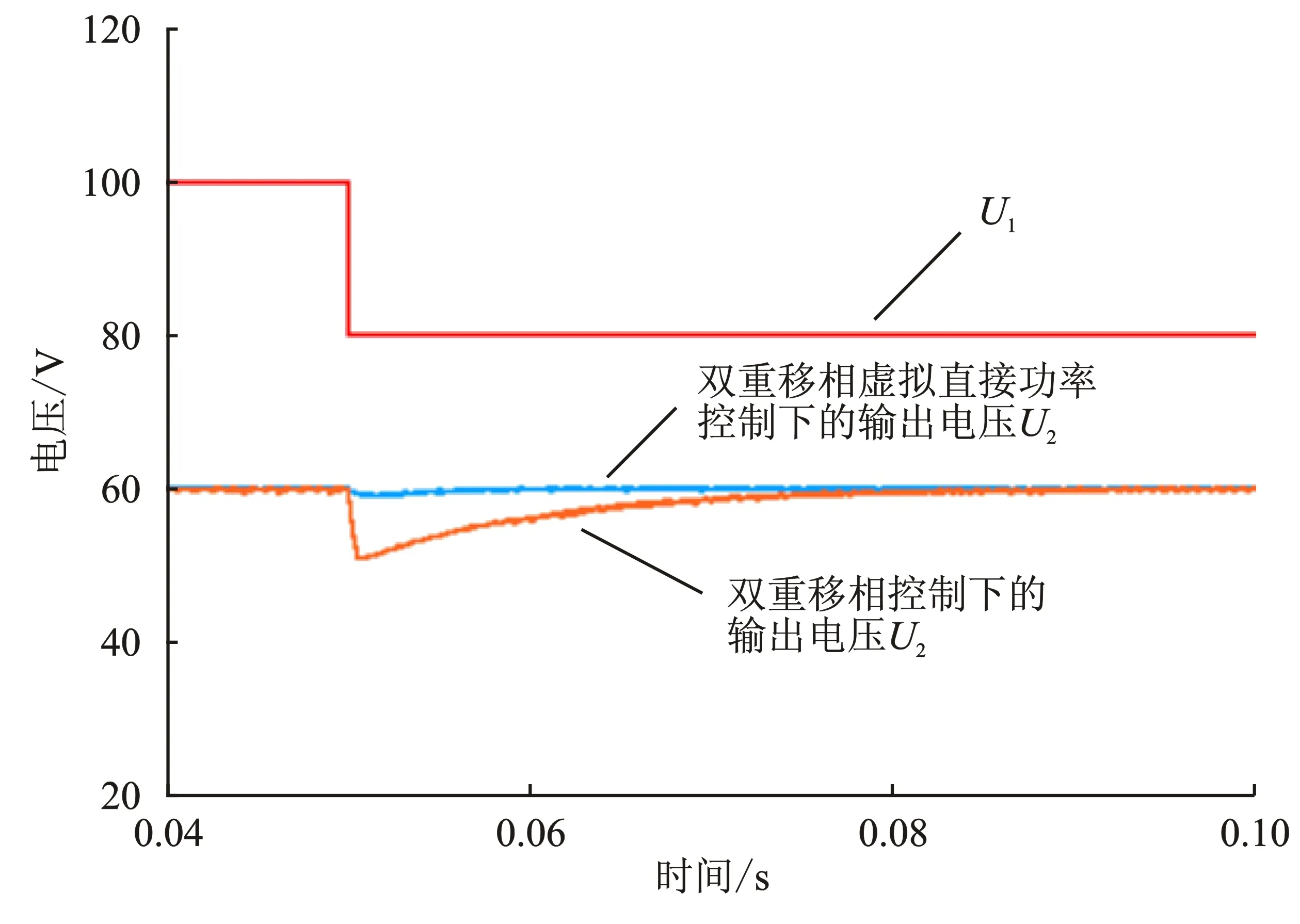
图9 输入电压变化时电路运行波形Figure 9. Circuit operation waveforms when the input voltage changes

图8为负载电阻突变时DPS最小回流功率控制方法与DPS虚拟直接功率控制方案的输出电压运行波形。当负载电阻骤降时,在0.05 s后DPS虚拟直接功率控制下的输出电压波动和调节时间小于DPS回流功率优化控制,具有更好的动态性能。

图9为变换器在相同仿真实验条件下输入电压变化时两方案的运行波形。在输入电压变小时,本文所提DPS虚拟直接功率控制方法下变换器的响应时间比DPS回流功率优化控制下的响应时间更短,表明DPS虚拟直接功率控制方法对输入电压扰动具有更加优良的动态响应特性。

综上所述,本文所提DPS虚拟直接功率控制方法对负载突变、输入电压变化的状况具有较好的动态性能。

4 实验验证

为了进一步验证DPS虚拟直接功率控制方案的可行性,本文搭建以dSPACE-DS1104为核心的半实物仿真平台进行实验验证,如图10所示。实验参数为:输入电压U1为50 V,输出电压U2为30 V,开关频率f为10 kHz,等效电感L为100 μH。实验波形如图11～图13所示。图11为稳态特性时桥口两端电压波形和瞬时功率Ph1,图12为开关管S1、S5软开关特性,图13为负载切换时电压、瞬时功率的变化波形。

图10 dSPACE-DS1104半实物实验系统Figure 10. dSPACE-DS1104 semi-physical experimental system

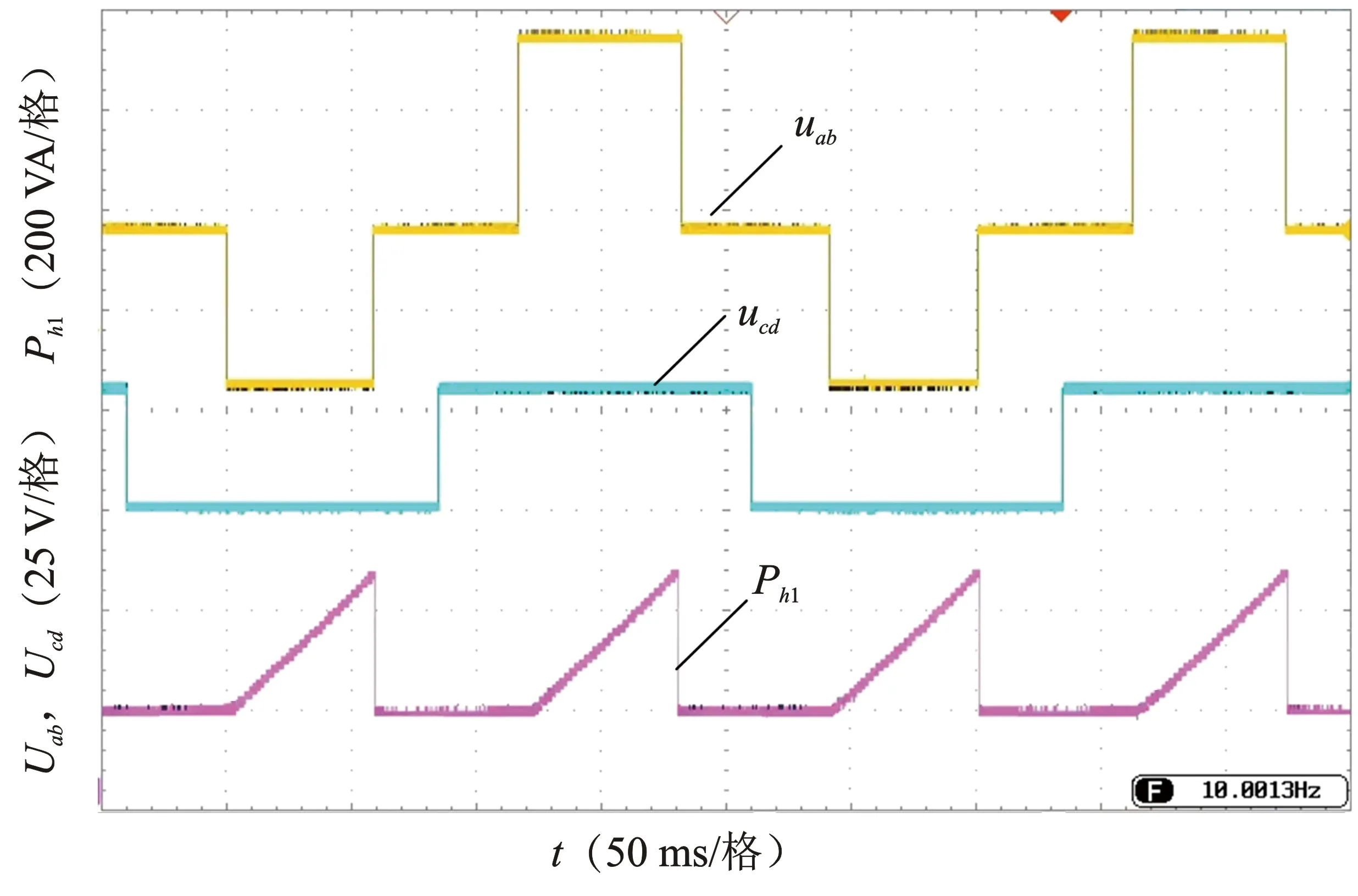
图11 DPS虚拟直接功率控制下电压、瞬时功率实验波形Figure 11. Voltage and inductance current waveforms under DPS virtual direct power control

(a)

从图11可以看出,DPS虚拟直接功率控制方案能实现零回流功率,具有降低损耗的作用。

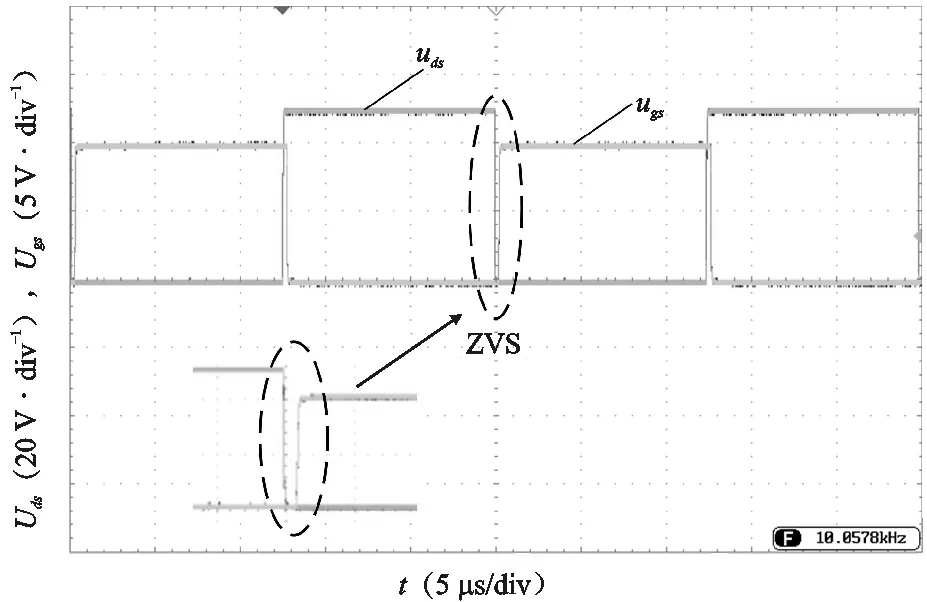
由于变换器同一桥臂开关管互补导通,且原边桥与副边桥对称,选择开关管S1、S5来反应DAB变换器软开关特性。图12表明当开关管的驱动信号Ugs来之前,Uds已经降为0,说明此时开关管均实现 ZVS,与理论仿真分析一致。

由图13可看出,当输入电压为50 V、输出电压为30 V时负载由20 Ω切换到10 Ω工况下,DPS控制下的动态响应时间约为20 ms,本文DPS虚拟直接功率控制方式的动态调节时间几乎为0。

5 结束语

在DPS控制下,本文通过对DPS控制的稳定工作状态的回流功率特性进行分析,以软开关边界为约束条件,利用KKT条件函数求得全功率下回流功率优化方案,该方法使DAB变换器能够有效降低回流功率。同时,通过结合虚拟直接功率方案来提高变换器的动态响应。最后搭建实验平台进行相关对比实验,变换器回流功率优化对比实验验证了DPS虚拟直接功率控制方法能进一步减少DAB变换器的回流功率,并能使开关管实现软开关特性,从而减少变换器的功率损耗。动态性能对比实验表明,DPS虚拟直接功率控制方法的动态响应速度大于DPS回流功率优化控制方法,由此证明DPS虚拟直接功率控制方法能显著优化变换器的整体性能。