基于WGPR的三相不平衡配电网鲁棒状态估计方法

吉兴全，刘小虎，张玉敏，叶平峰，王 飞，任童洲

（1.山东科技大学电气与自动化工程学院，山东青岛 266590；2.国网德州供电公司，山东德州 253073；3.国网铜川供电公司，陕西，铜川 727031）

0 引言

目前，环境问题日益严重，化石燃料日渐枯竭，在国家“双碳”战略目标的背景下，以光伏、风电为代表的分布式电源（Distributed Generator，DG）在配电网中的接入比例不断上升[1-4]。与输电网相比，配电网的三相参数不对称和三相负载不平衡特性是导致配电网状态估计（Distribution Network State Estimation，DNSE）精度不足的原因，当DG 接入后，风、光等一次能源固有的波动性和随机性特点会进一步加剧配电网不平衡，影响DNSE 精度[5]。

随着配电网结构的日益复杂和用户对供电质量要求的不断提高[6-7]，作为配电管理系统重要组成部分的DNSE，其估计结果的精度越来越受重视[8]。由于预测辅助状态估计（Forecasting Aided State Estimation，FASE）可综合负荷和DG 的历史状态数据来获得系统的状态预测值，有效提高数据估计精度，因此在现代能源管理系统中得到广泛应用[9]。

近年来，为了克服标准卡尔曼滤波器（Kalman Filter，KF）不易处理电力系统中量测值和状态值之间的非线性关系问题，众多学者做了大量研究[10-11]。文献[12]为降低量测值中非高斯噪声对FASE 精度的影响，提出基于广义最大混合相关熵的鲁棒无迹卡尔曼滤波（Unscented Kalman Filter，UKF）算法。文献[13]针对量测模型不确定性的影响，提出了自适应的扩展卡尔曼滤波算法，避开了估计误差上限选择困难的问题，提高了估计精度。

由于传统状态估计算法不能充分挖掘电力系统运行数据的深层特征，从而使状态估计的精度受限。与传统算法相比，深度学习算法[14-17]不仅可以有效处理海量信息之间的关系，还可使预测结果更加精确[18]。文献[19]提出基于神经网络的电压暂降估计方法，通过引入区域映射概念提高特征提取能力，但忽略了DG 出力的影响。文献[20]提出一种基于生成对抗网络（Generative Adversarial Network，GAN）的电力系统静态估计模型，可更好地捕捉系统状态的相关性，但该模型未考虑非高斯噪声的影响。文献[19-20]均未计及配电网的三相不平衡特征。

本文针对分布式电源和不平衡负荷接入配电网致DNSE 状态值预测精度不足问题[21]，提出一种基于加权高斯过程回归（Weighted Gaussian Process Regression，WGPR）的三相不平衡配电网鲁棒状态估计方法。本文的创新之处在于：采用卷积神经网络[22-23（]Convolutional Neural Networks，CNN）优化的长短期记忆神经网络（Long Short-term Memory，LSTM）构建CNN-LSTM 预测模型，将状态预测值和高斯回归模型（Gaussian Process Regression，GPR）的状态估计值输入GPR 模型，对状态预测值和状态估计值加权获得最终的状态估计结果。最后，通过对含分布式电源的IEEE34 节点和IEEE123 节点三相不平衡系统的算例分析，验证了本文所提WGPR方法的鲁棒性和精确性。

1 GPR模型

针对量测过程中因信道通信噪声干扰和环境温度变化导致的非高斯噪声问题，本文将FASE 模型[24]改写为：

式中：Xt，Xt-1分别为t，t-1 时刻状态矩阵；Ft为t时刻转移矩阵；gt-1为t-1 时刻状态变化的相关矩阵；wt-1为t-1 时刻过程噪声矩阵；为t时刻含有非高斯噪声的量测矩阵；h-1(·) 为非线性映射函数。

为解决式（2）中传统物理模型难以处理量测值与状态值之间非线性映射关系这一关键问题，引入基于贝叶斯理论的GPR 模型[25]，建立各相节点的量测值和状态值非线性模型，实现FASE 估计。

GPR 模型通过1 组基函数将输入特征映射到高维空间，从而在高维空间寻找数据之间的线性关系。根据Woodbury 恒等式[26]可得GPR 模型表达式为：

式中：p（·）为密度函数；k（·）为核函数；Znew，Zhis分别为新的和历史量测矩阵；Xhis为历史状态矩阵；N（·）为正态分布函数；ψ为基函数；Σ为参数对称矩阵；σ为信号方差矩阵；I为单位矩阵。

GPR 采用置信度判断估计结果，该估计方法可以弱化式（2）中的噪声干扰，从而提高估计结果的精度。GPR 模型结构如图1 所示。

由图1 可知，利用GPR 模型处理非线性问题的优势，可获得量测值和状态值的非线性映射关系。先根据三相不平衡配电网的t时刻之前的量测值zt和状态值xt之间的非线性关系进行离线训练，再将新获得的量测值znew输入模型中，获得经GPR 计算处理得到的状态值xG。

2 加权高斯过程回归模型

为了进一步提高GPR 算法处理非高斯噪声和量测数据异常的能力，本文将CNN-LSTM 和GPR算法集成，将得到的CNN-LSTM 电压预测值和GPR 的状态估计值一起输入GPR 算法中实现加权，最终得到更加精确的状态估计值。

2.1 CNN-LSTM模型

CNN-LSTM 神经网络在时序预测方面具有优势，可有效解决三相不平衡配电网由于量测数据缺失导致的状态估计精度低的问题。CNN-LSTM 模型如图2 所示。

图2 CNN-LSTM模型Fig.2 CNN-LSTM model

CNN-LSTM 模型预测流程为：（1）进行数据预处理，根据配电网和DG 的三相历史运行数据进行潮流计算得到冗余的伪量测值，对得到的各节点的三相量测值进行归一化，并将其划分为训练集和测试集；（2）采用CNN 对预处理后的三相配电网状态值进行细粒度特征[22-23]分析，并将提取的强相关特征传递给LSTM；（3）LSTM 根据提取后的各相状态值特征分别构建时间序列模型，并预测出三相状态估计结果。

2.2 WGPR状态估计算法流程

本文所提WGPR 状态估计算法可利用CNNLSTM 的预测值增强GPR 算法的性能，使状态估计结果更精确。其模型表达式为：

WGPR 状态估计算法流程如图3 所示。

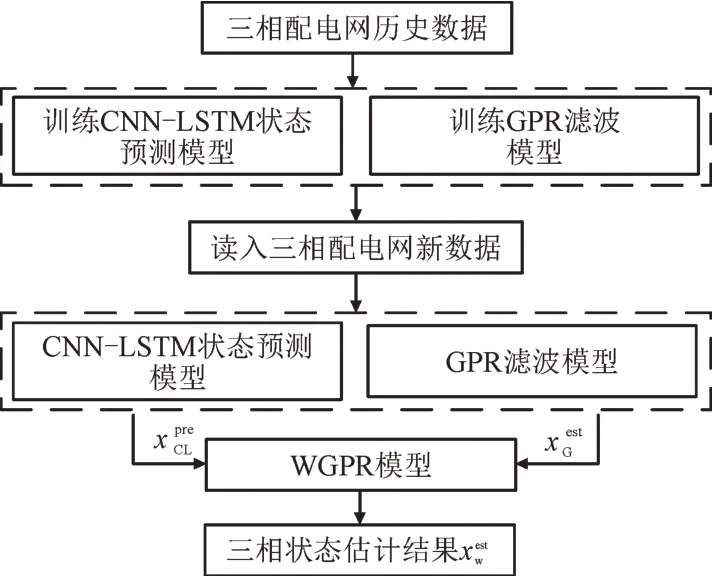
图3 WGPR状态估计算法流程Fig.3 Procedure of state estimation based on WGPR

首先，根据数据库中三相配电网历史数据对CNN-LSTM 预测模型和GPR 滤波模型进行训练；然后，读取三相不平衡配电网量测信息，通过预测模型和滤波模型输出预测值和估计值；最后，将获得的各相预测状态值和滤波结果再次输入WGPR 模型，WGPR 模型则根据输入数据对真实值的影响自行分配权重，继而实现对各相状态值的加权计算，获得最终三相状态估计结果。

3 算例分析

以IEEE 34 节点和IEEE 123 节点三相不平衡配电网为例，验证所提WGPR 算法的有效性。通过OpenDSS 9.4 求解三相潮流方程，获取配电网各相状态数据集和量测数据集，共13 104 组数据。选取80%的数据作为训练集，其余数据作为测试集。在Python3.8 环境中构造CNN-LSTM 和GPR 模型，并通过配电网历史数据完成模型训练。计算机操作系统为Win10 64bit，处理器为Core i5-6300，运行内存8G，显卡为Nvidia GeForce GTX 960M（2GB）。

本文采用平均绝对误差（Mean Absolute Error，MAE）和均方根误差（Root Mean Squared Error，RMSE）反映WGPR 状态估计值和真实值的偏差，其物理量分别用EMA和ERMS表示，所得系统状态数据均进行归一化处理。

3.1 IEEE 34算例系统

含DG 的IEEE 34 节点三相不平衡配电网如图4 所示。

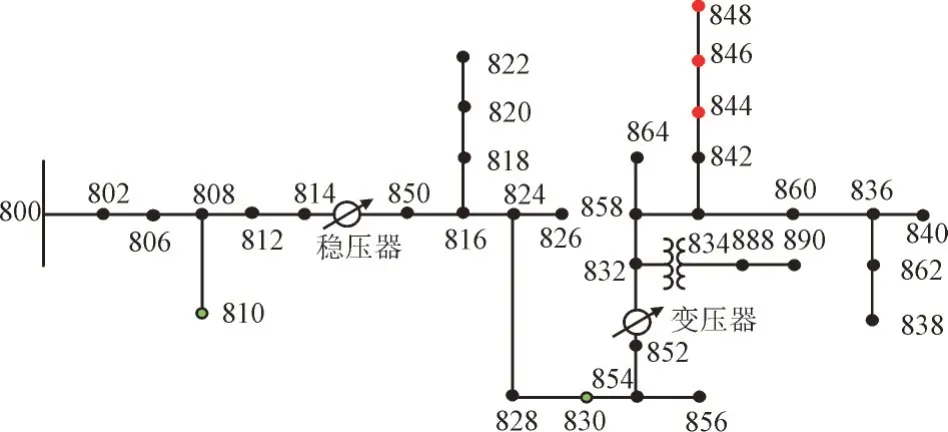
图4 含DG的IEEE 34节点三相不平衡配电网Fig.4 IEEE 34-bus three-phase unbalanced distribution system with DGs

图4 中，在节点800 至节点890 之间的任意34个节点中，随机选择5 个节点作为DG 节点。在绿色节点接入光伏；在红色节点接入风电。

IEEE 34 算例系统DG 属性如表1 所示。

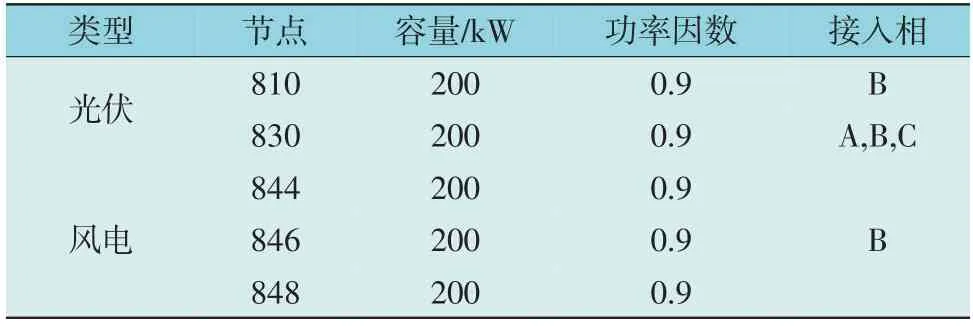
表1 IEEE 34算例系统DG属性Table 1 Attribute table of DG in IEEE 34-bus example system

3.1.1 预测性能分析

为测试所提CNN-LSTM 算法对系统状态预测结果的性能，将其与UKF，LSTM 算法进行对比分析。不同算法下各相节点电压预测结果及参数对比如图5 和表2 所示。

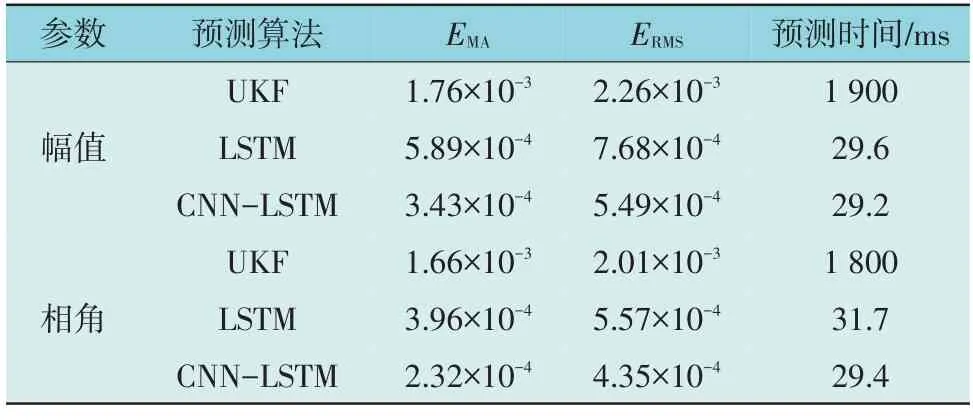
表2 不同算法下电压幅值和相角预测结果对比Table 2 Comparison of prediction results of threephase node voltages among different methods

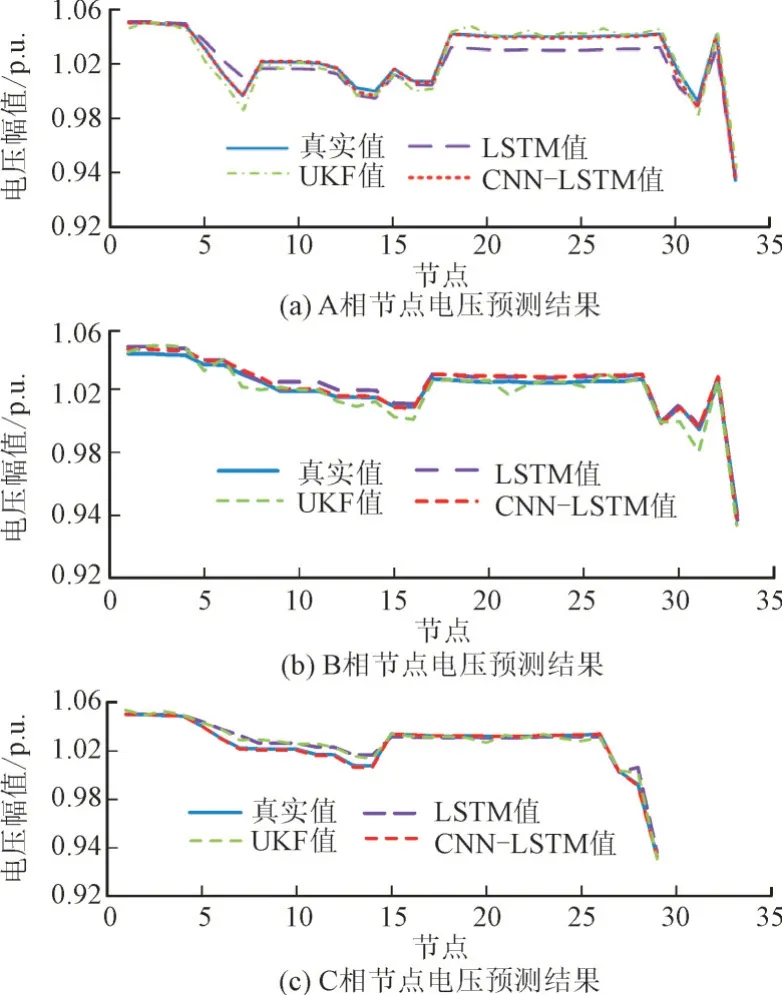
图5 不同算法下各相节点电压预测结果Fig.5 Prediction results of three-phase node voltages with different methods

由图5 和表2 可知，神经网络模型的精度明显高于传统的UKF 算法，而与LSTM 相比，本文所提CNN-LSTM 模型的状态预测值对真实值具有更好的拟合效果。这是由于在三相不平衡系统中LSTM对历史数据特征提取的能力较弱，不易捕捉数据之间的关系，难以挖掘出数据更深层的规律。而CNN与LSTM 相结合可以有效解决特征提取困难的问题，使模型能获得更加精确的状态预测值。同样，在预测时间上，LSTM 和CNN-LSTM 的预测时间均在ms 数量级，明显快于传统的UKF 算法，说明CNN-LSTM 模型在保持较高预测精度的同时能快速输出预测结果。

3.1.2 系统抗噪能力测试

为测试WGPR 算法对于标准差较大的非高斯噪声的处理性能，对量测数据添加标准差为0.01 的拉普拉斯噪声，并与高斯过程回归进行对比，得到节点808 的三相电压幅值在拉普拉斯噪声下滤波结果如表3 所示。

表3 节点808的三相电压幅值在拉普拉斯噪声下滤波结果Table 3 Filtering results of three-phase voltage amplitude of 808 node with Laplace noise

由表3 可知，本文所提WGPR 算法在标准差为0.01 的拉普拉斯噪声环境中，得到的三相滤波结果的EMA和ERMS均保持在10-5数量级以内，与GPR 算法相比，具有更好的抗噪能力。这是因为CNNLSTM 在时序预测时可以直接获得未来的状态值，无需考虑噪声影响；同时，GPR 算法通过核函数将量测值映射到状态值，将低维空间的非线性关系转化为高维空间的线性关系，进而弱化噪声干扰。本文将两种算法的优势结合，得出的WGPR 算法在处理噪声方面更具体。其中节点808 的B 相EMA和ERMS略高于A 相和C 相，原因是B 相接入了单相DG，使得电压的波动更加复杂，在一定程度上影响了估计的精度，但滤波结果依然维持在10-5数量级，由此验证了本文算法在处理噪声方面的优势。

为进一步验证本文所提出的WGPR 滤波算法处理大噪声的能力，以B 相为例依次加入噪声均值为0，标准差分别为0.03，0.05，0.07 的拉普拉斯噪声来模拟数据异常的情况，并与高斯回归过程进行对比。节点808 的B 相电压幅值滤波结果如图6 所示。

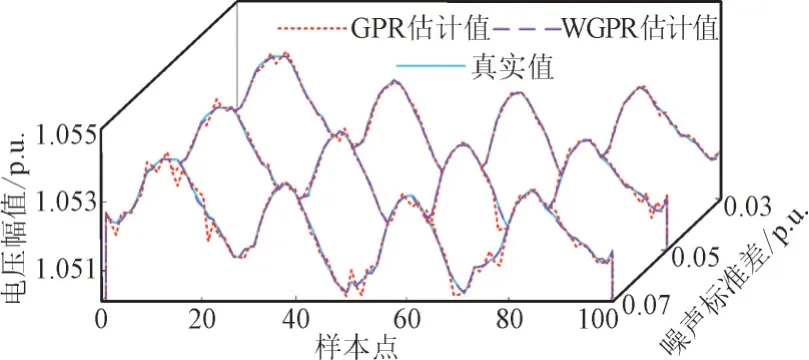
图6 节点808的B相电压幅值滤波结果Fig.6 Filtering results of B-phase voltage amplitude of node 808

由图6 可知，随着噪声标准差的不断增大，2 种滤波算法的滤波效果都受到了不同程度的影响。其中GPR 滤波结果与真实值的偏差明显增大，无法保证滤波结果的精度。而本文提出的WGPR 滤波算法在噪声标准差增大的情况下，仍能保持较高精度的滤波结果。

不同算法的估计性能如表4 所示。

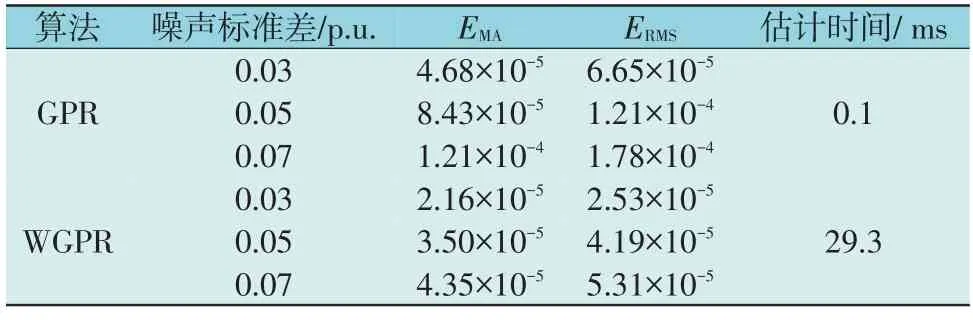
表4 不同算法的估计性能Table 4 Estimation performance of different methods

由表4 可知，随着噪声标准差的逐渐增大，2 种算法的性能差距趋于明显。GPR 算法的EMA和ERMS分别从10-5增加10-4，跨越了一个数量级，变化幅度相对较大；而WGPR 算法在标准差从0.03 逐渐增大到0.07 时，虽然EMA和ERMS数值有所增大，但依旧稳定在10-5数量级以内，这是因为GPR 算法处理数据异常问题的能力有限，而WGPR 在将状态预测值和状态估计值加权处理后，可以自动分配权重，将权重分配得更靠近真实值一侧，最终使得滤波结果更接近真实值。在估计时间方面，由于WGPR 包含GPR 和CNN-LSTM 2 个并行的计算过程，最终计算时间取决于耗时较长的CNN-LSTM 模型，导致WGPR 算法的时效性相比GPR 算法有所降低，但仍维持在ms 数量级，说明本文所提方法在处理标准差较大的非高斯噪声或数据异常时，依然能够在较短时间内获得较为精确的估计结果。

3.1.3 系统鲁棒性测试

假设在样本添加标准差为0.01 的拉普拉斯噪声情况下，样本点为30 时投入DG，样本点为70 时切出DG。以节点890 为例，DG 投入与切出时算法误差绝对值的变化情况如图7 所示。

图7 DG投入与切出时算法误差绝对值的变化情况Fig.7 Change in absolute error of algorithm with and without DG integration

由图7 可知，误差绝对值并没有因为DG 的突然接入出现明显的增大，依旧维持在较为稳定的区间，说明本文提出的WGPR 算法可以较为准确的捕捉量测值和状态值的非线性关系。

为验证DG 接入后算法的稳定性，设置如下4种场景：（1）无DG 接入；（2）只接入风电；（3）只接入光伏；（4）风电和光伏均接入。以节点890 为测试节点，得到不同场景下状态估计性能如表5 所示。

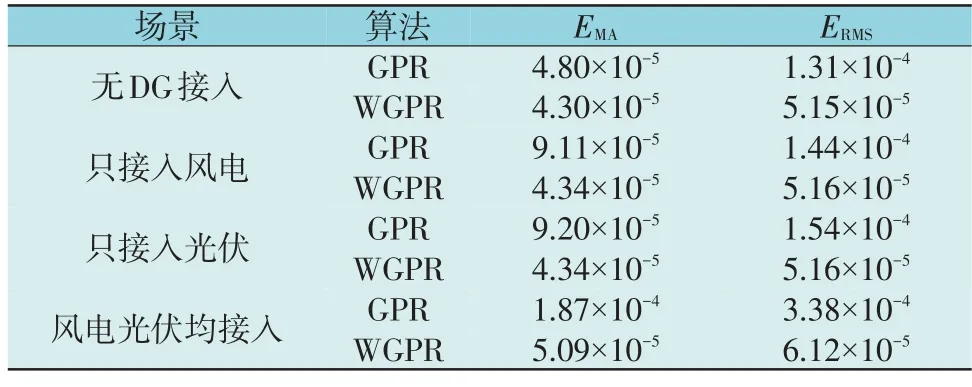
表5 不同场景下状态估计误差Table 5 State estimation errors in different scenarios

由表5 可知，与GPR 算法相比WGPR 算法的EMA和ERMS均维持在10-5数量级，并没有因为光伏或者风电的接入使得估计值明显偏离真实值，说明本文所提WGPR 算法可以在不同环境下得出较为精确的状态估计值。

为验证所提算法在三相负荷不平衡环境下的鲁棒性，设B 相负荷比例为100%且保持不变，以B相负荷比例为基准，以5%为步长，A 相依次减小至70%，C 相依次增大至130%。设置6 种不平衡情景下各相负荷不平衡比例如表6 所示。

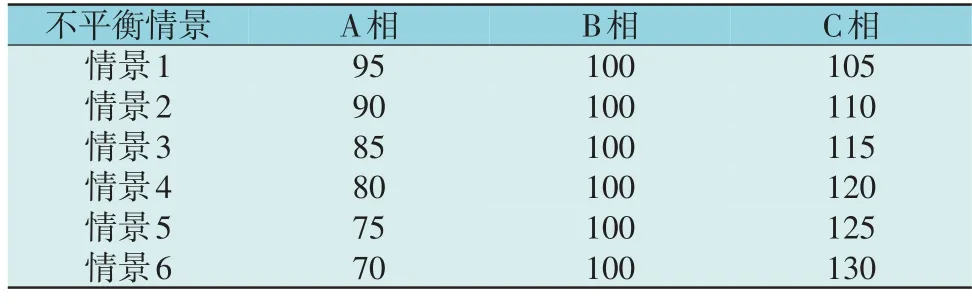
表6 6种不平衡情景下各相负荷不平衡比例Table 6 Unbalanced ratios of six unbalanced scenarios%

6 种不平衡情景下节点890 的B 相电压幅值估计值，如图8 所示。

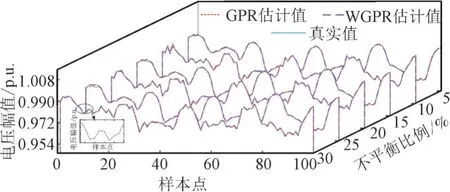
图8 6种不平衡情景下节点890的B相电压幅值估计值Fig.8 Estimated B-phase voltage amplitude of node 890 in six unbalanced scenarios

由图8 可知，与GPR 算法相比，WGPR 算法得出的估计曲线与真实曲线更加贴合，WGPR 算法在处理噪声时进行了加权操作，将GPR 算法的估计值和CNN-LSTM 算法的预测值进行加权回归，消除GPR 算法没处理的噪声，使得估计结果更加精确。

GPR 和WGPR 算法在6 种不平衡情景下节点890 的状态估计误差对比结果如表7 所示。

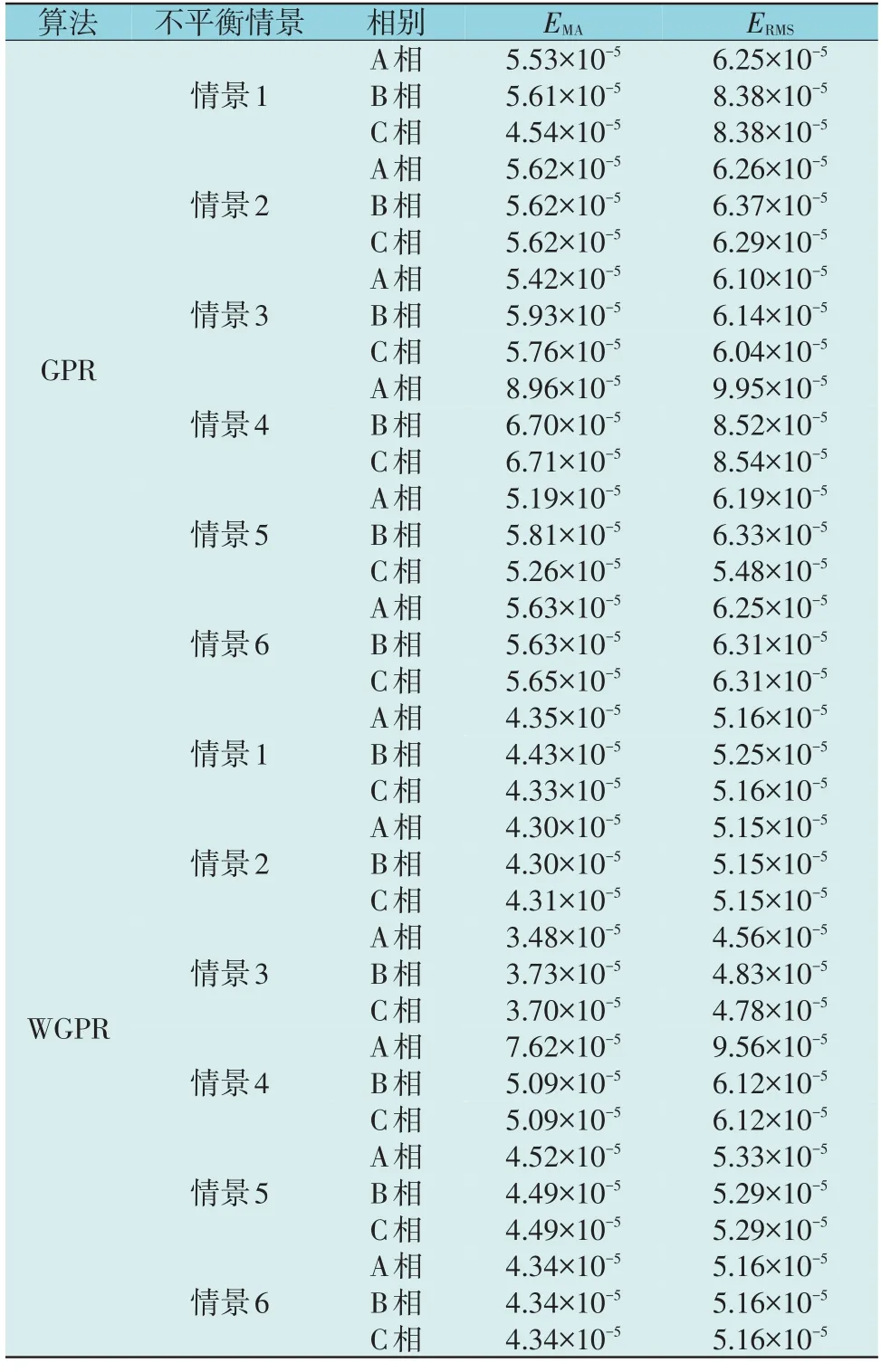
表7 6种不平衡情景下节点890的状态估计误差Table 7 State estimation errors of node 890 in six unbalanced scenarios

由表7 可知，2 种算法各相估计值与真实值的EMA和ERMS均保持在10-5数量级。与GPR 相比，本文所提方法的精度有23%左右的提升，并且估计结果不会随着不平衡比例的增大而增大，证明本文提出的配电网状态估计方法可在不同程度的不平衡比例下做出准确估计。

3.2 IEEE 123算例系统

为验证本文所提方法在大规模配电网中的有效性，在含DG 的IEEE 123 节点三相不平衡配电网进行测试如图9 所示。其中，在绿色节点接入光伏，在红色节点接入风电。因本文研究侧重点在三相不平衡方面，故在大算例中只考虑三相不平衡负荷的影响，对预测性能分析和系统抗噪能力测试不再阐述。

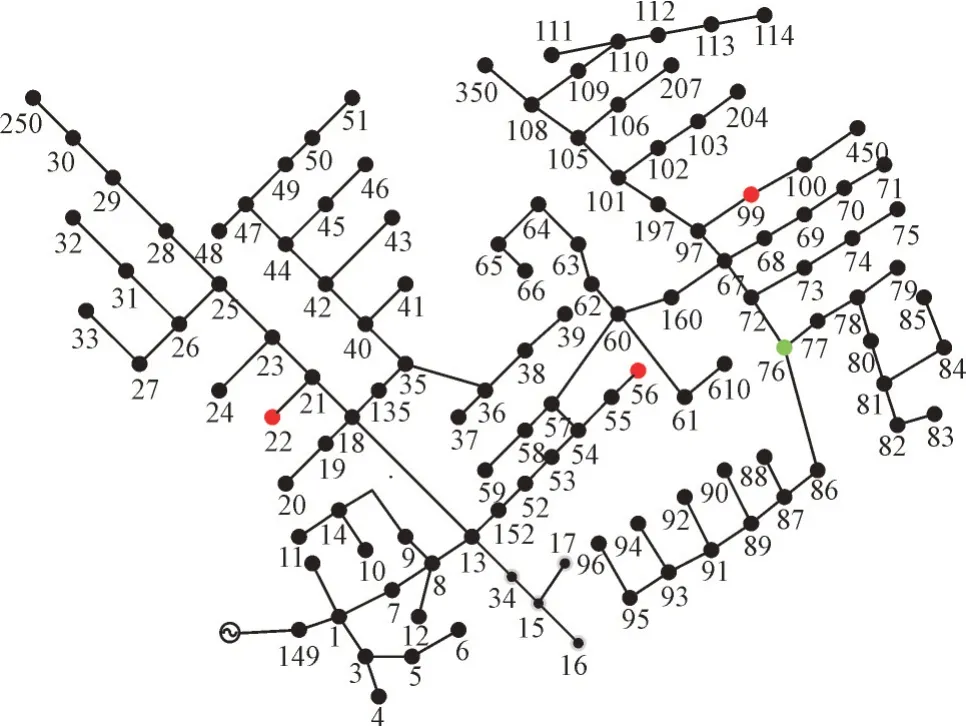
图9 含DG的IEEE 123节点三相不平衡配电网Fig.9 IEEE 123-bus three-phase unbalanced distribution system with DGs

IEEE 123 算例系统DG 属性如表8 所示。

表8 IEEE 123算例系统DG属性Table 8 Attribute table of DG in IEEE 123-bus example system

为测试大规模配电网WGPR 算法鲁棒性，以节点33 为例，得出不同场景下的EMA和ERMS。不同场景下节点33 状态估计性能如表9 所示。

表9 不同场景下节点33状态估计性能Table 9 State estimation performance of node 33 in different scenarios

由表9 可知，所提WGPR 算法得出的状态估计值与真实值依旧有良好的契合度，EMA和ERMS都维持在10-5数量级，具有良好的估计精度，计算所消耗的时间仍保持在ms 数量级。

对节点33 进行测试，6 种不平衡情景下节点33 的状态估计误差如表10 所示。

表10 6种不平衡情景下节点33的状态估计误差Table 10 State estimation errors of node 33 in six unbalanced scenarios

由表10 可知，与GPR 相比，WGPR 算法在不同场景下都有更高的精度，提高了14%左右，各相估计值与真实值的EMA和ERMS均保持在10-5数量级，所提方法的估计误差不会随着负荷不平衡比例的增大而增大，证明本文提出的状态估计方法可在不同程度的三相不平衡负荷下做出准确估计。

4 结论

在接入DG 的三相不平衡配电网以及存在非高斯量测噪声的背景下，为解决传统DNSE 方法鲁棒性差、状态估计精度不高的问题，提出一种基于WGPR 的鲁棒FASE 方法，并在IEEE 34 节点和IEEE 123 节点三相不平衡配电网中进行仿真，得出以下结论：

1）WGPR 算法与GPR 算法相比，可以在标准差较大的非高斯噪声环境中输出可靠的估计值，且在高噪声和量测数据异常的场景中依旧可以输出稳定的状态估计结果。

2）WGPR 算法可在DG 投入或者切出的情况下保持估计精度，具有良好的鲁棒性。

3）在不同的三相负荷不平衡程度下，WGPR 算法依旧保持稳定的估计结果，对三相不平衡配电网具有良好的适用性。