平抑百兆瓦级风电场功率波动的混合储能充放电协同控制策略
2023-12-05赵欣雨张云晓邱锦龙尚尔发张永昌赵海森
赵欣雨,张云晓,万 乐,邱锦龙,尚尔发,张永昌,赵海森
(1.新能源电力系统国家重点实验室(华北电力大学),北京 102206 2.内蒙古锡林郭勒盟电投新能源有限公司,内蒙古锡林浩特 026000)
0 引言
随着新能源发电技术和电力电子变换技术的迅猛发展,以及“碳达峰、碳中和”战略的快速推动,电力系统逐渐过渡到以高比例新能源和高比例电力电子装备为特征的新型电力系统阶段。新能源出力呈现间歇性、波动性和随机性的特点。因此大规模风电接入新型电力系统会给系统稳定、电网频率和电能质量等方面带来巨大挑战。如何有效平抑风电场出力波动,提高风电并网运行能力,对于促进风电大规模发展以及提升新型电力系统运行水平具有重要意义[1-3]。
多样化储能技术可在不同时间尺度上控制功率和能量的输入、输出,改善新型电力系统的稳定性和运行特性[4-6]。功率型和能量型储能存在技术互补特性,可有效抑制风电场在风力间歇性和随机性情况下产生的高频和低频功率波动,因此现有研究大多利用两者组成混合储能系统来平抑风电出力波动,如蓄电池-超级电容[7-8]、全钒液流电池-压缩空气储能[9]、飞轮-蓄电池[10]等混合储能系统。文献[11-12]分别采用傅里叶变换和统计方法对风功率曲线进行处理,从而确定储能出力及容量。文献[13-15]通过低通滤波、功率调节和限值管理对储能进行分层分级优化,最终实现风电波动平抑和储能合理工作。文献[16-17]提出具有可变滤波器时间常数的两阶段低通滤波器控制来优化混合储能的功率分配。文献[18]提出一种基于经验模态分解理论的风电功率平抑及混合储能功率分配方法。文献[19]在文献[18]基础上考虑风储系统净效益,提出基于滑动平均和经验模态分解的混合储能功率和容量配置方法,在实现风功率平抑的基础上得到经济性最优的配置方案。但经验模态分解存在边界效应和模态混叠问题。文献[20]利用两级实时小波滤波算法处理风电功率,两级滤波的作用分别为获得满足波动要求的功率以及去除噪声,同时采用荷电状态(State of Charge,SOC)反馈控制保持储能正常工作。小波包分解在小波分解的基础上提高了信号分析的时频分辨率,有助于获得信号高频部分的细节信息,更加适用于风电功率波动分析。文献[21]利用实时小波算法处理风电功率得到高频信号和低频信号并分别进行SOC 优化控制。文献[22-23]采用小波包分解(Wavelet Packet Decomposition,WPD)理论处理风电和光伏输出功率波动,风光原始出力被分解为并网低频信号和高频信号,根据混合储能技术特性进一步分解高频信号获得功率型和能量型储能出力。文献[24]建立包括分布式电源出力波动和微网供需平衡的评价指标,并提出基于WPD 和模糊控制的混合储能功率分配方法优化充放电功率,降低了分布式电源的波动性。当采用WPD 方法对风电原始出力进行分解时,为满足并网标准,所得风电并网功率曲线往往过于平滑,导致风电消纳率下降。且一些文献中的混合储能充放电控制策略往往针对SOC 进行优化,防止储能过度充放电,忽略了同一时序上能量型和功率型储能充放电状态不一致的问题,从而增加混合储能充放电转换次数,使各储能介质承担额外能量吸收与释放。
综上所述,为避免WPD 方法对风电波动功率的过度平抑,本文首先提出改进的WPD(IWPD)方法对原始风功率进行分解,得到较高的风电消纳功率及混合储能初始分配功率。在此基础上,为优化混合储能系统的充放电状态和充放电深度,提出基于时序-模糊优化的混合储能充放电协同控制策略对混合储能初始出力进行修正。仿真结果表明所提方法有利于提升新型电力系统中风电和混合储能系统协同运行能力。
1 基于IWPD的并网功率获取及混合储能初始功率分配
1.1 风储系统结构
图1 所示为典型风储系统结构,包括风电场、混合储能系统(包括电池储能和超级电容器储能)、电网和能量管理系统。其中,PCC 为公共连接点;SOC(tb),SOCs(tc)分别为电池和超级电容器在t时刻的荷电状态;P(tw),P(th),P(tb),Ps(tc),Pgri(td)分别为风电场、混合储能系统、电池、超级电容器输出功率和风电并网点功率。风电场、电池及超级电容器储能系统的输出功率汇集到公共母线,随后共同流向电网。能量管理系统通过收集各设备出力及SOC 等信息,合理控制储能出力,从而实现风电场功率波动平抑。
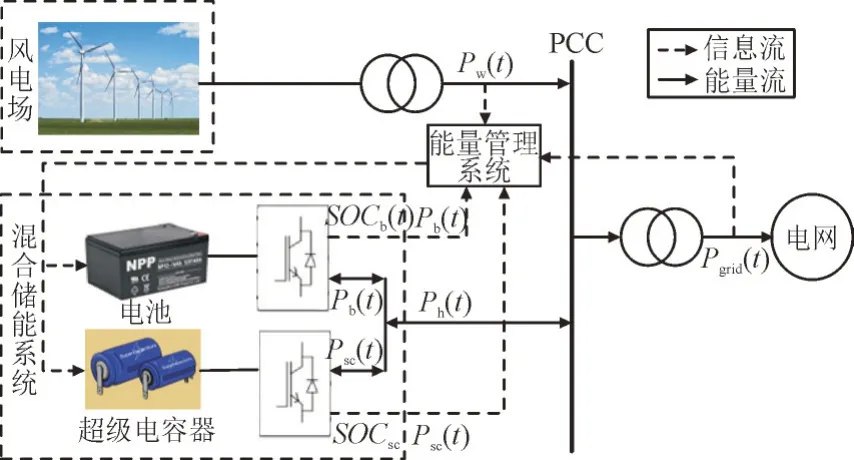
图1 风储系统结构Fig.1 Wind storage system structure
风储系统中能量流动关系如式(1)、式(2)所示。
P(tb)>0 或Ps(tc)>0 表示储能系统放电,反之表示储能系统充电。
1.2 基于IWPD的风储系统并网功率获取
为了充分发挥储能系统的经济效益并提高风力发电的利用率,只须保证风电功率波动满足GB/T 19963—2011 风电并网标准即可。WPD 具有良好的多分辨率和局部化特性,其在处理非平稳突变信号上更有优势,更加适用于风电功率波动平抑,其示意图如图2 所示。由图2 可知,S为初始信号,通过对S进行m(m≥1)层分解(m为分解层数),得到2m个频段的信号,分解后的信号从低频到高频分别定义为Sm,0,Sm,1,...,Sm,2m-1。第m层每个信号频段的带宽为Δf=fs/2m+1。
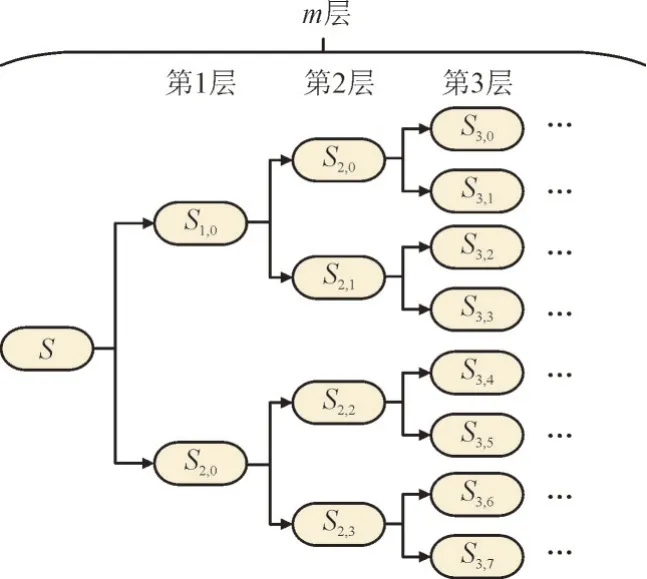
图2 WPD示意图Fig.2 Schematic diagram of WPD
由于本文研究的信号是风电场实时波动功率数据,在风速条件恶劣的情况下,风电功率变化较大且无规律,因此应选择信号突变分解能力和时频局部分析能力突出的小波基。dbN小波具有较强的频域局部分析能力和理想的幅频特性,在工程实际中应用广泛。其特点是随着阶次(序列N)的增大消失矩阶数越大,其中消失矩越高光滑性越好,频域的局部化能力就越强,频带的划分效果越好,但会使时域紧支撑性减弱,同时计算量大大增加,实时性变差。因此综合考虑风电功率曲线的平抑效果及计算时间,选择较为高阶的db5 小波对风电原始输出功率进行小波包分解。
当采用WPD 对风电功率进行分解时,往往将得到的低频分量Sm,0作为风电并网功率。但在通过加大分解层数来获得满足并网标准的风电曲线时,往往会使得原始波动率较小区间内的功率曲线过于平滑,在一定程度上降低了风电消纳量。因此,本文提出IWPD 方法处理风电原始出力信号,步骤如下:
1)令m=1,对风电原始出力进行m层小波包分解。
2)计算低频信号Sm,0是否满足GB/T 19963—2011 标准。
3)若不满足,令m=m+1,继续对风电原始输出功率进行WPD,并重复步骤2);若满足并网标准,输出此时的m。
4)取Sm,(t0)与Sm-1,(t0)之中的最大值,记为Sma(tx)=max[Sm,(t0),Sm-1,(t0)];并找到Sm,(t0)与Sm-1,(t0)相等时对应的时刻,从小到大依次记为t1,t2,....,tn。
5)计算Sma(tx)曲线是否满足并网标准。
6)若Sma(tx)曲线满足并网标准,则风电并网功率为Pgri(td)=Sma(tx)。
7)若Sma(tx)曲线不满足并网标准,定义修正区间如下式(3)所示:
式中:Tcs和Tcl分别为1 min 和10 min 时间尺度波动越限修正区间,在满足约束条件前提下应使得Tcs和Tcl的区间长度尽可能小;Ti为初始区间,Ti=[ti,ti+1],ti为Sm,(t0)和Sm-1,(t0)相等时对应的第i个时刻;Fsi和Fli分别为1 min 和10 min 时间尺度下Ti区间中实际波动最大值;Fsmax和Flmax分别为1 min 和10 min时间尺度下规定的波动限值。
按照式(4)修正风电并网功率:
式中:Sma(tx)为Sm,(t0)和Sm-1,(t0)之中的最大值;t为采样时间;a1,a2为修正参数,a1,a2∈[0,1],在Pgri(td)满足并网标准前提下,a1,a2取最小值。
按照步骤4)—步骤7)对WPD 进行改进,可在风电波动满足并网标准前提下获得更多的风电消纳量。
1.3 基于IWPD的混合储能初始功率分配
根据电池和超级电容器的充放电响应特性[25],选择1min 作为两者充放电响应时间的分界,响应频率为1.67×10-2Hz。因此电池和超级电容器各自需要承担的波动功率如式(5)所示。
式中:Pbref,Pscref分别为电池和超级电容器的初始分配功率;k为电池和超级电容器功率信号的分频点,通过频谱分析获得,取整数;Sm,k,Sm,k+1,Sm,k+2分别为经过m层小波包分解后第k,k+1,k+2 个频段的信号。
2 基于时序-模糊优化的混合储能充放电协同控制策略
本文在混合储能初始功率分配基础上,针对能量型和功率型充放电状态不一致问题,提出基于一致性指标的混合储能充放电时序优化方法对混合储能初始分配功率进行一次修正;然后针对混合储能SOC 越限问题,采用模糊优化方法对混合储能功率进行二次修正。所提混合储能充放电协同控制策略如图3 所示。其中,C为混合储能系统充放电一致性指标;ΔSOCs(tc+1),ΔSOC(tb+1)分别为t+1时刻超级电容器和电池的荷电状态变化量;Psc(t1),Pb(t1)分别为一次修正后超级电容器和电池的出力;Psc(t2),Pb(t2)分别为二次修正后超级电容和电池的出力;ΔPsc2为超级电容器功率指令第二次修正前后的差值。
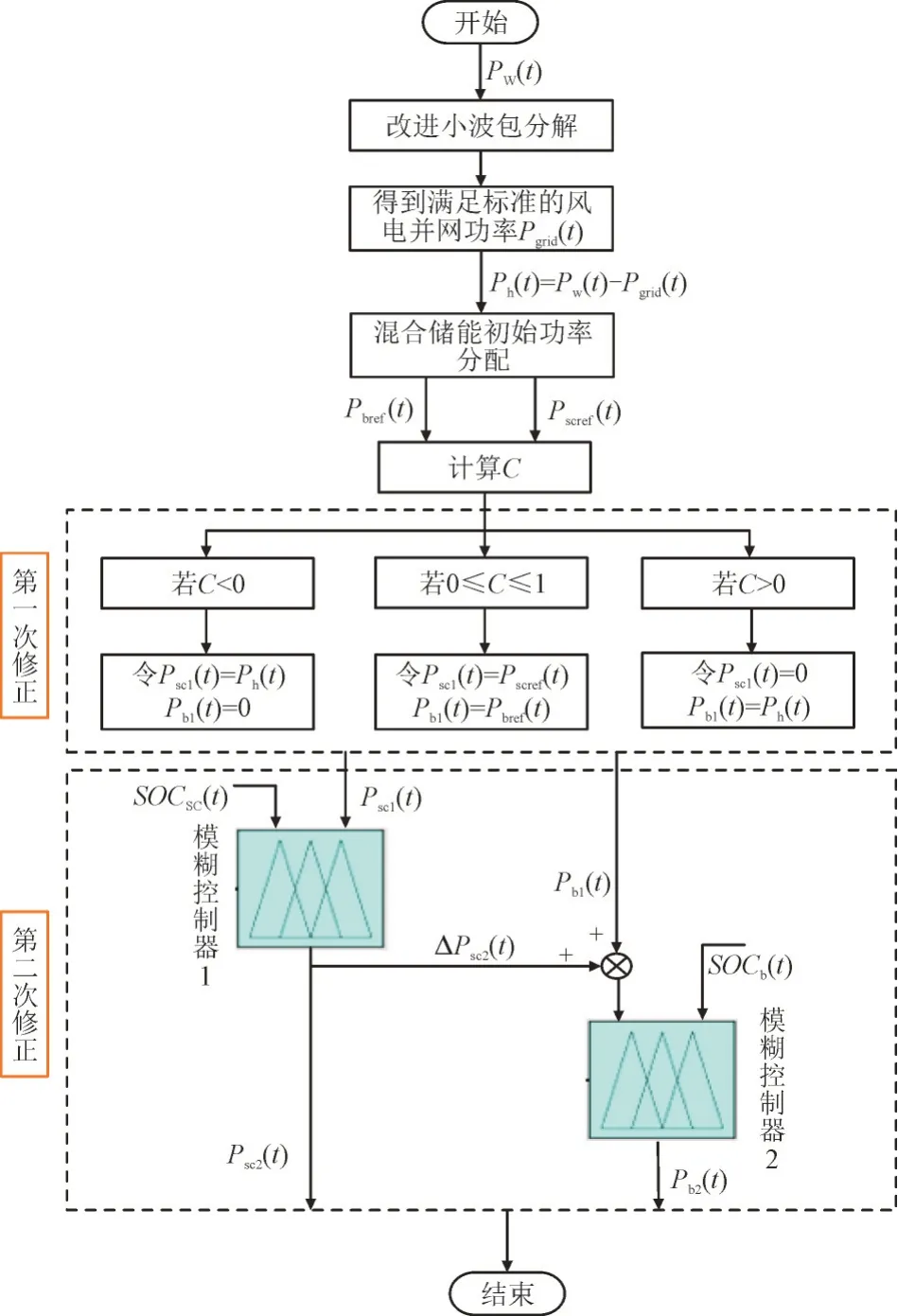
图3 混合储能系统充放电协同控制策略Fig.3 Charge-discharge cooperative control strategy for hybrid energy storage system
2.1 基于一致性指标的混合储能充放电时序优化
为了判断混合储能系统充放电状态,定义混合储能系统充放电一致性指标C,如式(6)所示。
若0≤C≤1,表明混合储能系统均处于充电或放电状态或一种储能处于充电或放电状态,另一种储能不工作;若C<0 或C>1,表明混合储能系统处于“一充一放”状态。
针对混合储能充放电状态不一致问题,提出充放电时序优化方法对混合储能初始分配功率进行一次修正,其优化过程如下:
1)当0≤C≤1 时,Psc(t1)=Pscre(tf),Pb(t1)=Pbr(tef)。
2)若C<0,则|Pscre(tf)|>|P(th)|,说明混合储能系统处于“一充一放”状态,导致同一时序上的充放电状态不一致,此时令Psc(t1)=P(th),Pb(t1)=0。
3)若C>1,则|Pscr(tef)|<|P(th)|,此时令Pb(t1)=P(th),Psc(t1)=0。
经过第一次修正后,各储能介质能在同一时序上同步地平抑风电波动功率。
2.2 基于SOC越限的混合储能系统模糊优化
如图3 所示,在第一次修正基础上,采用模糊优化对储能SOC 越限问题进行第二次修正。模糊控制器1 的输入变量为超级电容器的SOCs(tc)和ΔSOCs(tc+1),模糊控制器2 的输入变量为电池的SOC(tb)和ΔSOC(tb+1)。其控制策略如下:
1)第一次修正后计算SOCs(tc),若SOCs(tc)适中,保持第一次修正后的超级电容器充放电策略不变;若SOCs(tc)偏大且下一时刻Psc(t1+1)<0 或SOCsc(t)偏小且下一时刻Psc(t1+1)>0,对超级电容器出力进行第二次修正,输出修正系数Ks(tc),二次修正后超级电容器功率指令为Psc(t2)=Ks(tc)·Psc(t1)。模糊控制器1 的模糊控制规则如下:当△SOCs(tc+1)>0时,SOCs(tc)越大,输出变量Ks(tc)应越小;同理,当△SOCs(tc+1)<0 时,SOCs(tc)越小,输出变量Ks(tc)应越小。Ks(tc)∈[0,1]。模糊控制器1 的隶属函数和模糊规则如图4 和表1 所示。
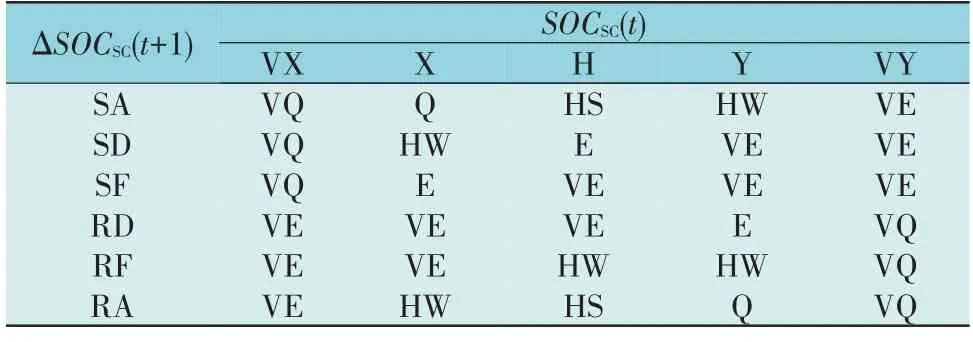
表1 模糊控制器1的控制规则Table 1 Control rules for fuzzy controller 1
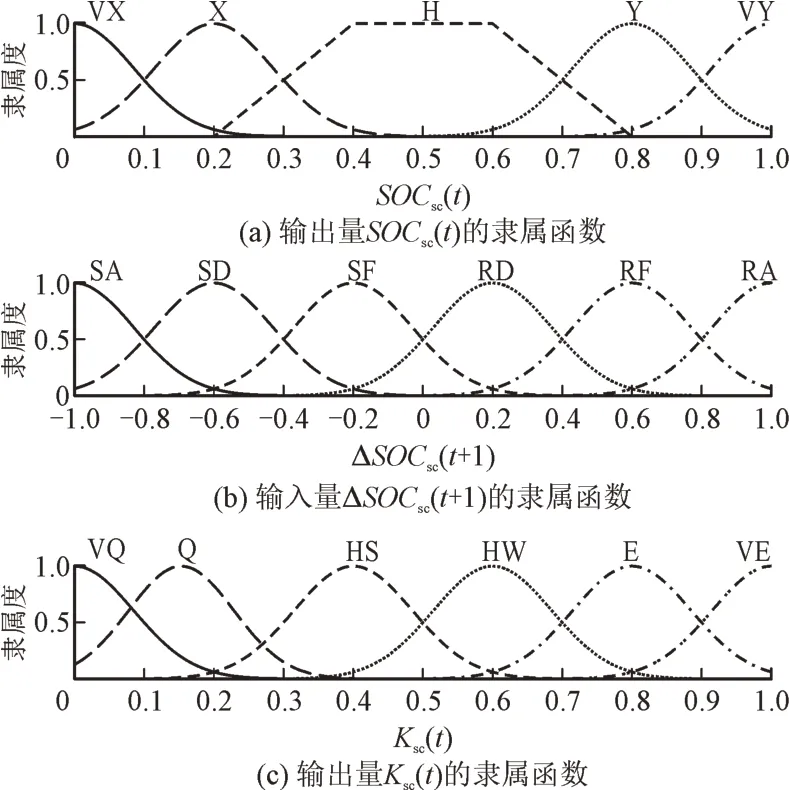
图4 模糊控制器1的隶属函数Fig.4 Membership functions for fuzzy controller 1
图4 中,VX,X,H,Y,VY 为输入量SOCs(tc)的模糊子集;SA,SD,SF,RD,RF,RA 为输入量ΔSOCs(tc+1)的模糊子集;VQ,Q,HS,HW,E,VE 为输出量Ks(tc)的模糊子集;SOCs(tc),ΔSOCs(tc+1),Ks(tc)为标幺值,无量纲。
2)超级电容器功率指令第二次修正前后的差值ΔPsc2由电池补偿。其中ΔPsc(t2)=Psc(t1)-Psc(t2),模糊控制器2 按照步骤1)相同的策略对蓄电池的SOC(tb)进行优化。输出修正系数K(tb),模糊控制器2 的隶属函数及模糊规则如图5 和表2 所示。其中,VT,T,PT,L,PF,F,VF 为输入量SOC(tb)的模糊子集;QA,QD,QF,ZD,ZF,ZA 为输入量ΔSOC(tb+1)的模糊子集;VI,I,PI,U,PL,D,VL 为输出量K(tb)的模糊子集。二次修正后的蓄电池的功率指令为Pb(t2)=K(tb)·(Pb(t1)+ΔPsc(t2))。

表2 模糊控制器2的控制规则Table 2 Control rules for fuzzy controller 1
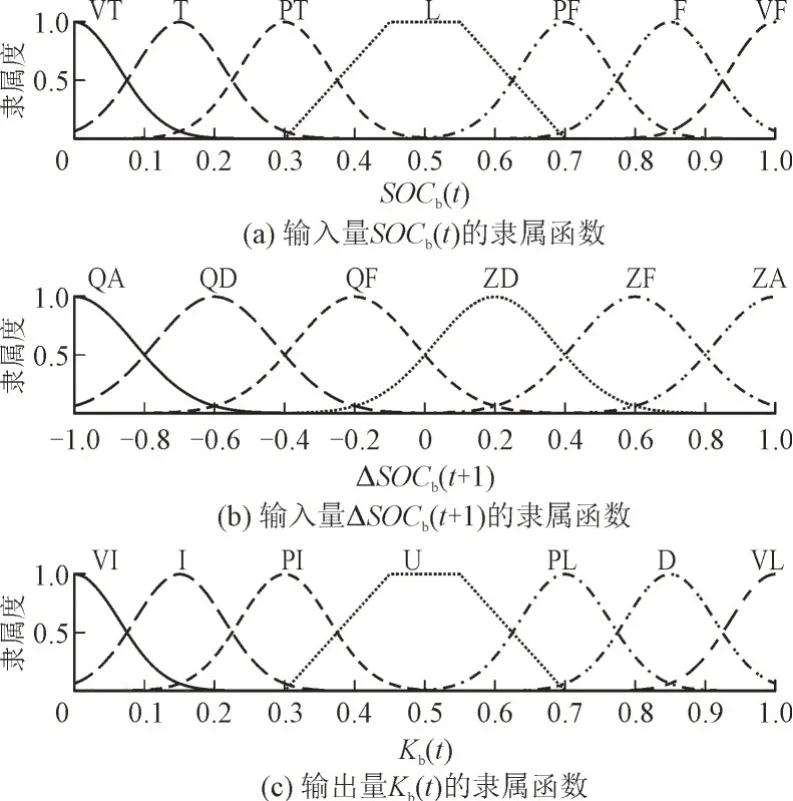
图5 模糊控制器2的隶属函数Fig.5 Membership functions for fuzzy controller 2
3 算例分析
为验证本文所提策略的有效性,以某内蒙古100 MW 风电场的典型日输出功率为例,利用电池-超级电容器混合储能系统平抑风电输出功率波动,风储系统结构如图1 所示。采用本文所提控制方法得到风电并网功率和混合储能系统输出功率信号。
3.1 风电功率波动平抑效果及风电消纳量分析
图6 为风电原始输出功率和分别采用WPD 和IWPD 方法得到的并网功率。图6 中180—240 min时段和550—850 min 时段的放大图表示不同时间尺度下原始风功率及并网功率曲线的最大波动值及其所在时段。表3 为2 种方法得到的风电平抑效果及风电消纳量结果。根据GB/T 19963—2011标准,100 MW 风电场在1 min 和10 min 时间尺度下的波动限值分别为10 MW 和33.3 MW[22]。

表3 IWPD与WPD算法结果对比Table 3 Comparison of IWPD and WPD algorithm results
由图6 和表3 可知,采用WPD 方法对风电原始出力进行5 层分解后,风电1 min 时间尺度下波动功率最大值由原始的12.04 MW 减小为4.83 MW,这会使得风电并网曲线过度平滑,导致风电消纳量降低。而采用本文所提IWPD 方法后,计算得到风电功率修正参数a1=0,a2=0.4,此时风电1 min 时间尺度下波动功率最大值由原始的12.04 MW 减小为7.65 MW。在同样满足风电并网标准前提下,IWPD 方法比WPD 方法得到的典型日风电消纳量多123 kWh,说明文中IWPD 方法能够在保证风功率满足并网标准的前提下,提高风电消纳量。
3.2 混合储能充放电时序优化效果分析
在采用IWPD 方法得到风电并网功率后,通过频谱分析得到混合储能功率分频点k=4,并按照图3所示混合储能优化控制策略对储能出力进行优化。图7 为混合储能系统初始输出功率及第一次、第二次修正后的输出功率。

图7 混合储能初始输出功率及两次修正后输出功率Fig.7 Initial output power and output power after two corrections of HESS
由图7 可知,以440—600 min 时段为例,在仅对混合储能进行初始功率分配时,混合储能系统存在“一充一放”现象,导致混合储能系统产生额外的能量吸放,使得总体运行效率降低;而在进行第一次修正后(充放电时序优化后),电池和超级电容器能在同一时序上同步地进行充电或放电。与不考虑充放电时序优化相比,第一次修正后电池充放电转换次数从71 次减少到14 次,超级电容器充放电转换次数从390 次减少到61 次,混合储能系统减少了不必要的充放电能量13.54 MWh。因此第一次修正后混合储能系统充放电转化次数及充放电能量大大减少,有利于提高混合储能系统的运行效率及使用寿命。
3.3 混合储能SOC优化效果分析
第二次修正在第一次修正的基础上优化混合储能系统的SOC,规定混合储能SOC 在0.2~0.8 之间。根据文献[24]计算电池储能和超级电容器储能的容量分别为5.98 MWh 和1.69 MWh。为说明本文所提方法的有效性,分别采用2 种优化方法对SOC 进行优化:(1)文献[24]中模糊优化方法;(2)本文所提考虑充放电时序的模糊优化方法。不同优化控制策略下电池和超级电容SOC 变化情况如图8 和图9 所示。
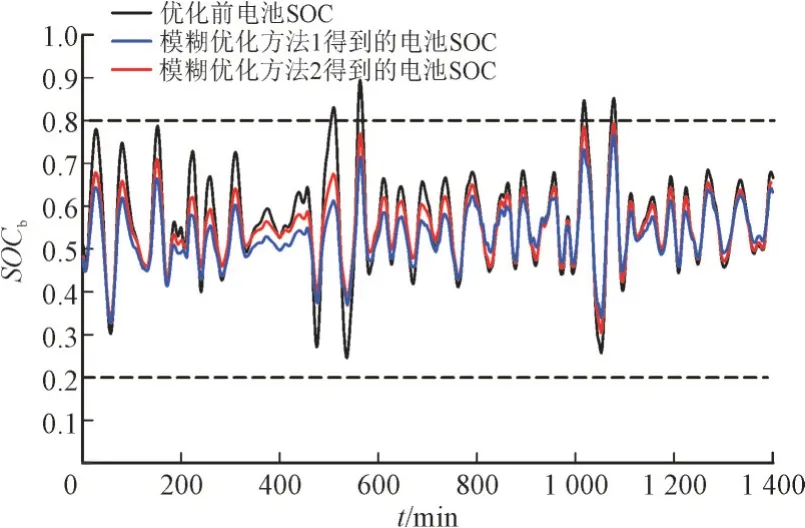
图8 不同优化方法下电池储能SOCFig.8 SOC of battery energy storage under different optimization methods

图9 不同优化方法下超级电容器储能SOCFig.9 SOC of supercapacitor energy storage under different optimization methods
由图8 和图9 可知,2 种优化控制方法都可将电池和超级电容器的SOC 控制在0.2~0.8 范围内,其对电池储能SOC 的优化效果相差不大,而在2 种优化控制方法下的超级电容器SOC 随时间的变化情况存在较大差异。第一种优化方法虽然能控制超级电容器SOC 在0.2~0.8 之间,但SOC 变化幅度较大且接近30%的时间处于充放电裕度较高的区域;相比于第一种优化方法,本文所提考虑充放电时序的模糊优化方法得到的超级电容器SOC 的工作区间得到很大改善,SOC 曲线较为平缓且约90%的时间SOC 保持在[0.4,0.6]之间。因此本文所提考虑充放电时序的模糊控制方法能够有效降低储能系统的充放电深度,防止其过度充放电,有利于实现混合储能系统的充放电协同运行。
4 结语
本文应用电池-超级电容器混合储能系统对百兆瓦级风电场出力波动进行平抑,分别提出IWPD和混合储能充放电协同控制策略对风电并网功率和混合储能系统出力进行优化。所提IWPD 可在保证风电平抑效果基础上提升风电消纳能力;所提基于时序-模糊优化的混合储能充放电协同控制策略可使各储能在同一时序上同步地充电或放电,减少了充放电转换次数及累积充放电能量,降低了储能系统的充放电深度,实现了能量型和功率型储能技术的协同运行。
