研究降雨事件对交通流时空特性的影响

陈华伟，邵毅明*,b，敖谷昌,b，张惠玲,b

(重庆交通大学a.交通运输学院；b.山地城市交通系统与安全重庆市重点实验室，重庆400074)

0 引 言

时空相关性分析认为道路是一种时空对象，其交通流状态在时间上延续，在空间上与近邻道路状态相互作用[1]，因此，道路交通流具有状态值和影响值的双重时空特性.道路交通流时空特性受多种因素影响，在自然环境因素中，降雨事件对其有显著影响.有关降雨事件对交通流时空特性的影响研究侧重于对状态值的影响研究，鲜有对影响值的影响研究.降雨事件对状态值的影响研究主要可以总结成两类：

(1)基于显性关系的分析.李长城[2]构建了道路速度与降雨量的回归模型，和飞飞[3]构建了道路速度变化量与降雨量的回归模型.基于显性关系的分析，构建交通流状态值或状态值变化量与降雨量的连续函数，描述降雨量对交通流状态值的影响.

(2)基于隐性关系的分析.Essien[4]研究了降雨对道路速度、流量和密度三者关系的影响，Xu[5]研究了降雨对路网积累车辆数和路网输出车辆数两者关系的影响.基于隐性关系的分析将降雨事件划分成多个等级，研究各等级降雨事件下交通宏观模型的变化.

本文借鉴上述分析方法，划分降雨事件等级，研究各等级降雨事件下交通流时空特性的分布类型，当分布类型一致时，通过对比分布统计量，可以量化降雨事件对交通流时空特性的影响，分析道路类型的转变方向和程度.

1 数据描述

1.1 数据采集

数据采集的主要内容包括状态值数据和降雨量数据，状态值数据为重庆市局部路网的状态值数据，降雨量数据为重庆市主城某区的降雨量数据，路网布局如图1所示.

(1)状态值数据.

描述交通流运行状态的参数众多，常以速度作为研究对象.状态值数据以30 min为间隔，由路网的微波检测器(RTMS)和射频识别技术(RFID)采集，汇总结果如表1所示.

(2)降雨量数据.

降雨量数据由和风天气的天气数据开发平台提供，该平台提供了降雨量查询API.API本质上是调用函数，由平台服务器名、请求参数及其数值组成.用户根据需求为请求参数赋值，经计算机发出请求，平台服务器按照请求返回响应，最后通过编程语言解析响应并存储数据.降雨量数据采集以30 min为间隔，汇总结果如表2所示.

图1 路网布局Fig.1 Road network layout

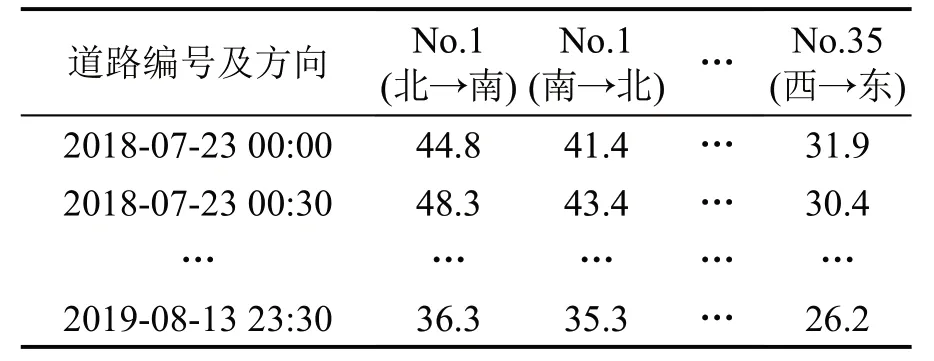
表1 原始状态值数据Table1 Original state value data (km/h)

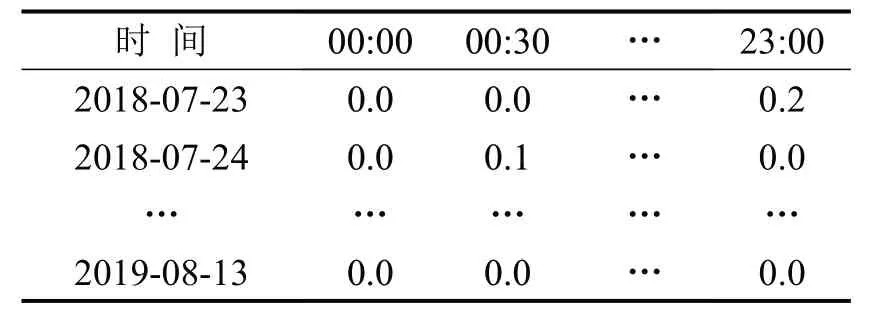
表2 降雨量数据Table2 Precipitation data (mm/30 min)

1.2 数据处理

状态值数据服从正偏性的正态分布[6]，通过对状态值数据进行自然对数转换[7]，可以减弱状态值数据分布的正偏程度.自然对数转换过程为

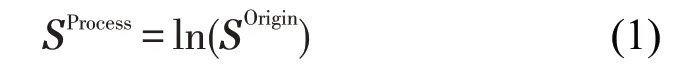
式中：SOrigin为原始数据；SProcess为自然对数转换后的数据.

自然对数转换后的状态值数据如表3所示.

表3 自然对数转换后的状态值数据Table3 State value data after natural logarithm transformation

2 交通流时空特性

路网有e条道路(双向)，路网道路集合为E={1,…,e}，对路网进行m天观测，观测日集合为D={1,…,m}，观测日包含n个观测时刻，观测时刻集合为T={1,…,n}.

(1)交通流状态值.

交通流状态值是描述交通流运行状态的参数的统称，常以速度作为研究对象，记为表示观测日d时刻t的路网交通流状态值向量，由各道路交通流状态值组成，其中，道路k∈E，观测日d∈D，观测时刻t∈T.

(2)交通流影响值.

交通流影响值是道路交通流状态值波动对其相交道路状态值的影响，记为表示观测日d时刻t的路网交通流影响值向量，由各道路交通流影响值组成，其中，k∈E，d∈D，t∈T.路网道路通过将状态值波动传播至相交道路，实现路网的状态值波动守恒，可将道路的状态值波动视为其相交道路状态值波动的线性组合，即

式中：SNET为状态值波动向量，为当前时刻与上一时刻状态值的差值W为状态值波动传播结构向量由各道路状态值波动传播结构组成；SNEI为相交道路的状态值波动矩阵其元素取值为

式中：为道路k的影响值；Ek为道路k相交道路集合；为道路x的传播结构.

(3)交通流时空特性.

Moran散点图能直观反映时空对象的时空特性[8]，将Moran散点图移植到交通流中，绘制交通流时空特性的Moran散点图，如图2所示，其中计算过程为

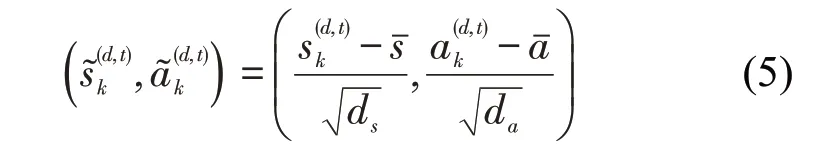
图2 交通流时空特性Moran散点图Fig.2 Moran scatterplot of spatio-temporal characteristics of traffic flow

道路1失效水平低()，影响水平高(0)，记作潜在关键道路；道路2失效水平低(0)，影响水平低(≤0)，记作非关键道路；道路3失效水平高(≤0)，影响水平低(≤0)，记作非传播型拥堵道路；道路4失效水平高影响水平高记作关键道路.

3 降雨事件对交通流时空特性的影响

3.1 基本思路

交通流时空特性受多种因素影响，仅构建交通流时空特性与降雨量的回归模型，无法兼顾其他因素的影响，模型误差大.在长时间的统计周期内，各等级降雨事件下交通流时空特性具有稳定的统计分布，因此，当各等级降雨事件下交通流时空特性的分布类型一致时，通过对比分布统计量，量化降雨事件对交通流时空特性的影响.

3.2 影响因素

(1)降雨事件等级.

降雨事件按照降雨量大小可划分成无雨、零星小雨、小雨、中雨、大雨、暴雨等8个等级[9].将零星小雨和小雨2个等级合并为小雨；将暴雨及以上共3个等级合并为暴雨；将降雨事件汇总成5个等级，各等级降雨事件划分标准如表4所示.

表4 降雨事件划分标准Table4 Classification standard of rainfall events(mm)

定义降雨事件的标识符集合为Slevel={nr,lr,mr,hr,rs}，其中，nr、lr、mr、hr、rs分别为无雨、小雨、中雨、大雨、暴雨的标识符.

(2)时 段.

综合图3和图4可以看出，在250个工作日内，02:00-03:30 (平峰)和07:30-09:00 (高峰)的交通流时空特性差异大，则以这2个时段进行对比分析.

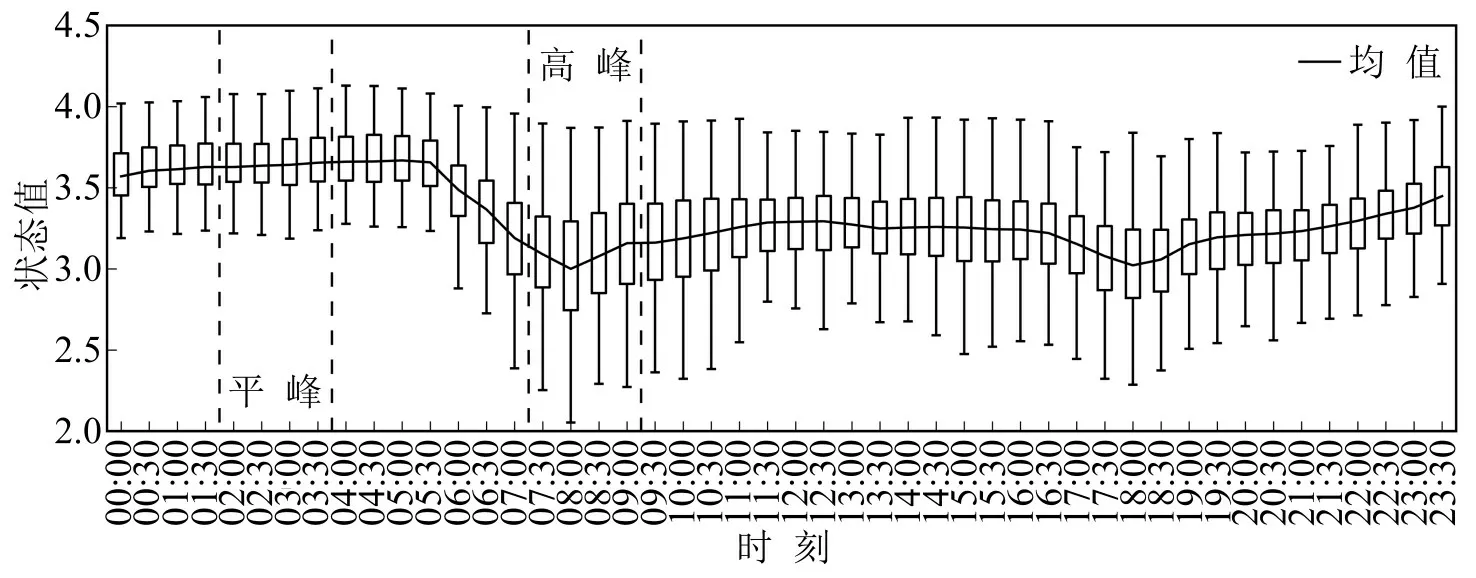
图3 路网道路状态值箱型图Fig.3 Box diagram of state value in road network

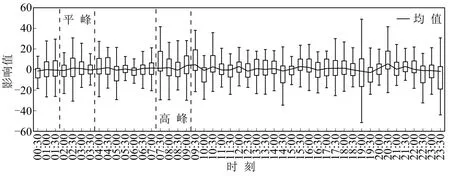
图4 路网道路影响值箱型图Fig.4 Box diagram of affect value in road network

时段的标识符集合为Speriod={o,p}，其中，o、p分别为平峰和高峰时段的标识符.

3.3 降雨事件对状态值的影响

建立由2个时段和5个降雨事件交叉形成的10个状态值子集，根据交通流状态值所处的时段和降雨事件不同，将其划分到对应的子集中，即

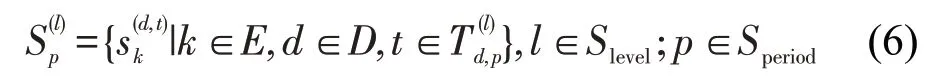
根据划分的子集，绘制状态值的概率密度直方图，并对概率密度进行正态拟合，绘制拟合曲线，如图5和图6所示.

状态值概率密度的拟合结果及评价如表5所示.

图5 状态值概率密度直方图及其拟合曲线图(平峰)Fig.5 Probability density histograms and their fitting curve chart of state value(off-peak period)

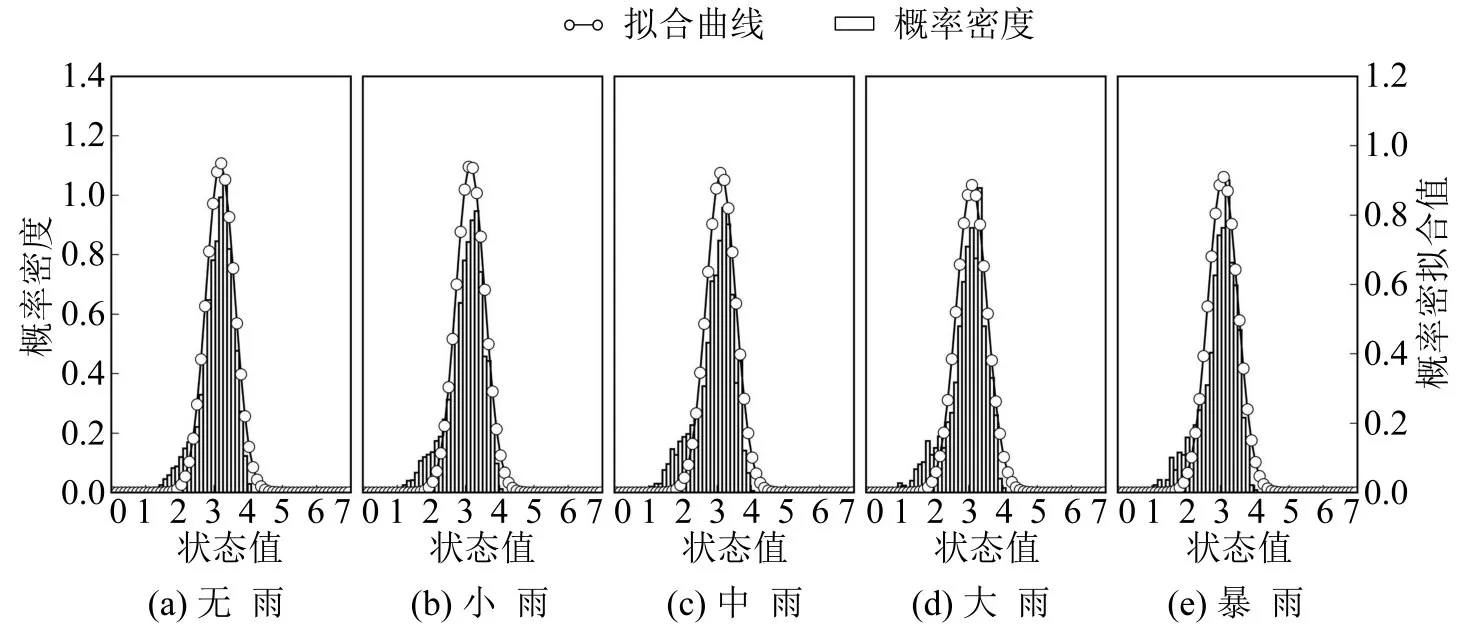
图6 状态值概率密度直方图及其拟合曲线图(高峰)Fig.6 Probability density histograms and their fitting curve chart of state value(peak period)

表5 状态值概率密度拟合结果及评价Table5 Fitting result and evaluation of state value probability density

从表5可以看出，平峰时段内，均方根误差(Root Mean Square Error,RMSE)介于0.12～0.14，R2基本大于0.65，拟合效果可以接受；高峰时段内，RMSE介于0.05～0.07，R2均大于0.90，拟合效果很好.因此，在平峰和高峰时段内，各降雨事件下状态值均服从正态分布.

在正态分布统计量中，期望反映了状态值波动的中心值，可作为对比统计量，记为.根据状态值期望，计算相较无雨事件状态值的期望，各降雨事件下状态值期望的降低率，计算公式为

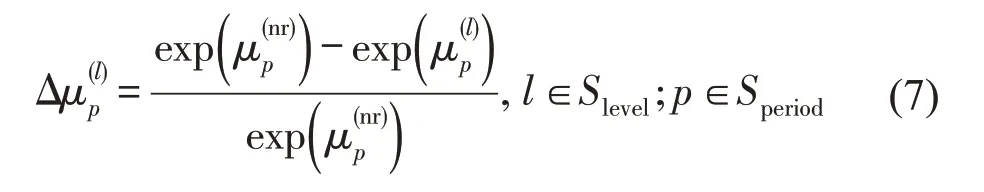
平峰时段内，各降雨事件下状态值期望的降低率依次为0、1.00%、1.98%、2.96%、3.92%；高峰时段内，各降雨事件下状态值期望的降低率依次为0、4.88%、7.69%、9.52%、10.42%.

从横向对比看，在同一时段内，随着降雨事件等级的提升，状态值期望逐渐降低，状态值期望的降低率逐渐升高；从纵向对比看，在同一降雨事件下，高峰时段的状态值期望低于平峰时段，高峰时段的状态值期望降低率高于平峰时段.图7可证实上述规律.

图7 路网全时段状态值期望Fig.7 Expectation of state value in road network in full time period

3.4 降雨事件对影响值的影响

建立由2个时段和5个降雨事件交叉形成的10个影响值子集，根据交通流影响值所处的时段和降雨事件不同，将其划分到对应的子集中，即

式中：为在p时段内，降雨事件为l时的影响值子集.

根据划分的子集，绘制影响值的概率密度直方图，并对概率密度进行正态拟合，绘制拟合曲线，如图8和图9所示.

图8 影响值概率密度直方图及其拟合曲线图(平峰)Fig.8 Probability density histograms and their fitting curve chart of affect value(off-peak period)

图9 影响值概率密度直方图及其拟合曲线图(高峰)Fig.9 Probability density histograms and their fitting curve chart of affect value(peak period)

影响值概率密度的拟合结果及评价如表6所示.

表6 影响值概率密度拟合结果及评价Table6 Fitting result and evaluation of affect value probability density

从表6可以看出，平峰时段内，RMSE介于0.02～0.04，R2均大于0.95，拟合效果很好；高峰时段内，RMSE介于0.02～0.06，R2均大于或等于0.90，拟合效果很好.因此，在平峰和高峰时段内，各降雨事件下影响值均服从正态分布.

从横向对比看，在同一时段内，随着降雨事件等级的提升，影响值期望无显著变化规律；从纵向对比看，在同一降雨事件下，高峰时段与平峰时段的影响值期望无显著变化规律.这是由于降雨事件对各道路交通流状态值的影响具有相似性，道路间状态值波动的比例基本不变，则影响值也基本不变，因此，降雨事件对影响值期望无显著影响，图10可验证上述分析.

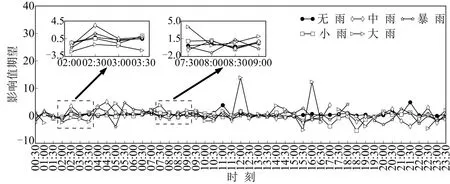
图10 路网全时段影响值期望Fig.10 Expectation of affect value in road network in full time period

3.5 降雨事件下道路类型演变

按照道路k不同，将和分别划分成和对和进行正态拟合.以无雨事件下状态值和影响值的拟合期望和方差为基础，对有雨事件下状态值和影响值的拟合期望进行z-score 标准化.为反映交通流时空特性点的聚集程度，将Moran 坐标系划分成多个0.1×0.1 方块，统计方块内的点，并用颜色描述方块内点的个数，以热力图形式绘制Moran散点图，如图11和图12所示.

图11 各降雨事件下Moran散点图(平峰)Fig.11 Moran scatterplots in every rainfall event(off-peak period)

图12 各降雨事件下Moran散点图(高峰)Fig.12 Moran scatterplots in every rainfall event(peak period)

从图11和图12 总体上看，相较无雨事件，有雨事件发生时，道路类型总体由低失效道路向高失效道路转变；从横向对比看，在同一时段内，随着降雨事件等级的提升，虽然状态值期望总体逐渐降低，但低失效道路与高失效道路的比例基本不变；从纵向对比看，在同一降雨事件下，高峰时段的状态值期望总体低于平峰时段，高峰时段的高失效道路多于平峰时段.可以看出，低影响道路与高影响道路之间的转变并不显著.

4 结 论

对比各降雨事件下交通流时空特性的期望，可量化降雨事件对交通流时空特性的影响，分析道路类型的转变方向和程度，主要规律有：随着降雨事件等级的提升，状态值期望逐渐降低，状态值期望的降低率逐渐升高；降雨事件对影响值期望无显著影响；相较无雨事件，有雨事件发生时，道路类型总体由低失效道路向高失效道路转变；随着降雨事件等级的提升，低失效道路与高失效道路的比例基本不变；在同一降雨事件下，高峰时段的高失效道路多于平峰时段的.