基于统计推断的异常光伏组件识别方法
2023-12-05袁廷璧彭咏龙王文彬段震清柳殿彬崔亚辉
陆 江,袁廷璧,彭咏龙,王文彬,段震清,柳殿彬,崔亚辉
(1.华北电力大学电气与电子工程学院,河北保定 071000;2.国家能源集团新能源技术研究院,北京 102200)
0 引言
在“双碳”政策的推动下,国内大规模兴建光伏电站,但目前光伏行业忽略运维而重视基建,导致电站低能效问题日趋加重,光伏组件发电效率的高低直接影响电站的发电量,对阵列中能效异常的组串、组件进行识别,提示运维人员进行维护,可有效提高电站发电量[1-4]。
国内外学者做了大量有关光伏组件异常识别的研究。湖南大学的钱吉红[5]通过对各环节的损耗模型进行能效分析,提出了一种能效测试和评价方法,通过与中位数、历史平均值进行对比,识别异常设备。武文栋等人[6]提出了一种基于改进麻雀搜索算法优化RBF 神经网络(Improved Sparrow Search Algorithm Optimized Radial Basis Function Neural Network,ISSA-RBF)的光伏故障诊断方法。王方政等人[7]通过将传统的电压、电流定位法、时间跟踪描述和光伏电池参数估计模型相结合,给出一种故障诊断方法,判断热斑故障发生的位置和严重程度。LI Weijun 等人[8]提出了一种基于层次分析法和模糊综合评判的光伏发电系统能效评价方法,该方法分析了影响光伏发电系统能效的因素,建立了光伏发电系统的能效评价指标体系。太原理工大学的李莎等人[9]提出一种软阈值化的时序卷积神经网络的组件异常识别模型。马纪梅等人[10]以异常特征为判据,给出一种基于K 均值聚类算法的改进RBF 神经网络的光伏组件异常识别方法。
目前识别组件异常状态的技术主要基于对组件I-V特性曲线的分析来实现[6,7,9-14],而实际工程中组件数量众多,I-V曲线获取困难,若只讨论阵列的异常程度,将会忽略其中个别异常组件带来的影响,且无法定位异常组件,因此目前的研究尚不能应用到实际中。通常情况下,异常组件的发电效率显著低于正常组件,识别效率低下的组件对运维工作具有指导意义,但目前关于组件、组串的能效指标的研究较少,能效优劣的界限模糊,难以给运维提供准确的指导意见[15-19]。
系统能效(Performance Ratio,PR)表示光伏电站的发电效率,其值用RP表示,RP等于光伏电站某时段内等效利用小时数与光伏组件倾斜面峰值日照小时数的比值[20-21],本文参考RP计算公式定义组件RP计算式,利用组件监测技术的优势,分析电站中各组件的实际运行数据,统计组件实际RP与理论RP的差值,对其进行假设检验,识别能效显著降低的组件,量化其差异程度,并利用量化值对组件工况进行简单分类,实现光伏组件的在线异常识别。
1 组件能效值及其分布
1.1 组件能效值
光伏电站常用RP,sta衡量整个电站的能效:
式中:Esta为电站输出电能;CI,sta为电站装机容量;∑Gsta为电站总辐照量;G0为标准测试条件下的太阳辐照强度,G0=1 kW/m2。
通常情况下,组件光电转化效率为14%~20%,并不能直观地表示组件效率的高低[22],而RP为实际发电量与理论发电量之比,故本文参考RP公式定义了组件效率的计算方式:
式中:RP,mod,r为组件在某时间段内的实际效率;Pr·i为第i个采样时刻的组件实际输出功率;ΔT为采样周期;Pstc为组件标称功率;Gi为第i个采样时刻的组件正面太阳辐照强度;n为采样点总数。
光伏组件输出功率受到太阳辐照强度与组件温度的影响,在不考虑其他因素的影响下,组件最大输出功率Pm为[23-26]:
式中:Tc为组件表面温度;Umref为组件标称电压;Imref为组件标称电流;Tref为标准测试条件下的组件表面温度,Tref=25 ℃;e 为自然对数底数;a,b,c参数选取推荐值[26]:a=0.002 5/℃,b=0.5 m2/W,c=0.002 88/℃。
则光伏组件理论RP,mod,t为:
式中:RP,mod,t为组件在某时间段内的理论效率;Pt·i为第i个采样时刻的组件理论输出功率;若令n=1,根据1 d 内所有数据采样点计算出各时刻的RP,mod,r,RP,mod,t,其差值ΔRP=RP,mod,r-RP,mod,t,在正常情况下,ΔRP在0 值附近变动,当ΔRP显著小于0时,表明组件能效值较低,此时组件出现了异常情况。
1.2 能效差值统计直方图
为识别能效显著降低的组件,引入统计假设检验,而分析对象服从正态分布是进行假设检验的前提,现根据电站运行数据,对某个组件1 d 中所有采样时刻的ΔRP进行统计分析,其直方图如图1 所示。图1 纵坐标“次数”表示在多次抽样中组件能效差值落在某个数值区间内的次数。由图1 可知,该组件的ΔRP服从正态分布。随着天气变化,ΔRP的分布情况也随之改变,如图2 所示,多云天气时,云层遮挡导致组件RP偏大或偏小,ΔRP的分布较为分散;晴天时云层较少,故ΔRP的分布较为集中。
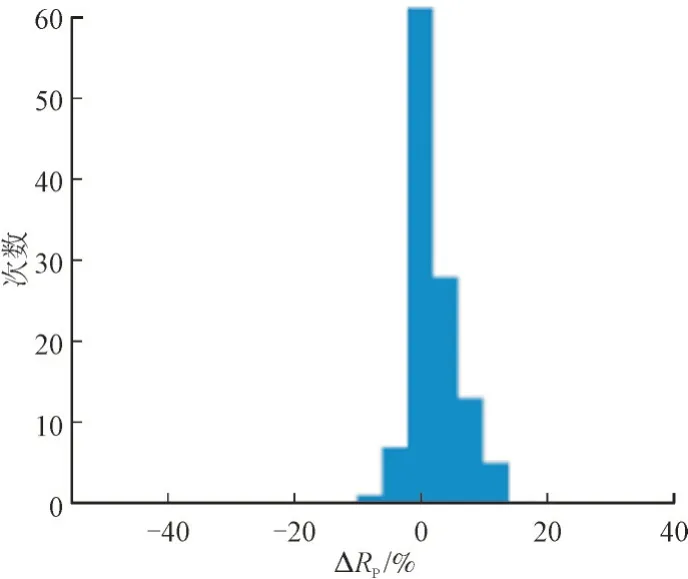
图1 ΔRP 直方图Fig.1 Statistical histogram of ΔRP

图2 不同天气组件ΔRP 直方图Fig.2 Statistical histogram of ΔRP for different weather components
2 基于t-检验与3-σ 检验的能效分析方法
2.1 t-检验与3-σ 检验
假设检验与参数估计是经典统计学中统计推断的2 个组成部分,假设检验是对总体参数提出一个假设并利用样本信息去检验该假设是否成立的一种方法[27]。
对组件电压、电流、环境辐照度的一次数据采集可看作对总体的一次抽样,各样本之间互不影响,现设原假设H0为组件实际能效值与理论能效值之差的均值大于或等于零,即组件能效正常;备择假设H1为组件实际能效值与理论能效值之差的均值小于零,即组件能效显著降低,即H0:μ(ΔRP)≥0,H1:μ(ΔRP)<0,其中ΔRP为组件实际能效值与理论能效值之差,μ为假设的总体均值,引入统计量t,设x1,x2,…xn是来自正态分布N(μ,σ2)的一部分样本,σ为电站中所有组件能效的标准差,则有:
式中:xj为第j个样本个体;为样本平均数;S2为样本方差;S为样本标准差;m为样本数量。
通过自由度m-1 和显著性水平α查找t分布表得到标准t值,若t<t(α,m-1),则拒绝原假设;否则不拒绝原假设。
在假设检验中,显著性水平α的含义为:当原假设正确时却被拒绝的概率或风险[27],一般α取0.05 或0.01,但由于实际工程中分析对象的情况各不相同,α须根据实际情况选取合适的数值。
根据t推断的结果进行决策所面临的风险是笼统的,为了更精确地反应决策风险度,常利用P值来代替检验统计量进行统计推断[11],P为原假设成立时抽到该样本或抽到更为极端的样本的概率,计算方式为:
式中:Gam(x)为伽玛函数;v为积分变量。
P>α时,不能拒绝原假设,说明组件能效值与理论能效值的差异并不显著;P<α时,根据小概率原理拒绝原假设,说明组件实际能效值与理论能效值差异显著,即组件能效值显著下降,此时应根据下降的程度对组件进行相应的维护。当P值取值范围在[0,1],当组件能效正常,P值接近于1,随着组件能效值的降低,P值逐渐减小并接近于0,故可根据P值的大小大致判断组件所处的情况,指导运维人员进行维护。
为区分出积灰和故障,识别能效显著低于平均值的组件,引入3-σ检验,易知在相同环境下各正常组件输出功率值服从正态分布,则其中99.73%的组件的能效值分布在在μ±3σ范围之内,当组件能效值低于μ-3σ时,认为该组件能效异常,其中μ为电站中所有组件的能效平均值。
2.2 分析方法
根据3-σ检验与t-检验结果,可对组件工况进行划分,如表1 所示,当t-检验和3-σ检验结果都为异常,说明该组件能效值低于理论值和平均值,此时应为单个组件异常;而当t-检验结果异常、3-σ检验结果正常,则说明该组件能效值低于理论值但与平均值相差较小,说明此时光伏阵列受到积灰、限功率等因素影响。

表1 利用2种检验方法对组件工况分类Table 1 Classification of component operating conditions using two inspection methods
当组件出现短路、断路等情况时,ΔRP较大,此时计算得出的P值极小,不利于分析,且此时的决策风险几乎为0,故定义d值表示组件实际能效值与理论能效值的差异程度,如下:
d值随着组件能效值的下降而增大,则可在P值较小的情况下根据d值的大小对组件的能效情况作出判断。
由于组件能效值受到天气因素的影响,降雨之后组件能效值上升,扬沙之后组件能效值下降[24-26],故选取一天中所有时刻的能效值进行t-检验,选取阵列中各组件当天的能效值进行3-σ检验。根据现有光伏电站运行数据进行分析,考虑到电站易受组件积灰的影响,选取显著性水平为0.005,该电站运行11 年,功率衰减至初始水平的75%,根据不同情况对组件工况进行划分,流程图如图3 所示。

图3 方法示意图Fig.3 Method diagram
考虑到组件在实际运行过程中可能有2~3 种工况共同存在的情况,例如热斑与积灰,此时应利用3-σ检验识别出异常组件,再根据其他组件的d值与该组件d值的差值Δd进行判断。
3 实验方法及分析
3.1 实验过程
现对本文方法进行验证,实验所用电站为北京某2.58 MWp 屋顶光伏电站,其光伏组件参数如表2所示。
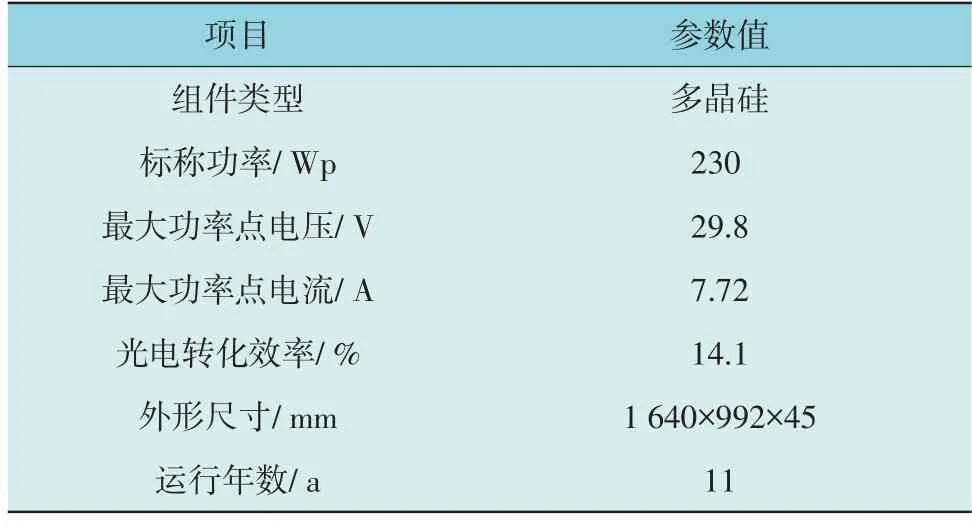
表2 组件参数Table 2 Component parameters
其气象数据由电站的气象站收集,组件配备电压、电流、温度传感器,每5 min 将数据收集并传输到后端平台。实验共分为4 种,分别为组件遮挡实验、组件短路和断路实验、组件碎裂和热斑实验、组件积灰实验,其中遮挡实验包括单子串50%,70%,100%,双子串50%,70%,100%,三子串50%,70%,100%共9 种情况,积灰实验包括积灰密度9g/m2,15g/m2,27g/m2共3 种情况,各实验步骤如下:
1)组件遮挡实验:(1)用拖布对组件进行清洁;(2)将纸壳按相应的尺寸、位置覆盖在组件正面,用胶布将其固定;(3)记录组件编号,观察其电压、电流、能效值变化情况;(4)撤去纸壳。
2)组件短路(断路)实验:(1)用拖布对组件进行清洁;(2)将组件引出线短接(断开);(3)记录组件编号,观察其电压、电流、能效值变化情况;(4)接线复原。
3)组件碎裂、热斑实验:(1)选取发生碎裂、热斑的组件,记录组件编号;(2)观察其电压、电流、能效值与其他正常组件的差异。
4)组件积灰实验:(1)用拖布对组件进行清洁;(2)根据不同的积灰密度分别将尘土覆盖在不同组串中所有组件正面表面;(3)记录组件、组串编号,观察其电压、电流、能效值变化情况。
实验情况如图4 和图5 所示。

图4 组件积灰实验示意图Fig.4 Schematic diagram of ash deposition experiment on component

图5 组件实验示意图Fig.5 Schematic diagram of component experiment
3.2 结果与分析
组件遮挡、故障实验时间为2023 年2 月18日-2023 年3 月8 日,组件积灰实验时间为2023 年3 月16 日-2023 年3 月19 日,每天8:00—18:00,各实验皆分为2 组,组一用于确定阈值,组二用于验证方法的正确性。由于传感器精度各不相同,剔除辐照度小于100 W/m2的数据,组一的实验结果如表3 所示。

表3 组一实验结果Table 3 Experimental results of group 1
由表3 可知,d值可以较好地反映组件的能效状况,该值并未严格地随着工况的异常程度的加深而增大,其原因可能是受到了外部环境以及组件衰老程度不一致等因素的影响。在异常工况下,ΔRP的分布情况如图6 所示。

图6 不同工况下的直方图Fig.6 Statistical histograms under different working conditions
由图6 可知,异常工况下组件当日ΔRP的直方图发生明显的偏移,图6 中个别异常值主要由组件和辐照仪受到云层遮挡导致,而当灰尘被清扫之后,ΔRP的分布图移动到0 值附近,表明灰尘清扫使得组件的发电效率有所提升的这一现象在直方图中有所体现,故亦可根据组件当日ΔRP直方图的分布情况判断组件所处的状态。
现根据组一的数据确定阈值,流程如图7 所示。

图7 组件能效统计分析流程图Fig.7 Flow Chart of energy efficiency statistics and analysis of component
按该方式对组二实验计算所得的组件d值与Δd值进行分类,如表4 所示。

表4 组二实验结果Table 4 Experimental results of group 2
由表4 可知,该方法可对组件工况进行简单分类,但热斑未能识别,分析该组件输出电压、电流,未发现明显低于其他组件的情况,推测可能是该组件热斑效应的程度较轻导致。
4 结论
本文提出了光伏组件能效计算方法,利用组件实际能效值与理论能效值之差进行假设检验,识别异常组件,结合t-检验量化值与3-σ准则对组件工况进行了简单分类,提出了一种基于经典统计推断的组件能效分析方法,实现光伏组件异常识别。通过对本文提出的方法进行典型故障及积灰实验验证,得到以下结论:
1)光伏组件的发电效率可用组件能效值来衡量。
2)本文提出的假设检验方法可以有效识别能效显著降低的组件。
3)通过本文提出的d值可以较好地衡量光伏组件能效的优劣程度。
4)结合d值与3-σ检验可以在一般情况下对组件工况进行分类。
5)本文提出的基于经典统计推断的组件能效分析方法亦可用于识别能效异常的组串。
本文仅根据少量实验结果对组件不同工况划分了d值的大致范围,尚需根据大量实验数据进行修正。
