考虑VSC与光-储-充协同配置的交直流混合配电网规划
2023-12-05朱建昆高红均贺帅佳刘俊勇
朱建昆,高红均,贺帅佳,江 均,刘俊勇
(1.四川大学电气工程学院,四川成都 610065;2.国网四川泸州供电公司,四川泸州 646000)
0 引言
近年来,随着“双碳”目标的提出以及新能源汽车的发展[1-4],我国光伏电站、储能与电动汽车直流充电站的配置容量不断增加。直流源储荷若直接接入传统的交流配电网中需要用户额外配置换流装置,这会极大增加用户的工作量,不利于直流源储荷的发展。而交直流混合配电网在网架结构[5]以及对直流源储荷的兼容性等方面的优势不断凸显,将成为未来配电网的重要形态[6]。在此背景下,引入考虑光-储-充协同配置的交直流混合配电网规划具有重要的意义。
目前国内外学者针对光-储-充的配置进行了大量的研究。在光伏电站与储能的配置方面,文献[7]以分布式光伏全年总发电量最大为目标,兼顾配电网经济性建立光储联合配置规划模型。文献[8]研究了分布式光伏接入配电网的选址定容。文献[9]在考虑光伏出力与负荷需求不确定性的基础上建立储能配置模型。在直流充电站配置方面,文献[10]提出了一种在备选站址既定的情况下含不同备选容量充电站的选址定容方法。文献[11]在模型中综合考虑了充电站规划运行成本与电网运行安全指标。但文献[7-11]主要集中在传统交流配电网,忽略了换流装置对于直流形式光-储-充并网的重要作用。因此有必要在交直流混合配电网中考虑换流转置进行光-储-充配置,充分发挥交直流混合配电网对直流源储荷的良好兼容性。
同时,对于交直流混合配电网的规划,文献[12]以最小化投资建设成本、运营成本、可靠性成本为目标,建立中压交直流混合配电网规划模型。文献[13]提出了一种交直流混合配电网双层规划模型,其中上层模型以投资成本和运行成本的综合成本最小为目标,下层模型以投资成本和运行成本的综合成本最小为目标。文献[14]以运行成本与配置成本最小化为目标提出了一种交直流混合配电网的随机规划模型。但文献[12-14]未考虑换流器件的选址定容问题。作为交直流混合配电网中的核心设备之一,换流器件对于电网的实际规划与运行的影响不可忽视。有必要将换流器件的选址定容融入交直流混合配电网的规划问题,完善规划模型。
另外,负荷的不确定性对于交直流混合配电网的规划具有重要影响。现阶段处理不确定性的方法主要有随机优化方法(Stochastic Optimization,SO)、鲁棒优化方法(Robust Optimization,RO)与分布鲁棒方法(Distributionally Robust Optimization,DRO)3 种。由于DRO 克服了SO 中部分随机变量概率分布参数难以获取以及RO 中决策结果过于保守的缺陷[11],近年来得到了广泛的关注,在电力系统的协同规划[12-15]、优化调度[16-22]等领域均有应用。基于此,本文采用DRO 处理直流负荷的不确定性,力求得到兼顾经济性与鲁棒性的交直流混合配电网规划方案。
因此,本文提出一种采用电压源型换流器(Voltage Source Converter,VSC)和电池储能系统(Battery Energy Storage System,BESS)的考虑VSC与光-储-充协同配置的交直流混合配电网多主体规划框架,构建各规划主体模型,使用基于多离散场景的DRO 方法将直流负荷的不确定性融入交直流混合配电网规划模型中,并采用列与约束生成(Column and Constraint Generation,CCG)算法进行迭代求解。随后在仿真算例中验证本文提出的规划方法的优越性。
1 适应光-储-充多投资运营主体的交直流混合配电网规划框架
本文规划目的是将交流配电网改造为交直流混合配电网,直流配电网与交流配电网之间通过VSC 装置互联,交流配电网上接有交流负荷,并通过变电站与上级电网相连。直流配电网上接有光伏电站、直流充电站、直流负荷以及储能。直流配电网电能来源于交流配电网中通过VSC 注入的电能以及直流配电网上接入的光伏电站与储能所提供的电能。
本文所采用的交直流混合配电网互动主体包括电网公司、光伏电站、储能运营商与直流充电站运营商。其中,电网公司作为领导者,需提供向运营商售电的分时电价与运营商向电网公司售电的电价信息;储能运营商、直流充电站运营商以及光伏电站则作为跟随者,根据电网公司提供的分时电价,以利润最大化为目标制定自身的规划运行策略,并将规划运行策略反馈回电网公司。
2 考虑VSC 与光-储-充协同配置的交直流混合配电网规划模型
2.1 电网公司
2.1.1 目标函数
1)规划层:对于电网公司而言,规划层的目标函数为交直流混合配电网规划总成本finv最小。
2)运行层:运行层的目标函数为交直流混合配电网规划后的效益最大化。
2.1.2 约束条件
1)变电站传输功率约束为:
2)换流器件约束。本文采用文献[22]中换流器件约束进行规划,在此不再进行详细阐述。
3)线路潮流约束。本文采用文献[23]中经二阶锥松弛后的交直流Distflow 模型进行规划,在此不再进行详细阐述。
4)节点电压约束为:
5)设备选型约束为:
该约束能够保证线路只能在给定的候选型号中选择一种型号进行投资。
6)投资数量约束为:
式中:ΩVSC,type为VSC 机组的安装候选型号集合;SVSC,max为VSC 机组的最大投资数量。
2.2 光伏电站
2.2.1 目标函数
对于光伏电站的投资商而言,目标函数为光伏电站的年利润最大化。
2.2.2 约束条件
1)光伏机组出力约束为:
2)设备选型约束为:
3)投资数量约束为:
式中:SPV,max为光伏机组的最大投资数量。
2.3 隶属于储能运营商的BESS
2.3.1 目标函数
对于储能运营商而言,目标函数为BESS 的年利润最大化。
2.3.2 约束条件
1)BESS 的充放电约束。本文采用文献[18]中BESS 运行约束条件进行规划,在此不再进行详细阐述。
2)设备选型约束为:
3)投资数量约束为:
式中:SBESS,max为储能的最大投资数量。
2.4 直流充电站运营商
2.4.1 目标函数
对于直流充电站运营商而言,目标函数为直流充电站的年利润最大化。
2.4.2 约束条件
1)直流充电桩出力约束为:
式中:PDCEV,max为直流充电桩充电功率的上限。
2)设备选型约束
3)投资数量约束为
式中:SDCEV,max为直流充电站中直流充电桩的最大投资数量。
3 不确定性处理与模型求解算法
3.1 不确定性处理
针对直流负荷的不确定性,本文采用基于多离散场景的DRO 方法,通过引入波动系数αload,DC来建立不确定集合U:
该集合表征了直流负荷波动的上下限。根据不确定集合U随机生成N个场景并聚类出Ns个离散场景,构建基于1-范数和∞-范数约束概率分布波动范围的DRO 模型[24].
基于多离散场景的DRO 模型的目标函数可表示为:
s.t.式(5) —式(9)式中:x为规划层决策变量;X为规划层决策变量集合;Ps为场景s的发生概率;ys为运行层决策变量;Ys为运行层决策变量集合;Ns为离散场景数量。
DRO 模型的概率分布置信集合ψ可表示为:
3.2 模型求解算法
考虑到光伏电站、储能运营商与直流充电站运营商具有独立的运营策略,本文将光伏电站、BESS与直流充电站的规划与交直流混合配电网的规划分离。具体而言,对于前三者规划采用CPLEX 进行求解,而对于交直流混合配电网规划中的DRO模型,本文采用CCG 算法进行求解,具体流程如图1 所示。

图1 本文求解算法流程图Fig.1 Flow chart of solving algorithm for proposed model
图1 中UB 和LB 分别为迭代上界和迭代下界,+∞为正无穷,为第m+1 次迭代下场景s的发生概率。
4 算例分析
本文在文献[25]的148 节点系统的基础上采用修改后的75 节点系统作为算例对象的交流配电网部分,其具体的拓扑结构如图2 所示。此外,算例拟在原有的75 节点的交流配电网基础上接入7 节点的直流配电网,从而将原有的交流配电网改造为交直流混合配电网,直流配电网的拓扑结构如图3 所示,图3 中x与y分别为直流节点间的横向与纵向距离。算法采用MATLAB 2016b 编写,并调用CPLEX12.6求解。
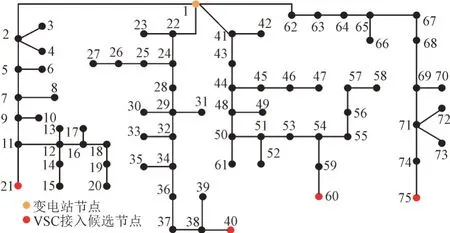
图2 75节点拓扑结构图Fig.2 Topology sturcture for 75-node system

图3 直流配电网拓扑结构图Fig.3 Topology structure for DC distribution network
4.1 模型参数说明
为实现交直流混合配电网的规划,算例拟在不同位置配置2 台VSC,同时在直流配电网中配置光伏电站、储能与直流充电站。设定直流配电网为两端配电型拓扑结构,直流配电网中的1 号与7 号节点为首末节点,其余节点间通过配置直流线路实现电能传输,且单个节点只能与2 条线路间实现电能交换。详细参数如表1 所示。
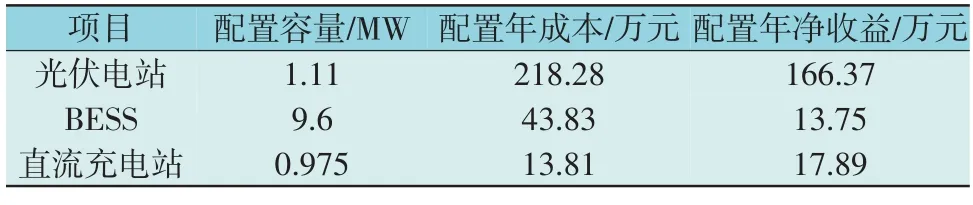
表1 光-储-充规划结果Table 1 Planning results of photovoltaic-storage-charging
交直流混合配电网的规划网架结构为1-5-3-2-4-6-7,线路规划的年成本为24.42 万元,具体结果如表2与图4所示。

表2 交直流混合配电网规划结果Table 2 Planning results of AC/DC hybrid distribution network

图4 各时段电网功率示意图Fig.4 Schematic diagram of electric network power for each time period
由图4 知,由于BESS 充电,交直流混合配电网中由交流配电网经VSC 流向直流配电网的净有功功率在04:00—05:00 期间有明显的上升,随后得益于光伏发电功率的提升,净有功功率在缓慢下降。在09:00—11:00 期间由于交流电网的负荷迅速上升,变电站传输功率出现了明显的上升,在16:00—20:00 期间传输功率出现了进一步的上升,这是由于“晚高峰”期间交流电网的负荷有了进一步的上升,并且交流电网还需向直流电网送电,两者叠加进一步提高了传输功率。在22:00 时BESS 的状态由放电变为以最大充电功率进行充电,此时流向直流配电网的净有功功率达到峰值。
4.2 模型对比分析
4.2.1 VSC配置台数对VSC选址定容影响分析
4.1 节中VSC 的配置台数均为2 台,作为对比,提出以下场景进行验证:(1)场景1:本文所提出的规划方法,即配置2 台VSC;(2)场景2:配置3 台VSC,其余条件与场景1 相同;(3)场景3:配置4 台VSC,其余条件与场景1 相同。
表3 为不同VSC 配置台数的规划结果,显示场景1、场景2 和场景3 的VSC 配置容量为配置2台、3 台和4 台VSC 时各台VSC 的具体容量。由表3,随着VSC 配置台数的增加,每台VSC 配置的容量在逐渐减少,但由于VSC 固定成本随VSC 配置台数的增加而增加,因而VSC 配置的年成本也在逐渐增加。

表3 不同VSC配置台数规划结果Table 3 Planning results for different VSC configurations
考虑到配电网负荷的逐年增长将对配电网实际运行产生不可忽视的影响,表4 展示了在规划后5 年,10 年,15 年后配电网交流侧主干线路有功功率的最大值与标准差,定义主干线路为VSC 接入候选节点与变电站之间最短路径所包含的线路。由表4 知,尽管随着VSC 配置台数的增加,主干线路有功功率最大值与标准差有着一定程度的改善,但由于模型中对主干线路有功功率的预留裕度较为充足,这些改善并未明显体现于配电网运行结果中,不足以弥补额外付出的配置成本。因此在满足电网运行的安全性前提下,相较于场景2 与场景3,场景1 具有更好的经济性。
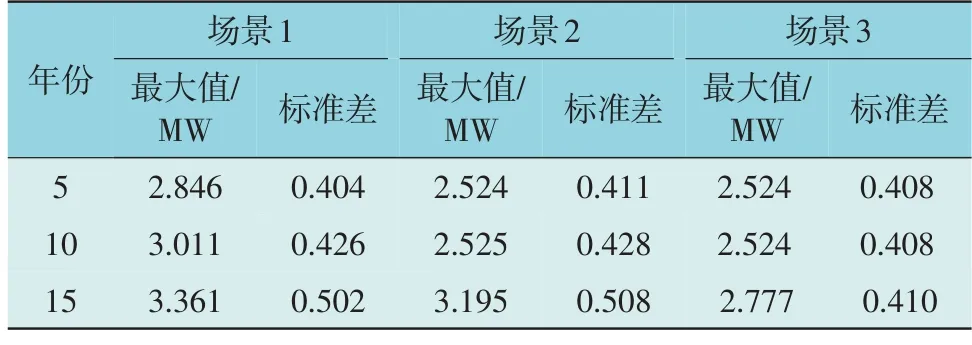
表4 规划后不同年份主干线路有功功率的最大值与标准差Table 4 Maximum value and standard deviation of active power of trunk lines with different durations after planning
4.2.2 不确定性对比分析
本文采用基于多离散场景的DRO 方法来处理直流负荷的不确定性,作为对比,提出以下场景进行验证:(1)场景4:采用随机优化方法来处理直流负荷的不确定性;(2)场景5:采用鲁棒优化方法来处理直流负荷的不确定性;(3)场景6:采用基于多离散场景的DRO 方法来处理直流负荷的不确定性,但αDCload取0.2.
具体仿真结果如表5 所示,场景1 的年总运行成本处于场景4 与场景5 之间,原因为DRO 方法能够在经济性与鲁棒性之间进行一定范围的动态调整,使之更加贴合实际运行情况。而根据场景1与场景6 的对比,随着不确定性波动系数的增加,直流负荷的波动愈发剧烈,CCG 算法的二阶段产生的概率分布也就愈发恶劣,年总运行成本也在逐渐增加。

表5 不同不确定性处理方法运行结果Table 5 Running results of different uncertainty handling methods 万元
5 结论
本文提出一种考虑VSC 与光-储-充协同配置的交直流混合配电网规划模型,计及直流负荷的不确定性并采用CCG算法进行求解,结论如下:
1)本文所提模型能够充分利用VSC 在交流配电网与直流配电网间进行能量交互,兼顾了投资经济性与电网运行的安全性。
2)提高VSC 配置台数能够有效改善主干线路的负荷均衡度,并减少单台VSC 机组的配置容量,但固定成本的增加会导致总投资成本的上升。因此,决策时应根据实际情况与需求灵活选择VSC配置台数。
3)本文采用DRO 方法处理直流负荷的不确定性,能够兼顾规划的经济性与鲁棒性。此外,随着直流负荷不确定性的增强,DRO方法规划的鲁棒性变强,规划的经济性则会降低。
本文只考虑了光-储-充与电网公司之间的交互,下一步将考虑光-储-充之间的交互关系,从而准确刻画各运营商之间的交互行为,进一步完善交直流混合配电网的规划工作。
