多路阀阀芯节流槽拓扑结构的优化设计
2023-12-04付松松李卫民
付松松,李卫民
(辽宁工业大学机械工程与自动化学院,辽宁锦州 121001)
0 前言
多路阀作为工程机械液压控制系统中的核心控制元件之一,能够实现多执行机构同时工作,故被广泛应用于工程机械中[1-2]。其性能要求为换向过程的稳定性及可靠性,液动力是影响换向阀性能的重要因素之一[3-4]。流体流过滑阀阀口时,由于流动方向及流速的变换引起动量的变换,所以阀芯受到附加轴向力,即液动力。
为了提高多路阀的换向性能,许多学者通过理论、试验或仿真手段对液动力展开了研究。张宏等人[5]应用仿真手段,验证了数值模拟的正确性,并指出采用Realizableκ-ε模型能够更好地拟合试验数据。郑长松等[6]通过理论分析,结合应用Fluent仿真软件得到滑阀不同开度下的稳态液动力结果,得到了稳态液动力的修正计算公式。邓斌等人[2-7]通过AMESim与Fluent的联合仿真,分析了稳态液动力随着阀口开度的变化趋势,并指出在计算阀芯操纵力时,不能忽略稳态液动力;基于Fluent数值仿真,通过拟合得到射流角与阀口开度的公式,建立了稳态液动力数字化计算模型,对渐扩形U形节流槽进行优化设计。王安麟等[8]以试验为基础,基于流固耦合,分析不同节流槽下的流固耦合动力学响应。综上,多数学者均对稳态液动力变换规律及理论修正进行了研究,但针对节流槽结构尺寸变化对稳态液动力的影响研究较少。
为进一步改善稳态液动力对多路阀阀芯操控性能的影响,提高多路阀的换向性能,以降低该过程的稳态液动力为目标,本文作者采用数值仿真分析方法,基于ANSYS建立阀芯与阀体热流固耦合三维求解模型,通过可视化分析半圆形节流槽阀芯下的流动状态,提出新型节流槽拓扑结构,并建立Non-parametric Regression响应面模型,研究新型节流槽结构尺寸对稳态液动力与流量的影响。结合多目标遗传算法(Multi-Objective Genetic Algorithm,MOGA)寻优求解,并对比分析优化前后流动状态及阀芯所受稳态液动力等。
1 数值模型的建立
文中多路阀阀芯节流槽拓扑结构处于流场、温度场和结构场的多物理场耦合作用下,因此需要建立各场控制方程以及热流固耦合方程。
1.1 流体控制方程
连续性方程为
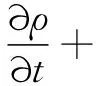
(1)
动量守恒方程为
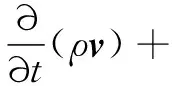
(2)
式中:f为体积力矢量;t为时间;v为流体速度矢量;ρ为流体的密度;τ为剪切力张量。
1.2 固体控制方程
可根据牛顿第二定律推导出固体的守恒方程:
ρa=∇σ+f
(3)
式中:a为当地加速度矢量;σ为柯西应力张量。
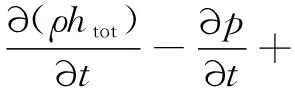
∇·(V·τ)+v·ρff+SE
(4)
其中:htot为显焓;p为压力;V为体积;SE为能量源项;λ为导热系数。
对于固体部分,增加了由温度引起的热变形项:
fT=αT·∇T
(5)
其中:αT为与温度相关的热膨胀系数。
1.3 流固耦合方程
流固耦合属于固态和液体之间的相互作用,它同时也遵守能量守恒原则。在流固耦合交界面上,需要保证流体和固体应力τ、位移d等参数相等或守恒,可表达为下列方程式:
(6)
式中:下角标f表示流体,下角标s则表示固体。
1.4 计算方法
文中热流固耦合[9]的计算步骤如下:
(1)利用ANSYS数值仿真分析平台搭建流体场、温度场及结构场间的联系,通过Fluent数值仿真求解;(2)将流体场温度计算数据导入固体温度场Steady-State Thermal,进行固体温度场求解;(3)将流体压力计算数据及温度场温度计算数据导入结构场Static Structural,进行结构场求解。求解过程如图1所示。

图1 热流固耦合求解过程Fig.1 Heat-fluid-structure coupling solution process
2 仿真模型及边界条件
多路阀由多联换向阀体构成,每联阀体主要由阀芯与阀体构成,通常阀芯上有不同形状的节流槽,通过合理组合节流槽,可获得对流量的多级控制,以适应不同工况下执行机构的需要。实际工况中应用的模型较为复杂,如图2所示,由于此研究主要针对半圆节流槽阀芯换向时所受稳态液动力的影响,因此为了减少不必要的计算,对模型进行简化,省略多路阀中的其余零件,如图3所示。
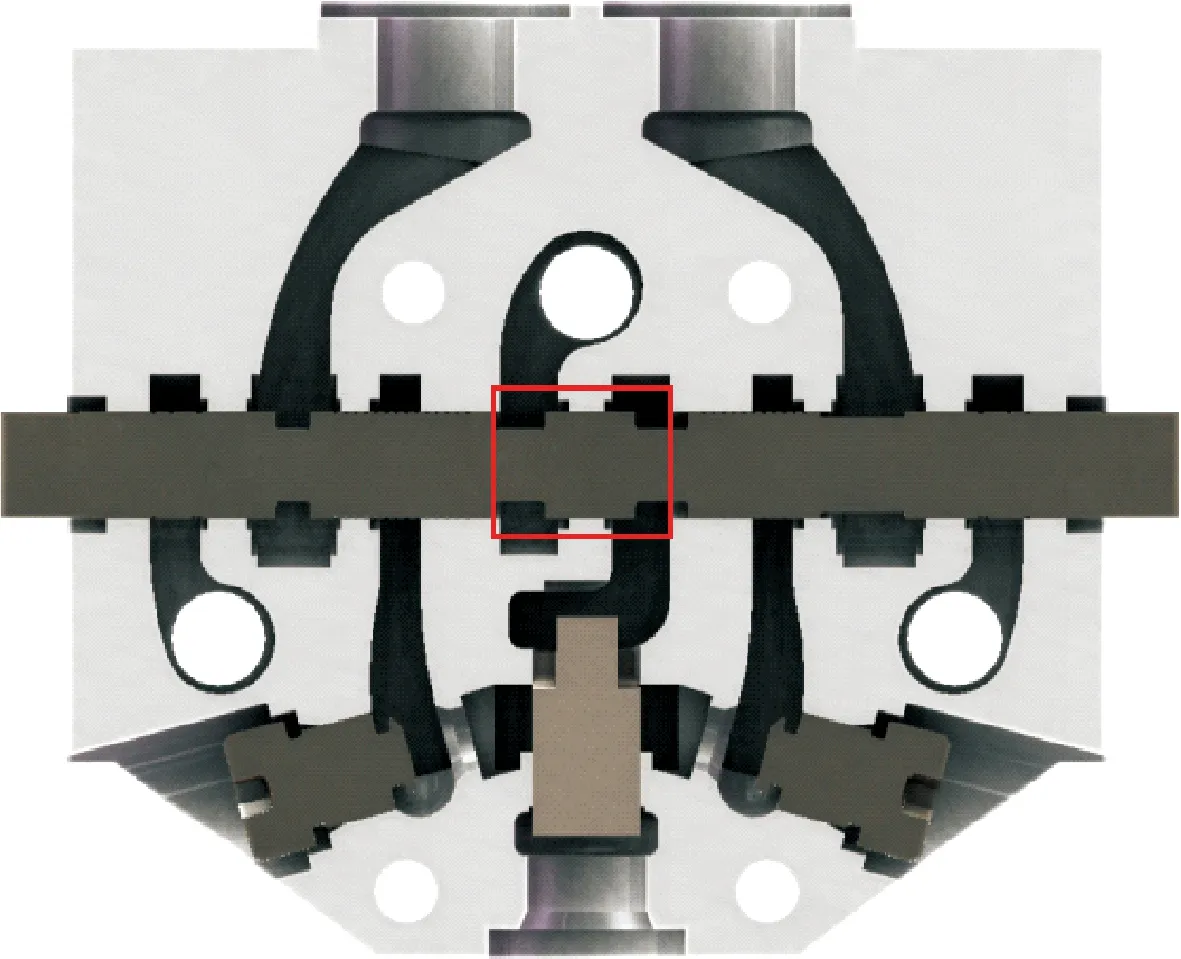
图2 多路阀单联三维数字模型Fig.2 Multi-way valve monolithic 3D digital model
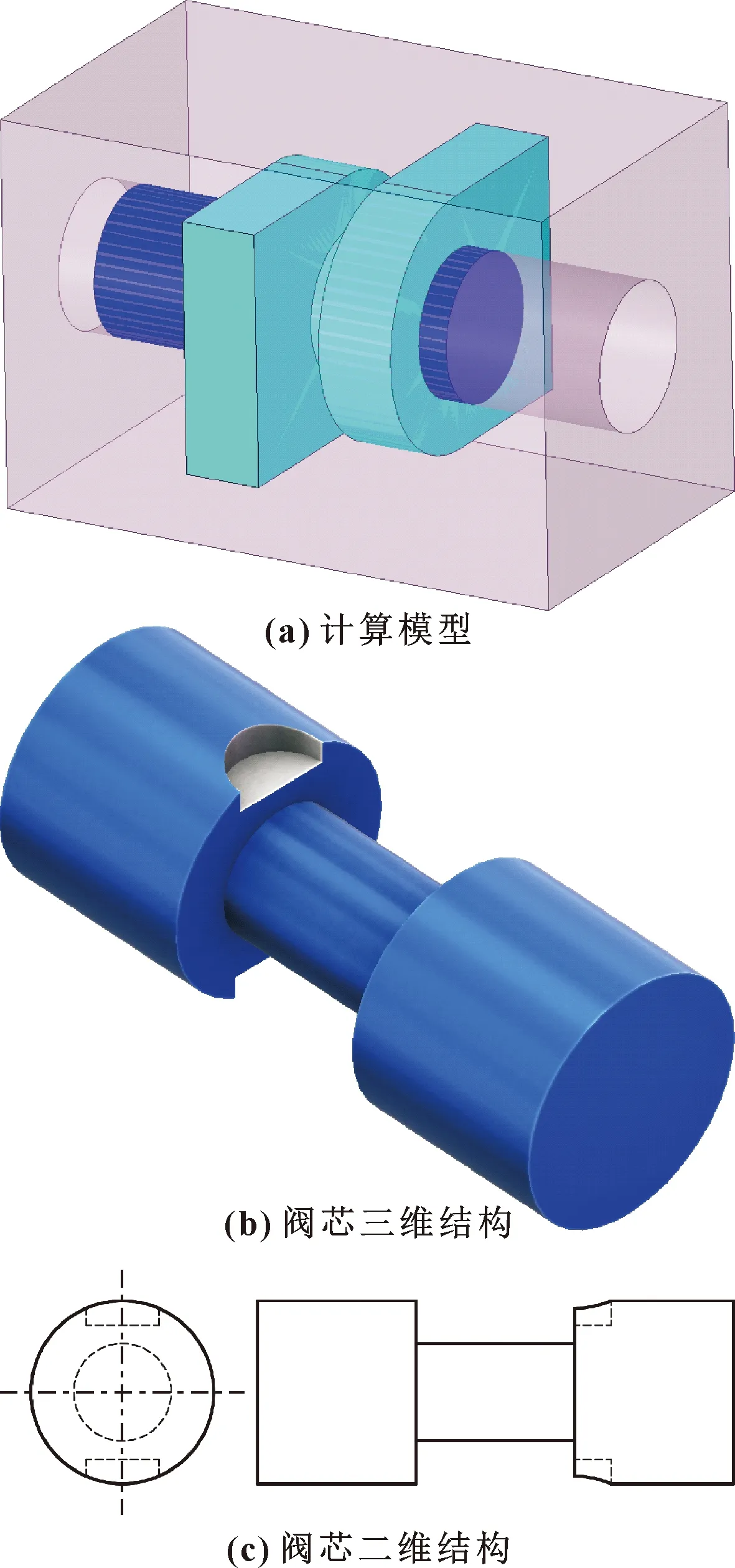
图3 简化模型Fig.3 Simplified model:(a)computational model;(b)3D structure of valve core;(c)2D structure of valve core
2.1 介质属性
基于ANSYS数值仿真分析建立阀芯与阀体热流固耦合分析,所需的液压油、阀芯与阀体的物理参数如表1、2所示。对流体特性及流动状态做以下假设:流体为不可压缩和牛顿流体;由于流体的重力对此次模型影响不大,因此忽略重力的影响;油液黏度不随温度的变化而变化;阀芯与阀体间的配合良好,不考虑内泄的影响。

表1 ISOVG32液压油物理参数Tab.1 Physical parameters of ISOVG32 hydraulic oil

表2 固体材料参数Tab.2 Solid material parameters
2.2 流场边界条件
建立流体与固体间的数据共享(Mesh Interface),即共节点。采用非结构化网格进行网格划分,流体、固体全局网格最大为1 mm,并对流体域进行边界层的设置:边界层采用平滑变化形式,变化率为0.272,增长率为1.2,共4层。如图4所示,最终网格节点为117 353,单元为492 396。激活能量方程,采用Realizableκ-ε湍流模型进行求解,并打开黏性温升项(Viscous Heating)。边界条件进出口均为压力边界条件,入口压力为6 MPa,出口压力为5 MPa,即压差为1 MPa。假设温度环境为30 ℃,其中流固耦合面壁面类型为Interface,通过系统耦合方式进行热量的交换,其余壁面类型均为Wall。动量、湍流动能、湍流耗散率及能量均选择二阶迎风格式进行离散化,采用耦合式(Coupled)的计算方法,提高求解精度。残差收敛至10×10-6即为迭代收敛。

图4 流体域网格截面Fig.4 Fluid domain mesh section
2.3 固体边界条件
通过Engineering Data自定义添加阀体阀芯所需要的材料。阀芯与阀体设置为带摩擦的接触,摩擦因数设为0.04。固体全局网格最大为1 mm,最终网格节点为303 330,单元为203 124。设置固体与流体交界的内壁为流固交界面(Fluid Solid Interface,FSI),阀体外壁面添加对流换热。导入流场温度计算结果,通过耦合求解器进行温度场求解。固体外壁面添加固定约束,阀芯两端添加Remote Displacement约束。导入温度场温度计算结果和流场压力计算结果,通过耦合求解器进行结构场求解。
3 仿真结果分析
通过上述热流固耦合对所研究模型进行多物理场耦合求解,分析不同开度下阀芯受到的稳态液动力,如图5所示。
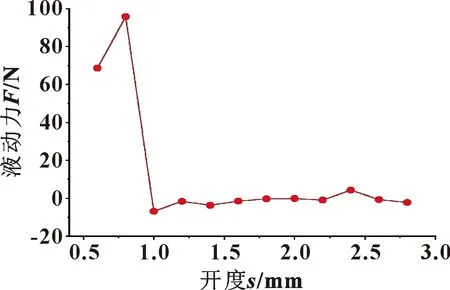
图5 不同开度下的稳态液动力Fig.5 Steady-state flow forces at different openings
由图5可知:阀芯开度较小时,其所受到的稳态液动力较大,且稳态液动力的方向为阻碍阀芯开启方向;随着开度的增加,阀芯所受到的稳态液动力减小,且力的方向与阀芯开启方向相同。由于换向阀性能要求滑阀移动换向的过程中可靠且稳定,故应降低阀芯开度较小时的液动力来增强其换向可靠性。
根据上述对阀芯所受液动力的分析,文中在此节流槽的基础上进行结构优化,且不改变原有滑阀行程,如图6所示。并基于响应面对新型结构进行多目标优化来获取其最佳尺寸。
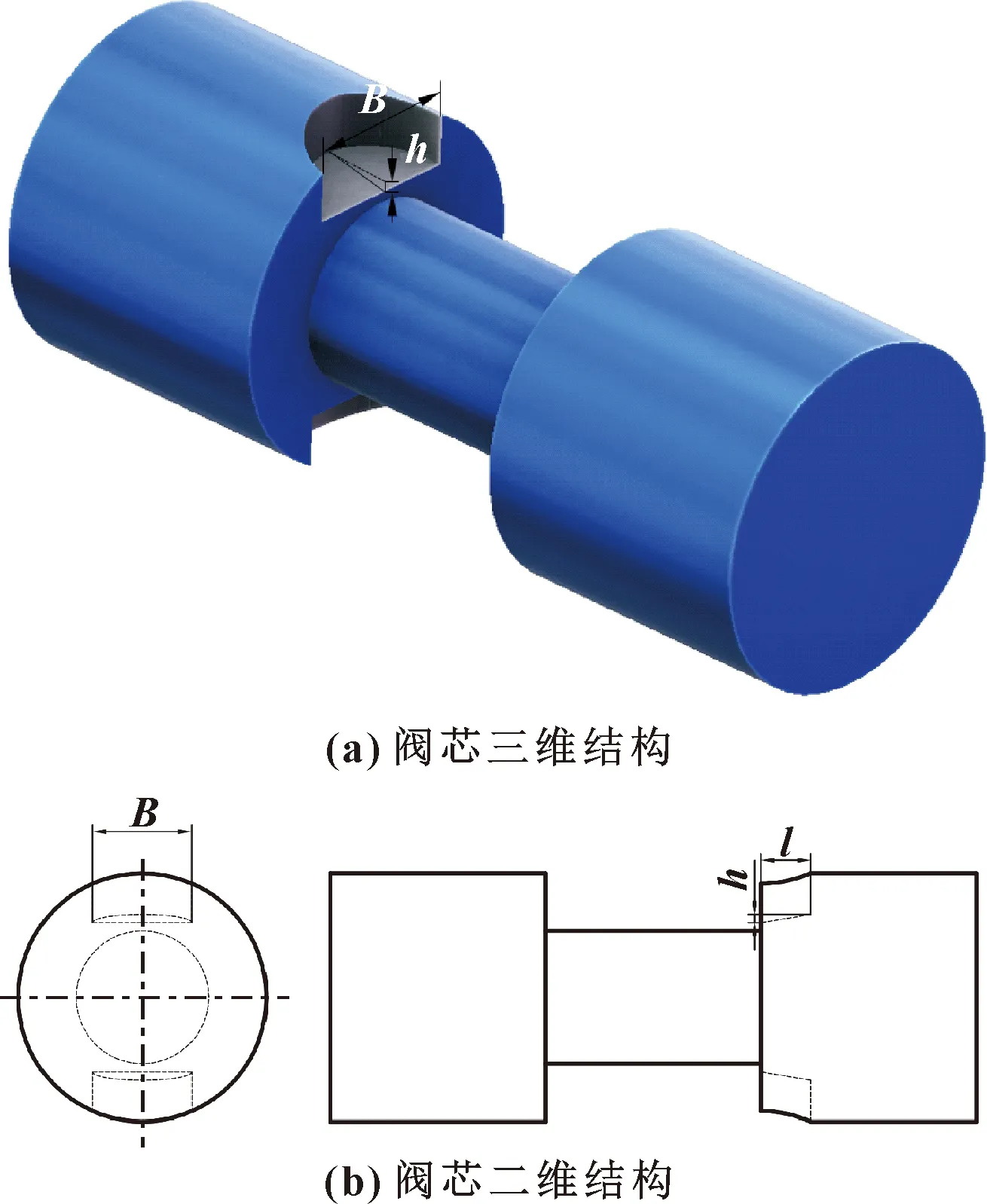
图6 新型节流槽结构Fig.6 New throttling groove structure:(a)3D structure of valve core;(b)2D structure of valve core
4 阀芯的多目标优化
4.1 设计变量的确定
滑阀阀芯是用来控制换向阀流体方向及流量的主要零件,近年来,非全周开口的阀芯更是在各大品牌多路阀中应用,它具有丰富的节流槽结构,可通过相互组合以满足客户所需要的运动状态。为了提高阀芯开启过程中的性能,以降低液动力为评判标准,选取节流槽宽度及坡度2个主要参数作为阀芯优化的设计变量,各变量变化范围如表3所示。

表3 设计变量优化区间Tab.3 Design variable optimization interval
4.2 抽样方法的选择
文中采用拉丁超立方体抽样法(Latin Hypercube Sampling,LHS)进行样本的采集。LHS是以概率统计为理论指导的计算方法,其核心思想是将问题转化为相应的概率模型,对概率模型进行相应的统计实验,最后的统计结果就是问题的近似解。文献[10]对比分析了蒙特卡洛法和LHS,结果表明LHS抽样方法所抽样本能更加准确地反映输入的概率分布,且具有更高的计算效率。
4.3 DOE实验设计
选取阀芯节流槽槽宽P1及坡度P2两个参数为试验设计的2个因子,实验中采用拉丁超立方体抽样设计,样本类型为CCD采样,以阀芯所受稳态液动力及流量作为量化的目标函数,试验结果如表4所示。
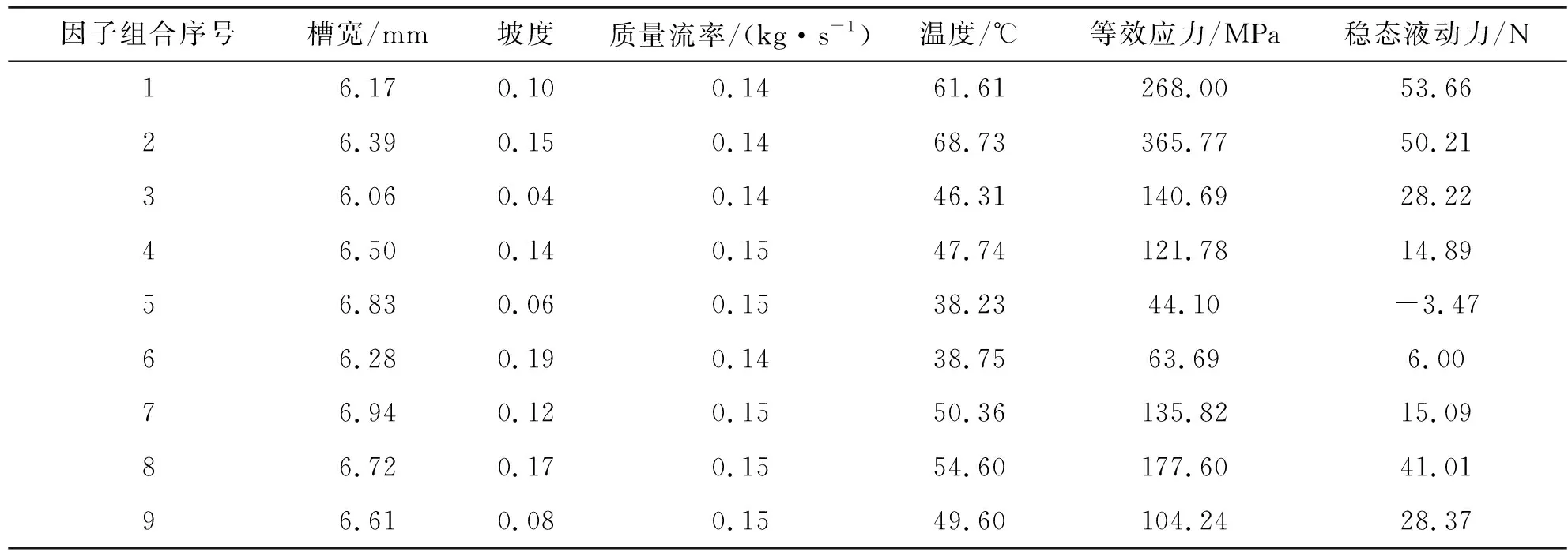
表4 样本数据点及结果Tab.4 Sample data points and results
4.4 响应面模型的构建
响应面分析法(Response Surface Methodology,RSM)是一种数理统计学方法[11],利用合理的设计方法及实验结果,采用多元二次回归方程拟合设计变量与响应关系的多项式方程,并用它代替物理模型进行优化与分析。
建立响应面模型时,输入变量x与输出变量y的函数关系可表示为
y=f(xn)+ε
(7)
一阶模型如下:
(8)
式中:y为输出变量(压力损失);β0为多项式常数项;βi为系数;k为输入变量总数;x为输入变量(P1、P2);ε为回归值与实际值的误差。
由一阶数学模型式(8)可知拟合函数为一次多项式,由泰勒多项式拟合曲线的定义可知高阶拟合函数更能逼近实际响应面,而随着阶数的增加其计算成本也将指数倍增加,因此采用二阶模型逼近实际响应面模型,既保证了精度要求,又减少了计算成本。其响应面二阶模型如下:
(9)
二阶模型是模拟真实极限状态的曲面,分析曲面可获得设计变量的响应面最优值,最终实现节流槽尺寸的优化设计。
采用Non-Parametric Regression(非参数回归)拟合响应面,通常以R2(判定系数)和RMSE(均方根误差)来评判响应面模型的准确性和适应性。R2能反映出方差分析得到的回归直线的拟合程度,它是y值的变异占y值的总体变异的比率,R2越趋近1,表示回归方程拟合得越好;相反地,R2越趋近0,表示回归方程拟合得越差。RMSE能够反映模型预测值与实验值的差异程度,其值越小,则响应面模型精度越高。表5所示为该回归拟合响应面模型的评判值。

表5 方差分析Tab.5 Variance analysis
基于上述评判可知,建立Non-Parametric Regression响应面可适合于所求解的问题,图7(a)为设计变量对质量流率的响应,图7(b)为设计变量对稳态液动力的响应。其中,三维散点为试验设计点,它基本附着于所建立的响应面之上,进一步表明该模型的可靠性。如图8所示,散点基本位于45°线的附近[12],也进一步说明响应面质量较好。
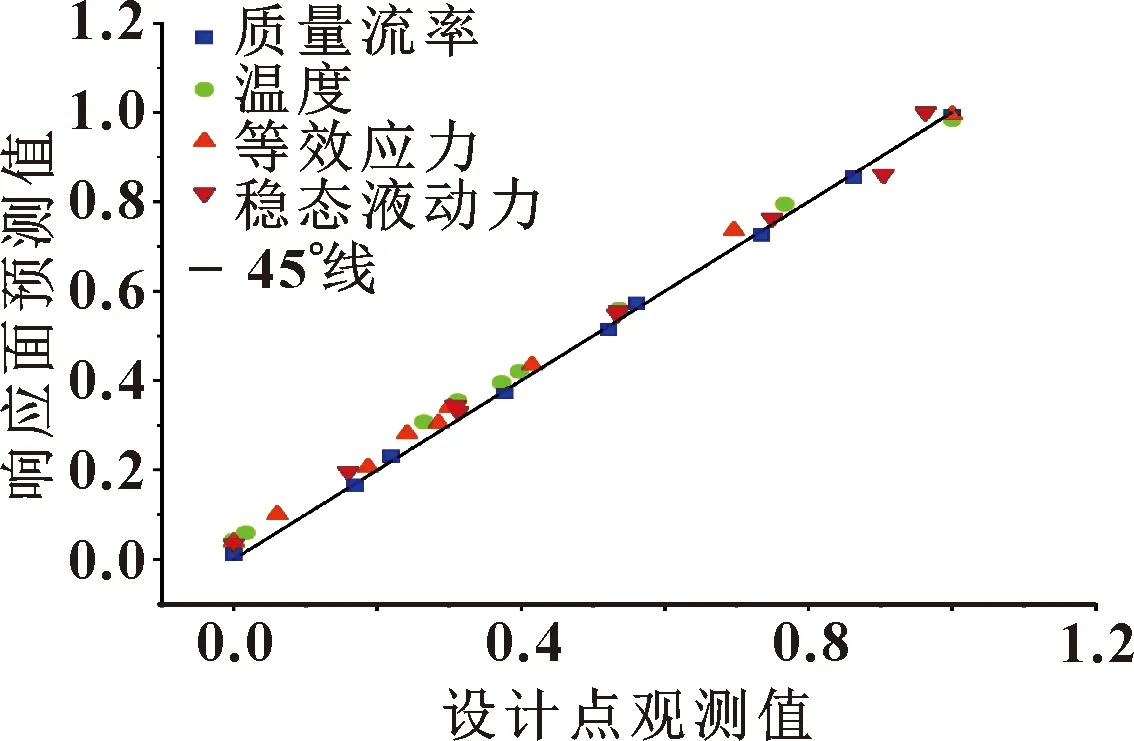
图8 拟合优度Fig.8 Goodness of fit
4.5 灵敏度分析
在进行结构优化设计时,所优化的目标通常是多个设计变量相互作用的结果。通过灵敏度分析可以得到设计变量对某一目标的影响程度,从而将影响较大的设计变量(一个或多个)作为关键变量进行设计。灵敏度在众多领域中均有涉及,其一阶灵敏度数学表达式为
(10)
式中:Δp表示设计变量的变化量。
灵敏度数值的大小表明设计变量对目标响应的响应程度,即设计变量对该目标的贡献率。如图9所示,对质量流率的响应中,设计变量P1的贡献率最大,且设计变量P1与P2均与响应变量成正相关;对温度、等效应力及稳态液动力的响应中,设计变量P1为主要影响变量,与响应变量成负相关。
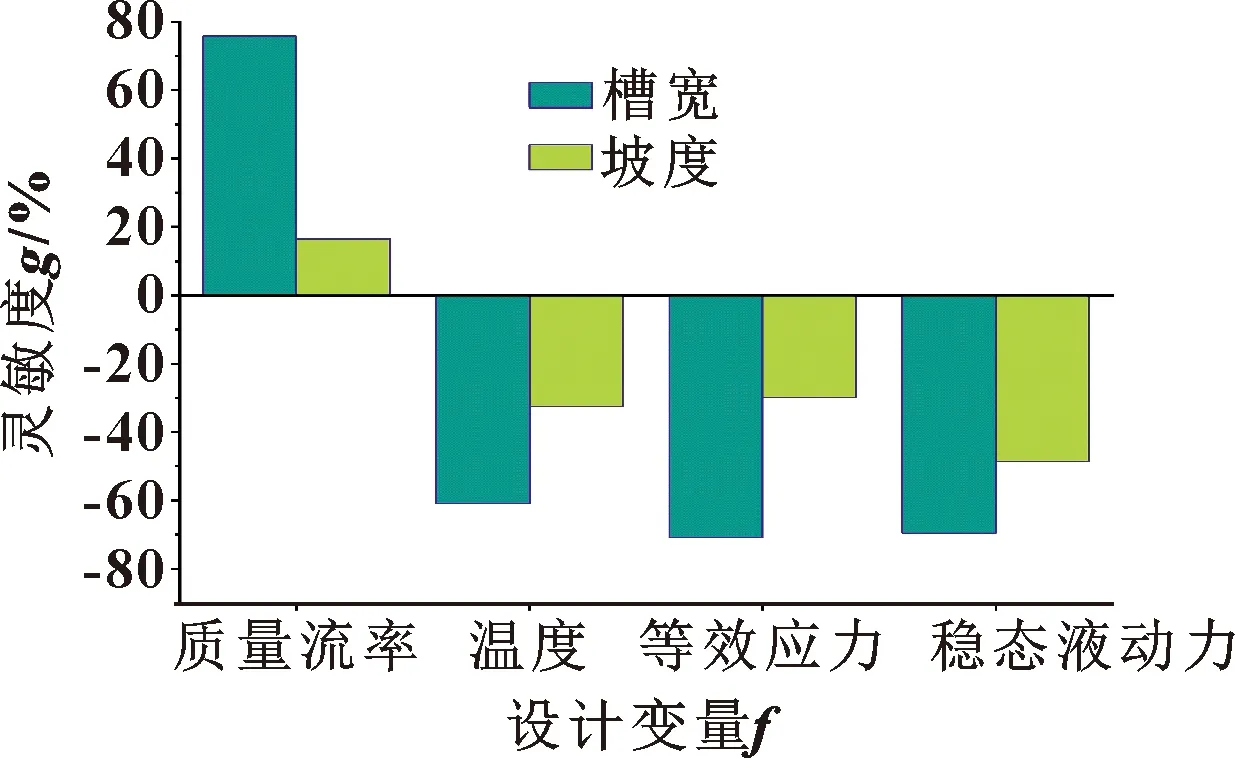
图9 设计变量对目标变量的灵敏度Fig.9 Sensitivity of the design variable to the target variable
4.6 多目标优化
响应面优化设计方法是通过筛选试验设计点来寻找隐式函数的显性多项式方程。对换向阀阀芯节流槽结构进行优化主要是为了减少阀芯开启过程中所受到的液动力,降低阀芯节流槽处所产生的节流损失,提高换向阀换向过程的可靠性及稳定性,同时在满足上述目标的基础上保证阀芯强度及油液温度满足工作要求。因此以液动力及质量流率为目标函数,阀芯等效应力及油液温度为约束条件,建立换向阀阀芯节流槽结构优化设计的数学模型为
varx= [x1,x2]
obj minfF(x)
maxfM(x)
fT(x)<80 ℃
fS(x)<260 MPa
s.t. 0.03≤x1≤0.2
6 mm≤x2≤7 mm
在响应面模型的基础上,经上述灵敏度分析可知,对于不同的响应变量,设计变量对其贡献成不同正负相关性,因此文中采用多目标遗传算法来权衡各响应间的最优解,即Pareto解。该算法基于受控精英概念的流行NSGA-Ⅱ(非支配排序遗传算法Ⅱ)的变体,它支持多个目标和约束,旨在寻求全局最优解。经3 452次评价后收敛,得到最优结构尺寸,如表6所示。
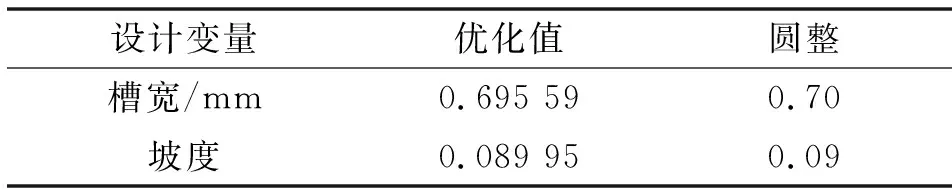
表6 优化结果Tab.6 Optimization results
5 分析对比
将基于响应面结合多目标遗传算法优化所获取的结构参数,通过上述热流固耦合对优化模型进行多物理场耦合求解,与原结构模型对比,分析不同开度下阀芯所受到的稳态液动力,如图10所示。优化后的稳态液动力更加平稳,其峰值液动力也降低了91%,说明该结构能有效地减少阀芯所受到的稳态液动力。
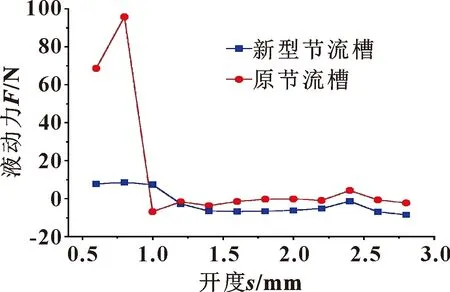
图10 优化前后稳态液动力Fig.10 Steady-state flow force before and after optimization
由图11、12可知:阀芯开度较小时,液体经过节流槽处的速度较大,经过节流槽A1截面后,由于截面面积增大,导致液体流动状态紊乱,出现漩涡。但节流槽A1截面中心由于速度较大,流体在速度方向沿节流槽中心流向阀芯,由伯努利方程可知,该处速度的急剧减少将转换为压力,同时会造成较大的能量损失,转换为热能,使得油温升高。
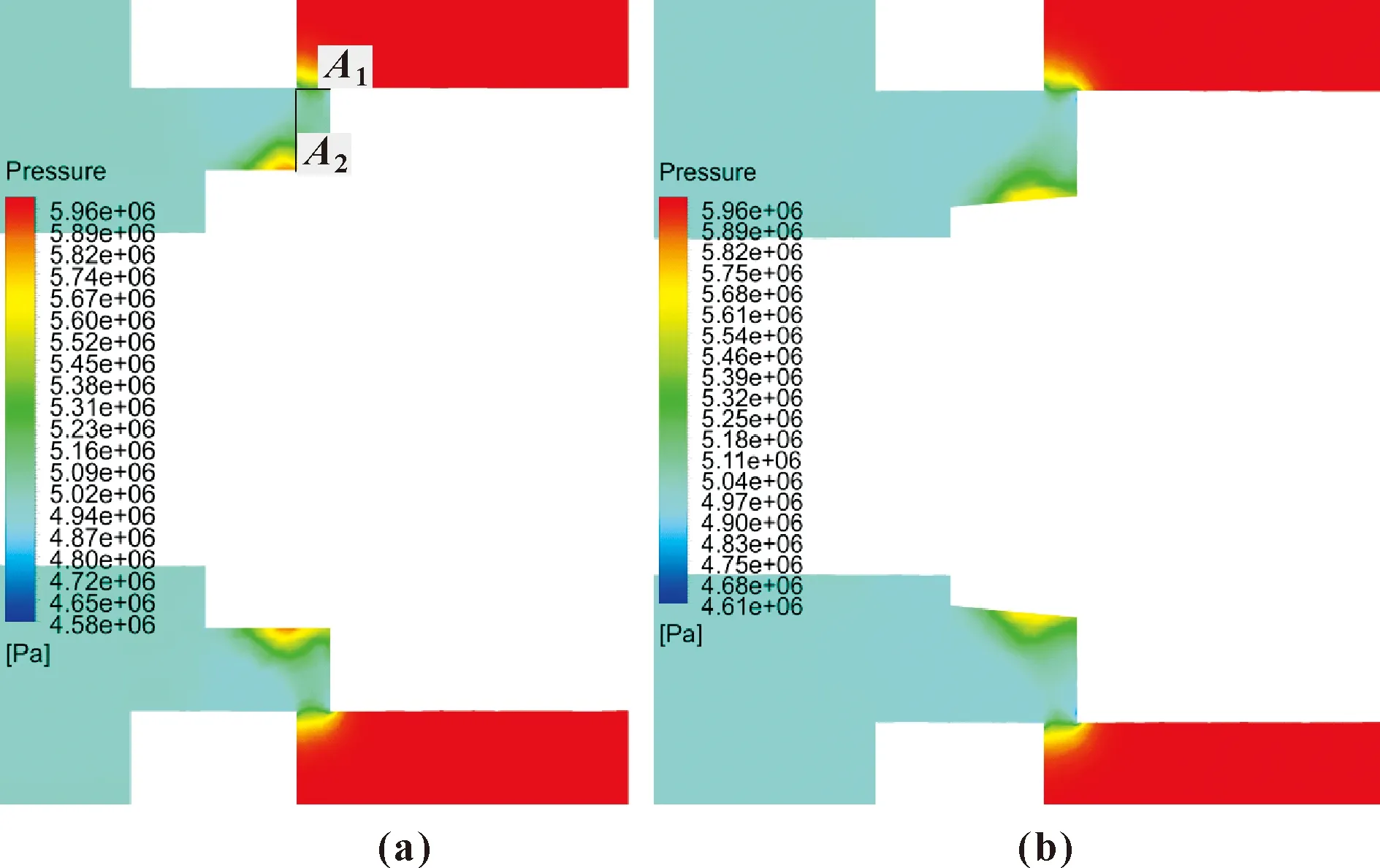
图11 优化前(a)、后(b)压力云图Fig.11 Pressure cloud maps before (a)and after (b) optimization
原结构中由于流体通过节流槽截面A1后直接作用于节流槽水平壁面,造成速度的紊乱,液体在节流槽处来不及稳定而沿水平方向流动。当液体通过节流槽后,液体流通截面进一步扩大,使得液体上下均出现漩涡,如图12(a)所示,进而造成更多的能量损失。而优化后的结构中,液流通过节流槽A1截面后,非水平截面对液体流向有一定的导向性,使得流动更加平缓,由速度矢量图12(b)可知,靠近阀芯壁面处未出现漩涡,进而降低了能量的损失。
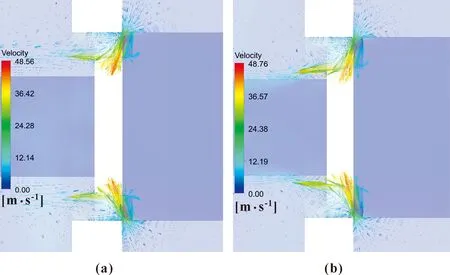
图12 优化前(a)、后(b)速度矢量图Fig.12 Speed vector diagrams before (a)and after (b) optimization
图13所示为开度为0.8 mm下优化前后的三维速度矢量图,显然,图13(b)相较于图13(a)流场分布均匀,流动状态更加有序、平稳。图14所示为优化前后开度为0.8、1.8、2.8 mm下的速度云图,相同开度下的2种结构最大速度基本相同,但优化后模型的流动状态相较于原模型更加稳定。随着开度的增加,其流动状态更紊乱,出口处靠近左壁面的速度与右壁面的速度明显不同。而优化后模型的出口处,随着开度的增加,其平面内的流动速度较为均匀,故其结构优于原结构。
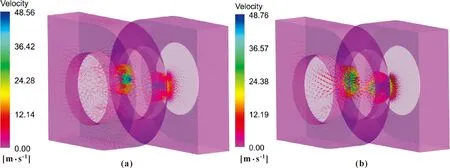
图13 优化前(a)、后(b)三维速度矢量图Fig.13 3D velocity vector diagram before (a)and after (b)optimization
6 结论
针对挖掘机多路换向阀开启过程中受稳态液动力使得操纵力过大导致换向性能差的问题,以降低稳态液动力为主要量化目标,同时为了减少节流槽处所产生的节流损失,以质量流率作为目标函数,基于ANSYS对阀芯节流槽进行热流固多物理场可视化研究,通过分析半圆形节流槽阀芯下的流动状态,提出新型节流槽拓扑结构,建立Non-Parametric Regression响应面模型,研究新型节流槽结构尺寸对稳态液动力与质量流率的影响。结合多目标遗传算法(Multi-Objective Genetic Algorithm,MOGA)对它寻优求解,并对优化前后流动状态及阀芯所受稳态液动力等进行对比分析。结果表明:
(1)优化后的稳态液动力更加平稳,其峰值液动力也降低了91%,新型节流槽结构能够降低稳态液动力,有效提高多路阀开启过程的换向性能。
(2)优化后的结构具有一定的坡度,对液体流向有一定的导向性,使得流动更加平缓,靠近阀芯壁面处未出现漩涡,降低了能量的损失。
(3)随着开度的增加原模型流动状态更紊乱,出口处靠近左壁面的速度与右壁面的明显不同;而优化后模型的出口处,随着开度的增加,其平面内的流动速度大小较为均匀,故其结构优于原结构。
