基于SVMD和自适应MOMEDA的齿轮箱故障诊断
2023-12-04岳子毫裴帮李志远王征兵黄晓丹雷欢欢
岳子毫,裴帮,李志远,王征兵,黄晓丹,雷欢欢
(1.郑州机械研究所有限公司,河南郑州 450001;2.中航光电科技股份有限公司,河南洛阳 471003)
0 前言
随着城市化进程的加深,城市人口大量增加,交通压力越来越大,地铁在不占用地面资源的情况下,大大减轻了道路拥挤。齿轮箱作为地铁列车关键传动零部件,其健康状态会直接影响列车的行驶安全。因此对齿轮箱进行状态检测和故障诊断具有十分重要的现实意义[1]。然而齿轮的振动信号复杂,包括故障信号、轮齿啮合振动信号,同时又受外部噪声与传输路径的影响,故障振动信号往往被噪声淹没。
经验模态分解(Empirical Mode Decomposition,EMD)[2]可以自适应地将任何信号分解为固有模态函数(Intrinsic Mode Function,IMF),EMD在消除白高斯噪声和分数高斯噪声方面取得了巨大成功,然而EMD缺乏严格的数学依据,同时会发生模态混淆[3]。变分模态分解(Variational Mode Decomposition,VMD)由DRAGOMIRETSKIY和 ZOSSO[4]提出。与EMD不同的是,VMD迭代的同时提取IMF。然而,如果信号中可分解模态数量不准确,VMD的性能将会降低。VMD运行时需要正确设置K值[5],高K值可能导致模态混淆或处于纯噪声模态,而低K值可能导致模态重叠。针对选取VMD中K参数,许多学者对此进行了研究[6-8]。在此基础上,NAZARI和SAKHAEI[9]提出了一种称为连续变分模态分解(Successive Variational Mode Decomposition,SVMD)的方法,以连续的方式提取所有IMF,与VMD相比,这种方法无需知道模态的数量并且计算复杂性较低。
盲反卷积法(Blind Deconvolution Method,BDM)作为最经典的方法之一,已经在机械故障诊断领域得到广泛研究并充分应用[10]。反卷积算法本质是寻找最优FIR滤波器,使得观测信号能够还原为原始信号,并最大程度地消除背景噪声的影响。MCDONALD和ZHAO[11]在最小熵反卷积(Minimum Entropy Deconvolution,MED)[12]、最大相关峰度(Maximum Correlated Kurtosis Deconvolution,MCKD)[13]的基础上提出了MOMEDA,相较于MED 和MCKD,MOMEDA不需要采用迭代的方式来寻找最优滤波器参数,可以得到更精确的解。MOMEDA已被广泛地用于旋转机械的故障诊断中,并且取了良好的效果[14-15]。然而MOMEDA需要采用先验知识来确定滤波器长度L和故障周期T,参数的选择会直接影响诊断效果[10]。
综上所述,本文作者提出一种基于SVMD和MOMEDA的齿轮箱故障诊断方法。首先,利用SVMD将故障信号重构;然后,以平均谱负熵为适应函数,通过人工鱼群优化算法(Artificial Fish Swarm Algorithm,AFSA)优化MOMEDA的参数,使得MOMEDA自适应地选择滤波器长度L和故障周期T,并对重构信号MOMEDA滤波;最后,对过滤后的信号进行包络谱分析,提取故障特征。分别在仿真信号和实验数据上进行分析,并与其他方法进行比较,验证所提方法的适用性和可行性。
1 理论背景
1.1 MOMEDA
采集器采集的振动信号表示为
x(n)=g⊗y+e
(1)
式中:⊗为卷积运算;g为系统传输路径的响应;y为故障脉冲序列;e为背景噪声;x为所采集的振动信号。反卷积算法通过寻找最优有限脉冲数字滤波器f,使得观测信号x(t)能够还原为原始信号y(t),并最大程度地消除背景噪声的影响。
多点最优最小熵反卷积以多D-范数为指标,多D-范数及MOMEDA定义如式(2)和式(3)所示。通过多点范数对滤波器参数f=[f1,f2,f2,…,fL]微分求极值,来寻找最佳滤波器参数。
(2)
MOMEDA定义:
(3)
其中:t是一个常数向量,用于标记要反卷积的目标脉冲的位置。
(4)
式(4)中各项
其中:Mk=[xk+L-1,xk+L-1,…,xk]T。
因此等式可以写做:
(5)
通过简化得到
t1M1+t2M2+…+tN-LMN-L=X0t
(6)
令式(6)等于0,得到:
y-1X0t-y-3yX0y=0
(7)
(8)
(9)
如果f是式(8)的解,那么f的倍数也是式(8)的解,所以MOMEDA滤波器的最终表达式为
(10)
1.2 平均谱负熵
旋转机械故障振动信号具有重复瞬变性,表示为冲击性和循环平稳性。ANTONI[16]定义了谱负熵来量化上述2种特性。
在时域中和频域中信号的平方包络谱负熵ΔIε和ΔIE分别为
(11)
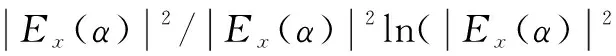
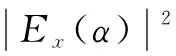
(12)
式中:〈•〉表示均值;εx(n)为信号的平方包络;Ex(α)为信号的平方包络谱。εx(n)和Ex(α)定义分别如式(13)、式(14)所示:

(13)
(14)
式中:j为虚数单位;Fs为采样频率;α为频率。
谱负熵定量反映了能量流动的平稳性,存在冲击的情况下,时域平方包络中能量不再平稳,时域谱负熵增大。在频域中,纯正弦和余弦周期信号在频域平方包络谱体现为冲击成分,所以频域谱负熵表征循环平稳性。综上,可以使用平均谱负熵来综合地反映信号特性。
平均谱负熵表示为
ΔI=ΔIε+ΔIE
(15)
1.3 AFSA优化MOMEDA
在鱼觅食的启发下,李晓磊等[17]提出了人工鱼群多目标优化算法。鱼在觅食时会自主寻找或跟随其他鱼来寻找食物最多的位置,食物最多的位置鱼存活的数量也最多。根据这一特点,人工鱼群算法通过构造多种行为模拟鱼群觅食来实现多目标寻优。
人工鱼群算法优化MOMEDA实现的具体过程如下:
(1)设置寻优范围并初始化优化算法参数;
(2)将鱼群位置初始化,并计算每个个体的初始适应值,记录最优适应值及所处位置;
(3)评价鱼群中每个个体来决定该个体应执行的行为;
(4)执行步骤(3)所选择的行为并更新每个个体位置;
(5)将各个体的适应值与最优值进行对比,以决定是否更新最优值;
(6)当程序达到最大迭代次数时结束,否则跳转到步骤(3)。
该算法流程如图1所示。

图1 人工鱼群算法流程Fig.1 Flow of AFSA
1.4 连续变分模态分解
SVMD本质上是在信号中连续使用变分模态分解(VME),直至提取到所有模态分量或者重构误差小于设定的阈值,同时进行了约束来避免收敛到之前提取到的模态分量。在数学上,假设输入信号f(t)被分解成2个信号:Lth模态分量uL(t)和残余信号fr(t),其表达式为
f(t)=uL(t)+fr(t)
(16)
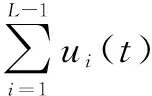
(17)
为了找到第一模态,fr(t)的第一部分为0,SVMD的迭代可以通过式(19)得到:
(18)
(19)
其中:α表示数据保真度约束的平衡参数,可以通过拉格朗日乘数法得到。α的值通常较大。更新ω的方程可以近似表示为
(20)
最后,拉格朗日乘数λ的迭代更新通过双上升法来实现:
(21)
(22)
其中:τ表示更新参数。
SVMD算法逐个提取模态分量,直至重构误差达到阈值,优化问题可以近似地视为每个频率的K维优化问题。
选取2018年1月~2018年7月我军队医院老干部科收治的老年慢性阻塞性肺疾病的患者80例,根据随机分组的方式,将患者分为观察组和参照组,其中有40例患者为参照组,男22例,女18例,年龄58~90岁,平均(73.21±2.17)岁,患病病程1~17年,平均(6.1±2.1)年;而观察组人员也为40例,男23例,女17例,年龄59~89岁,平均(72.39±2.21)岁,患病病程1~17年,平均(6.3±2.2)年,在统计学软件的分析下,两组患者的基本资料比较;差异无统计学意义(P>0.05)。
2 基于SVMD和自适应MOMEDA的故障诊断方法
MOMEDA的故障特征提取效果受参数T和L的影响,选择合适的参数是利用MOMEDA进行故障诊断的关键。利用人工鱼群优化算法,以谱负熵为适应度函数进行多目标优化,选择适应度最大时的滤波器长度和故障周期参数,实现参数的自适应选择,避免人工选择导致诊断效果不佳。但是在强噪声背景下,MOMEDA不再具有免疫性,文中利用SVMD作为前处理对原始信号进行降噪,减弱噪声的影响。
综上,提出了结合SVMD和自适应MOMEDA的故障诊断方法,具体流程如下:
(1)合理设置SVMD平衡参数、双提升时间步长、收敛准则容差、停止准则类型等参数,通过SVMD分解故障信号得到IMF分量,利用所有IMF分量之和进行重构;
(2)合理设置ASFA的参数,包括滤波器长度和周期的寻优范围、种群大小、步长、人工鱼的视野、重复次数、迭代次数等,利用ASFA算法自适应选择最优滤波器参数;
(3)利用优化算法所得的滤波器参数,对步骤(2)得到的重构信号进行MOMEDA;
(4)对步骤(3)得到的信号进行包络分析,判断故障类型。
3 仿真信号验证
为验证所提方法的有效性,文中采用ADAMS模拟仿真地铁齿轮箱小齿轮断齿,所得到的数据进行故障特征提取与诊断。采用加速度传感器采集振动信号,测点位置为输入端轴向方向,故障类型为小齿轮断齿。齿轮箱和小齿轮轴模型及测点位置如图2所示。仿真齿轮箱为单级减速齿轮箱,具体参数如表1所示。实验过程中,采样频率为10 000 Hz,所采样点数为5 001。

表1 齿轮箱参数(仿真)Tab.1 Gearbox parameters(simulation)
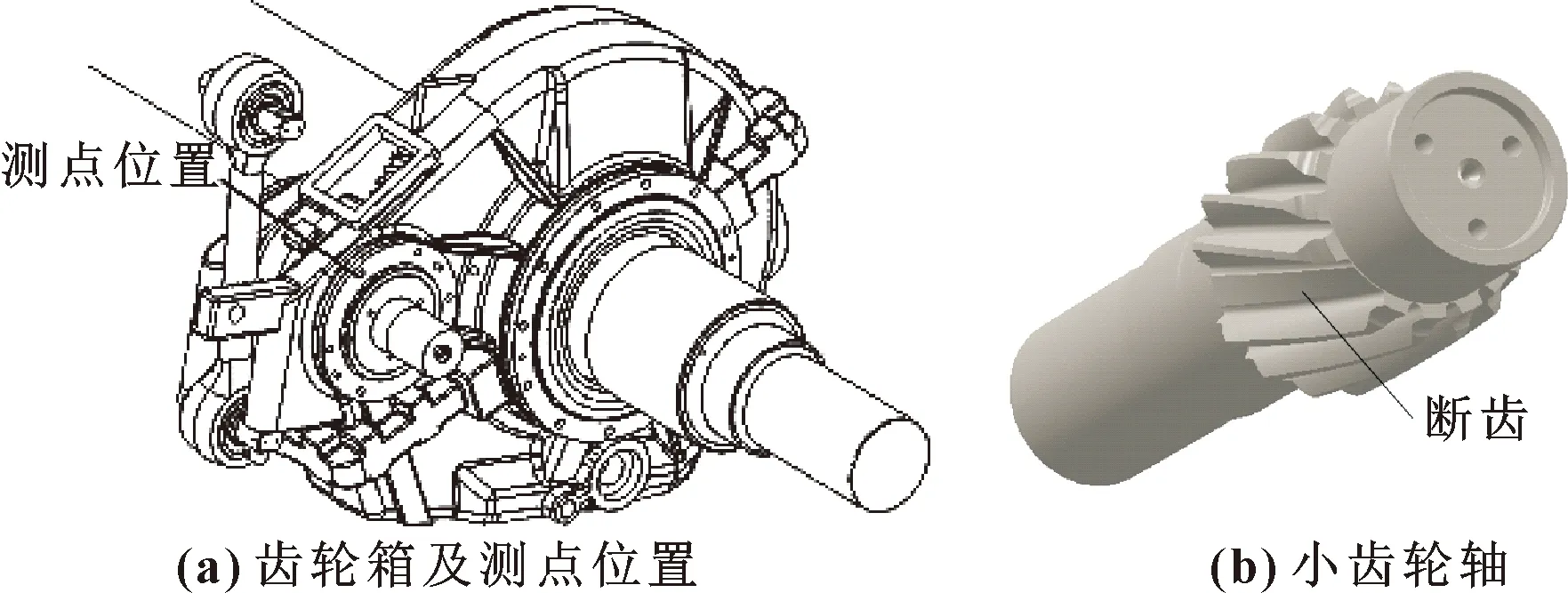
图2 齿轮箱三维模型Fig.2 Gearbox 3D model:(a)gear box and measuring point position;(b)pinion shaft
测得振动信号如图3所示。受噪声的影响,原始时域信号很难辨别出周期性脉冲成分。利用SVMD,将故障特征与噪声信号分离。设置最大余额参数α=2 000,双上升步长为0,收敛准则的容差为1×10-6,停止标准为收敛到最后一个模态分量的能量,经过SVMD分解获得7个IMF分量成分,前5个分量如图3所示。对每个分量求和得到重构信号如图4所示。可以看出:重构信号相对于原始信号减弱了部分噪声,对重构信号进行包络谱分析,包络频谱图如图5所示。

图3 原始时域信号(仿真)Fig.3 Original time domain signal(simulation)
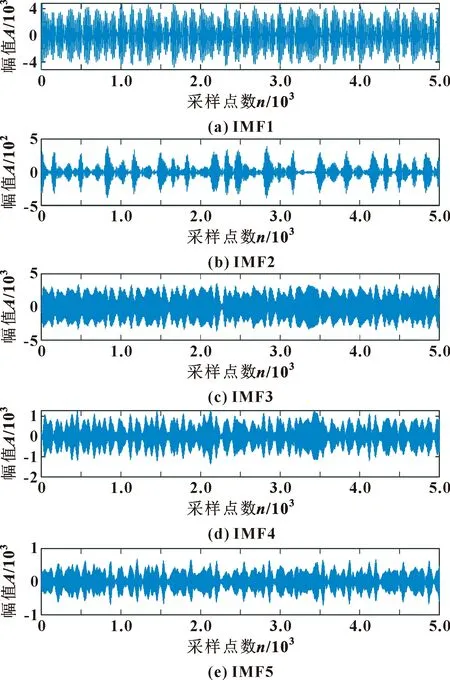
图4 SVMD获得的前5个IMF分量(仿真)Fig.4 The top five IMF components obtained by SVMD (simulation):(a)IMF1;(b)IMF2; (c)IMF3;(d)IMF4;(e)IMF5
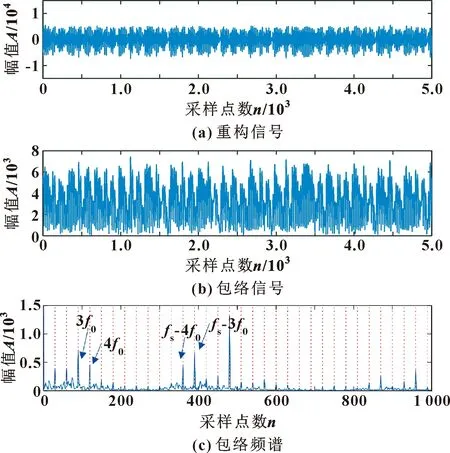
图5 重构信号及其包络分析(仿真)Fig.5 Reconstructed signal and its envelope analysis (simulation):(a)reconstructed signal;(b) envelope signal;(c)envelope spectrum
包络频谱中可以初步看出故障频率及啮合频率,但是故障频率只在3f0、4f0及啮合频率边频带fs-3f0、fs-4f0幅值较为明显,其他倍频处幅值较小,故障特征不明显,容易受到噪声的干扰。因此,重构信号之后,通过MOMEDA对故障信号进一步去噪。
在MOMEDA滤波处理之前,利用人工鱼群算法多目标寻优来寻找最优滤波器长度L和故障周期T。设置ASFA算法迭代次数为20,鱼群数量为30,寻优区间为[500,1 000]和[350,500],最多试探次数为100,感知距离为1,拥挤度因子为0.618,步长为1。参数寻优曲线如图6所示,多目标寻优后得到L和T分别为528.570和333.582。利用得到的最优参数对重构信号进行MOMEDA降噪,得到的输出信号及其包络频谱如图7所示。
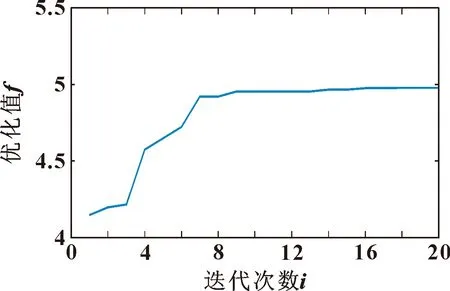
图6 人工鱼群优化算法的迭代过程(仿真)Fig.6 Iterative process of AFSA(simulation)
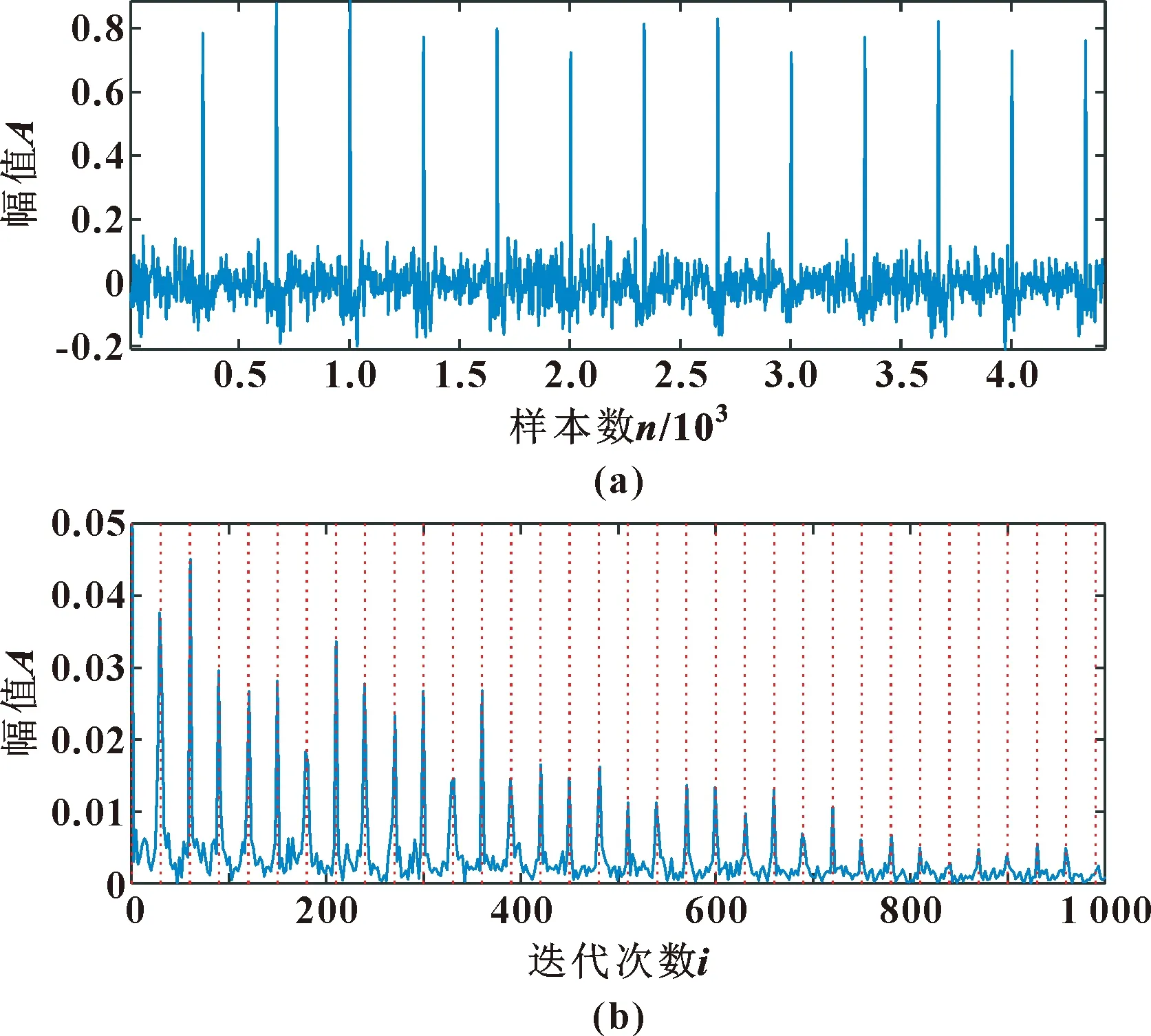
图7 MOMEDA滤波后的时域信号(a)和包络频谱(b)Fig.7 The time domain signal (a)and envelope spectrum (b)after MOMEDA filtering
将该方法与MCKD进行比较来验证所提方法的优越性。设置滤波器长度为500,故障周期为330,迭代次数为30,经过MCKD滤波后时域图如图8(a)所示。对滤波后信号进行包络谱分析,包络频谱如图8(b)所示。
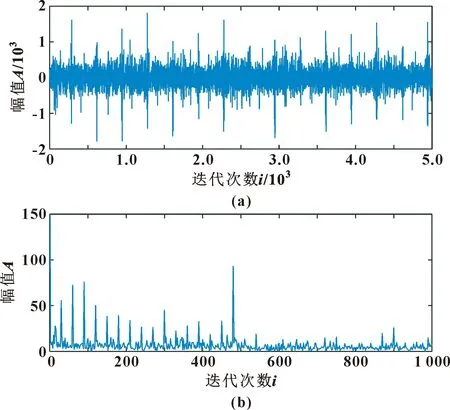
图8 MCKD滤波后的时域信号(a)和包络频谱(b) (仿真)Fig.8 Time domain signal (a)and envelope spectrum(b) after MCKD filtering(simulation)
通过2种方法的对比可以明显看出:文中提出的方法更优。采用所提方法得到的时域信号可以清楚地分辨出周期性脉冲。同时在包络频谱中,故障频率及其倍频处的幅值更加明显。由此可见,文中提出的结合SVMD和自适应MOMEDA在齿轮箱故障检测具有良好的可行性和适用性。
4 实验验证
为进一步验证所提方法的有效性,利用实验现场采集的振动信号进行验证。实验信号来源于地铁齿轮箱,其具体参数如表2所示。齿轮箱及测点位置如图9(a)所示。齿轮箱的故障类型为断齿,采用线切割的方式将轮齿从齿根处切除,如图9(b)所示。实验现场如图9(c)所示。

表2 齿轮箱参数(实验)Tab.2 Gearbox parameters(experimental)

图9 实验条件Fig.9 Test conditions:(a)gear box and measuring point position;(b)pinion shaft;(c)test site
传感器采用加速度传感器,采样频率为10 240 Hz,所采集的振动信号时域波形如图10所示。设置SVMD最大余额参数α=1 200,双上升步长为0,收敛准则的容差为1×10-6,停止标准为收敛到最后一个模态分量的能量,经过SVMD分解得到15个IMF分量,前5个分量如图11所示。通过对每个分量求和得到重构信号如图12所示。
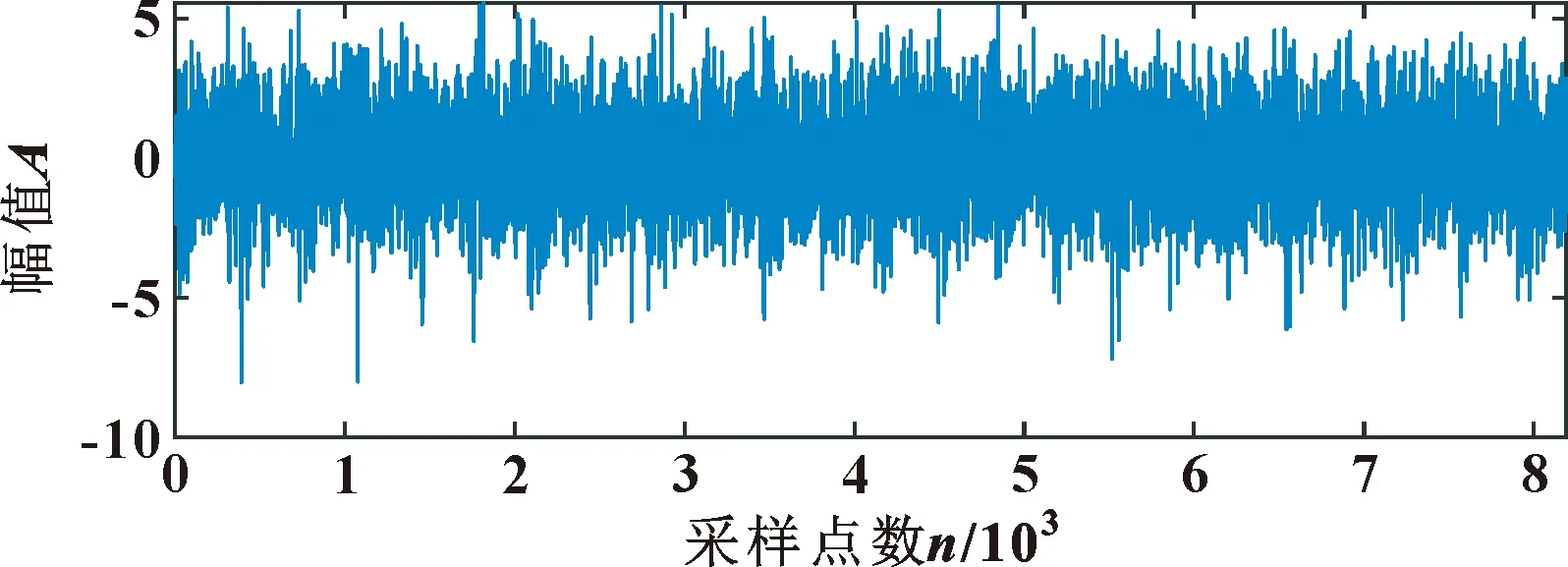
图10 原始信号(实验)Fig.10 The original signal(experimental)
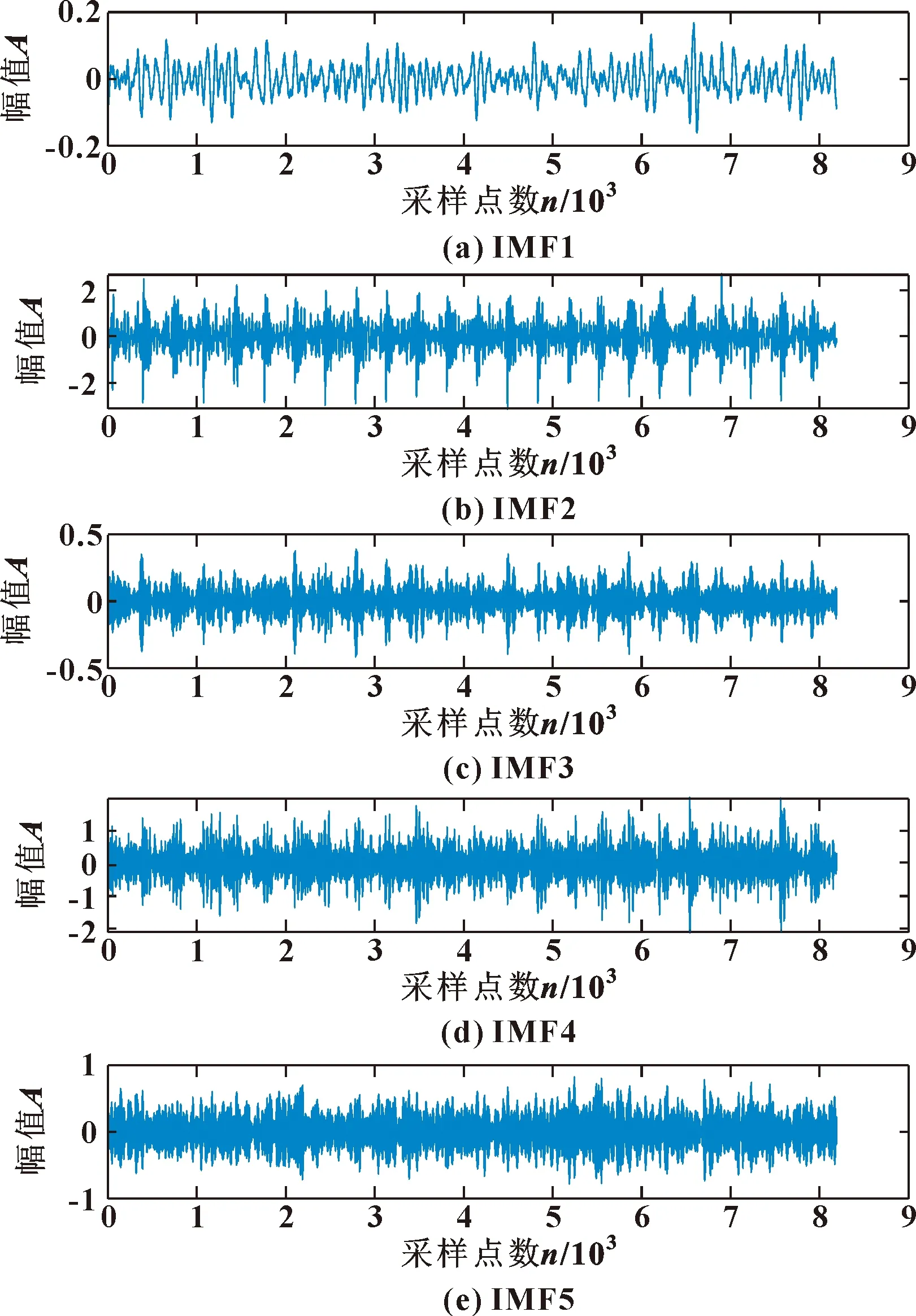
图11 SVMD获得的前5个IMF分量(实验)Fig.11 The top five IMF components obtained by the SVMD (experimental):(a)IMF1;(b)IMF2; (c)IMF3;(d)IMF4;(e)IMF5
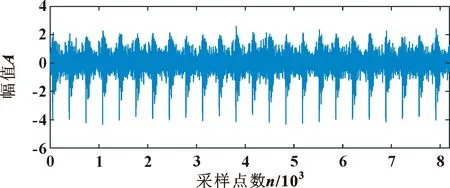
图12 SVMD获得的重构信号(实验)Fig.12 Reconstructed signal obtained by SVMD (experimental)
利用人工鱼群算法自适应选择滤波器长度L和故障周期T,设置鱼群数量为40,迭代次数为20,L和T的寻优区间分别为[500,1 000]和[250,450],经过优化得到最优参数L和T分别为573.476 1和341.942 2。人工鱼群算法迭代过程如图13所示。将MOMEDA参数设置为上述所得到的最优参数,重构信号经过MOMEDA滤波后得到时域波形、包络信号和包络频谱如图14所示。

图13 人工鱼群算法的迭代过程(实验)Fig.13 Iterative process of AFSA(experimental)
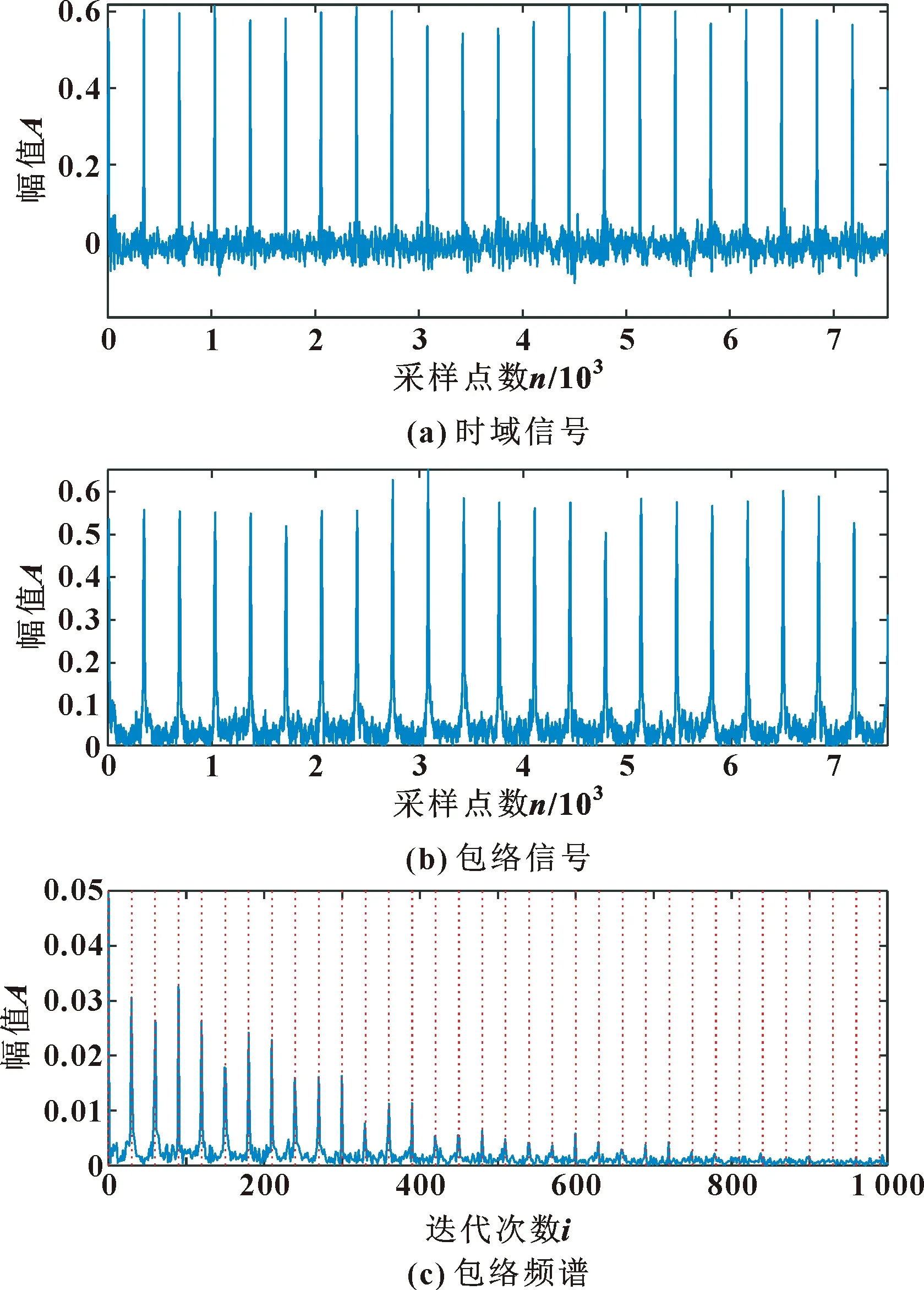
图14 MOMEDA滤波后的时域信号及其包络分析(实验)Fig.14 The MOMEDA filtered time domain signal and its envelope analysis(experimental):(a)time domain signal; (b)envelope signal;(c)envelope spectrum
所提方法得到的信号的周期性脉冲特性在时域图中突出,从包络频谱中提取的故障特征频率及其倍频分量的峰值明显。以上结果进一步证明了所提方法在工程实践中的有效性和适用性。
为了进一步验证所提方法的优越性,将它与其他方法进行比较。基于MCKD方法获得的时域信号及其包络频谱如图15所示。
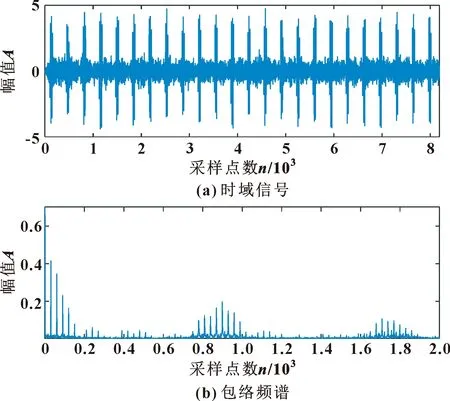
图15 实验信号的MCKD分析Fig.15 MCKD analysis of experimental signals:(a)time domain signal;(b)envelope spectrum
从图15(a)中虽然可以看出周期性脉冲,但是存在明显的噪声干扰。观察包络频谱,故障频率集中在低倍频和啮合频率的调制频率,幅值较小,故障频谱较所提方法较不突出。通过与MCKD对比验证了该方法的优越性。
5 结束语
针对强噪声背景下故障提取效果欠佳,提出了基于SVMD和自适应MOMEDA的齿轮箱故障诊断方法,经过分析得出以下结论:
(1)SVMD作为前处理降噪可以减弱噪声的干扰,同时相比较VMD不需要知道信号中可用模态的数量,计算复杂度较低,可以成功收敛到真实模态分量。
(2)使用平均谱负熵作为适应函数,应用人工鱼群算法对MOMEDA参数寻优,实现了自适应选择参数,避免人工选择的误差,参数的最优选择提高了MOMEDA故障特征提取性能。
(3)分别在仿真信号和实验信号上进行了验证,所提方法准确地识别出故障特征,并与其他方法进行了比较,验证了所提方法的有效性和适用性。
