新型四自由度并联隔振系统的机构设计与分析
2023-12-04李亚晶岳义韦宝琛崔国华刘国兴
李亚晶,岳义,2 ,韦宝琛,2 ,崔国华 ,刘国兴
(1.上海工程技术大学机械与汽车工程学院,上海 201620;2.上海交通大学机械与动力工程学院,上海 200240)
0 前言
救护车在行驶过程中会因路面不平而引起上下振动,因制动与启动引起前后振动,因转弯引起左右振动,即在x、y、z3个方向上振动[1]。这些振动通过车身传递到病人所在的担架上,伤员会受到来自垂直、纵向、横向的振动冲击,不仅不能有效地保护伤员,还会对伤员造成二次伤害。研究表明:大约10%的伤员会在运输的过程中出现病情恶化的现象[2]。针对此类问题,国内外研究机构和学者通过设计不同减振装置解决。
并联机构因具有承载高、刚度好、精度高、动态特性好等优点[3]而被广泛应用于各个领域。如运动模拟器(飞行模拟器、娱乐模拟系统、汽车运行模拟器)、微操作机器人(医疗设备、微加工、生物工程)、航天对接器、并联机床等。同样,并联机构在减振装置中也有很大的应用,吸引了大批学者进行研究。如KARNOPP等[4]设计并研究了有关航空航天器的整星隔振系统;WANG等[5]提出了一种新型的微隔振Stewart平台;朱伟等人[6]构建了以3-PUU并联机构为主体结构的三平移减振平台;杨启志等[7]设计一种新型三自由度汽车并联减振座椅;牛军川、张福亮[8]针对3-PRC机构的不足,设计一种3-PRRP4R并联机构,用来解决多维振动问题;罗敏等人[9]设计了一种“并联隔振装置”承载隔振一体化系统用来保证成像质量。
其中救护车减振装置因对重症伤员的保护作用而被重点研究。通过将担架安装在减振装置上实现对不期望振动的降低或抑制,来削减救护车行驶过程中对病人造成的二次伤害。早在1990年张铁砚、刘军[10]就对轻型救护车减振担架进行设计研究;同年黄永勇[11]对两自由度减振担架模型进行了平顺性分析。近年来,SHINTANI等[12]提出了救护车病床二维基础隔离装置;徐新喜等[13]提出了采用小刚度弹簧并附加液压阻尼器的阻尼减振方案用于救护车担架;李骏等人[14]利用 MATLAB/Simulink建立九自由度救护车—担架—卧位人体振动系统仿真模型,有效提高人体舒适度;高翔等人[15]对4-PUU并联机构进行改进,有效隔离了沿坐标轴的平移振动以及绕X轴的旋转振动;徐鸿佳等[16]基于3-RPS并联机构对越野救护车车载平衡装置进行分析,得出该机构在Z轴方向上的移动和绕X、Y轴的转动有良好的输出效果,在一定空间内具有较高的灵巧度,且奇异性非常低。上述研究虽然在多维减振方面有了一定成果,但并没有考虑实际救护车尺寸以及装置的安装空间,导致目前救护车减振装置不能应用在实际场景中。
为了隔离所有方向上的旋转和移动,需要一种六自由度的隔振装置。但在救护车设计过程中,考虑到需要在拥堵路段快速通过,对车身的宽度进行了压缩,同时,车内需要医护人员陪同,车内空间进一步降低,这使得减振装置的尺寸要求严格。五自由度以及六自由度的装置安装空间存在着较大的问题。二自由度以及三自由度不能很好地改善担架的振动影响,所以为了在有限空间内能尽可能地补偿更多维度的振动,四自由度的并联机构是一种较好的解决方法。空间四自由度是少自由度并联机构中重要分支,已有不少学者对此进行了研究。马履中等[17]基于船舶仪器设备的减振要求,提出具有冗余四自由度的并联机构作为减振装置;刘旭升等[18]提出一种四自由度广义球面并联机构来满足踝关节康复运动需求;彭红梅等[19]针对自动化生产线分拣需求,提出一种新型四自由度的三平移一转动(3T1R)并联机器人机构;卢月红、徐彩莲[20]提出一种可实现三平移一转动的空间并联机器人机构,并利用方位特征集理论分析机构的自由度和方位特征集;HAN等[21]提出一种用于高速场合的3T1R四自由度并联机器人。目前,许多学者仍将空间四自由度机构的研究重心放在3T1R或者3R1T上面,2T2R的研究还相对缺乏。虽然2T2R四自由度并联机构的运动效果更佳,但因为无法避免奇异位型的出现,这类机构的研究相对较少。
综上所述,针对救护车在运载重症伤员时因启动、制动、转弯与颠簸使车身发生垂直、前后、横滚与俯仰4个自由度方向的振动问题,本文作者基于螺旋理论提出一种具有两移两转(2T2R)运动特性的新型的2RRU-2UPS四自由度并联隔振装置。通过全雅克比对其奇异性进行分析,不改变其运动特性的条件下,在2个RRU支链上分别增加RPU支链构成混合支链用以避免奇异或者避免接近奇异,最终提出2-UPS-2-(RP-RR)U对称并联隔振装置。基于螺旋理论对其连续转轴进行分析,确定该机构的2条连续转轴,验证该机构运动的连续性。通过分析其结构特征,运用闭环矢量法建立运动学逆解模型,运用MATLAB软件进行编程,验证其运动模型的正确性,同时结合边界搜索法仿真出该机构的工作空间,为设计者提供理论基础。
1 四自由度隔振装置机构设计
1.1 机构设计方法
在螺旋理论中,力螺旋与运动螺旋的互易积为零时互为反螺旋。并联机构设计的核心是寻找运动支链,为平台提供相应的运动与约束。对设计n个自由度的非冗余并联机构来说,必须要满足以下几个条件:(1)运动平台至少有n个自由度;(2)每一个支链的自由度个数必须大于等于n;(3)所有的支链自由度共同作用之后其和一定等于n;(4)每个分支的约束螺旋个数必须小于等于(6-n);(5)所有支链的约束螺旋共同作用之后,整个系统的约束螺旋一定为(6-n)。并联机构动平台的约束可以表示为
(1)
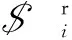
设计一款每个分支都相互对称并且每个分支上所受到的约束也相同的机构十分困难。但如果单独考虑并联系统的所有分支,考虑4个特殊的子系统分布类型,设计过程将会被简化。对于n自由度非冗余并联机构,根据其约束的类型可分为两大类:一类是分支机构中有6个运动螺旋没有约束集;另一类是运动螺旋不足6个有约束集。如式(2)所示:
(2)
1.2 四自由度并联机构设计
救护车的振动主要是由道路颠簸引起的垂直振动和救护车启动与制动引起的前后振动,即在Z轴与X轴方向上的移动。同时为了保证患者的舒适度,救护车的倾斜也需要平衡,即在X轴以及Y轴上的转动。所设计的救护车隔振装置至少需要4个自由度运动,即X&Z平移自由度和X&Y旋转自由度,如图1所示。
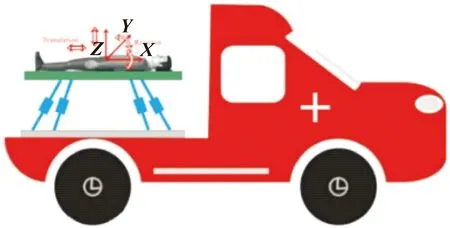
图1 隔振装置的运动分析Fig.1 Motion analysis of vibration isolation device
根据螺旋理论当中的运动螺旋以及约束螺旋的关系,可以得到四自由度2R2T(2-旋转-2-平移)移动平台的运动螺旋系统。移动平台的2个转动2个移动运动螺旋(2-ξ0-2-ξ∞) 如图2(a)所示,相应的约束螺旋如图2(b)所示,包含了沿Y轴方向的力约束以及沿Z轴方向的力矩约束。ξ0、ξ∞、ζ0和ζ∞分别代表着转动、移动、约束力和约束力矩。
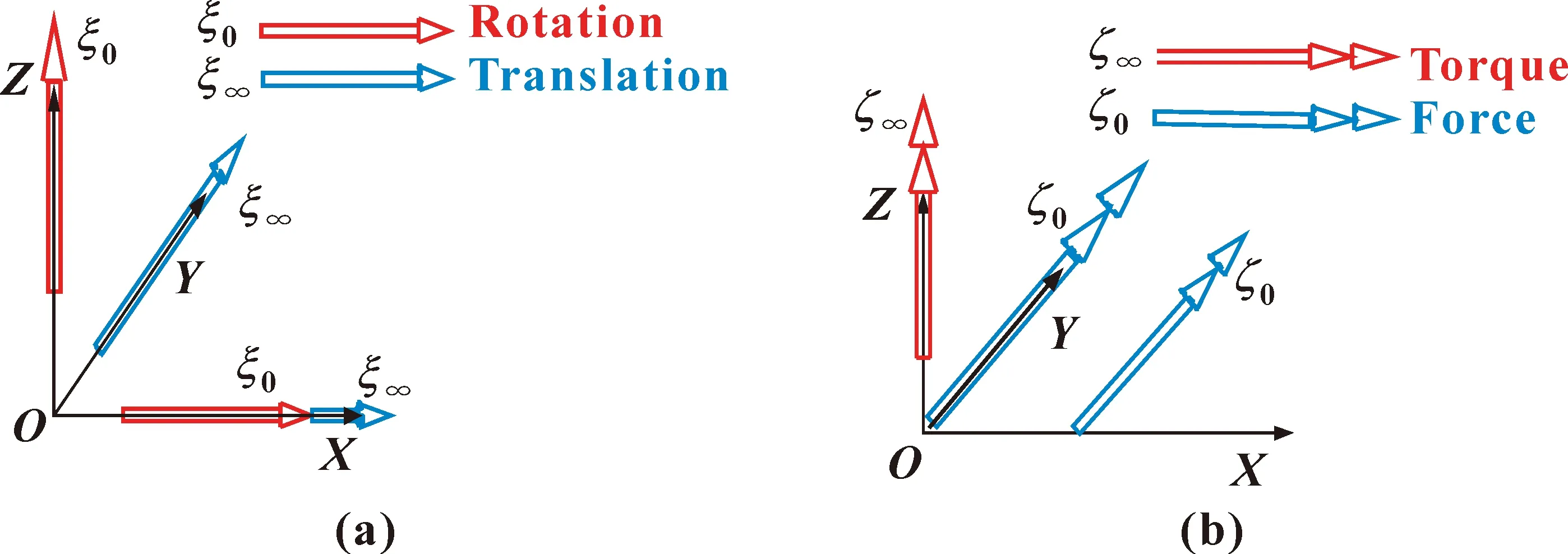
图2 2R2T并联机构的运动螺旋(a)和约束螺旋(b)Fig.2 Motion screw (a)and constraint screw (b)of 2R2T parallel mechanism
许多分支系统所呈现的运动是等效的,如一个约束力与一个约束力偶共同作用与两个约束力共同作用所产生的约束是等价的。第一个约束螺旋系是由一个沿Y方向的约束力以及一个沿Z轴方向的约束力偶组成的。第二个是由沿Y轴方向的两个约束力组成的,同时这两个约束力所组成的平面要垂直于Z轴。
并联机构分支中的约束螺旋包括1-ξ0、1-ξ∞、1-ξ0-1-ξ∞或者是没有运动螺旋。根据螺旋理论当中约束螺旋与运动螺旋的关系,即当约束力与该分支所有转动副轴线共面且与所有移动副轴线相互垂直时,两者互为反螺旋;当约束力偶与该分支所有转动副轴线相互垂直时,两者互为反螺旋。
如图3所示:只有一个约束力的支链应满足:(1)所有的转动副轴线都应平行于约束力;(2)所有的移动副都应垂直于约束力。如图4所示,只有一个约束力偶的支链应满足所有的转动副垂直于约束力偶。如图5所示,一个约束力与一个约束力偶共同作用的分支链应满足:(1)所有的转动副轴线都应平行于约束力;(2)所有的转动副都应垂直于约束力偶;(3)所有的移动副都应垂直于约束力。
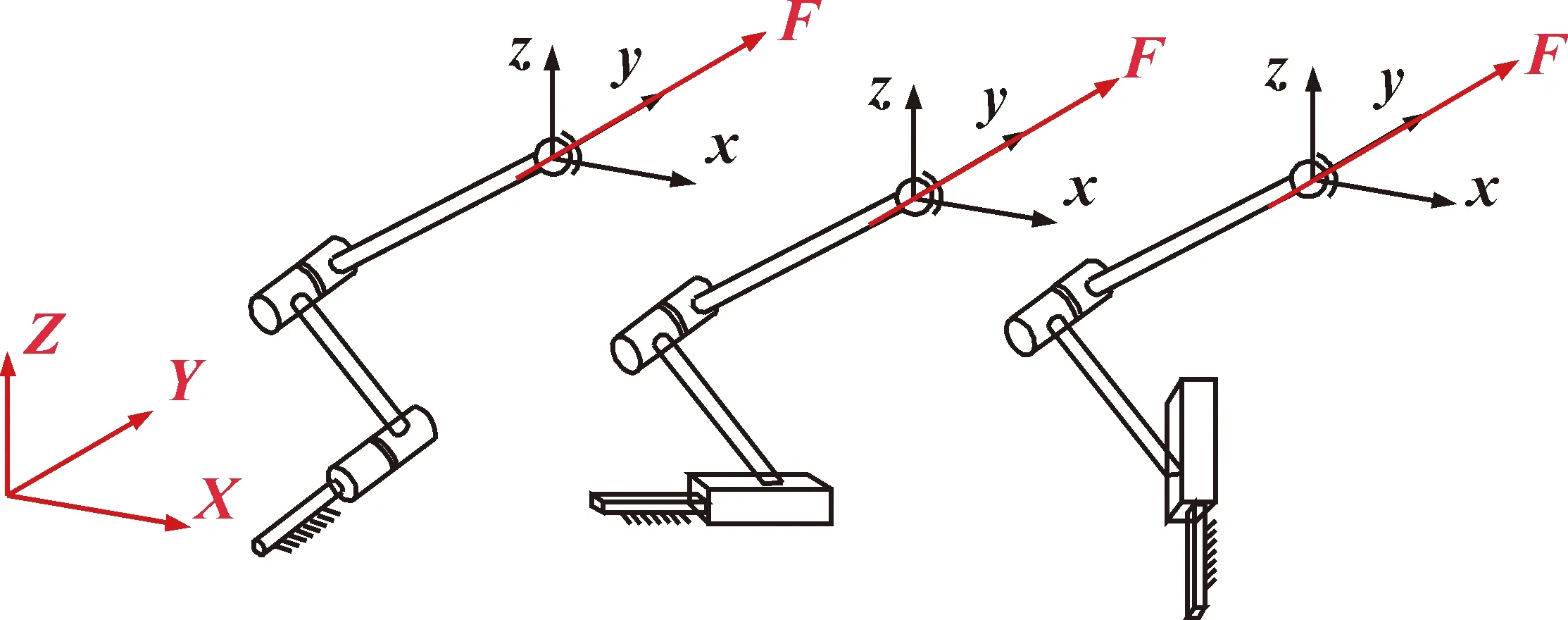
图3 带有一个约束力的分支Fig.3 Branch with a force constraint
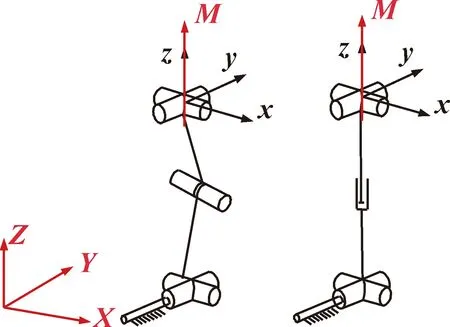
图4 带有一个约束力偶的分支Fig.4 Branch with a torque constraint
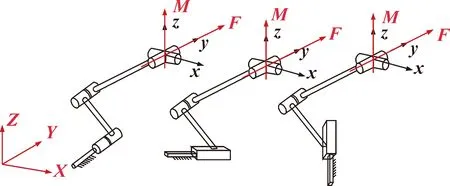
图5 带有一个约束力和一个约束力偶的分支Fig.5 Branch with a force constraint and a torque constraint
通过公式(2)对并联机构分支类型进行选取。令公式(2)中的m=2,使得4个分支中的2个分支提供所有的约束,另外2个分支不提供约束。带有约束螺旋的分支可以从1-ξ0、1-ξ∞、1-ξ0-1-ξ∞这3种分支中选择,这些分支的约束螺旋共同作用后为1-ξ0-1-ξ∞或 2-ξ0的约束系。2R2T并联机构中的其他2个不带约束螺旋的分支可以选择UPS链。2R2T并联机构简图如图6所示。
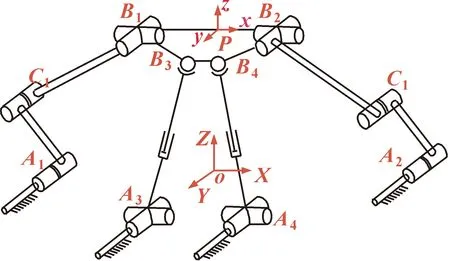
图6 2RRU-2UPS机构简图Fig.6 2RRU-2UPS mechanism diagram
2 全雅可比矩阵奇异分析
2RRU-2UPS的结构简图如图6所示。2个UPS支链中的移动副作为其驱动副(轴线位于AiBi之上),2个RRU支链中与机架相连的2个转动副作为其驱动副(轴线位于Ai沿Y轴方向向上)。静平台(A1A2A3A4)位于静坐标系O-XYZ当中,其原点位于A1A2中心处,动平台(B1B2B3B4)位于动坐标系P-xyz当中,其原点位于B1B2中心处。
一个球关节相当于3个相交的非共面转动关节,一个万向节相当于2个相交的转动关节。移动平台的瞬时螺旋$p表达式如下:
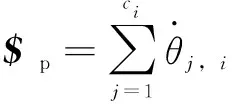
(3)
式中:θj,i定义为速度;$j,i定义为第i条支链的第j个关节的单位螺旋;ci定义为每条支链的自由度个数;移动平台的运动螺旋定义为$p=[ωTvT]T,其中ω是移动平台的角速度,v是运动平台中一点的线速度,它与表示螺旋的参考系的原点瞬间重合。
该机构的全雅可比[22]为
(4)
(5)
其中:bi=PBi;mi=BiCi;sj,i为第i条支链第j个关节的轴线方向。
Jc为该机构的约束雅可比,由支链所提供的约束螺旋构成,其表达式为
(6)
其中:ni为垂直于万向铰平面的单位约束力偶。
机构将会在以下几种情况下发生奇异:(1)4个驱动约束力共面即动平台与静平台重合;(2)4个驱动约束力在空间相交于一点;(3)2条RRU支链不在同一平面且不完全对称;(4)4个驱动约束力两两相交的交点所形成的转轴与动平台Y轴平行。
机构不仅在奇异点处无法正常运行,同时其性能在奇异点的周边空间极差。为避免机构奇异或接近奇异,并在有限空间内保证该机构具有高刚度、抗偏载能力强、运动响应快等性能,在2个RRU支链上分别增加RPU支链构成一个混合链,万向铰作为共用U副,如图7所示;4个移动副作为机构的驱动副,其结构简图如图8所示;三维模型如图9所示。
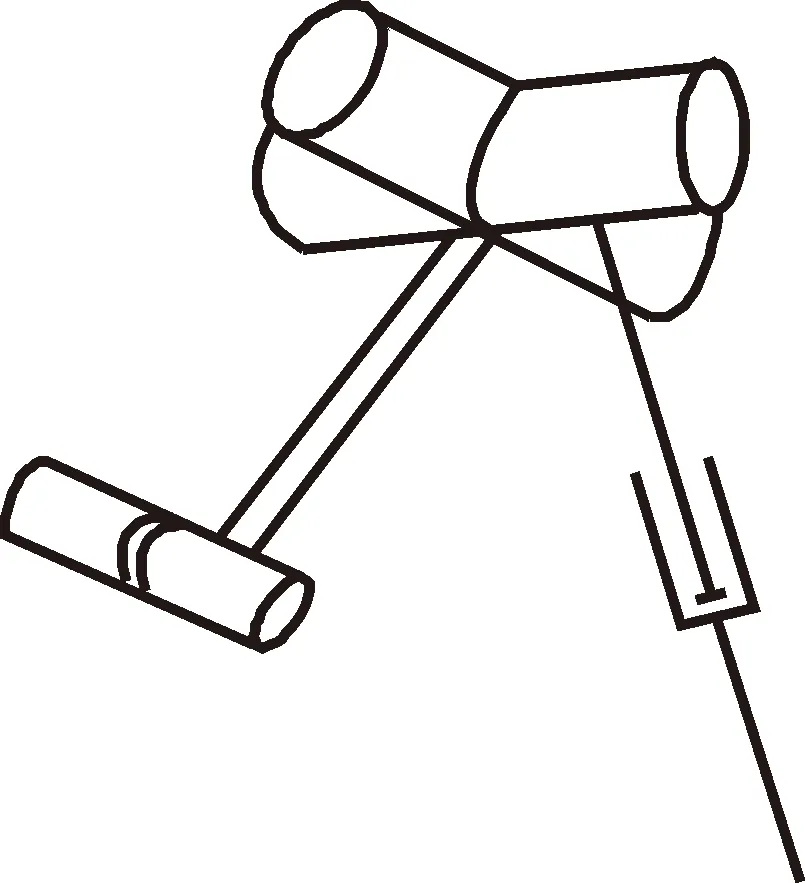
图7 混合支链局部示意Fig.7 Partial schematic of mixed branching chain
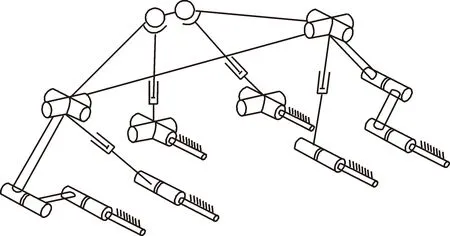
图8 机构简图Fig.8 Mechanism diagram
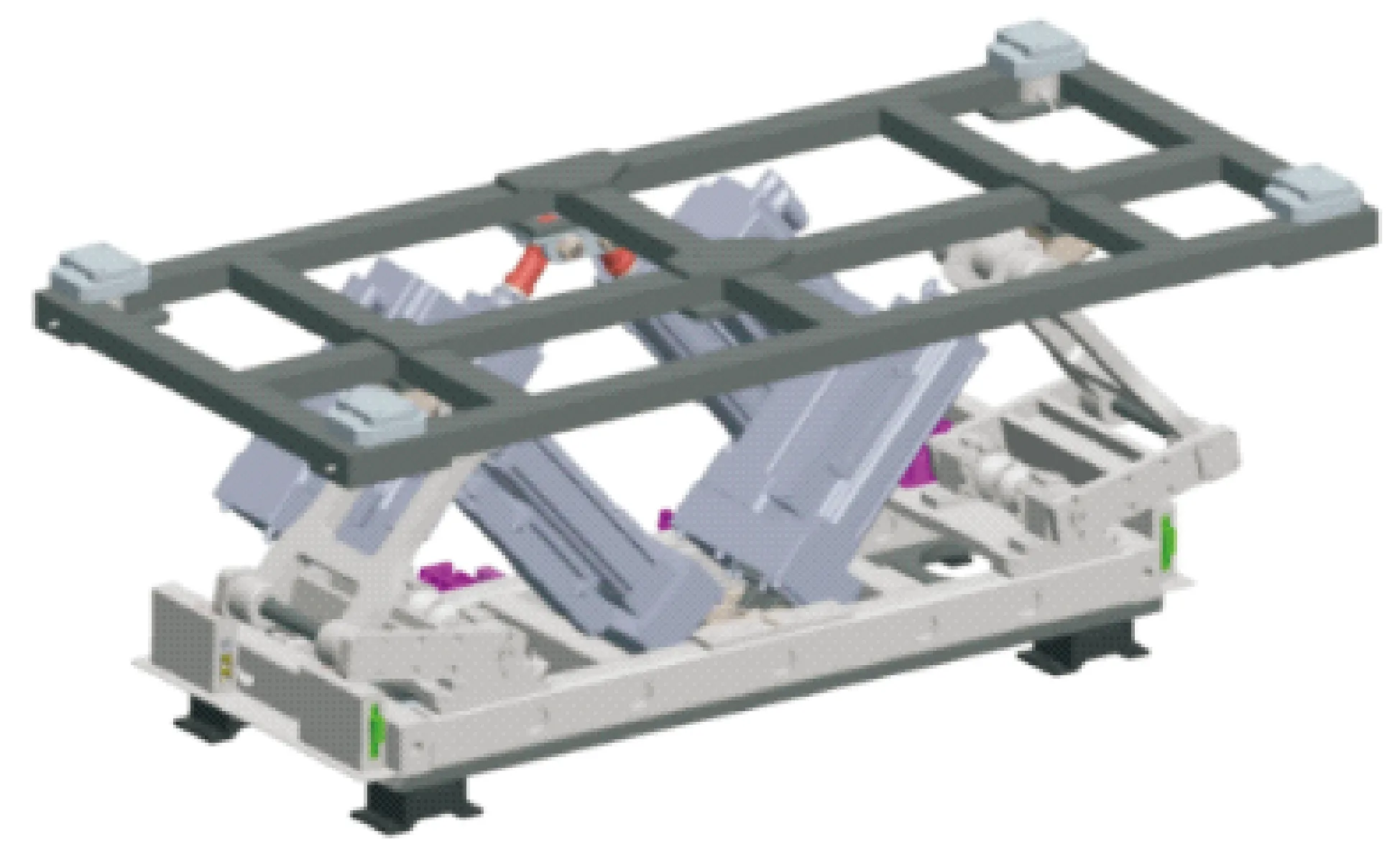
图9 机构三维模型Fig.9 Mechanism 3D model
3 运动转轴的连续性
3.1 自由度分析
基于螺旋理论对机构进行自由度分析,将移动副看作是节距为无穷大的偶量,将转动副看作是节距为零的线矢量,使用修正的G-K公式对该机构进行自由度求解:
(7)
其中:d为机构的阶;n为机构中包括机架总的活动构件的数目;g为运动副的数目;fi为第i个运动副的自由度数目;v为机构的过约束;ξ为机构的局部自由度。
式中,N为脉冲波形的总的采样点,m为饱和点数,a为线性系数,c为修正偏移量.通过窗宽自适应形心修正算法对原始数据进行预处理滤波,并根据不同饱和度波形的饱和点获得适应本波形的窗宽,进而以调整后的窗宽滑窗取样,获得窗宽W的数据x=[xa xa+1…xa+W]和y=[ya ya+1…ya+W],对获得的波形数据求加权和并与前一次比较,在滑窗过程中获得形心计算的起始位置xt
M=6×(14-16-1)+24+2-4=4
通过修正的G-K公式可以得到该机构的自由度为4,符合预先设定的动平台自由度要求。
3.2 初始位形下连续转轴分析
在初始位形下,在动平台建立动坐标系P-xyz,在静平台建立静坐标系O-XYZ。点Ai在静坐标系中的坐标为(XAi,YAi,0),点Bi的坐标为(XBi,YBi,ZBi)。机构位形如图10所示。
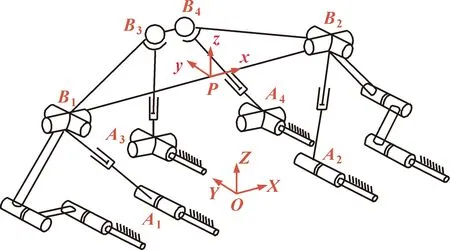
图10 初始位形简图Fig.10 Initial configuration diagram
该机构的约束螺旋[23]为
(8)
4个分支对动平台施加的2个约束螺旋构成平台的约束螺旋系,对其求反螺旋可得:
(9)
3.3 绕B1B2杆连续转动后的转轴分析
机构绕B1B2杆连续转动后的机构位形如图11所示。
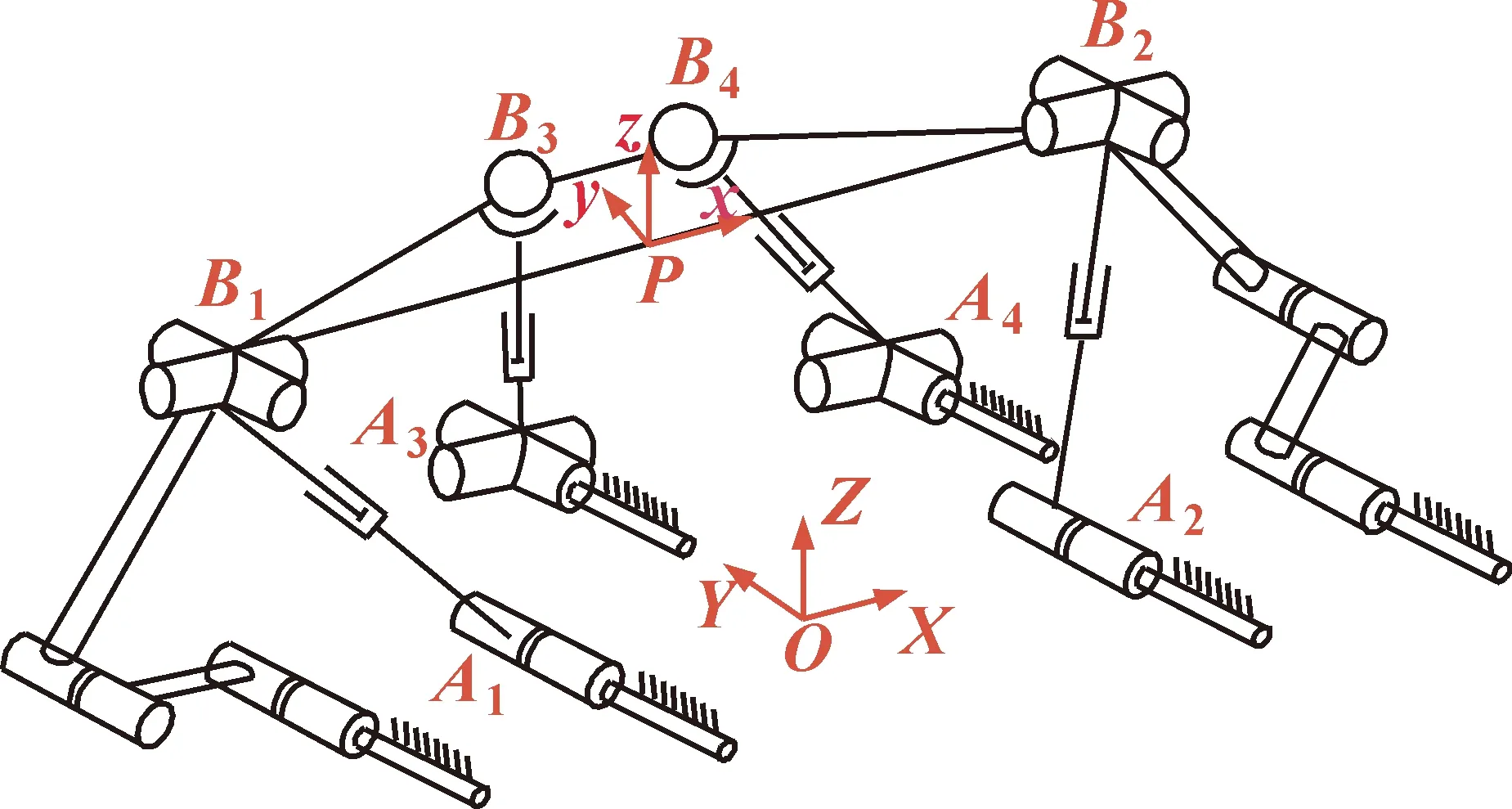
图11 绕B1B2杆连续转动后的机构简图Fig.11 Mechanism diagram after continuous rotation around the B1B2 rod
转动后的机构约束螺旋为
(10)
4个分支对动平台施加的2个约束螺旋构成平台的约束螺旋系,对其求反螺旋可得
(11)
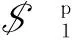
3.4 先绕Y轴再绕B1B2连续转动后的转轴分析
复合转动后机构位形如图12所示。
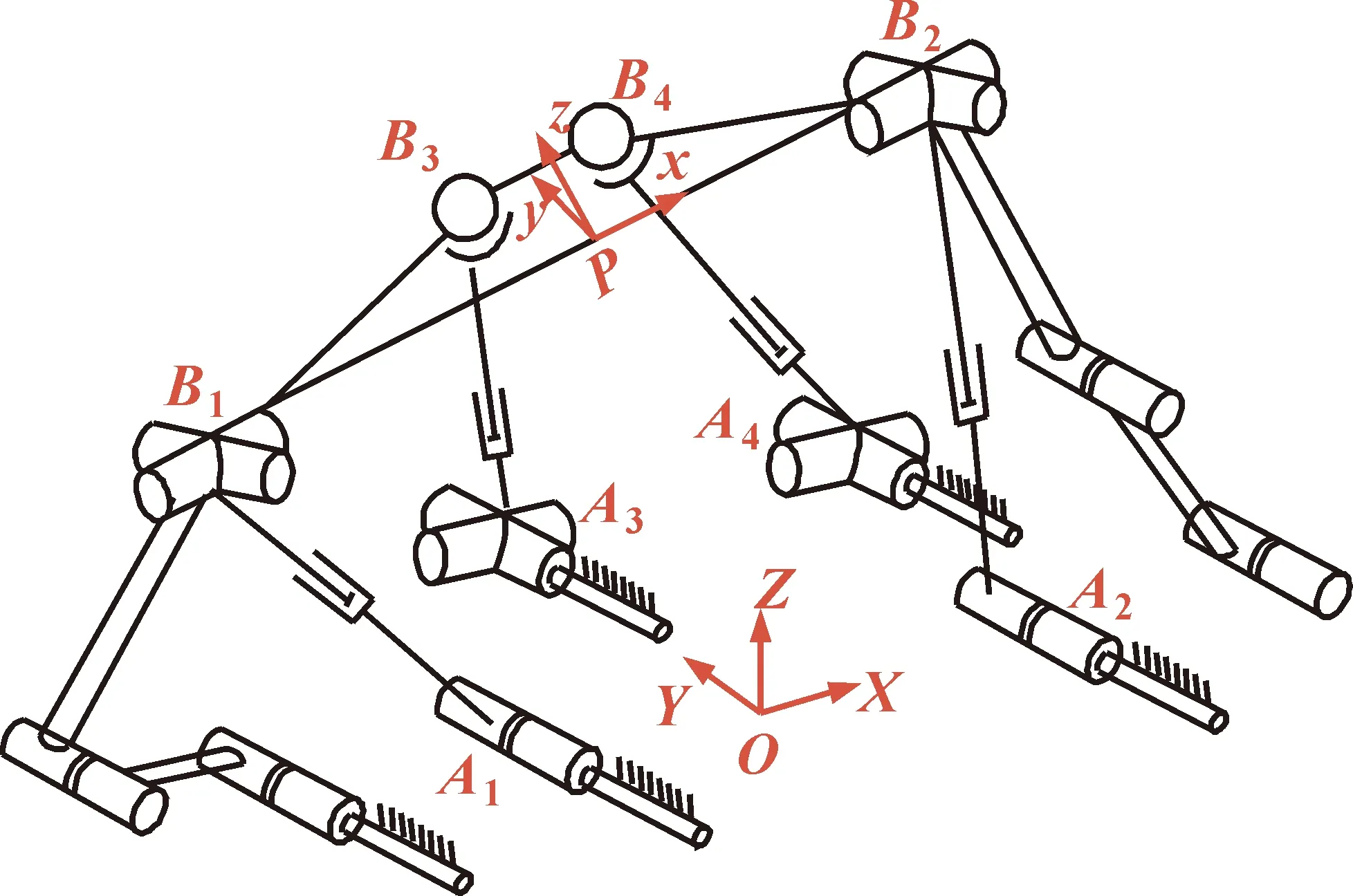
图12 两次转动后的机构简图Fig.12 Mechanism diagram after two rotations
转动后该机构的约束螺旋为
(12)
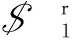
4个分支对动平台施加的2个约束螺旋构成平台的约束螺旋系,对其再次求反螺旋可得:
(13)
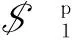
综上所述,在动平台连续转动后仍可以绕B1B2杆与静坐标系Y轴转动,即B1B2杆与Y轴为该机构的2个连续转轴。其中静坐标系中的Y轴是该机构的固定转轴,不随动平台的变化而变化,B1B2杆为任意转轴,随着动平台的变化而变化。
4 运动学反解模型
求解2-UPS-2-(RP-RR)U并联机构的运动学位置反解,即给定机构的尺寸参数、动平台末端点x和z方向上的坐标以及动平台的姿态(θx,θy),求4个驱动副的位移qi(i=1,2,3,4)。如图10所示,在动平台建立动坐标系P-xyz,在静平台建立静坐标系O-XYZ。定义p为动坐标系原点相对于静坐标系原点的位置矢量;定义ai为在静坐标系下点Ai的位置矢量;定义bi为在动坐标系下点Bi的位置矢量;定义li为各个支链在静坐标系中的位置矢量。
在该并联机构中,θx、θy、θz分别为绕x、y、z轴的转动角度,因为该机构没有在z方向上的转动,即θz=0,则动坐标系相对于静坐标系的姿态可以表示为
R=Ryx(θy,θx)=Ry(θy)Rx(θx)
(14)
根据该机构的几何特性可以得到以下的闭环方程:
p+Rbi=ai+li…(i=1,2,3,4)
(15)
解得支链在静坐标系中的位置矢量li为
li=p+Rbi-ai…(i=1,2,3,4)
(16)
设机构位于初始位置时各个支链的长度为Li(i=1,2,3,4),可以得到各个支链的驱动输入qi(i=1,2,3,4),如下所示:
(17)
若已知该机构末端在静坐标系中的广义位姿信息,可以通过上式求出各个支链的驱动输入。上述公式为系统的运动学反解模型。
5 工作空间
机器人的工作空间是衡量机器人性能的重要指标。文中所述的2-UPS-2-(RP-RR)U对称并联隔振机构能实现在XOZ平面的二维移动以及绕X轴与Y轴的转动。
现给定该机构的基本尺寸参数如表1所示。
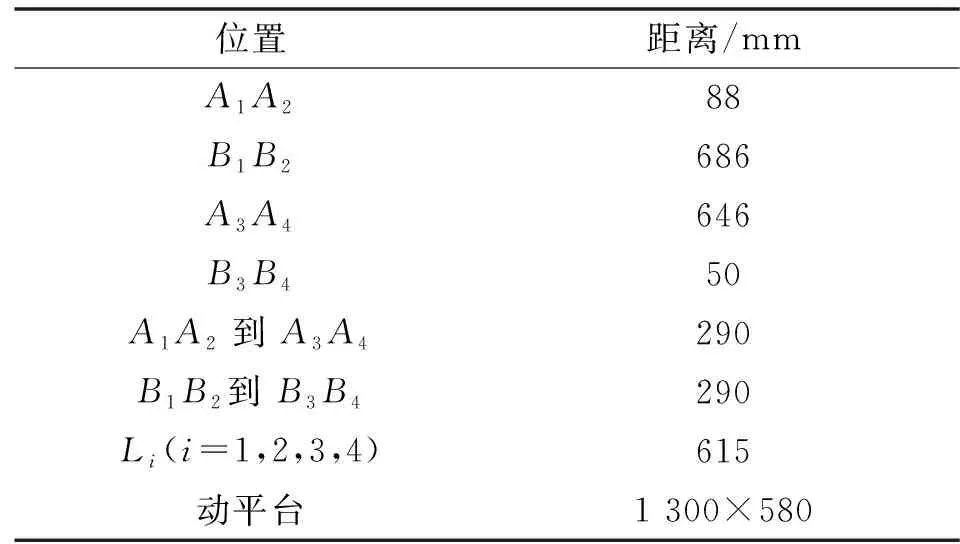
表1 参数尺寸Tab.1 Parameter size
在运动模型的基础上,以运动反解算法为原型,结合边界搜索法在MATLAB仿真软件中编写工作空间算法,给定杆长范围(450~730 mm)并通过随机选取未知参数来获得参考点p可达到的所有点,即2-UPS-2-(RP-RR)U并联机构的工作空间。仿真结果如图13所示。
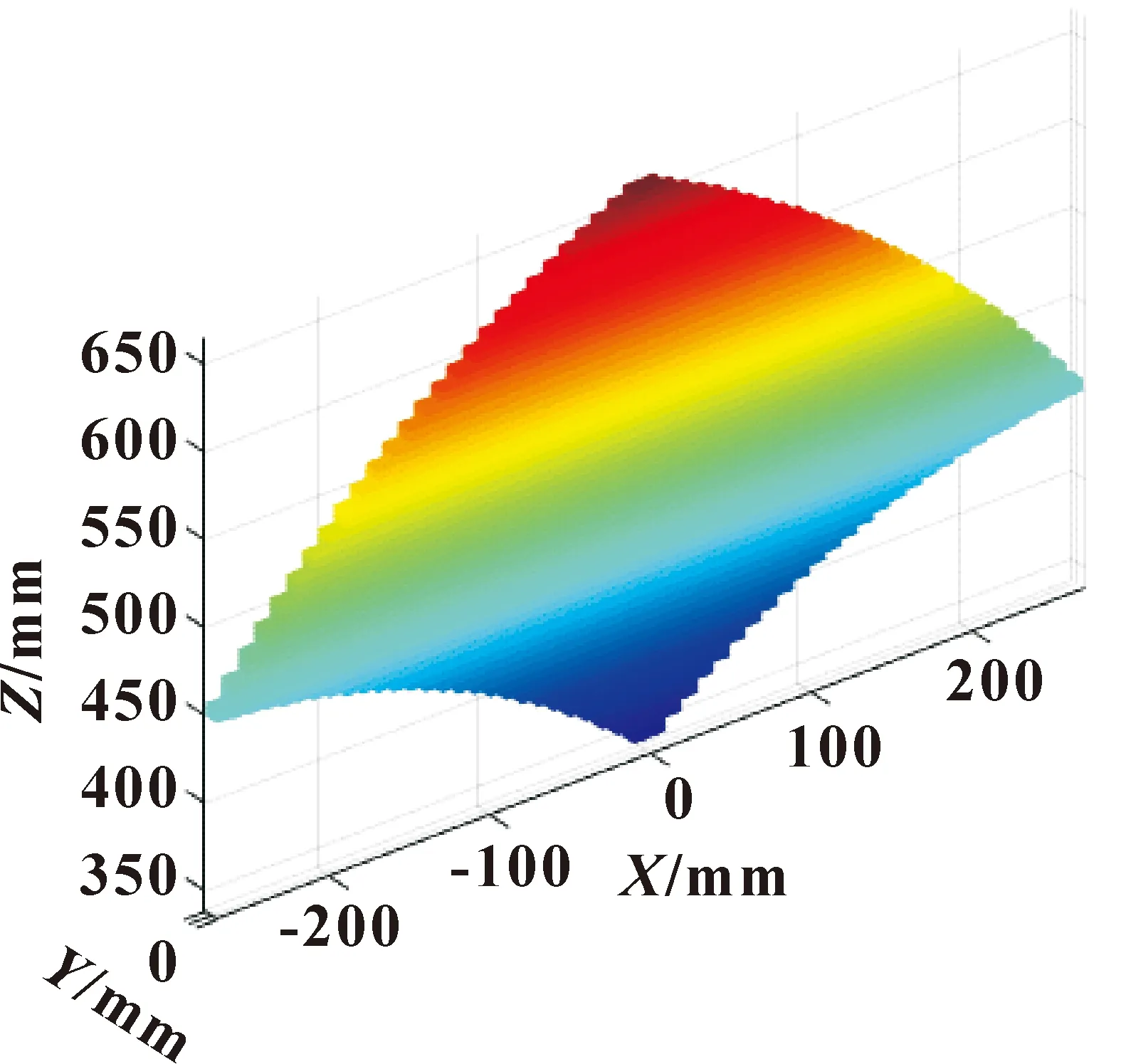
图13 工作空间Fig.13 Workspace
由图13可知:该新型2-UPS-2-(RP-RR)U对称并联隔振机构的工作空间关于X=0对称。结合该机构采用关于YOZ平面完全对称布置这一结构特点,该工作空间符合机构的理论分析与实际运动状况。
6 结论
(1)提出了一种新型的2-UPS-2-(RP-RR)U对称并联隔振装置,该机构具有2个转动自由度和2个移动自由度,具有承载能力高、动态特性好等优点。
(2)通过全雅可比矩阵对其奇异性进行分析,采用2-(RP-RR)U混合支链代替2-RRU支链,在不改变其运动特性的情况下避免了奇异位形的出现。
(3)确定了该机构的两条连续转轴,分别为过静坐标系原点且沿Y轴方向的固定转轴与过动平台两U副中心点的任意转轴,验证了该机构运动的连续性。
(4)采用封闭矢量法建立了运动学逆解模型,结合边界搜索法在MATLAB中仿真出的工作空间,验证了运动学模型的正确性。
