张拉整体机器人构型设计及非线性力学特性分析
2023-12-04刘瑞伟林勋涛郭宏伟王春龙谢浩唐振宇
刘瑞伟,林勋涛,郭宏伟,王春龙,谢浩,唐振宇
(1.广州航海学院船舶与海洋工程学院,广东广州 510725;2.哈尔滨工业大学机器人技术与系统国家重点实验室,黑龙江哈尔滨 150001)
0 前言
近年来,随着科技的发展,深空探测已成为航空航天领域的重要研究方向[1-2]。在深空探测任务中,传统探测机器人存在造价贵、着陆方式复杂、投放数量少等问题[3-5],因此,新型星球探测器的研制愈发迫切。
张拉整体结构是由杆、索间的自应力实现稳定的空间网格结构,其设计特点是刚体悬挂在弹性元件的平衡张力网络中。作为一种新兴类型的软机器人,在外载的作用下,它表现出柔顺、轻巧、抗冲击的特性,因其可进行折叠存储、实现批量投放以及完成深空探测、深海探测、灾后救援等危险且未知性极高的任务,近年来成为各国桥梁建筑、航空航天、机器人等领域的研究热点[6-10]。
目前对于张拉整体结构的研究主要集中在找形及形状优化上,其中力密度法[11]、动力松弛法[12]、能量法[13]和迭代算法[14]等被广泛应用。清华大学ZHANG 等[15]提出了一种新型力密度法并成功应用于张拉整体结构的找形研究中,提高了找形效率。哈尔滨工业大学LU等[16]基于动态松弛法研究了张拉整体结构力学特性,并提出多组实例进行验证。东南大学CAI等[17-18]基于力密度和分组方法,提出了一种针对多应力模态张拉整体的找形方法,通过最小化能量函数获得张拉整体结构的节点和拉索的空间位置。西安电子科技大学林敏等人[19]针对传统力密度法找形效率低下的问题,采用改进鱼群算法与力密度法相结合,提高了张拉整体结构找形效率。哈尔滨工程大学罗阿妮等[20]基于力平衡原理,依据构件与节点连接矩阵定义,完成自应力稳定构型及分析。
与找形相比,张拉整体概念在工程实践中的应用很少。典型的张拉整体结构工程应用有YOU和 PELLEGRINO[21]提出的可展开天线DMR,哈尔滨工业大学刘荣强教授团队研制的张拉整体式天线结构[9,22],NASA提出的“SUPERball”六杆张拉整体机器人[23-24]及加州伯克利分校研制出“TT-X”系列张拉整体机器人[25-26]。
在深空探测工作中,张拉整体机器人将被直接从太空投放至星球表面,着陆时会受到很大的冲击力。为防止因载荷过大而出现压杆屈曲失效、拉索屈服失效等问题,从而导致探测任务失败,研究载荷状态下结构力学特性十分必要。CAI等[27]基于典型的张拉整体结构模型,研究了考虑初始缺陷的张拉整体结构力学行为。TRAN和LEE[28]提出了一种用于张拉整体结构弹性分析中大变形的数值方法,考虑了几何和材料的非线性。
因此,本文作者针对六杆张拉整体结构,通过节点矩阵和连接矩阵,建立张拉整体结构的数学模型。在此基础上,结合ANSYS软件,建立六杆张拉整体结构的非线性力学分析模型,进行六杆张拉整体结构的力学性能分析和结构参数的敏感度分析,得出提高六杆张拉整体结构力学性能的有效方法;最后研制六杆张拉整体机器人样机进行翻滚实验,验证六杆张拉整体机器人的运动性能。
1 六杆张拉整体机器人构型设计
图1所示为美国航空局AMES研究中心提出的六杆张拉整体机器人进行地外行星探测的任务示意。
在MATLAB环境中,通过建立节点矩阵、连接矩阵及矢量矩阵,构建了一种六杆张拉整体结构数学模型,为后续力学性能分析提供基础。
1.1 节点矩阵
因此,可以得到任一节点坐标,坐标通式可以表示为
(1)
式中:ni(i=1,2,3,…,12)表示第i个节点的坐标;Xi、Yi、Zi表示第i节点的坐标。
因此,六杆张拉整体结构的节点矩阵可以表示为
(2)
1.2 构件连接矩阵
在张拉整体结构的数学模型中,通过构建连接矩阵可以反映各个构件和节点之间的函数关系。六杆张拉整体结构每个节点上连接1根杆构件和4根索构件,在连接矩阵中,构件起点对应元素为“-1”,构件终点对应元素为“1”。杆构件及其连接节点具体连接情况如表1所示。

表1 杆构件与节点的连接Tab.1 Connection relationship between bars and nodes
根据杆单元及其连接节点的情况,可以推导出杆构件的连接矩阵为
(3)
同理,可以通过相同的方法获得索构件及其两端节点的连接矩阵:
(4)
1.3 构件矢量矩阵
利用节点矩阵和连接矩阵可以获得相应构件向量。所有杆构件组成结构的杆构件矢量矩阵,其表达形式为
(5)
式中:bi(i=1,2,…,6)表示第i根杆向量。
同理,所有索构件组成结构的索构件矢量矩阵表达形式为
(6)
式中:si(i=1,2,…,24)表示第i根索向量。
设原点为直线n1n2中点O,n1、n2和n5为着地点,并作为全约束节点。通过上述分析,即可在MATLAB软件中计算六杆张拉整体结构节点坐标矩阵、连接矩阵及构件矢量矩阵,建立六杆张拉整体结构的数学模型,如图2所示,为后续力学性能分析提供基础。
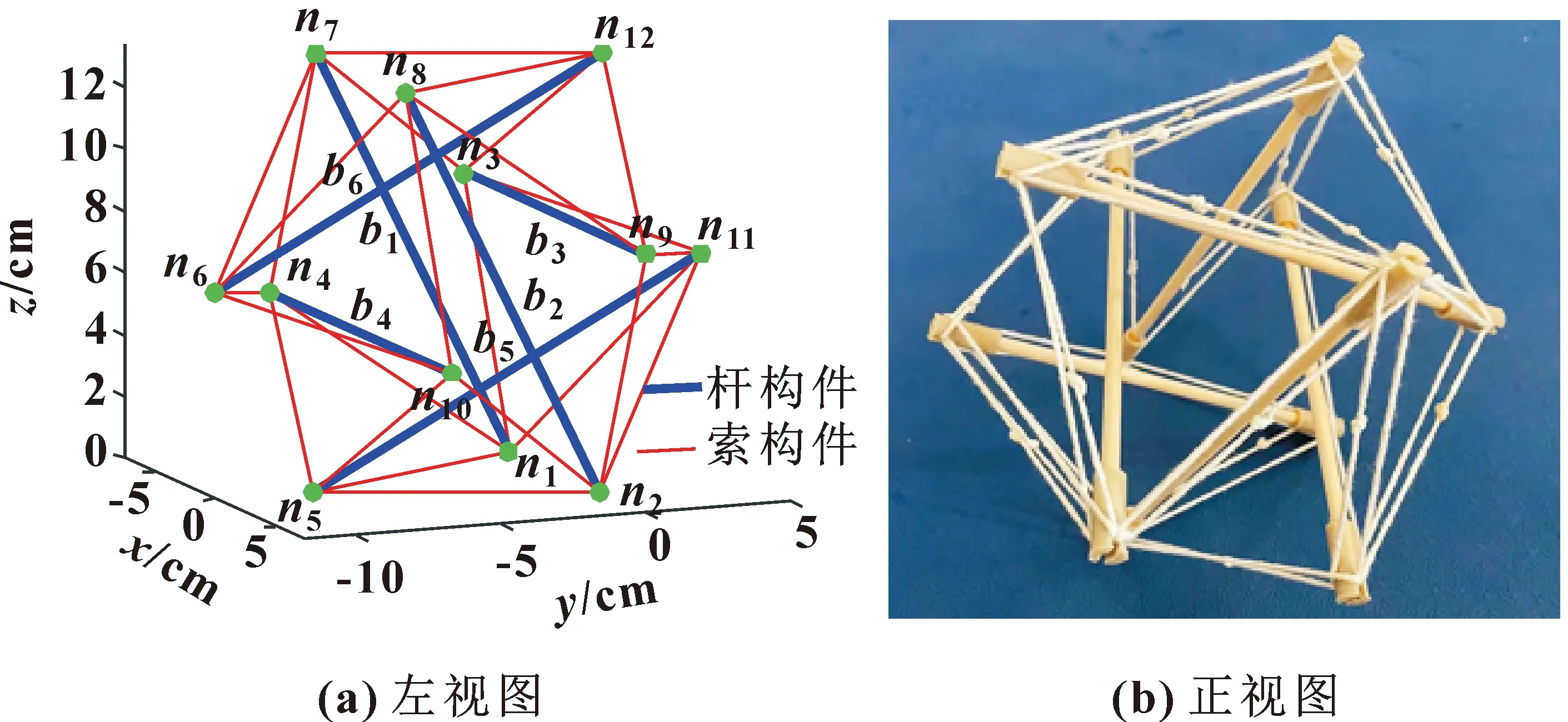
图2 六杆张拉整体结构数学模型Fig.2 Mathematical model of six-bar tensegrity structure: (a)left view;(b)front view
2 六杆张拉整体结构非线性力学特性分析
2.1 基于ANSYS的六杆张拉整体结构模型
由于张拉整体结构通过索-杆间张紧力维持平衡,预应力数值的变化会影响张拉整体结构的几何刚度矩阵,存在几何非线性问题,进而影响结构的承载刚度及结构刚度,因此在分析中需考虑这种影响。六杆张拉整体结构索、杆单元和材料的属性如表2所示。

表2 材料属性Tab.2 Material properties
在ANSYS中建立分析模型如图3所示。
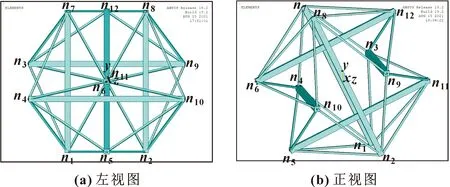
图3 六杆张拉整体有限元分析模型Fig.3 Finite element model of six-bar tensegrity structure: (a)left view;(b)front view
2.2 轴向载荷对结构变形影响
六杆张拉整体机器人应用于深空探测时,投放下落过程存在着很大的轴向载荷,这个轴压载荷对其横向振动特性影响很大,会造成压杆屈曲失效、拉索屈服失效等,从而导致探测工作失败,因此研究轴向载荷对结构变形的影响尤为重要。
为研究结构的节点位移与载荷的关系,对顶部的3个节点n7、n8和n12依次施加沿z轴负方向的轴向载荷,图4所示为施加载荷方向,橙色箭头为轴向载荷方向。
分析过程中固定模型底部的3个节点n1、n2和n5,对顶部3个节点n7、n8和n12施加沿z轴负方向的载荷,施加载荷的大小从0 N逐渐变化到7 000 N,共进行了8次模拟分析,结构变形如图5所示。其中虚线框架为变形前的模型,图中的标尺为节点位移量,红色表示节点位移量最大,蓝色最小。
在不同轴向载荷下,分析得到轴向与径向变形的变化规律,如表3所示。六杆张拉整体结构的轴向、径向变形随着轴向载荷的增加而增加,其中轴向变形从0 mm增加到0.94 mm,增幅趋势较平缓;径向变形从0 mm增加到0.28 mm,增幅趋势平缓。
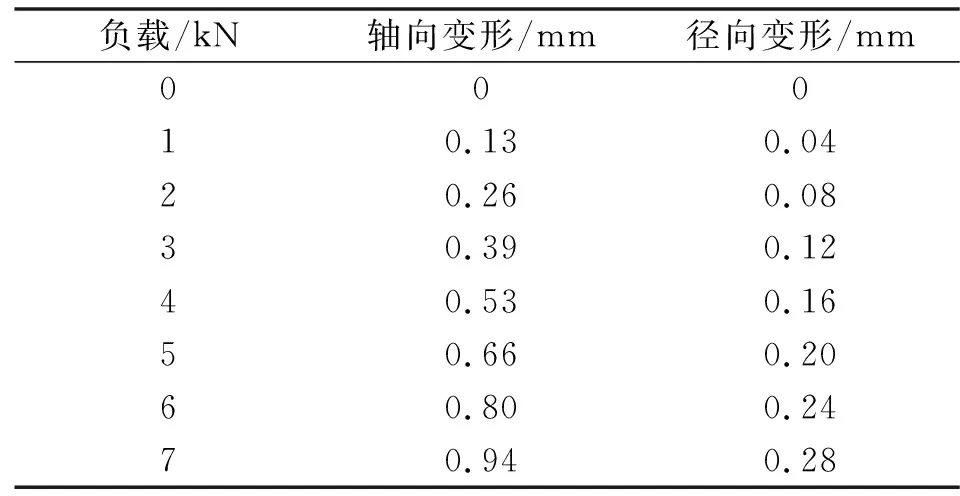
表3 不同轴向载荷下的节点最大位移量Tab.3 Maximum displacement of nodes under different axial loads
由此可得,轴向载荷对轴向、径向变形的非线性力学特性影响较小。
2.3 扭转载荷对结构变形影响
按上述研究方法,对上端面顶部3个节点连线方向依次施加扭转载荷,图6所示为施加载荷方向,黑色箭头为扭转载荷方向。
分析过程中固定模型底部的3个节点n1、n2和n5,对顶部3个节点n7、n8和n12施加扭转载荷,载荷大小从0 N·m逐渐变化到4 200 N·m,结构变形如图7所示。
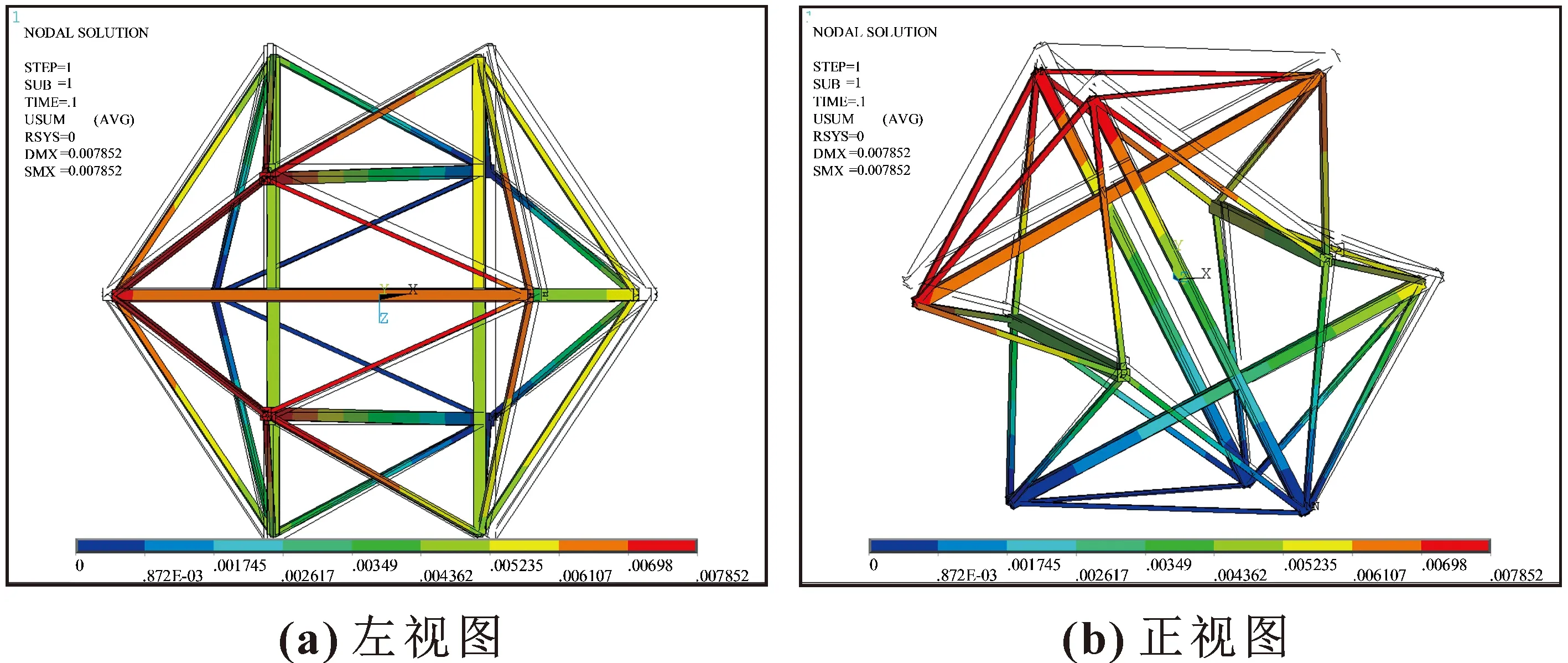
图7 扭转载荷下六杆张拉整体结构变形示意Fig.7 Deformation of six-bar tensegrity structure under torsional load:(a)left view;(b)front view
在不同扭转载荷下,分析轴向、径向及扭转变形的变化规律如表4所示。

表4 不同扭转载荷下的节点最大位移量Tab.4 Maximum displacements of nodes under different torsional loads
由表4可得:随着扭转载荷的增加,轴向变形量逐渐增加,且在0.6~3 kN·m上升速率较高,3~4.8 kN·m上升速度放缓,增幅趋势较明显;径向变形从0 mm增加到1.08 mm,增幅趋势较平缓;扭转角从0 rad增加到0.03 rad,增幅趋势平缓。
由此可得,扭转载荷对轴向变形的非线性力学特性影响大,对径向变形的非线性力学特性影响较小,对扭转角呈线性变化。
2.4 预应力对结构变形影响
为分析预应力变化对六杆张拉整体结构变形的影响,保证六杆张拉整体结构的其他参数不变,设定5组初始预应力值,通过改变索构件预应力倍数,研究预应力对六杆张拉整体结构变形的影响。
同理,对顶部的3个节点n7、n8和n12施加轴向载荷,大小恒为100 N,在不同预应力条件下,通过计算得到轴向、径向变形的变化规律,如表5所示。
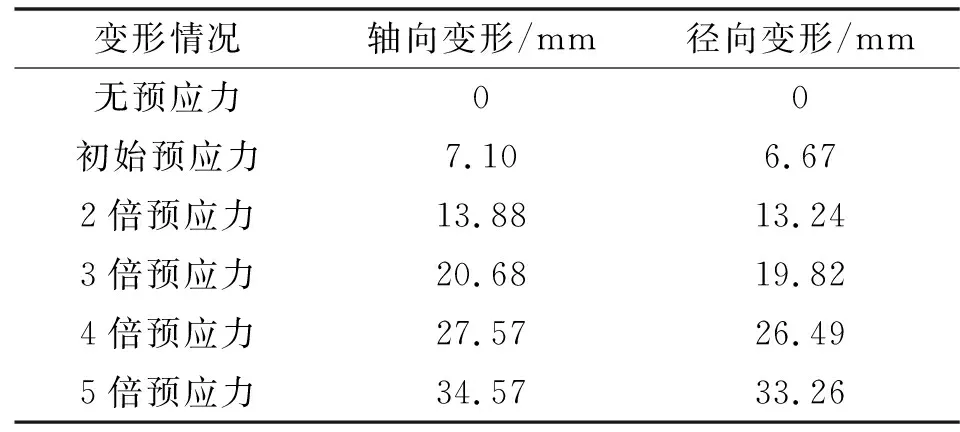
表5 轴向载荷下不同预应力对应的节点最大位移量Tab.5 Maximum displacements of nodes under different prestress with axial load
由表5可以看出:在轴向载荷下,六杆张拉整体结构的轴向、径向变形均随着预应变的增加而增加,其中轴向变形从0 mm增加到34.57 mm,径向变形从0 mm增加到33.26 mm,增幅趋势较平稳。无预应力时,结构变形量为0 mm,随着预应力成倍增加,其带来的变化并未成倍增加,增幅呈直线变化。
同理,对顶部的3个节点n7、n8和n12施加扭转载荷,大小恒为600 N·m,通过计算得到各向变形规律,如表6所示。
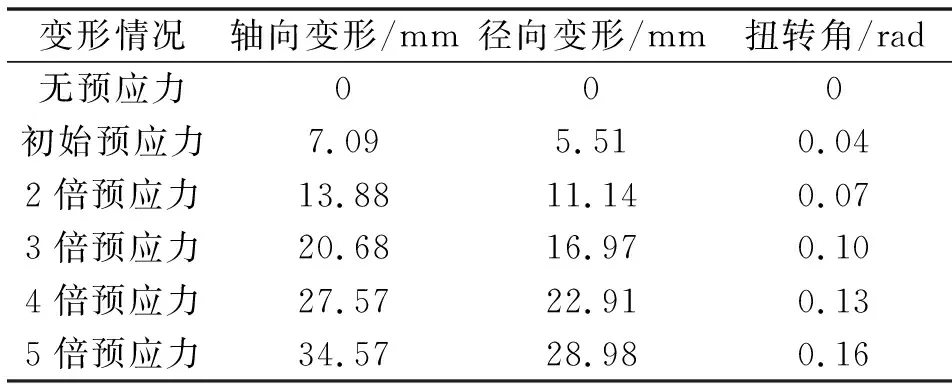
表6 扭转载荷下不同预应力对应的节点最大位移量Tab.6 Maximum displacements of nodes under different prestress with torsional load
由表6可知:在扭转载荷下,其中轴向变形从0 mm增加到34.57 mm,径向变形从0 mm增加到28.98 mm,增幅趋势较平稳,各向位移受预应力增大的影响与在轴向载荷下的情况类似,扭转角变化不明显。
该结果表明:预应力对轴向变形、径向变形及扭转变形非线性力学体系影响呈线性变化。
2.5 结构参数对结构变形影响
当构件轴向载荷保持不变时,六杆张拉整体结构的弹性刚度仅取决于结构参数,在计算过程中,由于弹性模量与横截面积是乘积关系,所以文中只作横截面积的参数分析。对顶部3个节点分别施加轴向载荷1 000 N,索杆构件分布如图8所示,同类构件截面变化对结构变形的影响如图9所示。

图8 杆索构件分布Fig.8 Distribution of bars and cables

图9 不同结构参数下节点最大位移量Fig.9 Maximum displacement of nodes under different structural parameters
在轴向载荷下,改变同类构件的横截面积,结构的轴向位移、径向位移都存在一定幅度的变化,而扭转角变化并不明显。如图9所示,其中,斜索截面积减半的影响最为明显,轴向、径向变形量分别为0.99 mm和1.04 mm,增幅最明显,在18%左右;杆截面积减半时,轴向、径向变化量分别为0.78 mm和0.62 mm,增幅较明显,在12%左右;水平索截面积减半,轴向、径向变化量分别为0.12 mm和0.13 mm,增幅不太明显,在2%左右。因此,在构件的弹性变形范围内,改变六杆张拉整体结构的构件截面尺寸对结构力学性能的影响较小。
2.6 影响因素敏感度分析
为了便于分析六杆张拉整体中结构参数对力学性能的影响,此节进行了影响因素敏感度分析。
通过因变量的相对变化与自变量的相对变化之比,定义六杆张拉整体结构各类变形量fi对结构参数xi的敏感度。
(7)
式中:fi为六杆张拉整体结构的某一变形量;xi为六杆张拉整体结构的某一结构参数;Δxi为结构参数的变化量;Δfi为结构参数变化引起的位移变化。
通过式(7)计算得出了各参数变化对六杆张拉整体结构变形量的敏感度,如图10所示。可以看出:轴向、径向变形量对预应力和载荷敏感度较高,对水平索面积敏感度则较低,扭转载荷对轴向变形量的正敏感度最高。通过以上的分析可知:在载荷不变的情况下,主动提高拉索预应力和增加斜索截面面积是改善六杆张拉整体结构力学性能的有效措施。
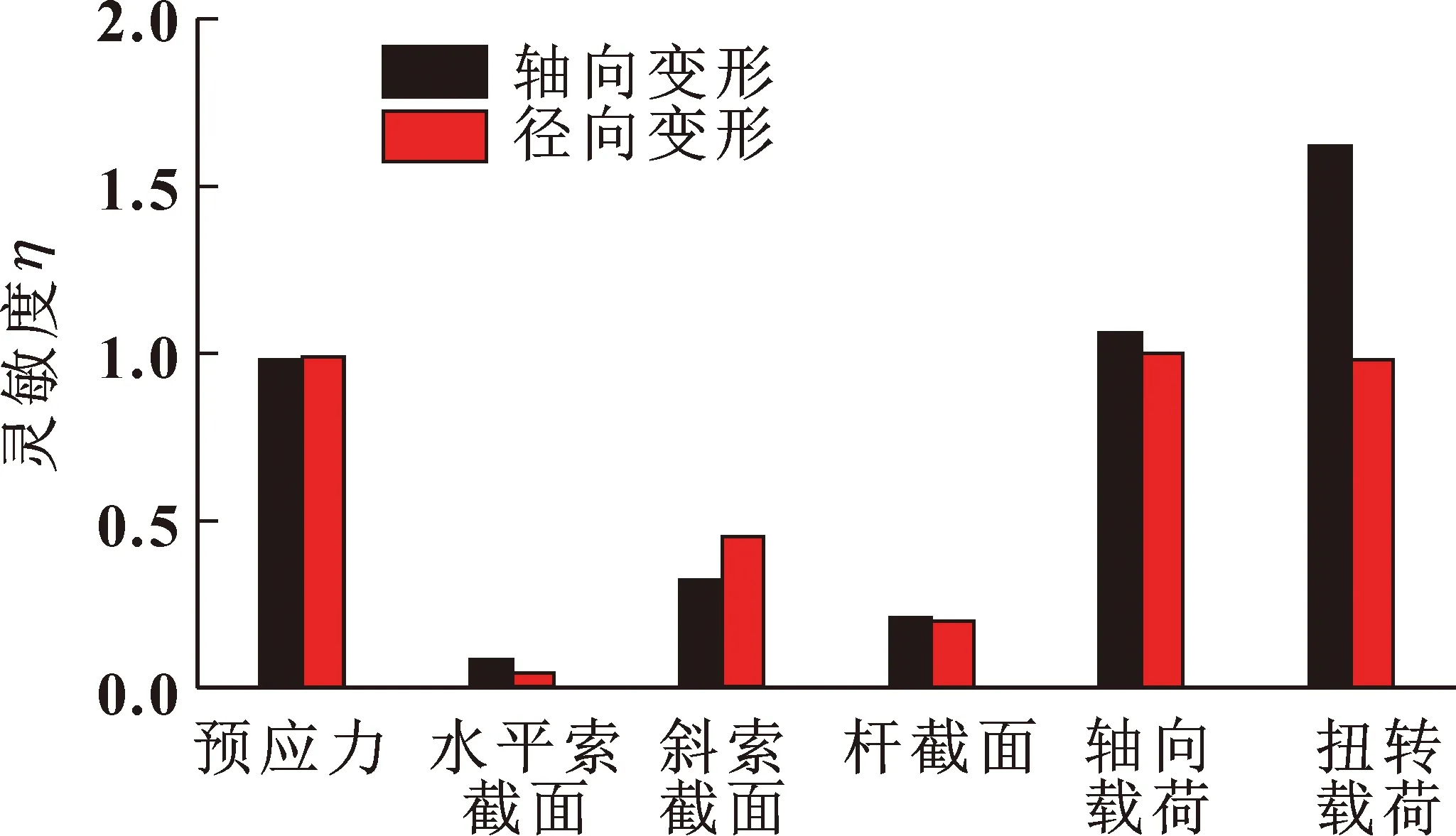
图10 节点最大位移量对结构参数的敏感度Fig.10 Sensitivity of maximum displacement to structural parameters
2.7 六杆张拉整体机器人样机实验验证
根据前面的构型设计,此节设计了六杆张拉整体机器人的控制系统,研制了样机,进行了翻滚实验,以验证前面构型的合理性。六杆张拉整体机器人样机如图11所示,机器人样机在静止状态下基本维持六杆张拉整体结构的形状,没有明显的变形。

图11 六杆张拉整体机器人实物模型Fig.11 Six-bar tensegrity robot prototype:(a)front view;(b)top view
机器人样机中的杆构件为微型推杆电机,杆长为300 mm;索构件为无弹性的凯夫拉绳和拉簧,长度为183.7 mm,平行两杆间的距离为150 mm;样机在静止状态下是几何稳定的,证明了构件之间参数关系的正确性。
实物模型搭建后,可驱动推杆电机使杆伸缩,六杆张拉整体机器人的重心发生偏移,以达到从开放三角形到封闭三角形的翻滚运动。文中对机器人样机以开放三角形着地的方式进行了翻滚实验,验证六杆张拉整体机器人结构的可动性,如图12所示。
通过前面结构设计对样机进行了研制,证明了结构参数的可行性,随后对机器人样机进行了翻滚实验,验证了六杆张拉整体机器人的可动性。该实验可作为后续机器人运动学、动力学及轨迹规划等研究开展的基础。
3 结论
(1)通过节点坐标矩阵和构件连接矩阵,建立了六杆张拉整体结构的矢量矩阵,确定了六杆张拉整体结构数学模型与结构参数之间的函数关系。
(2)通过ANSYS建立了六杆张拉整体结构的非线性力学模型,得到了不同载荷、初应变及结构参数下结构的变形规律,其中扭转载荷对结构非线性力学性能影响较大。
(3)进行了结构参数敏感度分析,结果表明:六杆张拉整体结构的非线性力学性能随着预应力和载荷的增加而增加,随着杆截面减少而减小,随着索截面减少而减少,其中预应力对六杆张拉整体结构非线性力学性能的提高较为明显。该结果对六杆张拉整机器人力学性能的提升具有较高的应用价值。
(4)搭建了六杆张拉整体机器人样机模型,进行了机器人样机的翻滚运动测试,为后续机器人运动学、动力学及轨迹规划提供了参考。
