基于拓扑优化的变密度蜂窝结构参数化设计及冲击性能研究

2023-12-01徐峰祥徐智钊蒋舟顺

振动与冲击 2023年22期

邹震, 徐峰祥, 徐智钊, 蒋舟顺

(1. 武汉理工大学现代汽车零部件技术湖北省重点实验室,武汉 430070;2. 武汉理工大学汽车零部件技术湖北省协同创新中心,武汉 430070)

蜂窝结构是一种高空隙率、轻质的新型结构,具有高比强度/刚度、减震降噪、冲击吸能及可设计性等优势,在建筑、汽车、铁路车辆、船舶、航空航天、卫星、包装和医疗植入物等领域具有广泛的应用前景[1-3]。近年来,随着汽车安全性与轻量化的冲突不断加剧[4-6],对具有优异吸能特性的蜂窝结构的冲击性能研究已成为热点。

在蜂窝结构冲击性能和轻量化的协同设计方面,理论上可行的方法为材料替换和设计优化。其中,材料替换是指用性能更加优越的材料替换性能较差的材料以提升蜂窝的力学性能。除常用的铝合金蜂窝结构,相继出现了不锈钢[7]、钛合金[8]、非金属材料(玻璃纤维[9]、Nomex[10]、聚乙烯[11]、植物纤维[12]等)蜂窝结构。更换蜂窝结构的材料是实现其性能提升的有效手段,但不可避免地会提升蜂窝结构的造价,难以适用于汽车、包装等民用行业。蜂窝结构的设计优化又可细分为单胞优化设计和梯度分布增强设计。其中,在蜂窝结构的新型单胞设计方面,已涌现出填充型[13-14]、嵌套型[15]、负泊松比型[16-17]等多种新型蜂窝结构,这些结构均通过局部或整体加强的方式有效地提升了蜂窝的力学性能,但同时也增大了其结构的复杂程度,提升了其加工难度。

蜂窝结构的分布增强设计是指在不改变单个蜂窝胞元结构的前提下,对其按照某一规律进行梯度设计,从而实现其结构的整体有序、充分变形。梯度分布增强设计作为提升蜂窝结构冲击性能的有效方式之一,国内外学者对此开展了大量研究,Hu等[18]采用将规则蜂窝边用二级蜂窝替代一级蜂窝边的方法构建了新型自相似梯度蜂窝,实现了其综合耐撞性能的提升;Zhang等[19]研究不同密度梯度的蜂窝结构的吸能性能,确定了蜂窝结构最优密度梯度排布方式;马芳武等[20]提出了一种仿生自相似分层蜂窝结构,实现了蜂窝在多种碰撞工况下的稳定变形;袁敏等[21]研究了厚度梯度的负泊松比蜂窝结构的耐撞性能,确定具有正向厚度梯度的内凹六边形蜂窝具有更好能量吸收和冲击性能;乔及森等[22]采用改变六边形蜂窝壁角的方法构建了一种串联梯度蜂窝结构,实现了通过改变梯度率的方法控制串联梯度蜂窝变形模式。但上述蜂窝梯度分布增强设计一般都是基于设计人员的工程经验,进行蜂窝的“阶梯”式梯度设计,无法实现连续梯度设计,难以最大限度地发挥梯度排布对蜂窝结构力学性能的提升效果。

拓扑优化是指通过优化给定设计区域内的材料分布形式,以同时提升目标结构的力学和轻量化性能的方法。已有学者将拓扑优化方法应用在蜂窝结构的动力特征拓扑优化,Zhang等[23]将优化的连续参数(密度)映射到点阵结构参数(支柱直径)上,获得非均质蜂窝结构;Jia等[24]利用拓扑优化密度信息设计了正方形蜂窝结构;邢昊等[25]利用拓扑优化密度映射法设计了一种非均质六边形蜂窝,并通过试验证实了其设计方法能提升结构的静态刚度;赵芳垒等[26]基于体素化的方法,验证了设计的非均质蜂窝与拓扑优化的目标蜂窝之间的差异。上述研究为蜂窝结构的拓扑优化研究奠定了基础,但目前拓扑优化蜂窝的面内冲击性能仍存在不足,且缺乏拓扑优化参数对蜂窝结构面内冲击性能影响的系统性研究。

本文基于变密度拓扑优化方法,提出一种拓扑优化密度映射蜂窝(以下简称拓扑蜂窝)。通过参数化建模创建拓扑蜂窝的结构模型,并采用有限元分析的方法分别探究在不同的冲击速度下,映射系数、相对密度对拓扑蜂窝的面内冲击变形模式、动态响应和能量吸收性能的影响,并与等质量标准蜂窝进行冲击性能的对比,探究将拓扑优化方法引入蜂窝结构的梯度设计对其冲击性能的提升效果。

1 拓扑蜂窝的结构参数化设计

1.1 蜂窝结构参数

如图1所示,对于正六边形蜂窝胞元,其结构参数可由蜂窝胞元外边长度a(简称胞元边长)和胞元内边长度bi表示,定义第i个蜂窝胞元的相对密度为ρi,胞元的相对密度为胞元面积s1和内部六边形面积s2的差值与胞元面积s1的比值,因此,胞元相对密度可表示为

图1 蜂窝胞元结构参数Fig.1 Cellular parameters of honeycomb structures

(1)

由式(1)可知,蜂窝胞元的相对密度仅与胞元内外边长度相关。参考传统均质蜂窝结构的胞元的结构尺寸,为实现将拓扑蜂窝的实际材料分布按照拓扑优化材料分布结果进行设置的研究目标。将所有的胞元外边长度均设置为常数a,通过调整内边长bi完成蜂窝相对密度的调整,从而实现拓扑蜂窝内部材料的分布调整。

1.2 参数化设计流程

蜂窝结构复杂、设计变量较多等,传统建模方法难以满足其建模需求。因此,本文采用参数化设计方法,通过SolidWorks的二次开发模块高效建立拓扑蜂窝的实体模型。拓扑蜂窝结构的参数化设计流程图,如图2所示。在设计过程中,首先设定设计域的尺寸、相对密度、蜂窝胞元尺寸及拓扑单元尺寸,并基于这两种单元分别对设计域进行离散,记录每个胞元和拓扑单元的中心坐标,获取胞元与拓扑单元的距离关系,确定胞元的相对密度和内边长度,生成胞元模型并循环上述过程,直到整个设计域的所有胞元计算完成。

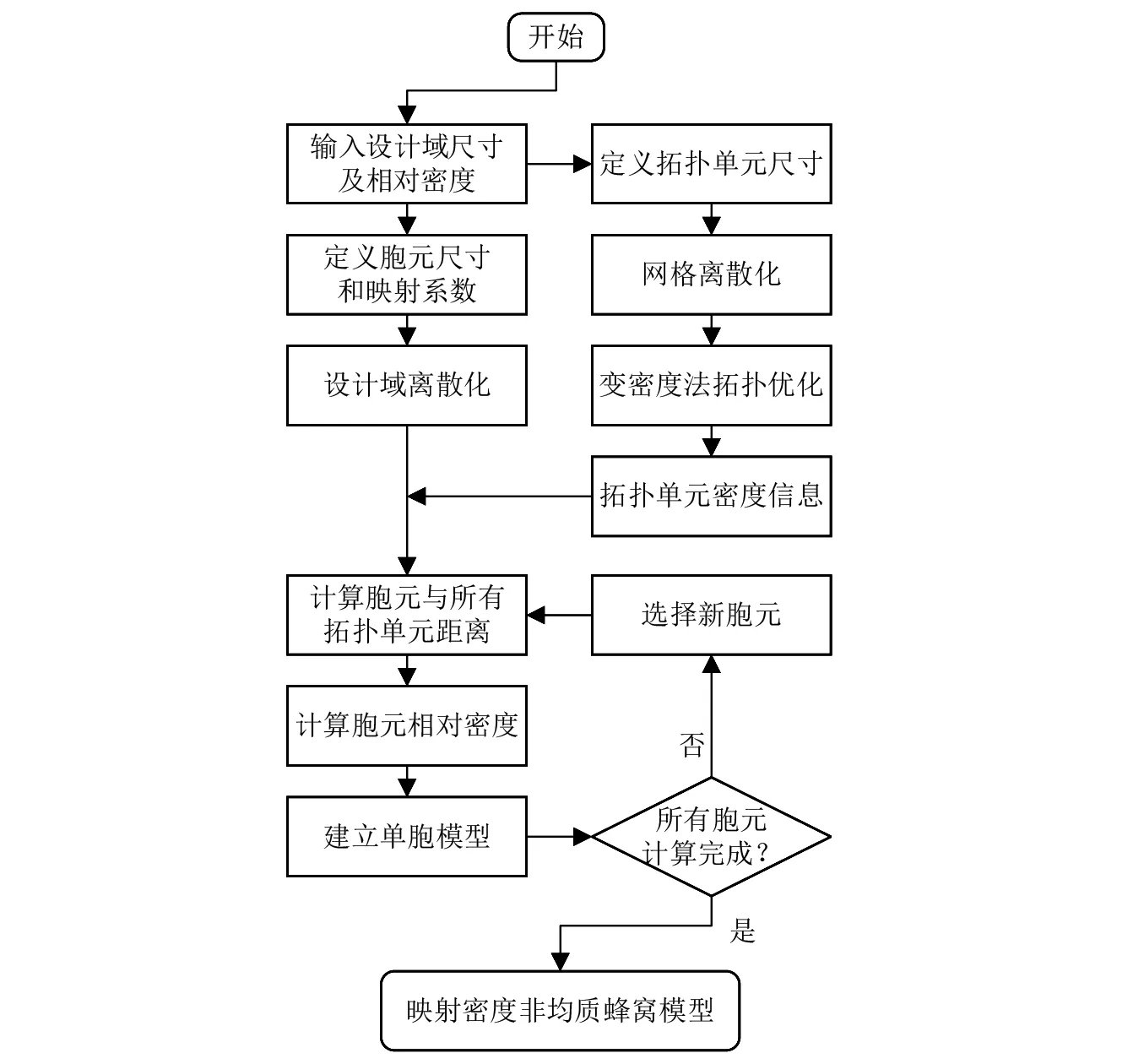
图2 拓扑蜂窝的参数化设计流程图Fig.2 Flowchart of density mapping cellular parametric design

1.3 参数化设计实施过程

拓扑优化问题可以描述为:在给定体积约束的条件下,使目标结构柔度最小,寻求此时最优的单元密度分布。基于固体各向同性材料惩罚模型(solid isotropic material with penalization,SIMP)变密度法的拓扑优化模型可以描述为[27]

(2)

式中:P为载荷向量;U为位移向量;K为总体刚度矩阵;ke为单元刚度矩阵;x为密度矩阵,由拓扑优化的微单元密度xi组成,单元总数为N;V0为结构体积的约束上限。求解优化模型得到体积约束下的密度矩阵,由密度矩阵可得拓扑微单元密度分布。本文采用拓扑优化密度映射方法,设置较小的惩罚系数以消除其对中间密度单元的影响。基于拓扑优化的单元密度信息,计算蜂窝胞元的相对密度,实现拓扑优化灰度单元密度信息的充分利用。

首先设置设计域边界条件,随后通过拓扑优化算法获取微单元的相对密度分布,最终确定了蜂窝单元与拓扑单元映射关系,如图3所示。设第i个六边形蜂窝胞元的中心坐标为(xi,yi),第j个拓扑微单元的中心坐为(xj,yj),则两单元之间的距离可表示为

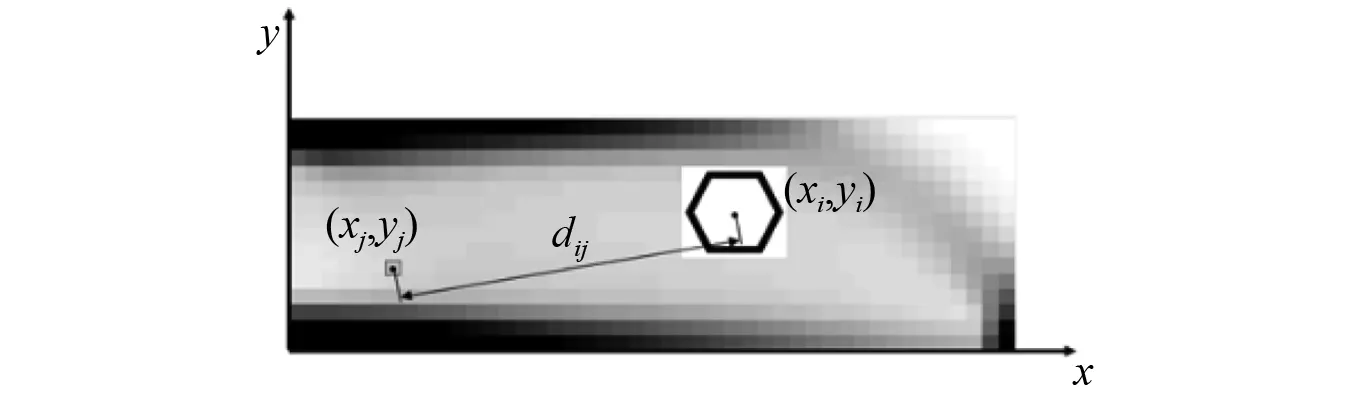
图3 蜂窝单元与拓扑单元映射关系Fig.3 The mapping relationship between cellular units and topological units

(3)

基于反距离加权平均法,综合计算每个拓扑微单元对蜂窝胞元的影响,且离蜂窝单元越近的拓扑单元影响权重ω越大,映射函数可以定义为

ω(dij)=e-k×(dij)

(4)

式中,k为映射系数,其反映了映射过程中距离对权重的影响。k值对距离的权重影响如图4所示。由图4可以发现,k值越大,距离较小的单元具有的权重也越大。

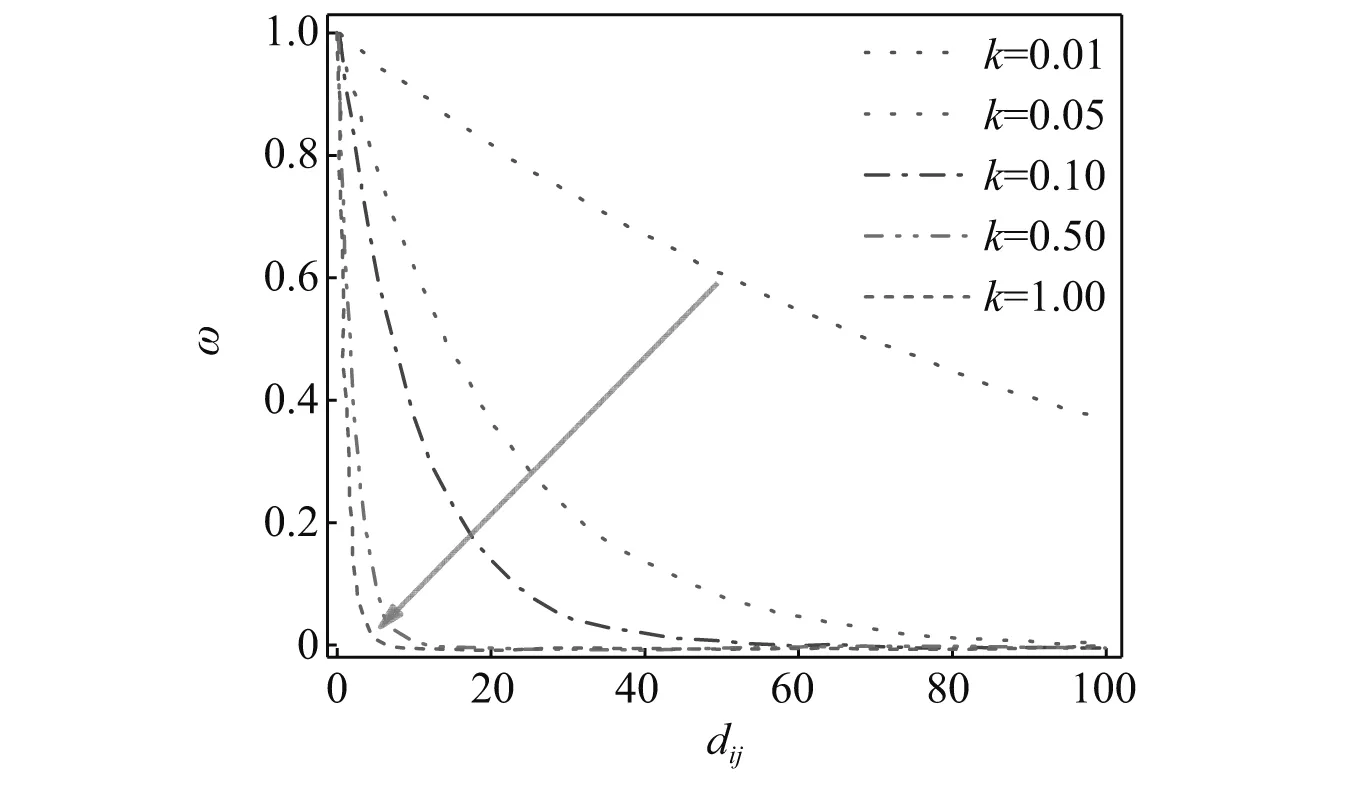
图4 不同映射系数下距离对权重的影响Fig.4 Influence of distance on weight under different mapping coefficients

结合拓扑优化的结果,将第j个拓扑微单元的相对密度定义为xj,第i个蜂窝胞元的映射密度定义为ρi,则胞元映射密度为

(5)

式中,N为拓扑微单元的数量。根据本文1.1节对蜂窝胞元的参数分析可知,蜂窝胞元的外边长度a设为常数,通过调整蜂窝胞元的内边长度bi即可实现拓扑蜂窝内部材料的分布调整。另外,为保证拓扑蜂窝整体结构的连续性,将蜂窝胞元壁厚的取值范围设置为0.25～1.10 mm。

2 计算模型

2.1 几何模型

拓扑蜂窝受面内冲击时的示意图如图5(a)所示,将拓扑蜂窝置于上、下两刚性板之间,加载时,底部刚性板固定,上端刚性板以恒定速度v向下冲击试件。基于拓扑蜂窝面内冲击的受力特点,拓扑优化模型可以等效为如图5(b)所示的受力模型。拓扑蜂窝结构的底端固定,上表面受均布压力P加载。通过拓扑优化程序设置结构边界条件,并将结构优化目标体积设置为原体积的20%。如图5(c)所示,经过迭代,获得下表面固定、上表面均布压力加载条件下的拓扑优化单元的密度分布矩阵。将密度分布矩阵对应的密度值映射到具体的蜂窝胞元,此时被映射的密度值就是映射密度。随后,映射密度通过映射系数转换为对应蜂窝胞元的相对密度,并最终通过式(1)确定胞元的具体壁厚,从而实现拓扑蜂窝的实际材料分布与拓扑优化结果相一致的设计目标。映射密度、相对密度和蜂窝结构的实际材料分布之间的关系可表示为:映射密度将拓扑优化结果转换为蜂窝结构胞元的相对密度,实现蜂窝结构拓扑优化设计的可行性。蜂窝胞元基于其对应的相对密度确定具体的壁厚,实现蜂窝结构的内部材料拓扑优化合理分布。

图5 拓扑蜂窝结构设计Fig.5 Design of topology optimization honeycomb structures

为研究相对密度ρ和映射系数k对拓扑蜂窝面内冲击性能的影响,相对密度ρ分别为0.12,0.16,0.20和0.24,映射系数k分别为0.01,0.05,0.10和0.50。此外,为便于对比分析将拓扑优化方法引入蜂窝设计对其冲击性能的提升效果,参照Ruan等[28]对标准蜂窝冲击性能的研究,将拓扑蜂窝的胞元尺寸a设置为5 mm。基于拓扑蜂窝结构的参数化建模方法,构建的4种拓扑蜂窝结构的几何模型如图6所示。由图6可以发现,拓扑蜂窝的整体质量随相对密度ρ增大而增大,这是由于相对密度ρ增大、蜂窝内边长度bi减小造成胞元壁厚增大。此外,也可以发现拓扑蜂窝的壁厚差异随映射系数的减小而减小,这是由于随着映射系数的减小,距离对相对密度的影响也在逐渐减弱,最终呈现了拓扑蜂窝胞元之间的壁厚差异逐渐减小。当映射系数k越大,拓扑蜂窝结构的两侧胞元壁厚与中部胞元的差值也越大。拓扑蜂窝整体呈现出中部胞元壁厚小于外部壁厚,位于冲击端的胞元壁厚小于固定端胞元壁厚。

图6 拓扑蜂窝几何模型Fig.6 Geometry of density mapping honeycomb

2.2 有限元模型

考虑到当映射系数较小时,拓扑蜂窝的几何模型包含较多薄壁实体,难以采用实体单元进行有限元分析。因此,本文采用软件Hypermesh/ABAQUS联合仿真的方法,首先将生成的拓扑蜂窝几何实体导入Hypermesh软件中抽取中面,并选用SHELL163薄壳单元进行离散,将不同的壁厚单元归类为不同的属性,这种建模方法可以较好地保留原始几何实体的壁厚特征。为保证计算精度和收敛性,沿厚度方向定义5个积分点。此外,经过多次试算和灵敏度分析,模型的网格尺寸确定为0.7 mm。研究表明,蜂窝结构在宽度(x)和高度(y)方向的胞元数目分别超过10时,结构的动态响应更加稳定[29]。因此,为有效捕捉拓扑蜂窝试件的面内动态响应特征,其宽度(x)和高度(y)方向分别设置了11个和10个胞元,对应拓扑蜂窝的宽度和高度分别为85.5 mm和86.5 mm,面外厚度设置为4 mm。最终通过软件ABAQUS/Explicit对拓扑蜂窝模型进行非线性动态显式求解。蜂窝单元底部与刚性板绑定。所有的接触面均设置为通用接触,定义摩擦因数为0.15。压缩距离限制为初始距离的80%。拓扑蜂窝的面内冲击有限元模型如图7所示。对壳单元进行厚度渲染后,观察细节放大图可以发现,拓扑蜂窝胞元的壁厚特征得以较好的体现。

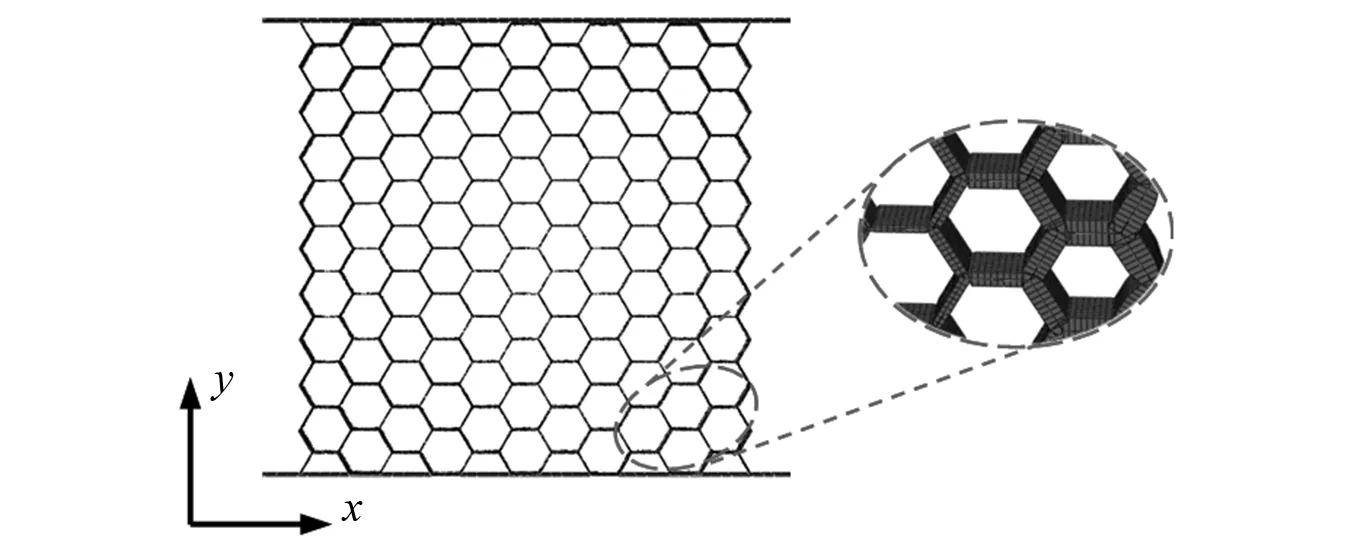
图7 拓扑蜂窝面内冲击模型示意图Fig.7 Schematic diagram of the topology optimization honeycomb under in-plane impact

拓扑蜂窝基体材料设置为铝,采用理想弹塑性本构模型,具体材料参数如表1所示。

2.3 模型可靠性

为验证本文有限元模型的可靠性,构建了与Ruan等研究中一致的标准蜂窝模型,并分别选择在冲击速度为3.5 m/s和14.0 m/s时进行可靠性验证。以分析模型在不同冲击速度下的准确性与可靠性。仿真得到的蜂窝结构变形模式和力-位移曲线,如图8所示。结果显示:当冲击速度为3.5 m/s时,本文仿真模型和Ruan等的研究模型在峰值应力(PCF)的误差为 4.4%,平台应力的误差为7.9%;当冲击速度为14.0 m/s时,本文仿真方法与Ruan等的研究模型在峰值应力的误差为7.0%,平台应力的误差为5.2%。此外,本文采用的仿真方法也较为准确地预测了蜂窝结构在3.5 m/s和14.0 m/s冲击下的变形模式。综上,结果表明本文采用的仿真方法在预测蜂窝结构的冲击性能和变形模式上均具有较高的可靠性,可用于后续的研究。

为进一步确定仿真模型的有效性,对模型的沙漏能进行分析。以k=0,ρ=0.24的拓扑蜂窝模型为例,其在仿真过程中的能量变化曲线如图9所示。由图9可以看出,冲击过程中的沙漏能和滑移能均较小,滑移能与伪应变能之和与内能之比小于5%,这进一步印证了本文有限元模型的可靠性。

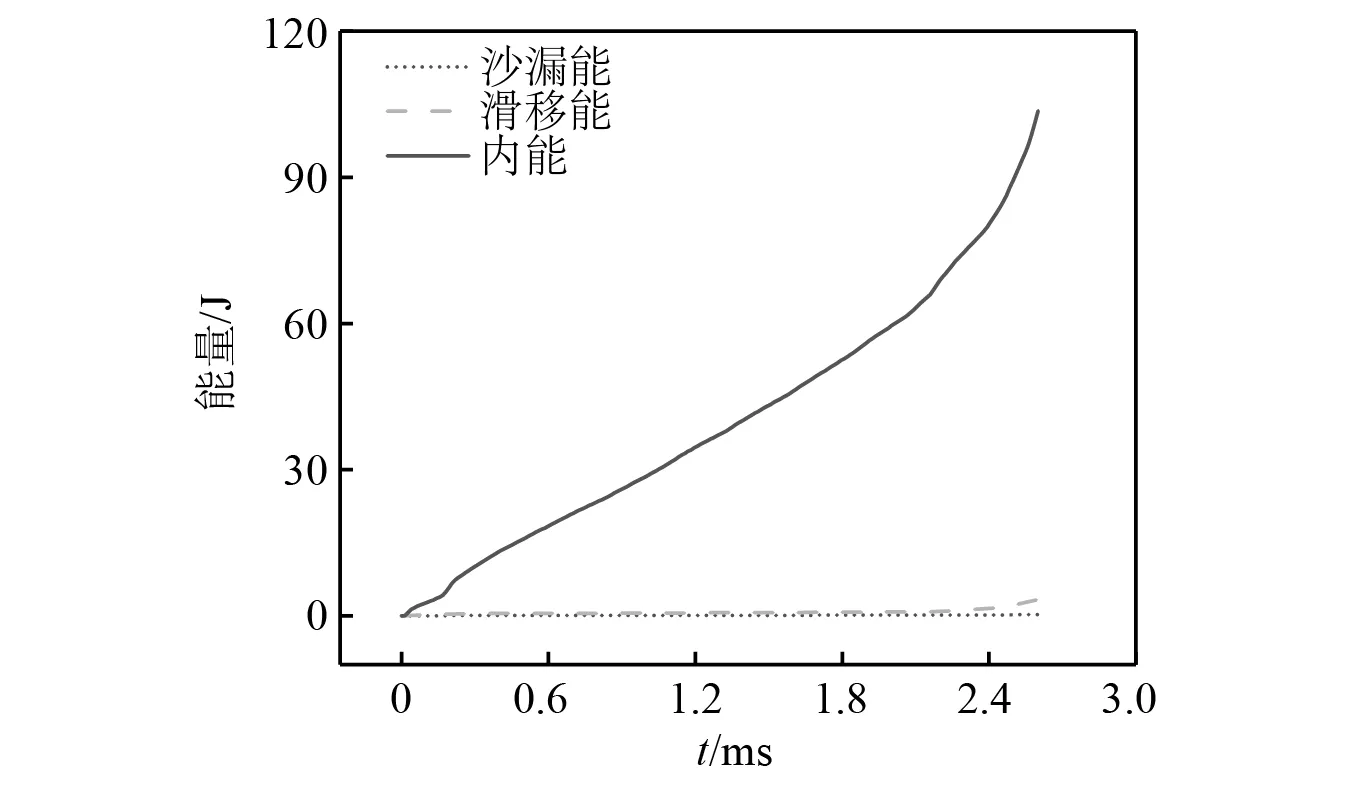
图9 拓扑蜂窝面内冲击时的能量变化曲线Fig.9 Energy change curve of topology optimization honeycomb in-plane impact

3 结果与分析

3.1 变形模式

当k=0.10,ρ=0.20时的拓扑蜂窝,在两种不同冲击速度时的典型变形模式如图10所示。定义刚性板的冲击端位移与蜂窝初始高度的比值为名义应变ε。从图10中可以看出,冲击速度对蜂窝结构的面内变形模式有显著影响,当冲击速度较低时(v=10 m/s),压缩初始,蜂窝结构在冲击端出现局部弯曲变形,随后变形呈“X”型,并随压缩过程稳定向固定端传递,直至整个模型趋于密实。当冲击速度提高到90 m/s时,蜂窝的变形模式发生较大变化,由整体变形转变为局部压缩变形。类似于均质六边形蜂窝结构,蜂窝变形区域只集中在冲击端,呈“I”型变形模式,并逐层向下渐进压溃,直至结构整体趋于密实。

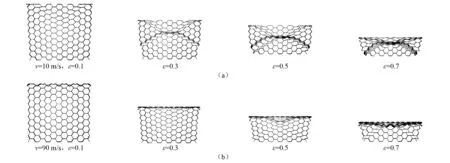
图10 拓扑蜂窝结构的宏观变形模式Fig.10 Macroscopic deformation modes of topology optimization honeycomb structure

3.1.1 不同冲击速度下的变形模式

具有不同映射系数的拓扑蜂窝在不同冲击速度下的变形模式,如图11所示,此时拓扑蜂窝的名义应变ε=0.3。如图11(a)所示,在v=3 m/s、映射系数k=0.50时,蜂窝的变形模型呈现向冲击端开口的“V”型; 当k=0.10时,变形模式转变为覆盖整个蜂窝区域的“X”型变形;而当k=0.01时,蜂窝结构呈方向与k=0.50相反、向固定端开口的“V”型变形,这证明了映射系数对拓扑蜂窝的压缩变形模式有较大影响。对其在不同冲击速度下的变形模式差异的原因进行分析。以映射系数分别为0.50和0.01的拓扑蜂窝“V”形变形带开口完全相反为例,拓扑蜂窝的“V”形变形开口相反的变形模式主要是因为不同映射系数的拓扑蜂窝固定端与冲击端的胞元存在壁厚差异。当映射系数k=0.50时,拓扑蜂窝固定端壁厚大于冲击端,因此,此时的开口为冲击端方向;而当k=0.01时,拓扑蜂窝固定端与冲击端的壁厚差异较小,此时壁厚较弱的固定端先发生压溃,变形开口方向为固定端方向。

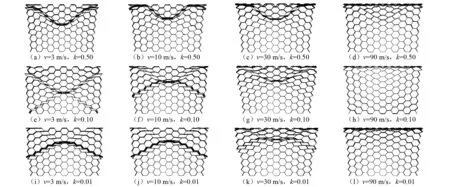
图11 拓扑蜂窝结构在不同冲击速度下的变形模式(ρ=0.20, ε=0.3)Fig.11 Deformation modes of topology optimization honeycomb under different impact velocities (ρ=0.20, ε=0.3)

随着冲击速度的提高,当v=10 m/s时,惯性效应的影响开始凸显,各拓扑蜂窝的变形模式相比于v=3 m/s更加靠近冲击端,且变形区域也在缩小。映射系数k=0.50的拓扑蜂窝,在v=10 m/s冲击下的“V”变形带要小于其在v=3 m/s时的变形带,且映射系数k=0.10的蜂窝,在v=10 m/s冲击下的“X”要高于其在v=3 m/s冲击下的“X”变形带,这均归因于冲击速度的增大带来的惯性效应。值得注意的是,由于拓扑优化设计为蜂窝结构的固定端胞元设置了较大壁厚,因此,在v=3 m/s和v=10 m/s的冲击下,拓扑蜂窝位于固定端的胞元均未发生明显变形。

当v=30 m/s时,拓扑蜂窝变形模式相比低速冲击时发生了明显变化。各蜂窝的变形区域相较于低速冲击时的进一步缩小,且更靠近冲击端。对比图11(f)和图11(g)可以发现,映射系数k=0.10的拓扑蜂窝由低速时的“X”型变形模式转变成了“V”型变形,且变形区域进一步集中,这主要是由冲击速度增大带来惯性效应的影响。但映射系数k=0.50的拓扑蜂窝,在v=10 m/s和v=30 m/s冲击速度下的变形,模型却未发生明显变化,这一现象合理的解释是随着映射系数的增大,蜂窝结构的两侧胞元壁厚和强度增大,增大的冲击速度未造成其被压溃,而当映射系数k=0.10时,两侧壁厚增大不明显,在v=30 m/s冲击速度下被压溃。当冲击速度的进一步增大至90 m/s时,惯性效应的影响进一步增强,各拓扑蜂窝结构均呈现沿冲击方向的“I”字状变形模式,变形随刚性板下压而逐层向固定端递进,这种高速冲击下的拓扑蜂窝变形模式同标准均质六边形蜂窝相似。

通过以上分析可知:映射系数、冲击速度对拓扑蜂窝的面内变形模式具有较大影响。当映射系数较大时,拓扑蜂窝结构的两侧蜂窝的壁厚大于中部壁厚,固定端壁厚大于冲击端壁厚;而当映射系数较小时,拓扑蜂窝两侧胞元与中部胞元的壁厚差异、固定端与冲击端胞元的壁厚差异均减小。因此,在中低速冲击时,映射系数的变化造成了蜂窝结构的变形模式从“V”型转为“X”型,并最终转为反方向的“V”型变形。而随着冲击速度增大,惯性效应增强,拓扑蜂窝的变形模式也发生了改变,具体体现为变形区域进一步缩小,且更加靠近冲击端。此外,经分析可以发现冲击速度越大,映射系数对拓扑蜂窝的影响则越小。当冲击速度v=90 m/s时,惯性效应主导了变形模式,所有拓扑蜂窝的变形趋于一致呈“I”形,此时映射系数对变形模式的影响较小。

3.1.2 不同相对密度下的变形模式

当面内冲击速度为30 m/s、映射系数k=0.10,相对密度ρ分别为0.12,0.16,0.20和0.24时,拓扑蜂窝在名义应变ε=0.4时的变形模式,如图12所示。由图12可以发现,相对密度较小的拓扑蜂窝在冲击端的变形相比相对密度较大的拓扑蜂窝变形范围更小,并最终在相对密度为0.24时转变为“X”变形。这主要是由于当相对密度较小时,蜂窝的整体壁厚较小,此时在受到冲击时其变形更加集中,变形区域较小,呈现出局部的变形模式。而随着相对密度进一步增大,其变形区域开始缓慢增大,并最终在相对密度为0.24转变为全局变形。

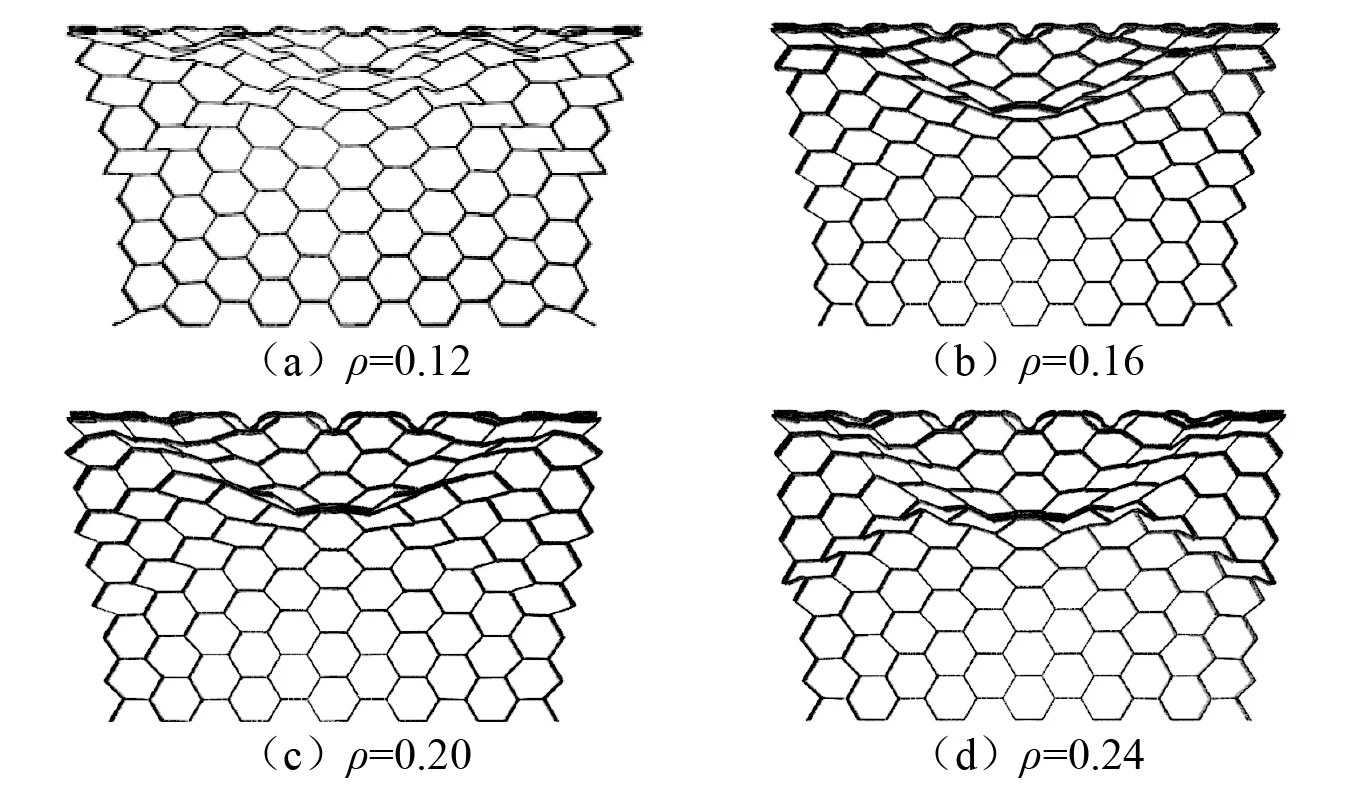
图12 不同相对密度的拓扑蜂窝结构变形模式Fig.12 Deformation modes of topology optimization honeycomb structures with different relative densities

3.2 动态响应分析

当蜂窝面内压缩时,其名义应力σ和名义应变ε分别可定义为

(6)

式中:F为上刚性板的压缩支反力;b为蜂窝在面外方向的厚度;δ为蜂窝的压缩位移;L和W分别为蜂窝面内长度和高度。

当相对密度ρ=0.24时,不同映射系数拓扑蜂窝的面内冲击响应曲线,如图13所示。由图13可知,拓扑蜂窝和常规均质蜂窝的动态响应相似,即初始时刻的线弹性变形阶段,在峰值冲击力后,进入应力起伏相对较小的平台阶段和最终逐渐密实的应力陡升阶段。

当低速冲击(v=3 m/s)时,不同映射系数的拓扑蜂窝的应力曲线尤其平缓,从弹性屈服后应力呈稳定上升的趋势,没有出现较大的初始峰值应力。其中,值得注意的是映射系数较大(k=0.50)的拓扑蜂窝,其应力曲线明显高于其他拓扑蜂窝。此外,映射系数k=0.50时拓扑蜂窝应变曲线波动高于其余映射系数拓扑蜂窝的应力曲线,这主要是由于随着映射系数增大,蜂窝两侧胞元的壁厚大于中部胞元的壁厚、固定端胞元的壁厚大于冲击端胞元的壁厚,造成拓扑蜂窝在压缩时呈现不连续的压溃,从而造成其应力曲线波动较大,而当映射系数较小时,拓扑蜂窝整体壁厚的差异不大,应力曲线的波动则明显减小。因此,可以合理得出增大拓扑蜂窝的映射系数是提高其应力曲线的有效方法之一。

如图13(b)和图13(c)所示,随着冲击速度增加(v=10 m/s和v=30 m/s),蜂窝的初始峰值应力明显增大,且整体应力水平也有一定提高,应力曲线波动起伏程度明显变大,此时映射系数较大的拓扑蜂窝仍然表现出更高的应力水平。当高速冲击时(v=90 m/s),蜂窝出现非常高的初始应力峰值,且整个冲击过程中应力变化非常剧烈,直到设定的压缩距离都没出现明显密实阶段,说明受惯性效应影响,蜂窝结构的压溃材料都紧紧堆积在冲击端,密实阶段相对出现得更晚。

当相对密度ρ=0.12时,4种不同映射系数蜂窝的面内响应曲线,如图14所示。由图14可以发现,当相对密度ρ均为0.12时,在不同冲击速度下,映射系数对应力曲线无明显影响。但值得注意的是,当映射系数较大的拓扑蜂窝的应力曲线波动随冲击速度的增大而增大。合理的解释是,映射系数较小时,蜂窝结构的材料分布相对均匀,因此在不同的冲击速度下呈现均匀的局部变形,应力曲线无明显波动;而当映射系数较大时,材料主要分布于蜂窝两侧,形成了强度较大的两侧区域,此时蜂窝在高速冲击时出现了较大的应力波动。在冲击速度达到90 m/s时,应力曲线在某些时刻出现接近0的现象,且主要发生在应变较小的位置,对此合理的解释是,当蜂窝受到高速冲击时,部分胞元被迅速压溃,随着蜂窝胞壁连接处屈服,冲击端受力存在短暂的延迟。

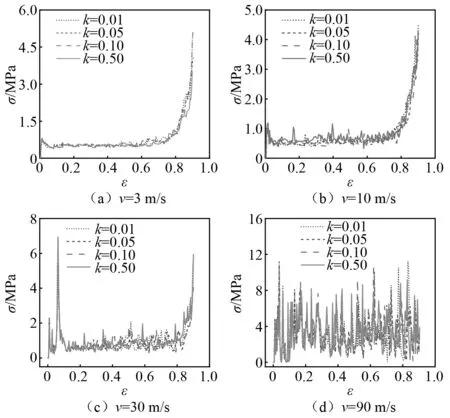
图14 拓扑蜂窝结构名义应力应变曲线(ρ=0.12)Fig.14 Nominal stress-strain curves of topology optimization honeycombs(ρ=0.12)

3.3 平台应力与能量吸收特性

蜂窝应力应变曲线的平台阶段是决定蜂窝能量吸收性能的关键阶段,反映了蜂窝结构的平均吸能水平,当压缩位移相同时,较大的平台应力意味着优异的能量吸收能力,蜂窝的平台应力可定义为

(7)

式中:εcr为屈服应变,表示在初始应力峰值时对应的名义应变;εd为锁定应变,表示蜂窝名义应力再次达到初始应力峰值时的名义应变;σε为随应变变化的名义应力。

冲击速度对各映射系数的拓扑蜂窝的平台应力影响曲线,如图15所示。由图15可以看出,随冲击速度的提高,各映射系数的拓扑蜂窝结构平台应力都有所增大。其中,值得注意的是,在相同的冲击速度下,映射系数为0.01,0.05和0.10的拓扑蜂窝之间的平台应力无明显差异,而当映射系数为0.50时,拓扑蜂窝的平台应力明显增大,也预示了蜂窝的能量吸收能力获得一定的提升。因此可以得出增大拓扑蜂窝的映射系数可使其材料分布更为合理,进而提升拓扑蜂窝的平台应力,而当映射系数较小时,拓扑蜂窝内部胞元的壁厚差异不明显,平台应力未产生明显的增大。

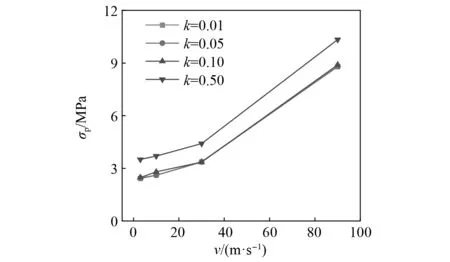
图15 不同映射系数下蜂窝平台应力随冲击速度的变化Fig.15 Variation of honeycomb platform stress with impact velocity under different mapping coefficients

拓扑蜂窝的平台应力在各冲击速度下随映射系数的变化曲线,如图16所示。由图16可以发现,在相同的冲击速度下,随着映射系数的增大,拓扑蜂窝结构的材料分布更为合理,其平台应力获得了一定的提升。此外,从图16中也可以发现,映射系数对蜂窝结构平台的应力的提升效果,随冲击速度的增大而增大。

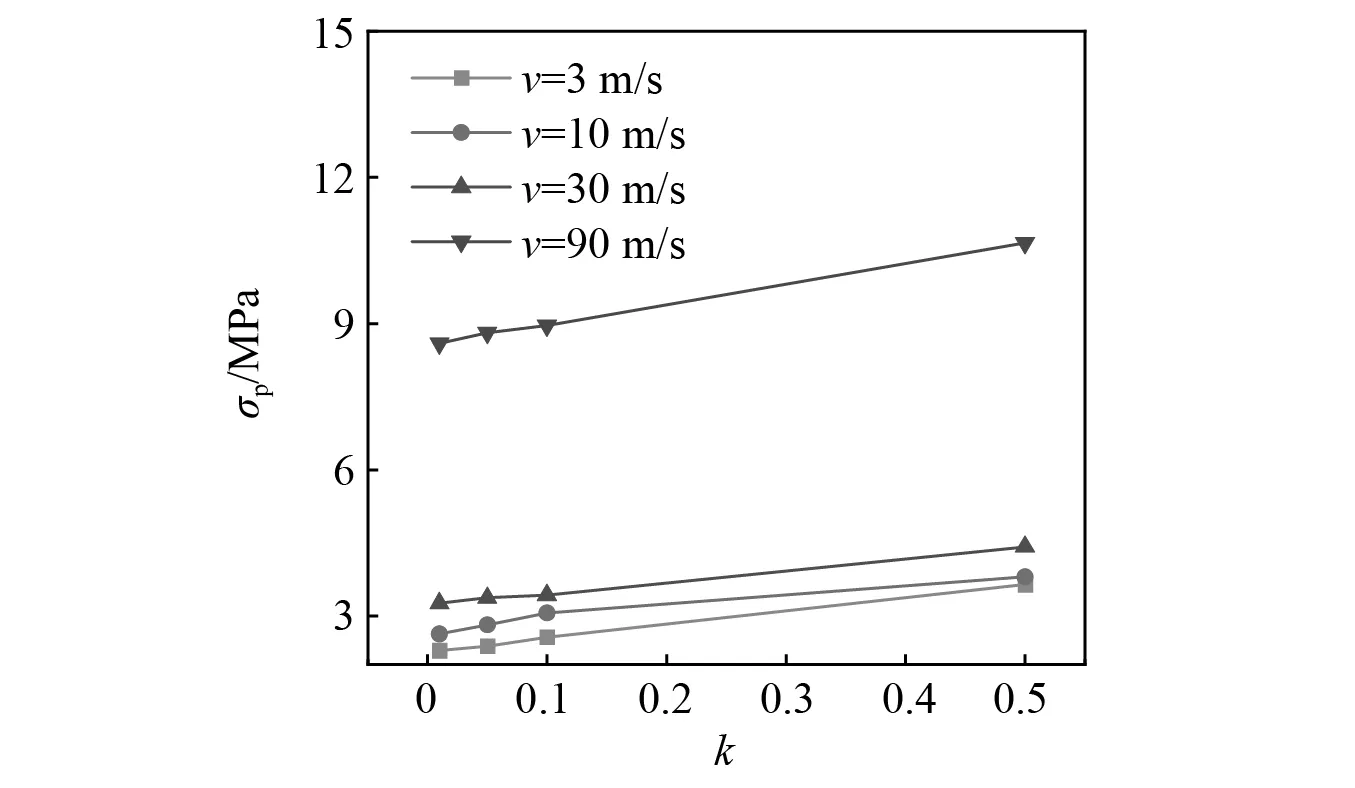
图16 拓扑蜂窝平台应力随映射系数的变化Fig.16 Variation of the platform stress of density mapping honeycomb with the mapping coefficient

具有不同相对密度的拓扑蜂窝的平台应力在不同冲击速度下的应力曲线,如图17所示。由图17可以发现,在相同的冲击速度下,拓扑蜂窝的平台应力随相对密度的增大而增大,这一现象的合理解释是,蜂窝结构整体材料增多,强度增大。且从图17中可以发现,相对密度对拓扑蜂窝结构平台应力的提升效果,随冲击速度的增大而增强。

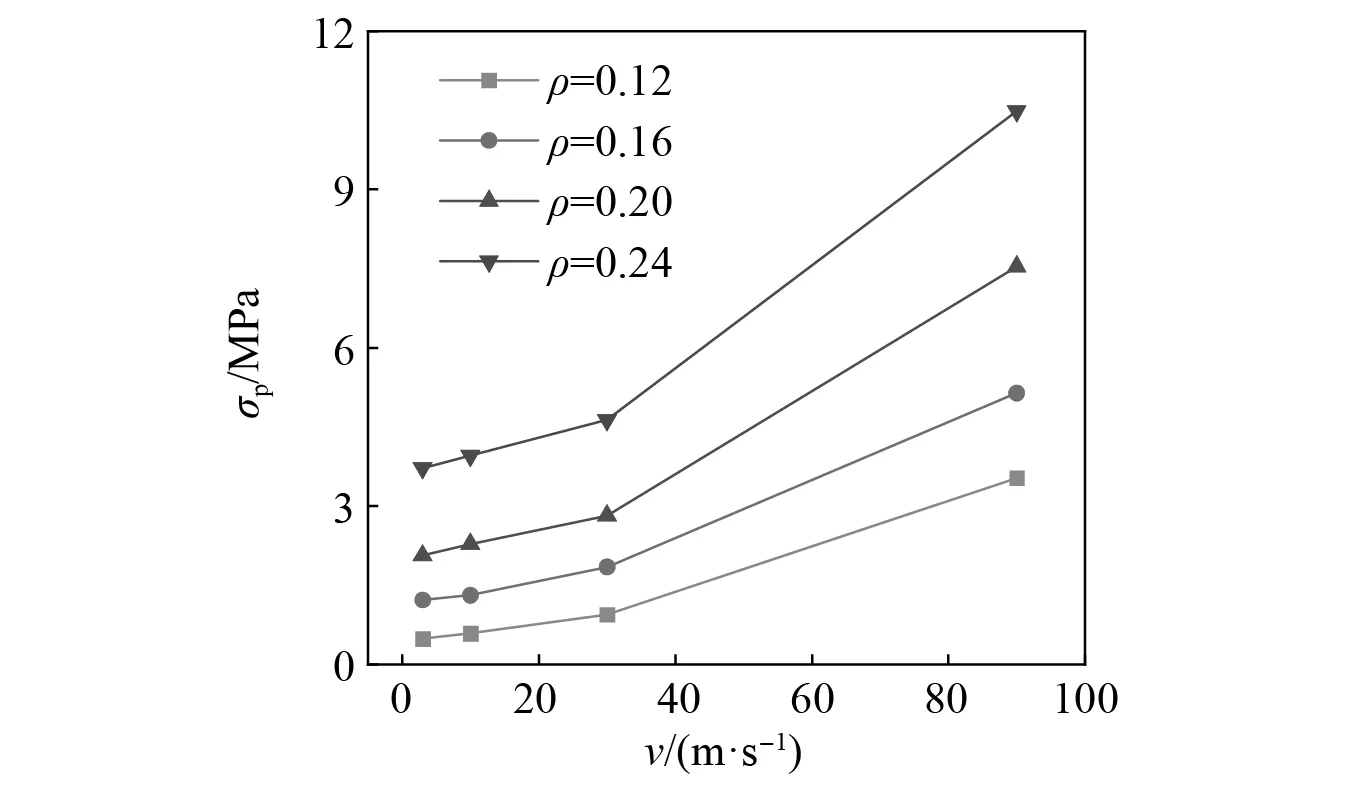
图17 不同相对密度下蜂窝平台应力随冲击速度的变化Fig.17 Variation of honeycomb platform stress with impact velocity under different relative densities

比吸能(specific energy absorption,SEA)是结构碰撞能量吸收的主要评价指标之一,代表了吸能结构单位质量吸收的能量,越大的比吸能表示越优异的能量吸收能力,可定义为

(8)

式中:m为结构总质量;δ为压缩过程中结构的有效位移;x为某时刻的位移;F(x)为冲击时刚性板支反力。

当扑蜂窝的相对密度为0.12时,具有不同映射系数的拓扑蜂窝的比吸能变化曲线,如图18所示。由图18可以发现,在中低速冲击(v=3 m/s,v=10 m/s)下,冲击速度对拓扑蜂窝的比吸能无显著影响,这证明了在低速冲击条件下,冲击速度对拓扑蜂窝比吸能影响较小。此外,在相同冲击速度下,具有不同映射系数的拓扑蜂窝比吸能无明显差异,其中,映射系数较大的拓扑蜂窝在压缩中前段比吸能略高于映射系数较小的拓扑蜂窝,但在拓扑蜂窝接近密实时,具有不同映射系数拓扑蜂窝的比吸能曲线基本相同。

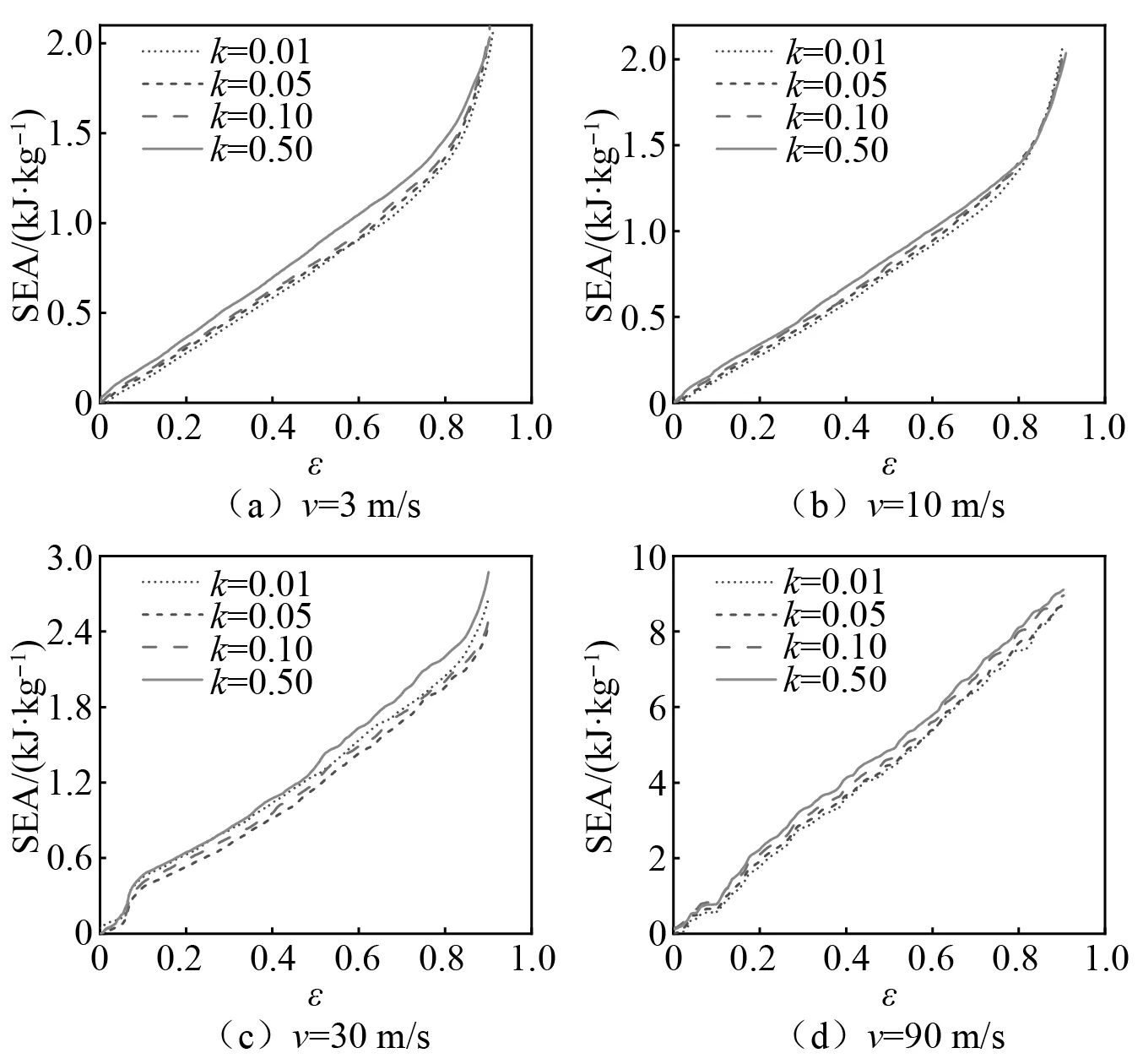
图18 不同拓扑蜂窝的能量吸收特性Fig.18 Energy absorption characteristics of topology optimization honeycombs with different mapping coefficient

当冲击速度进一步增大时,一方面,与传统的均质蜂窝相似,所有非均质蜂窝的能量吸收性能均显著提高,当冲击速度为90 m/s时,蜂窝的最大比吸能甚至达到3 m/s加载速度时的4倍。这主要是由于惯性效应随着冲击速度增加逐渐加强,当位于冲击端的蜂窝被动态载荷加速时,除了外界作用力产生的剪力与弯矩外,位于冲击端的蜂窝自身的惯性也将产生剪力与弯矩,有助于蜂窝结构产生多个塑性铰而充分变形吸能,从而使拓扑蜂窝的比吸能呈现随冲击速度增大而增大的变化趋势。由于惯性效应随冲击速度增大而增大,因此可以合理推断,随着冲击速度进一步增大,惯性效应将进一步增强,蜂窝结构变形更加充分,其比吸能将会被进一步提高。另一方面,拓扑优化对蜂窝比吸能的提升作用开始凸显,如图18(c)和图18(d)所示,映射系数为0.50的拓扑蜂窝的比吸能明显高于其余映射系数较小的拓扑蜂窝。这是由于映射系数直接影响了不同位置的胞元密度权重,此时更大的映射系数可以带来更好的能量吸收性能。但是,映射系数过大也会导致部分蜂窝单元胞壁过薄,从实际生产角度看,应权衡映射系数与胞元壁厚的关系,确保通过拓扑优化方法构造映射密度非均质蜂窝的可行性。

3.4 性能对比研究

为分析将拓扑优化方法引入蜂窝结构对其冲击性能的提升效果,本节构建了与拓扑蜂窝整体结构尺寸相同的标准均质蜂窝,其胞元边长均设置为5 mm。选取k=0.10,ρ=0.12的拓扑蜂窝与标准蜂窝进行对比,冲击速度设置为10 m/s。为保证标准蜂窝与本文提出的拓扑蜂窝质量一致,标准蜂窝的壁厚设置为0.43 mm。研究所采用的面内冲击有限元模型的设置与本文2.2节处保持一致。

为全面对比拓扑蜂窝与标准蜂窝的冲击性能的优劣,且考虑到对比选用的标准蜂窝与拓扑蜂窝的质量相同。因此,选取PCF和SEA作为评价指标。图19所示为标准蜂窝与拓扑蜂窝的冲击性能对比结果。标准蜂窝的PCF为389.6 N,拓扑蜂窝的PCF为323.7 N,下降了16.9%,这主要是由于拓扑蜂窝根据冲击工况将其胞元壁厚进行了连续梯度设置,减小了冲击端胞元壁厚以降低蜂窝结构的PCF;标准蜂窝的SEA为1.65 J/g,拓扑蜂窝的SEA为2.13 J/g,被提高了29.1%。综上,可以得出将拓扑优化方法引入标准蜂窝实现其壁厚的连续梯度设置,相比于标准蜂窝冲击性能上的劣势,拓扑蜂窝有效的降低了初始峰值冲击力,同时提高了其能量吸收性能。