冲击载荷下不同尺寸煤岩动力学分析及损伤特性研究
2023-12-01谢广祥焦振华陈礼鹏
王 磊, 邹 鹏, 谢广祥, 范 浩, 焦振华, 陈礼鹏
(安徽理工大学 深部煤矿采动响应与灾害防控国家重点实验室,安徽 淮南 232001)
深部煤矿开采留设的保护煤柱受冲击地压和爆破震动等高应变率范畴活动影响,势必引起其内部缺陷演化,可能导致煤柱发生破坏失稳[1-4],不利于矿井安全高效开采。冲击载荷下煤柱的破坏与其留设尺寸密切相关[5-6],因此探究不同尺寸煤岩的动力学及损伤特性,对煤矿安全开采及灾害预防具有重要意义。
分离式霍普金森压杆(split Hopkinson pressure bar,SHPB)技术是研究岩石等脆性材料高应变率力学特性的主要方法[7],以此为基础的研究成果颇丰。Li等[8]对花岗岩开展了相同应变速率下的动态压缩试验,得出了试样尺寸与断裂强度的关系。Yuan等[9]研究了冲击载荷下煤岩的尺寸效应,得出应变速率与煤样长度具有相关性。Mishra等[10]对不同长径比岩石开展了冲击压缩试验,探讨了峰值强度、峰值应变和动态弹模对应变率的敏感性。Kao等[11]分别开展了恒定冲击速度和恒定试样尺寸的冲击试验,探究了砂岩应变率效应与尺寸效应之间的关系。吴拥政等[12]研究了三维动静载下不同长径比煤的动力学特性,得出相同应变率下动态峰值应力与长径比的关系。杜晶[13]利用SHPB系统对不同尺寸砂岩进行了冲击试验,得出动态强度随着试样尺寸的变化规律。平琦等[14]研究了高应变率下不同尺寸石灰岩的力学性质,得出动态抗压强度和弹模与试样尺寸的关系。张盛等[15]开展了动态压缩试验,分析了相同直径不同长度砂岩试样的力学特性,得出了动态抗压强度、应变极值和动弹性模量随着试样尺寸的变化规律。李地元等[16]对花岗岩进行了动态加载试验,得出试样长径比变化对动态抗压强度影响较小。
学者们对岩石开展了大量冲击压缩试验,获得动态力学性质的同时也对加载过程中试样的损伤程度进行了探讨。Yin等[17]开展了瓦斯煤岩气固耦合动静组合试验,并基于应力波的传播特征量化了含瓦斯煤的动态损伤。吴帅峰等[18]对花岗岩开展了单轴循环冲击试验,并采用声波测量法表征了损伤参量,得出累积损伤随应变率变化的规律。许金余等[19]开展了岩石的三维冲击试验,采用等效弹模和初始弹模的比值作为损伤度,探讨了损伤度与累积能量吸收值的关系。李夕兵等[20]开展了单轴冲击试验,基于Weibull分布假设研究了混凝土的多次冲击损伤特性,发现损伤-应变曲线呈现出不同形态。穆朝民等[21]通过改进模型建立了体现煤体损伤特征的本构方程,结合数值模拟结果进行了对比分析,研究了冲击载荷下煤的损伤机制。朱晶晶等[22]对砂岩开展了单轴压缩试验,基于Weibull分布的统计损伤理论结合应力-应变曲线,分析了岩石损伤度与应变的变化规律。王登科等[23]对原煤开展了单轴冲击试验,根据岩石力学的强度理论和统计损伤理论,建立了煤的强度型统计损伤本构模型。Zhou等[24]借助SHPB系统发现损伤程度与能量耗散存在相关性,同时基于分形理论讨论了加载后试样的破坏程度。以上研究表明,采用如弹性模量、应力和声波等参量表征动态损伤的方法多用于动静组合或循环冲击条件,且通常具有非连续性,而单轴冲击下试样的损伤多采用理论分析的方法进行描述,手段较为单一研究方法亟需丰富。因此,找寻用以描述岩石动态失稳全过程的连续性损伤指标表征损伤程度显得尤为重要。
鉴于此,本文对不同尺寸煤岩开展单轴冲击试验,探讨受载试样的动力学特性,通过剖析贯穿破坏全过程的能量耗散规律,提出基于能量演化的动态损伤指标K,与基于Weibull分布结合D-P破坏准则表征的损伤变量进行对比,进而验证动态损伤指标K的合理性与适用性。研究结果可为分析和量化冲击全过程中煤岩的损伤程度提供一定参考。
1 试验概况
1.1 试样制备
选用完整且外观无裂隙母岩,经过取芯、切割和打磨等工序,加工成Ф50 mm,长度分别为15 mm,20 mm,25 mm,30 mm,35 mm,40 mm,45 mm和50 mm的试样,并根据ISRM建议确保端面平行度和平面度在0.05 mm及0.02 mm以内,试样如1所示。为降低试验离散性,试验前利用非金属超声波检测仪进行测试,剔除有明显裂隙和波速偏差范围高于10%的试样。
1.2 试验设备
利用SHPB系统对不同尺寸煤样开展了动态压缩试验,系统如图 2所示。其中,入射杆和透射杆长度分别为2 m和1.5 m,杆径均为50 mm,材质为40Cr合金钢,密度为7 800 kg/m3,弹性模量为210 GPa,纵波波速为5 190 m/s。加载过程杆可形成正弦波,实现恒应变率作用。
1.3 试验原理

(1)
式中:A,A0分别为压杆和试样横截面积,m2;E为弹性模量,GPa;C0为纵波波速,m/s;l0为试样初始长度,m。
试验前需对SHPB系统进行标定,以获得可靠的动力学参数。试验过程需保证弹性压杆同心对正,同时在试样两端涂抹凡士林,确保试样与压杆紧密接触。此外,为保证波形具有较为平缓的上升沿,采用异形冲头进行冲击。
1.4 试验方案及结果
对不同尺寸煤样施加了冲击载荷,为控制试验变量的单一性,需保持入射能稳定,试验前进行试冲并选定加载气压为0.35 MPa。本次试验共分8组,每组3个试样,以试样编号MCD-30-1为例进行说明,“MCD”表示不同长度煤样,“30”表示试样长度为30 mm,“1”表示本组试验的第1个试样。
试验的典型波形如图 3所示,可知传播过程中的应力波较为平滑,未出现明显的横向振动,符合一维应力波假设。图 4为煤样的动态应力平衡曲线,入射应力与反射应力之和的曲线与透射应力曲线基本重合,满足应力均匀性假设。试验结果如表1所示。

表1 不同尺寸煤样的力学特性参数Tab.1 Mechanical characteristic parameters of coal samples with different sizes
2 不同尺寸煤样的动态力学特性
2.1 应力-应变曲线特征
图 5为不同尺寸煤样动态压缩应力-应变曲线,根据形态将曲线划分为3个阶段(如图6所示):线弹性阶段(Ⅰ)——曲线直线上升,试样具有明显的脆性,内部应力逐渐趋于平衡;塑性阶段(Ⅱ)——曲线呈上凸形态,斜率逐渐减小,形成不可逆的塑性变形;塑性软化阶段(Ⅲ)——曲线呈下降趋势,试样在峰值应力后迅速变形并失稳,承载能力大大降低。
此外,可以看出曲线形态具有一致性,且表现为“开口型”。分析其原因可能为:试样受到外部冲击后其内部应力快速上升至屈服应力最终达到峰值强度;与此同时,由应力波输入的各种形式能量得以释放,导致试样发生变形,其中出现的不可逆破坏逐渐累积,引发曲线出现“开口型”特征。
2.2 应变率及峰值应力
应变率和峰值应力随试样尺寸变化的关系,分别如图7和图8所示。随着煤样长度的增加,应变率呈现下降趋势,由长度为15 mm时的319.09 s-1下降至长度为50 mm时的106.67 s-1,降低了212.42 s-1。这是因为煤样受到冲击后端面产生形变,从而形成端部应力,长度愈长的试样端部效应更低应力更加分散,故表现出更低的应变率。
峰值应力随着煤样尺寸的增加,由长度为15 mm时的38.58 MPa降低至长度为50 mm时的27.69 MPa,极差为12.42 MPa。相同冲击速度不同尺寸煤样的峰值应力呈现出线性关系,表明峰值应力与尺寸之间存在相关性。峰值强度的变化规律可解释为:单轴冲击作用下,由于惯性作用的存在使得试样侧向近似处于被动围压状态,试样尺寸的减小强化了“围压”作用。另外,尺寸愈大的试样较尺寸小的试样内含有更丰富的缺陷,基本缺陷越多构成缺陷簇的可能性越大,其中的最大缺陷簇所拥有的裂纹尺寸直接决定了试样强度。因此,峰值应力随着试样尺寸的增加表现出降低趋势。
2.3 动态模量
材料在高应变率下抗变形能力可由动态模量表示,即
(2)
式中:E50为岩石动态弹模,GPa;σd50为动态峰值应力值的50%,MPa;εd50为对应的轴向应变值。
动态模量随煤样尺寸变化的关系,如图 9所示。动态弹模随试样尺寸增加,整体表现为线性增加趋势,由15 mm时的3.19 GPa增加到50 mm时的11.58 GPa,说明动态弹模与试样尺寸之间具有较强的关联性,表现出较好的尺寸敏感性。出现上述现象可能的原因是:较低应变率作用下试样未能发生完全破坏,表现为长度愈长的试样抵抗外部变形能力逐渐增强,而长度愈短的试样在相同外部扰动下表现出弱抗干扰性。高应变率作用下尺寸愈小的试样内部微裂纹演化、扩展速度和宽度增加,这势必使微元体弱化导致承载能力下降,随着试样长度增加这种弱化作用逐渐降低,表现出动态弹模逐渐增加。
3 基于能量演化的煤岩动态损伤指标
岩石内部缺陷的发展致使岩石性能劣化从而产生损伤。能量是岩石缺陷扩展和损伤发育的驱动力,因此岩石变形破裂过程必定伴随能量的转化,对岩石变形破裂过程能量演化特性进行分析,寻找与能量演化相关的特征量用以表征岩石损伤是可行的。本文基于上述思想,以冲击载荷下不同尺寸煤岩动态压缩试验为基础,通过分析煤样由完整到破坏全过程的能量演化规律,以寻求合适的损伤量化指标,进而探究冲击全过程中煤的损伤劣化程度。
3.1 能量计算
一维动态压缩试验过程中,杆中独立传播的各应力波携带的能量计算公式为
(3)
式中:WI(t),WR(t)和WT(t)分别为t时刻入射能、反射能、透射能;εI(t),εR(t)和εT(t)分别为t时刻入射应变、反射应变、透射应变;A,E分别为压杆截面面积和弹性模量。
各能量间的关系为
WI=WR+WT+WS
(4)
入射能主要由破碎耗能WFD、破碎动能WK和其他耗散能WO组成,并根据文献[25]的结论,简化后可得
WS=WFD
(5)
耗能密度
(6)
结合上述公式,计算得出不同尺寸煤样的能量参数,如表2所示。

表2 不同尺寸煤样的能量参数
冲击载荷下不同尺寸煤样的入射能和破碎耗能变化规律,如图 10所示。
其中,平均入射能变化范围为75.05~85.56 J,极差为10.51 J,说明固定气压下的入射能在一定范围内可以保持稳定。随煤样尺寸的增加,破碎耗能呈现出线性变化趋势,由31.74 J变为21.75 J。破碎耗能是煤样内部原始裂纹扩展和新裂纹发育的主要能量来源,对动态破碎起决定性作用,也是促使损伤加剧的重要条件。
耗能密度随试样尺寸的变化关系,如图11所示。耗能密度随煤样尺寸增加呈幂函数形式由15 mm时的1.08 J/cm3降至50 mm时的0.22 J/cm3,降低了0.86 J/cm3,说明煤样尺寸的增加引起动态稳定性的减弱。岩石内部随机分布着微观孔隙和裂隙,具有似连续又非完全连续,似破断又非完全破断的性质,试样耗能密度越大,越易加剧内部缺陷发育、扩展,当输入能量超过试样的储能极限时,导致裂隙贯通最终形成宏观破裂面。

图1 试验煤样Fig.1 Test coal sample

图2 SHPB系统Fig.2 SHPB system
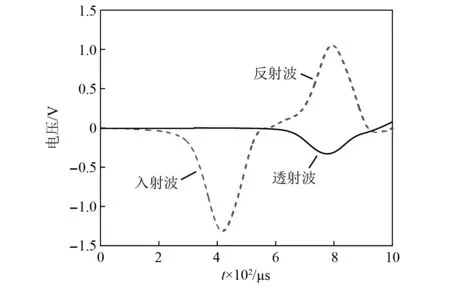
图3 SHPB试验典型波形图Fig.3 Typical waveform of SHPB test

图4 煤样动态应力平衡曲线Fig.4 Dynamic stress equilibrium curve of coal sample
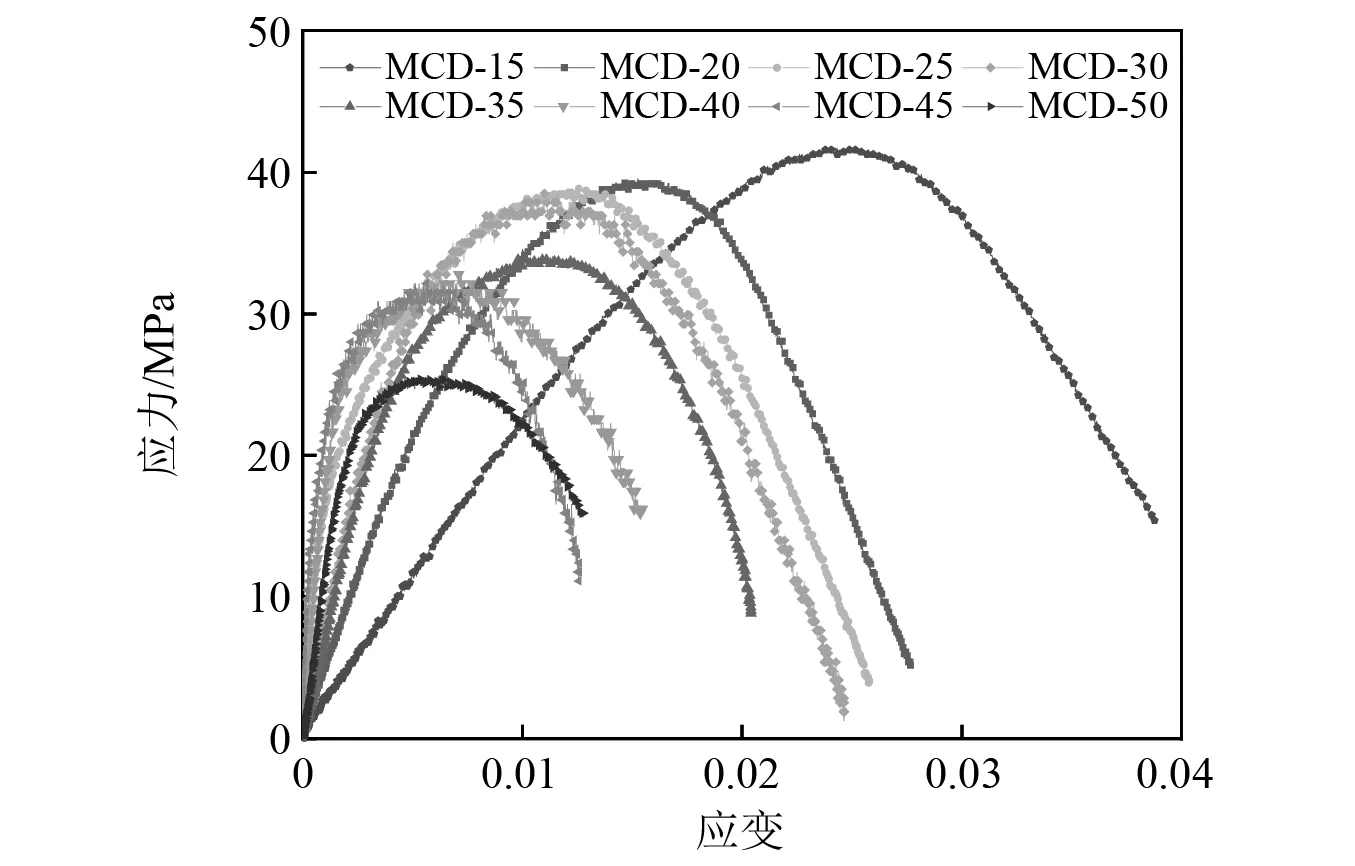
图5 不同尺寸煤样的动态应力-应变曲线Fig.5 Dynamic stress-strain curves of coal samples with different sizes

图6 曲线阶段划分Fig.6 Curve stage division

图7 应变率随尺寸变化关系Fig.7 Relationship between strain rate and size

图8 峰值应力随尺寸变化关系Fig.8 Relationship between peak stress and size

图9 动态弹模随尺寸变化关系Fig.9 Relationship between dynamic elastic modulus and size
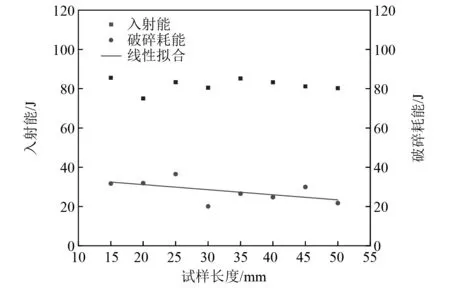
图10 入射能和破碎耗能随尺寸变化关系Fig.10 Relation between incident energy and crushing energy consumption with size
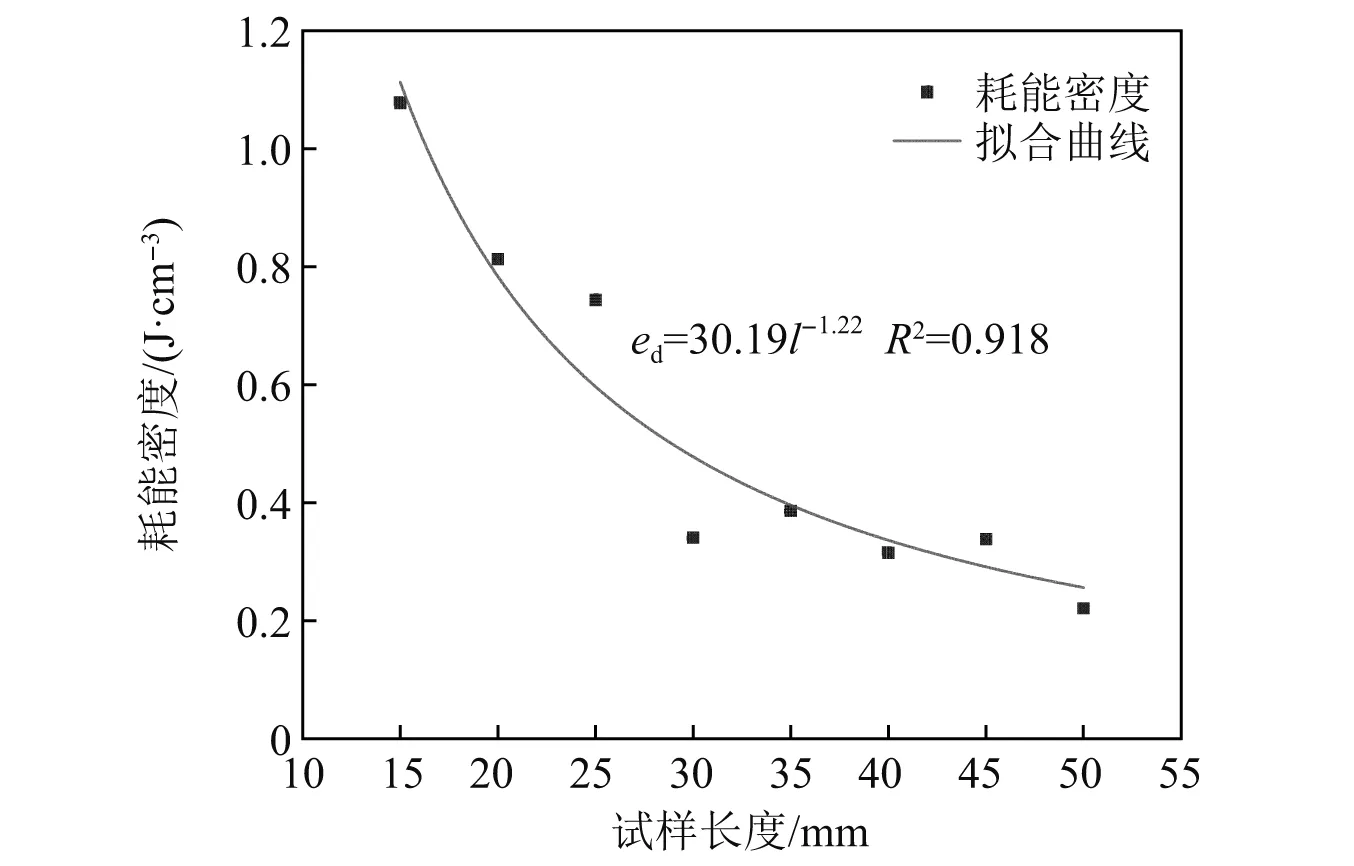
图11 耗能密度随尺寸变化关系Fig.11 Relationship between energy consumption density and coal size

图12 煤岩动态能量演化过程Fig.12 Dynamic energy evolution process of coal rock
为深入剖析受载煤岩破坏过程的能量演化规律,以MCD-15为例并结合应力-应变曲线特征进行分析,结果如图 12所示。
冲击载荷作用下煤岩的入射能、反射能及透射能随着应变的增加呈增长趋势,并在峰后达到最大值。①在弹性阶段(OA)内,入射能和反射能由零开始增长,入射能的增长速率逐渐大于反射能,透射能几乎不变并维持在零点附近,此阶段煤岩吸收的能量主要以弹性能的方式储存;②在塑性阶段(AB)内,入射能和反射能迅速增长,且入射能较反射能的增加速率更明显,透射能开始上升并逐渐增长,此时煤岩内部原生微裂纹扩展的同时产生新的微裂纹;③随着应变的增加,煤岩的应力开始下降,入射能、反射能和透射能均进一步增长,该阶段煤样内部储存的能量得以释放,促使原生裂纹和新生裂纹快速扩展,最终导致煤岩失稳。
3.2 动态损伤指标变化规律
能量演化是导致煤岩损伤劣化的直接因素,通过对上述动态压缩过程中能量的分析,提出动态损伤指标K以探究一维动态压缩全过程煤岩的损伤程度。

(7)
结合式(5)和式(6)可得
(8)
式中:K为动态损伤指标;Wt′,We和WS分别为t′时刻的破碎耗能(t′>te,te为弹性阶段结束时刻)、弹性能和破坏过程t时间内的总破碎耗能,J。
值得注意的是,由能量耗散规律与脆性动态断裂准则可知加载能量存在阈值,当能量值小于此阈值时能量耗散不参与裂纹扩展,试样不产生额外损伤。另外,朱晶晶等认为动态加载弹性阶段试样处于弹性极限内几乎没有损伤。因此,选定上述弹性能为弹性阶段内的能量。
为分析动态损伤指标在试样受载过程中的变化规律,给出其随应变的关系曲线,如图13所示。
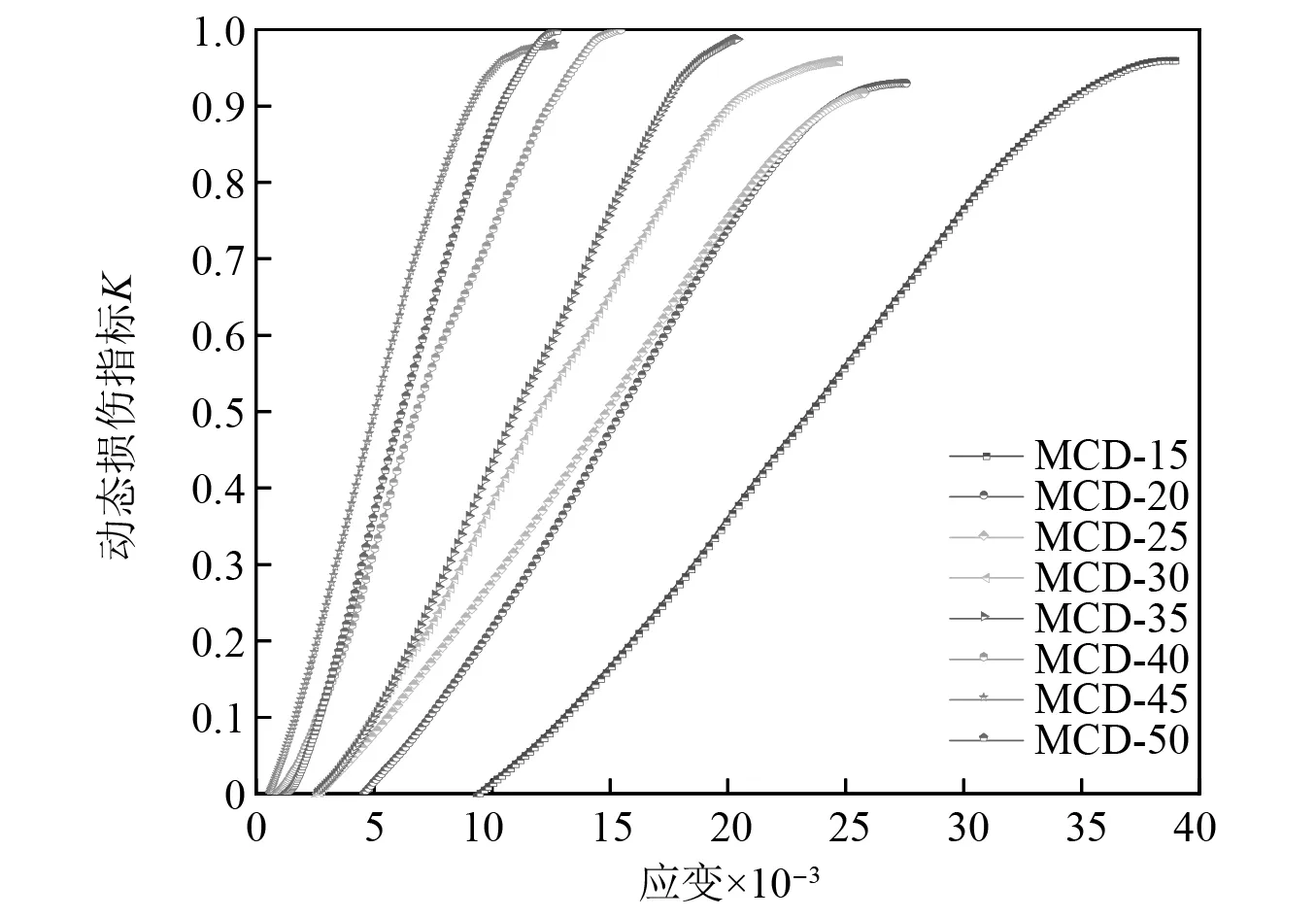
图13 动态损伤指标-应变曲线Fig.13 dynamic damage index-strain curve
由图 13可知,随着轴向应变增大K逐渐增大,曲线形态呈现出相似性。为深入分析K随应变变化规律,参照应力-应变曲线的划分准则,同时选取MCD-15试样为例(如图14所示)对动态损伤指标进行如下分析:冲击载荷作用下不同尺寸煤岩的动态损伤指标在弹性阶段(OA)内弹性能逐渐累积几乎无损伤产生。随着轴向应变的增加,煤样进入塑性阶段(AB),此时试样内部的缺陷在外部能持续输入下开始逐步萌生、发育,内部裂纹朝着不稳定扩展方向发育,K呈近似线性增加,平均变化率为35.98。当应力-应变曲线到达峰值应力时,动态损伤指标出现拐点,由近似线性增大变为缓慢增大,峰后K继续增加并逐渐到达最大损伤位置,此阶段内K的平均变化率为36.97。
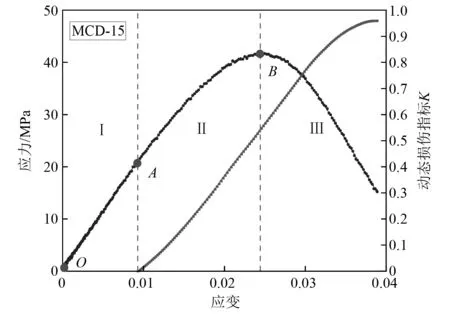
图14 应力/动态损伤指标-应变曲线Fig.14 Stress/dynamic damage index-strain curve
由于煤具有非均质性和非连续性的特性,因此其内部存在着随机分布的微裂纹,煤样受载后激活了微裂纹并使其进一步扩展。加载至弹性阶段结束后微裂纹的局部发生应力集中而起裂,逐渐形成分布裂纹并产生初始损伤,随着应力水平的增加,裂纹逐渐扩展并贯通,损伤进一步加剧。当煤样接近临界状态时,前期形成的分布裂纹加速扩展,裂纹间相互连接最后贯通形成主裂纹。主裂纹形成后将进一步扩展,煤样的裂纹密度迅速增大,直至形成宏观主裂纹,最终导致煤样破坏进而失稳,损伤逐渐接近最大值,反映在应力-应变曲线则为应变持续增加应力逐步降低。
3.3 基于Weibull分布的损伤变量对比验证
以目前使用广泛的基于Weibull分布结合D-P破坏准则表征岩石损伤软化的理论模型,与K进行对比分析,以期说明新指标的合理性及适用性。
煤是一种双重裂隙结构的多孔介质,具有非均质和非连续的特性,因此煤岩内部微缺陷分布无法准确预测。为分析煤的损伤特性,将煤岩视为由多个微元体组成的集合,且微元体具有如下性质:①微元体处于不破坏至破坏的状态满足0~1的分布;②微元体在破坏前满足胡克定律,一旦发生破坏则无法继续承载;③各微元体具有不同强度,但均服从Weibull分布,损伤体的概率密度函数为
(9)
式中:F为微元体强度分布变量;m,F0为Weibull分布参数。
载荷强度的不断增加,导致煤体内部微元体逐渐破坏、缺陷不断萌生发育,为分析煤体的损伤特性,引入基于Weibull分布等假定的损伤变量Dw,即
(10)
式中:Nf为已破坏的微元数目;N为总微元数目。
由于本次为一维动态压缩试验,因此σ2=σ3=0,结合文献[26]的推导过程,利用极值法得出单轴动态压缩下煤岩的损伤变量Dw为
(11)
其中,
(12)
式中,εm为峰值应变。
根据式(12)计算了不同尺寸煤样的损伤变量参数,其结果如表3所示。
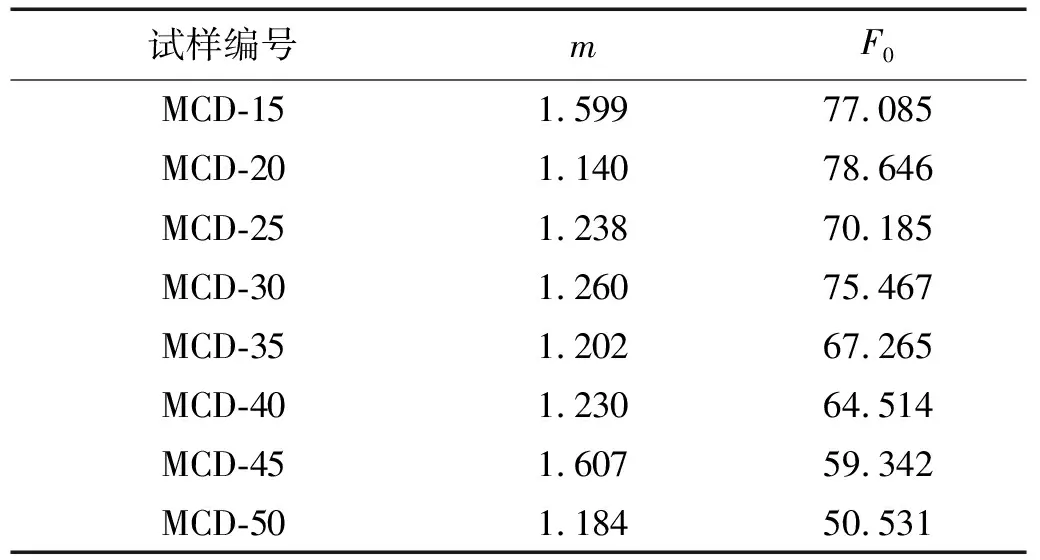
表3 损伤参数计算结果Tab.3 Damage parameter calculation results

表4 煤岩动态损伤指标/损伤变量随应变的变化率
由式(12)可知Dw是ε的函数,即冲击过程中煤岩的损伤变量Dw随着ε的变化发生改变。因此,利用Dw同时结合K对加载全过程的煤岩损伤特性进行综合分析,得到不同尺寸煤岩动态损伤指标K和损伤变量Dw随应变的变化规律如图 15所示。
为对比分析动态损伤指标的变化规律,综合K,Dw变化趋势,以应力-应变曲线各阶段划分为参照,结合图15,给出了动态损伤指标/损伤变量随应变的变化率,如表 4所示。分析可见:①Ⅰ阶段内,随着轴向应变的增加,损伤变量Dw出现增大趋势,平均变化率为49.165,其中MCD-45煤样在此阶段内数值几乎为0,由3.2节可知K在此阶段内无数值;②Ⅱ阶段内,K和Dw曲线形态表现出一致性,变化规律相同且均呈近似线性增长,呈现出较强的规律性,平均变化率分别为60.213和57.609;③Ⅲ阶段内,随轴向变形量的增加,K和Dw曲线形态同样表现出一致性,由近似线性增长变为缓慢增长最终趋于损伤最大值,此阶段内K和Dw的平均变化率分别为52.437和35.800。根据上述曲线特征描述,除在弹性阶段内动态损伤指标主观忽略试样损伤外,其余阶段K和Dw的曲线形态特征呈现良好的相似性,表明动态损伤指标用于表征煤岩损伤程度具有合理性。
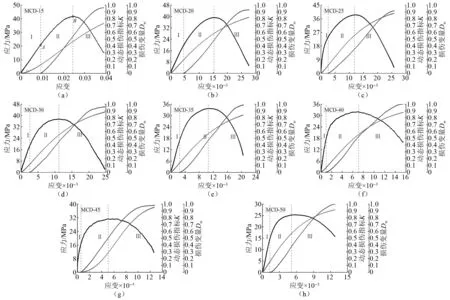
图15 煤岩动态损伤指标/损伤变量-应变曲线Fig.15 Dynamic damage index/damage variable-strain curve of coal rock
整体来看,随着轴向应变的增加,K值在弹性阶段内不表现出损伤,达峰值应力前近似线性增大,峰后指标的增加趋势逐渐平缓;峰值应力前均近似线性增长,峰值应力后增加趋势放缓最终达到损伤变量的最大值。此外,冲击载荷下K和Dw在各阶段内随着煤样尺寸的增加变化率均呈增长趋势,表现出变化率的一致性,结合王磊等[27]研究中分形维数随试样尺寸增大而增大的规律,进一步验证了动态损伤指标的合理性。
值得注意的是,基于Weibull分布结合D-P破坏准则表征的损伤变量,即使使用同一试验材料在不同条件下也可能会得出两种损伤-应变曲线:一种与本文的损伤变量-应变曲线形态相似;另一种则与朱晶晶等的研究类似,此时弹性阶段内损伤度数值几乎为0。这是因为计算损伤时所取的参数与弹性模量、峰值强度和峰值应变等参数有关,因此需结合具体试验方案才能确定最终损伤曲线的形态。然而,通过动态损伤指标表征动态加载过程的试样损伤程度可以在一定程度上避免此类问题的产生,这对分析试样在各加载阶段内的损伤程度具有一定参考。
此外,就最大动态损伤指标和最大损伤变量而言,二者在数值上也存在一定差异。表5给出了利用两种方法计算得出的最大损伤数值,同时绘制图16,通过能量耗散方法得出的最大动态损伤指标与基于Weibull分布结合D-P破坏准则法得出的最大损伤变量相比,标准差更小,表现出更好的稳定性;数值上最大动态损伤指标更接近于1,而最大损伤变量则与微元体强度分布状态极值存在一定差距。因此采用能量耗散的方法表征动态加载全过程中不同尺寸煤岩的损伤特性具有精度更高的特点,也说明此方法具有一定的适用性。

表5 损伤参数极值及标准差
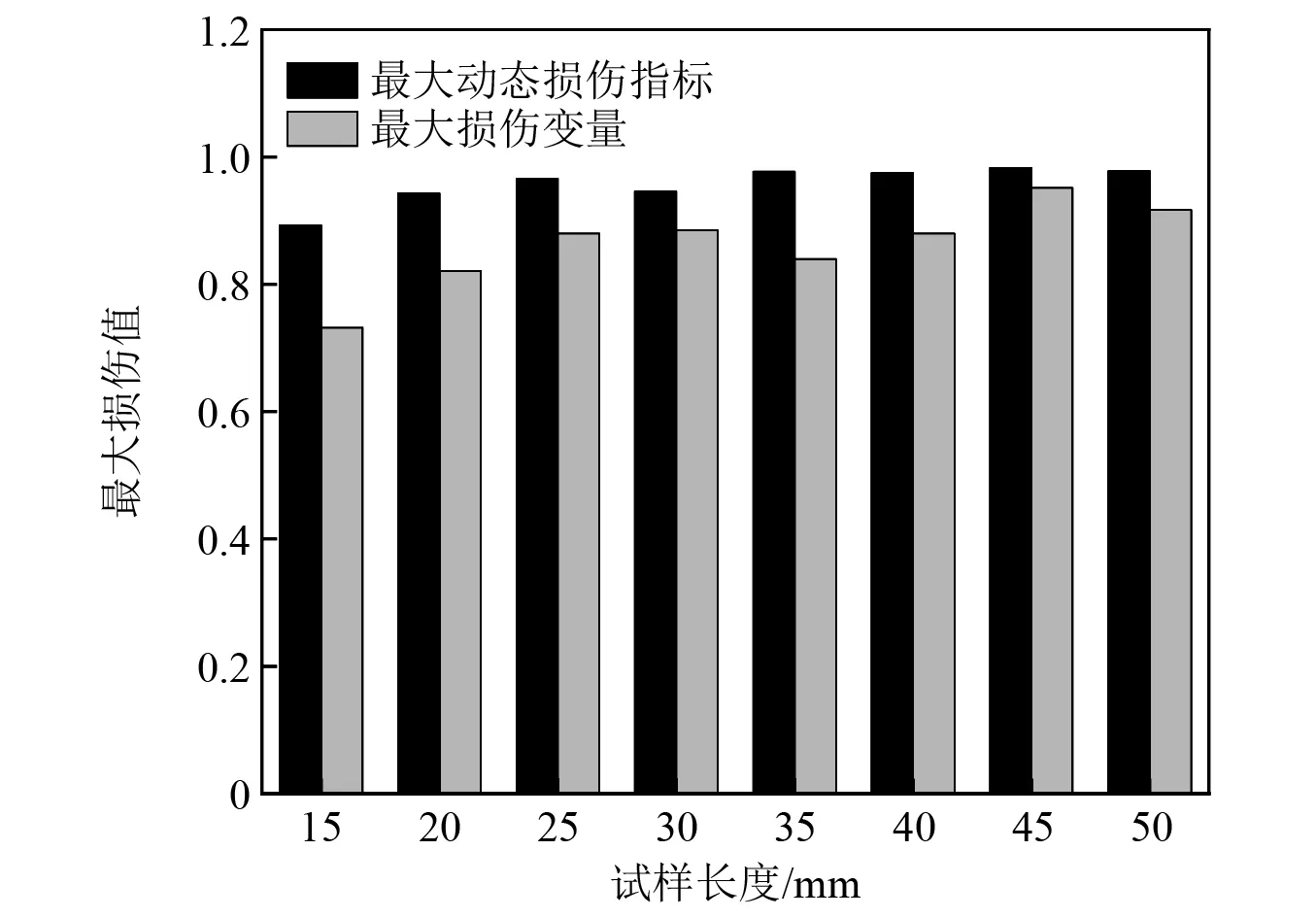
图16 最大损伤值对比Fig.16 Comparison of maximum damage values
4 结 论
本文对相同直径不同高度的煤岩开展了动态压缩试验,探究了冲击载荷作用下煤岩的动力学参数与尺寸的变化关系,通过分析能量演化规律,提出了基于能量耗散的动态损伤指标K,并与基于Weibull分布结合D-P破坏准则表征的损伤变量进行了对比分析,验证了动态损伤指标的合理性与适用性。
(1)不同尺寸煤岩的动态应力-应变曲线可划分为弹性、塑性和塑性软化阶段;应变率和峰值应力与试样尺寸呈线性降低关系,动态模量与试样尺寸呈线性增长关系。
(2)冲击载荷下不同尺寸煤岩的入射能保持稳定、破碎耗能呈线性变化;基于能量耗散规律提出的煤岩动态损伤指标K,具有物理意义明确、计算方便的优点,能够合理反映煤样的损伤程度。
(3)指标K与损伤变量Dw的曲线形态具有相似性,变化趋势具有一致性,表明了K的合理性。指标K的稳定性更高,最大值更接近微元体完全破坏状态,说明了其具有一定的适用性。
