基于音圈电机的柔性杆自抗扰LQR抑振控制算法研究

朱泳廷, 张 泽

(贵州大学 机械工程学院,贵阳 550025)

通过引入柔性结构替换刚性连杆,可以得到轻质的机械臂。相较于传统的刚性机械臂,柔性机械臂具有更好的潜在优势:质量轻、耗能小、驱动器要求低、工作空间大、运转速度快、成本低,以及由于小惯性带来的安全性强等[1]。

柔性会使系统趋于难以控制,一方面由于柔性结构的低刚度特质,机械臂受扰后参数相对于原状态的偏离程度较大;另一方面,非线性特性、低阶模态频率低、阻尼效应弱使得柔性机械臂容易产生振动问题。因此,深入研究并采用各种抑振方法克服柔性机械臂的缺点才能更好发挥其潜在应用优势。

目前对柔性臂的主动抑振方法大致可以分为三类:①将单个柔性臂看作无穷自由度且高度欠驱动(输入量仅有关节力矩)的复杂系统,构造输入量来实现过程抑振[3-6],但抗扰能力较差;②在柔性臂中间部分配置作动应变片和传感器[7-9],这种方法相较于①类方法可为系统引入若干控制量来降低系统欠驱动程度,且根据配置方法等的不同,对特定阶的模态有指向性的、良好的抑制效果,抗扰能力强,缺点则是成本高、控制系统复杂;③配置动力吸振器(dynamic vibration absorber, DVA)在柔性臂的适当位置[10-11],由于吸振器仅配置在固定点,该方法针对较低阶模态且为局部抑振,在吸振器性能限制内可实现较强的抗扰能力。

主动动力吸振技术由于具有频带宽、应用潜力大的优势,在自动化、汽车、船舶、航空航天等工程领域受到重视。Chen等[12]将由智能弹簧构成的主动式动力吸振器置于直升机柔性长桨叶的根部,基于自适应陷波算法实现主动抑振,结果表明该方法能有效地吸收柔性桨叶传递至机身的振动。张洪田等[13]研制了一种电磁式吸振器,采用一种基于改进最小均方算法(modified least mean square,MLMS)的自适应控制器对船舶柴油机进行抑振,仿真验证了主动吸振装置的宽频带抑振效果,但在建模时难以考虑的模型误差和扰动降低了吸振器实际的抑振效果。杨恺等[14]采用一种主动电磁式吸振器对轻质柔性桁架的振动进行抑制,基于Taranti[15]提出的比例系数自适应算法构造控制器,试验表明吸振器对共振和非共振模态振动均有良好的抑制效果,但参数迭代适应的过程较长且抗扰能力较差,不适用于工作条件多变复杂的柔性机械臂。

上述主动抑振方法的一个共同点是均采用一重动力吸振器实现抑振。二重动力吸振器相较于同等质量比的一重动力吸振器对参数变化的适应性更强,而目前采用二重动力吸振器对柔性臂进行主动抑振的研究较少。除此之外,主动式吸振器核心在于作动器的选择。相比于传统的伺服电机,音圈电机结构精简的特点为其带来了体积小、质量轻、动态响应速度快、精度高等优点,广泛应用于高频率、高精度、短距离的重复性运动和定位作业中[16],缺点则是在工作过程中存在参数变化、端部效应等不利因素。采用音圈电机作为作动器有利于减重和提高吸振器性能,但要解决其用于柔性体的振动抑制的控制问题,需要寻求一类低模型依赖的算法。自抗扰控制器(active disturbance rejection controller,ADRC)较前文提到的自适应方法,无参数迭代过程,在解决扰动控制问题上有广泛的应用[17-19]。但需要解决好观测器设计问题,以便系统能够有效的跟踪收敛。

综上所述,本文提出一种由音圈电机构成的主动式二重动力吸振器,阐释基于柔性杆的动力学模型等效建立一阶模态状态方程的方法,分析其扰动形式。控制方法方面采用基于非线性跟踪微分器(non-linear tracking differentiator,NLTD)的线性二次型最优控制(linear quadratic regulator,LQR)方法并结合时变增益扩张状态观测器(time-varing gain extended state observer,VGESO)实现扰动补偿,综合了两种控制方法的优势,使得柔性杆抑振控制不依赖于准确系统模型,且具有强抗扰能力。

1 柔性杆动力学模型

1.1 动力学模型

为了验证抑振算法的效果,以平面单连杆柔性机械臂(planar single-link flexible manipulator,PSLFM)为抑振对象,对柔性杆端部加装吸振器和传感器,实现残余振动的主动抑制。本节基于模态假设法描述柔性杆的振动特性。

一端由关节驱动的PSLFM的结构示意如图1所示,材料、尺寸物理参数在表1中列出。在图1中,θ为该柔性杆对应的关节旋转角度,也是系统主要的输入和激励。对θ进行合适的规划可以有效地降低柔性杆过程中和到位后的残余振动。由于本文不研究θ的规划问题,所以假设柔性杆到位后的残余振动在二重动力吸振器可控的范围内。

表1 柔性杆的物理参数Tab.1 Physical parameters of flexible beam

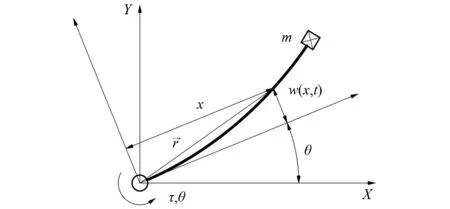
图1 关节驱动PSLFM的结构示意Fig.1 Structure of joint driven PSLFM

设该柔性杆满足Kirchhoff假设,即满足Euler-Bernoulli杆臂条件,条件适用于杆的长度跨距远大于其截面尺寸的情况下。忽略重力的影响,则基于变分原理可推出柔性杆的弯曲无阻尼振动微分方程

(1)

上述四阶偏微分方程的边界条件可通过变分求解过程自然获得,具体推导和结论可参考文献[20]。假设模态法以Rayleigh-Ritz法为基础推导出柔性臂微分方程逼近解,弹性挠度w(x,t)可表达为

(2)

式中:φi(x)为第i阶模态的空间模态函数;pi(t)为第i阶模态的时间模态函数。将式(2)的表达代入式(1)中可得到分离变量的两个独立常微分方程,结合边界条件求解可得解的形式

φi(x)=Ai{aisin(βix)-aisinh(βix)-

cos(βix)+cosh(βix)}

(3)

式中,Ai和ai分别为

(4)

(5)

式中,βi为第i阶空间模态函数φi(x)的特征频率,与时间模态函数pi(t)的固有频率ωi对应,可通过解如下特征方程获得

cos(βiL)cosh(βiL)+1=0

(6)

式(6)是以特征频率βi为变元的方程,其解析解很难得到。端部质量m会影响βi的解,文献[21]探讨了边界条件改变对柔性杆各阶模态的影响规律,指出杆自由端的振幅和振动频率随集中质量m增大的变化,以及末端集中质量m的引入会进一步衰减高阶模态振动,使低阶模态对振动的主导性更强。另一方面,端部质量的增加会降低柔性结构带来的优势,不能仅依靠增加端部质量来抑制高阶模态,因此采用算法对柔性杆高阶模态进行抑制将会更有利于发挥柔性的优势。

考虑关节驱动柔性杆的动力学模型,如图1所示,柔性杆各点在空间中的位置变化是关节旋转与挠度变形的叠加,杆上任意质点的位置可由位矢r表示

(7)

系统的动能为

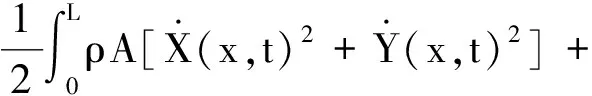
(8)

式中:第一项为柔性杆的总体动能;第二项为末端质量m的动能;第三项为转动动能。忽略重力,系统的弹性势能为

(9)

拉格朗日量取为L=T-U,以关节角度和柔性杆各个时间模态坐标为广义坐标,根据拉格朗日方程

(10)

可获得关节驱动和柔性杆整体的动力学方程

(11)

式中:Mθp为驱动关节与柔性杆的耦合关系;Hp为柔性杆科氏力和离心力作用的体现;Mpp和Kpp为柔性杆作为分布参数系统的质量与刚度性质。

1.2 动力学模型等效参数

本文考虑残余振动问题,即关节角θ=0,式(11)可简化为

(12)

式中,Kpp=diag(k1,k2,…,kn),Mpp可表示为

(13)

式中:第i个主对角元素决定第i阶模态的振动频率;非主对角元素决定了第j阶模态与第i阶模态的耦合效应;ηij的形式为

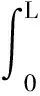
(14)

由于模态的正交性,忽略模态与模态之间的耦合,Mpp主要由主对角元素决定。式(14)的量纲是质量,描述了对应模态的整体振动质量属性。为将该质量属性与实际柔性杆各点的振动效果对应,设l为独立于x的柔性杆位置变量,则可以得到i阶模态在l点处的等效振动质量为

(15)

式(15)决定的振动等效关系可由图2描述,端部第i阶模态的等效振动质量和刚度则可令l=L获得,如下

图2 柔性杆等效质量示意图Fig.2 Representation of equivalent parameters

(16)

(17)

式(15)～式(17)描述了将柔性杆各点的振动等效映射至端点的积分关系,实质上是将式(14)决定的模态空间的参数转换至柔性杆实际物理参数。计算得到的质量和刚度参数有利于二重动力吸振器的建模与控制。

2 基于音圈电机的二重动力吸振器

2.1 音圈电机作动特性

本节对音圈电机的作动特性进行探讨。音圈电机由固定线圈绕组组件和永久磁体组件构成。磁体相对线圈质量较大,将其作为辅助动质量可以增加二重动力吸振器的有效质量比。通电线圈受到动磁体产生的电磁反作用力并传递至固接的抑振对象从而产生抑振效果。

将音圈电机引入被动式无阻尼动力吸振器结构中,系统变为电路、磁力和机械运动系统耦合的复杂模型。音圈电机的电-磁-动力学耦合首要满足以下两个关系

(18)

本文动力吸振器内含的音圈电机作动结构可由图3表示,核心的三个部分分别是音圈电机及编码器组、精密微型导向和轻质吸振器框架。驱动电路系统平衡方程和运动平衡微分方程分别表示为

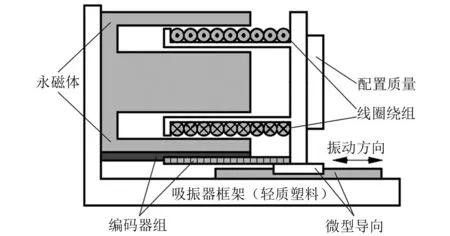
图3 音圈电机作动的结构示意图Fig.3 Structure of voice coil motor actuation

(19)

和

(20)

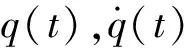
由音圈电机结构上的精简带来的主要问题是磁场的非均匀性,T=T(q)可表示音圈电机的力敏特性曲线。定义驱动电压E(t)=Kcu(t),且定义由自感系数Lm带来的扰动项为ξL,可以得到

(21)

在音圈电机的驱动特性下,动力学模型变为含系统扰动项且阻尼系数和输入增益随位置发生改变的非线性微分方程。设T0为振动系统平衡点处的力敏常数,音圈电机的数学模型可简写为

(22)

由式(21)和式(22)可知,引入音圈电机可为振动系统同时引入磁性阻尼因子c0和可控量u(t)。阻尼系数c0由电路内阻决定上限,可通过调节电阻rf调节。动力吸振器由此不需要额外附加阻尼结构,振动能量的耗散由音圈电机所在电回路实现。

2.2 主动式二重动力吸振器

将音圈电机作动的主动式二重动力吸振器配置至柔性杆端部,如图4所示。

图4 二重动力吸振器端部抑振示意图Fig.4 Representation of end vibration suppression

动力吸振器可基于一般的设计方法,计算满足最优同调条件和最优阻尼条件的动力吸振器最优设计参数。二重动力吸振器工作在最优参数设计下时,其动力学性能与抑振对象的匹配度最高;且相对于一重动力吸振器,对参数变化的敏感性较低。可控量的引入使得动力吸振器在偏离最优参数后仍然有能力保证抑振性能。

考虑以末端一阶模态等效质量、刚度建立振动微分方程,如下

(23)

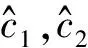
3 自抗扰LQR抑振主动控制方法

3.1 控制目标

基于第2章中对音圈电机作动的二重动力吸振器的探讨,本节建立柔性杆端部抑振的受控模型。引入状态向量和输入向量

(24)

u(t)=[u1(t),u2(t)]T

(25)

柔性杆端部沿弯曲方向的振动微分方程可用状态方程的形式表示

(26)

其中,

式中:A1,A2和B1的具体表达可经由振动微分方程(23)获得;I3为三阶单位阵;ε(t)为系统量测噪声,一般是均值为零的白噪声;ζ(t)中的ξ1和ξ2为音圈电机对应的匹配扰动项,已在式(22)给出其形式;ξw为柔性杆扰动项,主要包括模型误差、残余模态扰动和外扰。

3.2 LQR反馈控制

LQR的控制效果稳定[23],能保证总是以较小的控制量使系统误差趋于零,并且对于多输入多输出系统(multiple-input-multiple-output,MIMO)还可以通过调节权系数来着重保证某一状态量的控制效果。

LQR最优控制方法可描述为使如下的控制性能指标函数最小的问题

(27)

式中:Q的为半正定实对称常矩阵,决定状态量x(t)的权重;R为正定实对称常矩阵,决定对输入控制量u(t)的权重。

为使性能指标函数J(x,u)取得最小值,以达到输入控制量以及状态量的综合最优,定义拉格朗日乘子λ(t)并构建哈密顿函数

λT(t)[Ax(t)+Bu(t)]

(28)

对式(28)求导并令导数为零,可得到最优控制信号为

(29)

式中,P为以下Riccati非线性矩阵方程的解

ATP+PA-PBR-1BTPT+Q=0

(30)

通过求解上述方程可得到矩阵P,由此可得到最优反馈矩阵

K=R-1BTP=[K1,K2]T

(31)

证明:设S为半正定实常值矩阵,并满足如下的等式STS=Q+KTRK,在最优反馈律K的作用下,将状态方程表示为

(32)

式(32)的传递关系可表示为

X(s)=(sI-A+BK)-1ζ(s)

(33)

根据定义,SX(s)的2-范数为

性能指标可改写为

(35)

由Parseval定理可知

(36)

又因输出矩阵C为常值矩阵且扰动ζ(t)有界,当J→minJ(x,u)时

(37)

上述引理表明LQR控制器对噪声(外扰)的抑制能力相对更强,能为其与自抗扰控制器的结合提供良好基础,降低观测器的估计压力。

3.3 自抗扰LQR控制算法

基本的自抗扰控制器主要包括三个核心部分:误差反馈律、NLTD和扩张状态观测器(extend state observer, ESO)。误差反馈律利用误差及误差的微分组合构成最终控制量。NLTD能准确跟踪输入信号以及提取输入信号的微分信号,并同时可作为带宽可调的滤波器实现噪声的滤除。ESO基于非线性函数的良好特性,利用输入量和输出量实时快速地估计系统各阶的状态信息。本节主要引入非线性跟踪微分器NLTD和扩张状态观测器ESO,与3.2节中LQR控制器结合,从而构成自抗扰LQR控制算法。

3.3.1 非线性跟踪微分器NLTD

LQR控制方法须引入状态量及状态量的微分构成误差线性反馈控制律。一种连续形式的NLTD由韩京清[24]提出,如下

(38)

式中:r为加速度跟踪因子;v(t)为输入信号。

考虑式(38)的离散实现,由于二阶积分串联系统的特性,上式决定的离散系统在平衡点附近总是存在“微过调”,系统并不能在有限采样步内完美跟踪输入信号。基于时间最优的等时区法可以得到上式在离散形式下的延拓

(39)

式中,fhan为如下时间最优控制综合函数

(40)

式中:r为加速度跟踪因子;h0为滤波因子;h为采样步长。

式(39)和式(40)即为基于时间最优控制综合函数的非线性TD算法实现。当r足够大,且h0>h时,NLTD可滤除系统的量测噪声。

3.3.2 扩张状态观测器ESO

在一般状态观测器构造方法的基础上,利用非线性函数作为反馈函数,状态观测器误差收敛效率提高,稳态误差得到抑制。定义扩张状态变量为系统的匹配扰动项,则该状态变量能以很高的效率跟随系统的匹配扰动。一种以幂函数作为非线性反馈函数的扩张状态观测器形式如下

(41)

式中:β1～βn+1为非线性函数的增益系数,决定ESO的跟踪性能;f0为系统已知扰动项;状态变量zn+1即为估计得到的“总和扰动”。fal函数的形式为

(42)

由式(42)可知,当跟踪误差|e|>δ时,ESO的反馈估计函数为幂函数形式;而当跟踪误差|e|≤δ时,ESO更接近于线性状态观测器。因此,增大线性区间长度δ将会以降低扰动的估计效率和增大估计稳态误差为代价,使ESO对高频震颤和噪声有更好的抑制作用。

3.3.3 自抗扰LQR抑振控制器设计

为使控制系统具有强鲁棒性以及对内扰、外扰的强补偿能力,本文将自抗扰控制器引入含模型参数误差、含内外扰动的状态方程确定的LQR控制器,结合两者优点,对柔性杆实现基于两个音圈电机的二重动力吸振器的主动抑振控制。

考虑由状态方程式(26)确定的系统,表示为

定义输入量为

(44)

将柔性杆振动简写为

(45)

为了防止ESO的“初始微分峰值”现象造成的冲击对高阶模态产生激励,选择初始时变增益的三阶扩张状态观测器,形式为

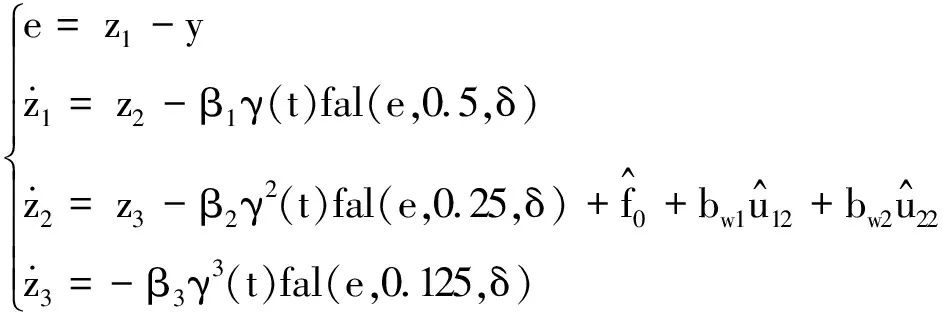
式中,γ(t)为时变增益系数,形式由腾青芳等的研究给出。

(47)

式中:σ为增长速度系数,可调节增益系数增长速度;γ0为增益放大倍率。

(48)

则当ESO的扩张状态量z3能很好地估计总和扰动ξw时,式(23)确定的系统仅由LQR控制器进行调节,音圈电机对应的匹配扰动ξ1和ξ2的影响由LQR控制器的特性而降至最小;并且参数误差、高阶模态响应、音圈电机的输入增益变化等均视作“总和扰动”被补偿。

最终得到的自抗扰LQR控制器如图5所示。

图5 二重动力吸振器抑振自抗扰LQR控制器结构图Fig.5 LQR active disturbance rejection controller structure

4 仿真分析

本文采用MOTICONT公司生产的LCVM-019-016-02型号的小型音圈电机作为二重动力吸振器的作动器,其具体参数如表2所示。

表2 LCVM-019-016-02型号音圈电机的参数Tab.2 Parameters of LCVM-019-016-02 voice coil motor

二重动力吸振器抑振系统的参数如表3所示,柔性杆的前三阶弯曲振动模态的固有频率值如表4所示。

表3 柔性杆、吸振器模型参数Tab.3 Model parameters of flexible beam and DVA

表4 柔性杆前三阶弯曲模态固有频率Tab.4 Natural frequency of the first three bending modes 单位:Hz

对柔性杆二重动力吸振器系统模型实施控制,考察系统抑振能力、参数鲁棒性以及抵抗内外扰的能力,并格外关注控制器对高阶模态扰动的抑制能力。在MATLAB中利用Simulink功能模块搭建自抗扰LQR控制器仿真模型如图6所示。

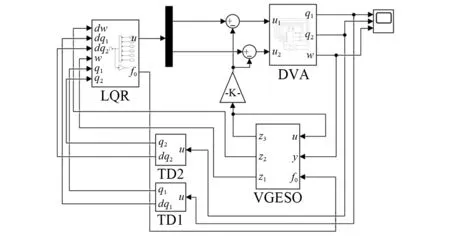
图6 控制器仿真模型Fig.6 Numerical simulation model of controller

图6中的DVA系统模型以2-输入和3-输出的状态方程模型为基础,包含音圈电机力敏常数变化和匹配扰动部分,柔性杆包含外扰和模态扰动部分。

Q=diag(a1,1,1,a2,1,1)

(49)

式中:加权矩阵Q主对角的第一个元素和第四个元素为柔性杆振动速度和振幅的加权系数。文献[25]指出当a1≠a2时,增大振幅权系数有利于抑振效果,但增大速度权系数能更高效地抑制高频的共振峰值。本文着重于控制器的鲁棒性和抗扰能力,系数a1,a2值的选取问题可参阅相关文献。TD,VGESO的仿真参数如表5所示。

表5 TD、VGESO仿真参数Tab.5 Simulation parameters of TD and VGESO

令a1=a2并考察权系数a1,a2分别为1,50和200时的控制器效果,如图7所示。ESO对状态模型中非线性部分扰动观测则如图8所示。

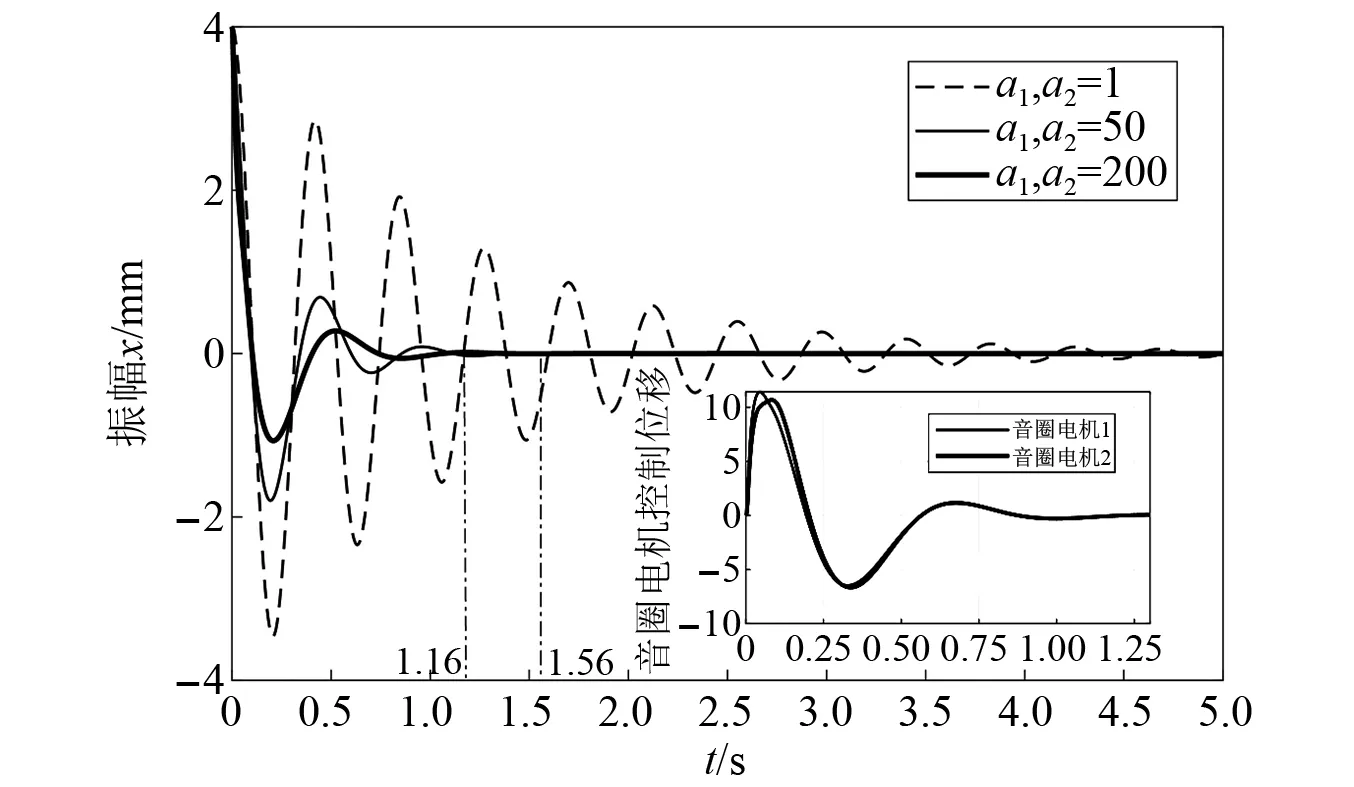
图7 权系数分别为1,50,200时的抑振效果Fig.7 Vibration suppression effect when weighting factors are 1, 50 and 200 respectively

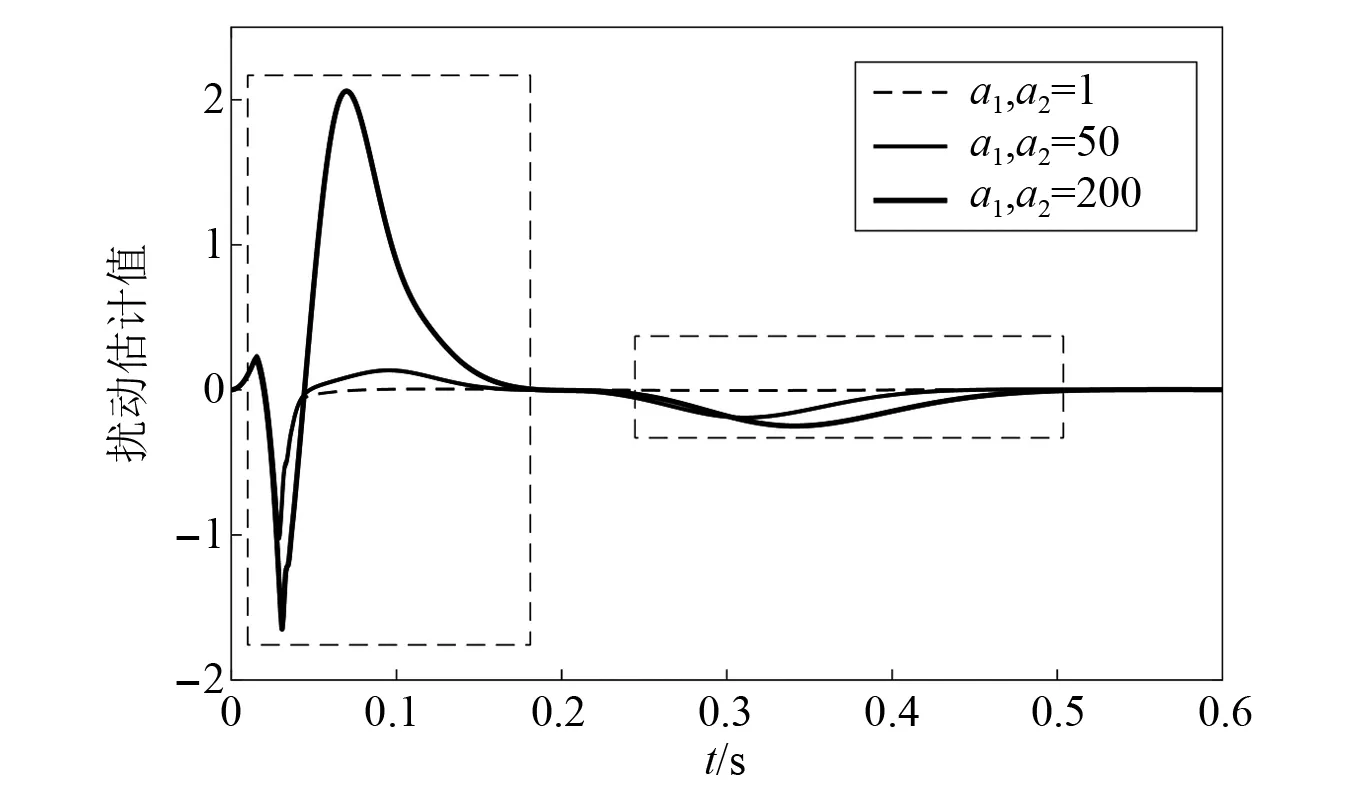
图8 图7对应的ESO扰动估计值Fig.8 ESO estimate corresponding to Fig.7

由图7和图8可知,基于3.3节的控制律设计,引入扰动补偿回路后,LQR控制器和ESO共同发挥了反馈调节功能。LQR控制器主要生成实现抑振的反馈控制信号,而ESO则对LQR控制器误差以及扰动进行补偿,由图8和接下来的仿真结果可体现。

由于吸振器实际物理条件的限制,可通过调节加权系数在条件限制内最大化吸振器的抑振效果,这也是LQR应用于动力吸振器主动控制的优势。对于LQR控制器,增大加权系数对抑振效果的改善十分明显,振动衰减时间分别对应降低到了1.56 s和1.16 s。由图8还可以看到,音圈电机非线性扰动的影响随着权系数的增加而增加,ESO对系统的扰动补偿量增加,此时单一的LQR控制器并不能保证原有的抑振效果。

接下来考察加权系数为200时,各类扰动对系统的影响,包含三种类型的扰动:①模型参数误差;②输入量的摩擦非线性;③高阶模态扰动。

图9和图10分别对比了系统存在模型误差和摩擦死区时的LQR和自抗扰LQR的抑振效果。图9表示等效质量参数偏离+50%(0.5)时,吸振器抑振效果的变化。尽管抑振质量比的下降会使振动抑制效果变差,但LQR控制器的不匹配被ESO实时估计并补偿,控制器的鲁棒性得到提升。图10则表明摩擦非线性对抑振效果的影响,单一的LQR控制器并不能适应吸振器存在摩擦非线性的情况,在摩擦死区的小区间内对应阻尼系数趋于无穷,吸振器失去抑振效果;而引入本文提出的自抗扰LQR控制器后,吸振器可以很好应对摩擦非线性带来的影响。

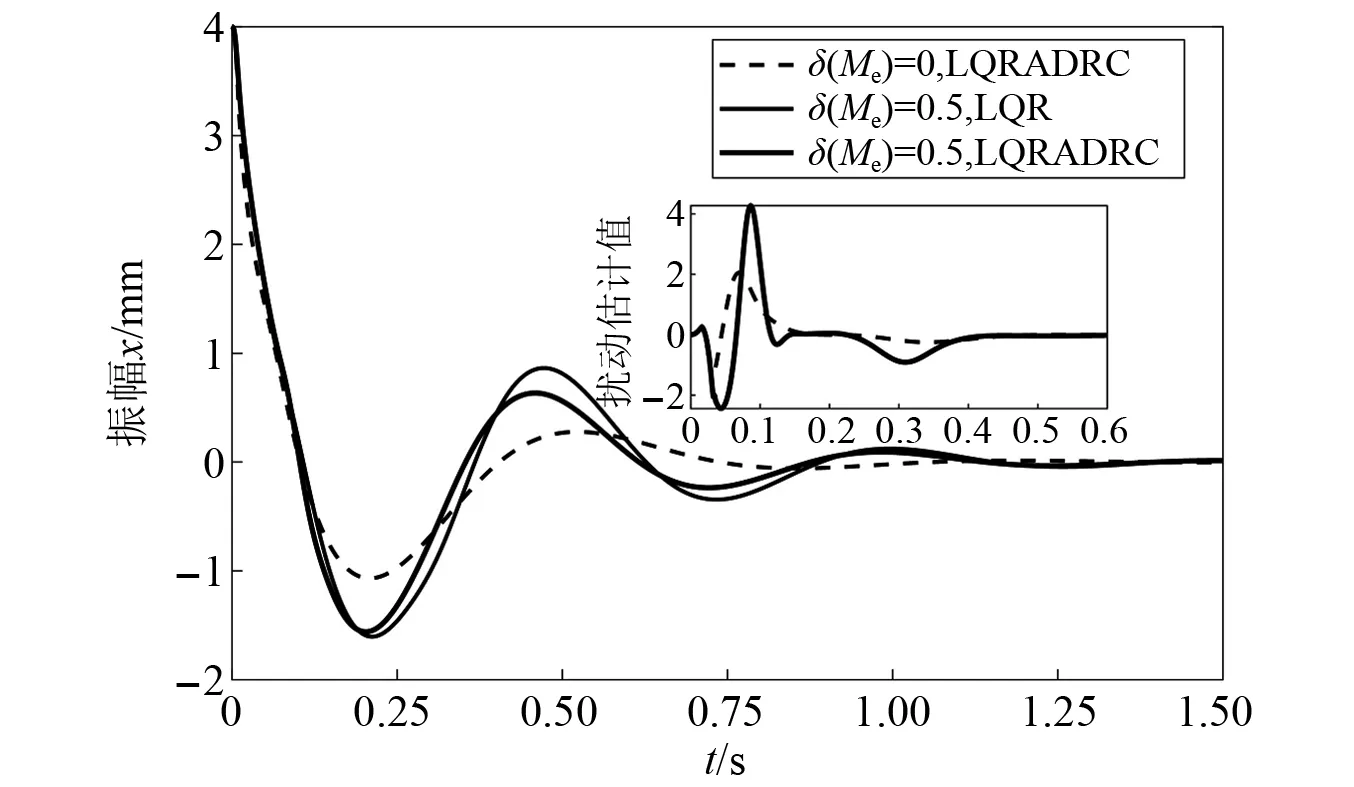
图9 含模型参数误差时的抑振效果Fig.9 Vibration suppression effect with model parameter error

图10 含摩擦非线性时的抑振效果Fig.10 Vibration suppression effect with friction nonlinearity

实际的机械臂工作条件多变且复杂,亦存在可以激发二阶模态之上模态的外界激励。以5sin(105.2t)作为二阶模态扰动,从图11～图13可以考察对比LQR控制器与自抗扰LQR控制器的抑振效果。图11中的两个动质量的振幅与主振动系统的振幅在同一水准,并且两者之间存在有相位差;而图12中的两个动质量的振幅明显增加,柔性杆的振动得到明显抑制,吸振器动质量之一的振幅增加到原本的253%,柔性杆的振动振幅则降低到原来的38.36%。可以看到,二阶模态响应的振动能量很大程度地被吸振器系统吸收,从频域的角度则是增加了二重动力吸振器的抑振带宽。抑振带宽可通过改善观测器的估计性能进一步提高。图13则表明VGESO对实际扰动值有着快速且相对准确的估计效果,并且“初始微分增益”现象也得到抑制。因此,基于该自抗扰LQR控制器的主动式二重动力吸振器对二阶以上模态响应也将有不错的抑制力。

图11 对二阶模态响应的 抑制能力(LQR)Fig.11 Rejection to second-order modal response(LQR)

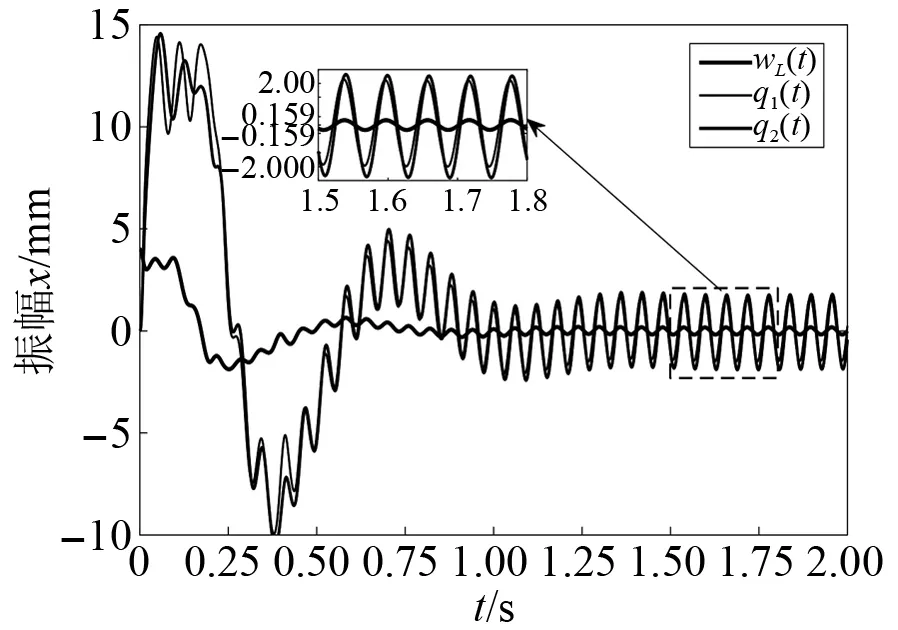
图12 对二阶模态响应的 抑制能力(LQRADRC)Fig.12 Rejection to second-order modal response(LQRADRC)

图13 图12对应的ESO 扰动估计值Fig.13 ESO estimate corresponding to Fig.12

5 结 论

本文利用音圈电机作动的二重动力吸振器对柔性杆端部振动进行抑制,为克服柔性杆本身容易受扰的问题和用于柔性杆抑振的动力吸振器抑振带宽不足的问题,提出将LQR控制器与自抗扰控制器相结合的控制方法。首先,基于柔性杆的动力学模型获得柔性杆的振动等效参数。然后,在分析音圈电机驱动特性和非线性扰动形式的基础上,获得抑振模型的状态方程表达,最终明确了系统特性和扰动因素。利用非线性TD获得LQR控制器所需的原信号和微分信号,引入VGESO并与LQR结合,实现了对模型不确定性、二阶以上模态响应以及未知扰动进行的补偿,达到了良好的抑振效果。该方法对模型参数的准确性要求较低,且兼具有包括抑制模态扰动在内的强抗扰能力,能够有效的提高柔性杆振动主动抑制的鲁棒性和控制精度。