海量数据下光滑分位数回归聚合估计

聂浩巍，李志强

（北京化工大学 数理学院，北京 100029）

0 引言

分位数回归（Quantile Regession，QR）由Koenker 和Basset（t1978）[1]提出，相比于传统的均值回归，分位数回归可以研究不同分位数下协变量对结果的影响，而不需要对误差作出任何假设，因此更加灵活和稳健。从分位数回归被正式提出至今，学者们不断地研究其各种参数估计，并成功将其应用于计量经济学、医学等不同的领域中。

如今，海量数据集常见于各大研究领域，有时数据集甚至以流的形式出现。然而，传统分位数回归需要同时处理整个数据集，而海量数据集由于内存限制很难由单独的一台计算机进行处理。为了解决这个问题，已经开发出了许多基于分治（Divide-and-Conquer，DC）的估计算法。他们大致分为两大类：一类是基于多轮通信的迭代算法，它通过子机器与主机器间多轮信息传输进行迭代以达到处理全数据集的目的[1]，从而快速得到有效的估计量[2—4]。该方法的估计效率较高，但除Chen等（2019）[2]基于核光滑估计方程的迭代算法外，他们均无法处理流数据。另一类是只需要一轮通信（One-shot）的分治算法，首先从各个子数据集中得到局部估计量，然后通过简单平均或加权平均进行聚合，最终得到聚合估计量[5,6]。其中，Lin 和X（i2011）[5]通过展开估计方程得到了一种行之有效的聚合估计算法（Aggregated Estimating Equation Estimation,AEEE），但AEEE要求估计方程可微。然而众所周知，分位数回归的估计方程是不可微的，因此AEEE不能直接用于分位数回归。Chen和Zhou（2020）[6]改进AEEE并成功将其应用于分位数回归中。然而，他们的方法需要通过使用重采样方法获得权重矩阵，这无疑降低了计算速度。因此，有必要开发一种计算效率高且适用于流数据的算法，用于海量数据分位数回归的参数估计。

对此，本文建议使用Fernandes等（2021）[7]提出的光滑方法，将分位数回归的求解问题光滑化，从而满足AEEE中的可微条件，由此提出一种计算高效的海量数据下光滑分位数回归聚合估计（Divide-and-Conquer Smoothing Quantile Regession，DCSQR）算法。具体而言，本文先计算每个数据块的核卷积光滑估计方程估计量和对应的Hessian矩阵，并只需要保留每个数据块的这两个统计信息。若数据是以流的形式接收，则可以不断计算和保存相应统计信息并丢弃原数据集。最后，通过AEEE得到原数据集的有效估计量。本文将通过详细的理论证明给出该估计量的渐近正态性，并通过模拟研究和实证分析证实该方法的有效性。

1.1 光滑分位数回归模型

给定Y∈ℝ 为单变量响应变量，X=(x1，…，xp)T∈ℝp为p维协变量向量,其中x1≡1。假设数据集D={Yi，中含有来自(Y，X)的N个i.i.d.的样本，在给定分位数水平τ∈(0，1)下，本文考虑线性分位数回归模型为：

其中，β0(τ)为关于τ的p维回归参数真值向量，εi满足P[εi≤0|Xi]=τ。为简单起见，下文将省略τ。

分位数回归估计[1]可通过求解如下最小化问题得到：

其中，ρτ(u)=u(τ-I(u＜0)) 是检查损失函数（check loss function），而I(·)是示性函数。根据Buchinsky（1998）[8]的研究，可通过求解以下估计方程来获得β0的经典估计方程估计量

其中，ψτ(u)=τ-I(u＜0)为检查函数。

然而,由于估计方程（3）不可微，因此Lin 和X（i2011）[5]的方法不能推广到分位数回归中。为了避免估计方程的不可微性，本文使用Fernandes等（2021）[7]所提出的核卷积光滑（Kernel Convolution Smoothing）方法，最小化以下光滑分位数回归（Smoothing Quantile Regession，SQR）的目标函数来求解模型（1）中β0的分位数回归估计量

估计问题式（3）转化为求解以下光滑估计方程：

1.2 海量数据下光滑分位数回归聚合估计

当样本量N过大时，由于单台计算机内存有限，直接解决式（6）中的估计方程并不可行，因此本文考虑使用AEEE方法解决上述问题。将数据集D随机分为K块，每块含有n个数据，各块数据集分别记为…，K，其中N=nK，以保证每个块都可以存储在计算机的内存中。对于每块数据集Dk，其对应的光滑估计方程为：

当Rk足够小时，通过简单的推导就可以得到一个式（6）的闭式近似解

1.3 理论性质

A1：参数空间ℬ是Rp的紧子集，参数向量β0是ℬ的内点。

A2：Xki有有界支撑，且Σ0=E[Xi XiT]非奇异。

A3：对于所有0的邻域内的u和几乎所有的x，f(u|x)存在并远离0和∞，且r阶对u连续可微。

A5：窗宽ℎ 满足当n→∞时：（a）Nℎ2r→0 ；（b）Nℎ/lgN→∞。

A6：D0=E[Xi XiTf(0|Xi)]正定且有界。

下面的定理给出了估计量的渐近性质。为了证明定理1，先给出引理1。

利用分部积分公式可得：

对F(-ℎv|Xi)在0处进行r阶泰勒展开，可得：

（b）本文仅证明第一个式子,第二个式子同理。利用分部积分公式，可得：

（c）对F(-ℎv|Xi)在0处进行r阶泰勒展开，可得：

引理1证毕。

定理1：假设条件A1至A4和A5（a）成立，则有：

根据Lindeberg中心极限定理，∀ε＞0，都有：

定理1给出了核卷积光滑估计量的渐近性质。对于各块数据下的局部核卷积光滑估计量，该定理也同样适用。

证明：由条件A2 和A6 可以得到Ak是正定的。根据式（10）可得：

定理2表明，当K以慢于子数据集大小n的速度趋于无穷大时，是β0的相合估计量。

为了证明定理3，先证明引理2。

在β0的η邻域内，对GN(β)使用中值定理：

引理2证毕。

1.4 估计算法

由于SQR具有优良的性质，因此本文可以使用高效的Newton-Raphson 迭代算法来估计，并避免了对讨厌参数的额外估计，从而降低了计算成本。为了进一步降低计算成本，本文选择使用第一块子数据集的标准QR 估计量作为每一块数据的迭代初值。具体算法如下：

步骤1：参数设置：给定窗宽h与核函数K(·)。

步骤2：将数据集D分割成K块,并将各小块数据集Dk分别发送给各子节点。

2 模拟研究

本文使用蒙特卡罗模拟来检验所提出算法在线性模型下的有限样本性能。所有程序都是用Python编写的，并在搭建好的Spark集群上运行，集群包含3 台内存为8G 的计算机，其中一台为主节点，另外两台为子节点。在模拟实证中，统一设置核函数为标准正态分布的概率密度函数最优窗宽的选择可参考Fernandes 等（2021）[7]或He 等（2023）[9]研究中的最小化渐近均方误差（Asymptotic Mean Square Error，AMSE）。由于在模拟研究中结果对窗宽不敏感，因此为简单起见，将窗宽固定为ℎ=1.5N-1/3。

Case 1：同方差正态分布,ϵi～N(0，1)。

Case 2：异方差正态分布,ϵi～N(0，(1+0.1Xi1)2)。

Case 3：指数分布，ϵi～Exp(1)。

因此,对于任何给定的分位数水平τ,给定X的Y的τ条件分位数分别为：

Case 1：同方差正态分布，θ(τ)=θ0+Φ-1(τ)(1，0，0，0，0)T。

Case 2：异方差正态分布，θ(τ)=θ0+Φ-1(τ)(1，0，0，0，0)T+0.1Φ-1(τ)(0，1，0，0，0)T。

Case 3：指数分布，θ(τ)=θ0+Fexp-1(τ)。

其中，Φ和Fexp分别为服从标准正态分布和均值为1的指数分布的向量。

为了证实本文方法的有效性，将总样本量固定为N=1000000，令K在{10，50，100，200，500，1000}内取值，并分别在以上3种不同随机误差下重复模拟实验100次。

本文给出了在分位数水平τ=0.25，0.5，0.75 下，估计量的平均均方误差（Mean Squared Error，MSE）MSE=和计算时间，并将结果与Chen 和Zhou（2020）[6]的算法（Divide-and-Conquer Quantile Regession，DCQR）进行对比，用以证明本文算法的性能。模拟结果基于100次模拟重复实现。

从表1 中可以看到，DCSQR 比DCQR 花费的时间更少，这是因为DCSQR不需要额外估计权重矩阵Ak。这证明了DCSQR在计算速度上的优越性。

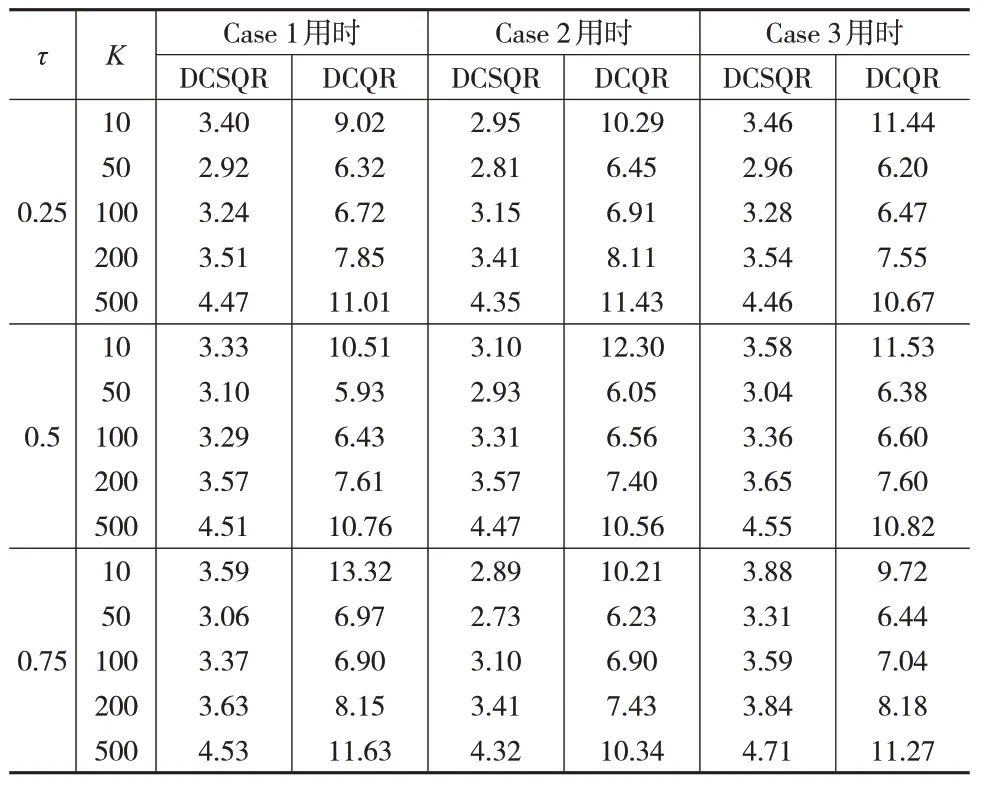
表1 不同环境下DCSQR与DCQR计算时间对比（单位：秒）

而从图1 中可以看出，当K≤200 时，DCSQR 的MSE曲线与DCQR相近且变化幅度更小；当K＞200 时，在多数情况下DCQR 的MSE 小于DCSQR。这说明当K≤200 时DCSQR 的MSE 与DCQR 的稳健性相当。注意到，即使本文模拟研究中使用的分块K的数量超过了定理4 中的理论限制(N=1000000 时分块理论上限K≈31)，DCSQR 在K=200 时也仍然表现良好，当K＞200 以后MSE才快速增大，这意味着关于K的理论条件可以进一步放宽。

3 实证分析

本文将所提出的算法应用于UCI 机器学习存储库报告的温室气体（GHG）观测网络数据集。该数据集由955167 个观测值组成。响应变量是合成观测的GHG 浓度，共有15 个预测因子。这些预测因子是加利福尼亚州14个不同空间区域和加利福尼亚州以外一个区域排放的示踪物的GHG浓度（记为Reg1-Reg15）。

本文先评估了DCSQR 方法的预测精度，并将其与DCQR 方法进行比较。数据集被分为训练数据集和测试数据集，其中训练数据集含有900000个数据，而测试数据集含有55167个数据。然后，本文将训练数据随机分成K块（K∈{5，10，20，50，100，200}），并分别通过DCSQR 和DCQR两种算法来估计回归系数。

表2 给出了两种算法在预测精度和计算成本（总秒数）两个方面的比较结果。从表2中可以看到，DCQR方法较为稳定，当K≤50 时，DCSQR 几乎与DCQR 相当；当K≥100 时DCQR 比DCSQR 稍好，这证明了当K≤50 时DCSQR 的预测稳健性。此外，该表还比较了这两种方法的时间成本。显然，从表2 中可以看到，不论分多少块，DCSQR的用时都要远远小于DCQR的用时。

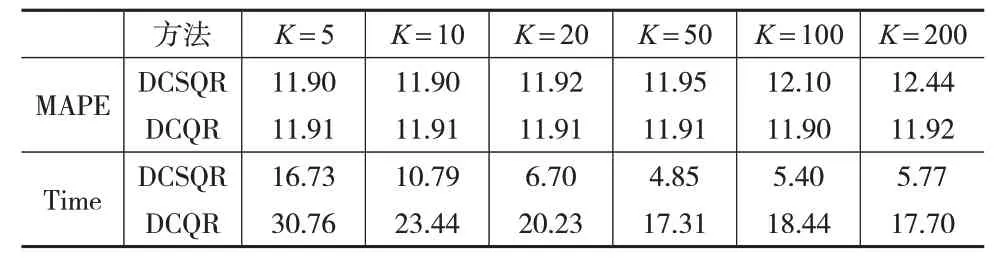
表2 GHG数据集下两种算法的MAPE和计算总秒数对比

4 结论

本文提出了一种基于光滑估计方程的聚合估计算法DCSQR，用于解决海量数据下分位数回归的参数估计问题。理论研究证明，当K以慢于n的一定速度趋于无穷大时，聚合估计量具有和经典分位数回归相同的渐近正态性。模拟实证表明，由于避免了对讨厌参数的估计，DCSQR 算法在保持原有估计精度的基础上，和Chen 和Zhou（2020）[6]基于经典分位数回归的DCQR 算法相比，计算效率显著提高，这证明了DCSQR的有效性。