基于假设检验的区间估计必要样本容量确定
2023-11-30王军虎
王军虎
(洛阳理工学院 经济与管理学院,河南 洛阳 471023)
0 引言
区间估计和假设检验是统计推断的基本内容。用随机样本推断总体数量特征的准确程度一般用抽样误差来表征,抽样误差由登记误差和随机误差组成。登记误差是调查或实验工作的误差,理论上是可以消除的,在推断统计中一般只研究随机误差。随机误差无法消除,但可以通过抽样设计进行控制,其核心是确定必要样本容量。对于单一推断目标的参数闭区间估计的必要样本容量确定方法已经很成熟,林才生和曾五一(2005)[1]、贺建风和刘建平(2008)[2]研究了多推断目标参数估计的必要样本容量确定方法,但研究者很少涉及开区间估计的样本容量,也没有考虑到纳伪错误的概率。郭文(2012)[3]研究了方差假设检验的样本容量,耿修林(2008)[4]研究了方差分析的必要样本容量,但都没有涉及参数估计问题。郑庆玉(2001)[5]单独研究了总体均值闭区间估计与双侧假设检验时必要样本容量的确定方法,但没有建立二者之间的联系。魏杰(2004)[6]对总体均值闭区间估计时的必要样本容量与总体均值左侧假设检验时的必要样本容量进行了简单比较,但未能说明二者之间的本质联系。本文基于抽样推断的基本原理,探索总体参数区间估计与假设检验时必要样本容量的确定方法之间的内在联系,把两类错误纳入闭区间估计和开区间估计的必要样本容量确定之中,以实现对总体参数的科学推断。
1 假设检验必要样本容量的确定
假设检验是利用小概率原理,通过随机样本信息推断事先做出的关于总体某一数量特征的论断是否成立的统计研究方法。假设检验结论的有效性与事先设定的小概率α有关,但并不是越小越好,而是需要同时控制存在着此消彼长关系的两种错误发生的概率,即弃真错误发生的概率α和纳伪错误发生的概率β。通过调节样本容量可以达到有效控制两类错误的目的。
1.1 双侧检验的必要样本容量
总体均值的双侧检验的原假设是“H0:μ=μ0”,备择假设是“H1:μ<μ0或μ>μ0”。
当原假设H0非真而备择假设“H1:μ=μ1(μ1>μ0)”为真时,检验中纳伪错误发生的概率,即:
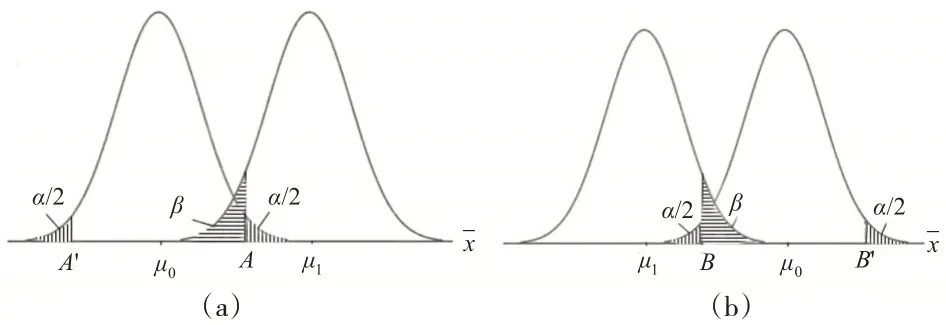
图1 双侧检验中的两类错误图
如图1(b)所示,当原假设“H0:μ=μ0”为真而备择假设“H1:μ=μ1(μ1<μ0)”非真时,检验中弃真错误发生的概率,即公式(1)。
当原假设H0非真而备择假设“H1:μ=μ1(μ1<μ0)”为真时,检验中纳伪错误发生的概率即:
两类错误发生的概率α和β此消彼长。在平衡点B,由公式(1)和公式(5)可以得到:
1.2 单侧检验的必要样本容量
假设x1,x2,…,xn是来自总体X的一个简单随机样本,X~N(μ,σ2),σ2已知,
1.2.1 左侧检验
总体均值左侧检验的原假设是“H0:μ≥μ0”,备择假设是“H1:μ<μ0”。
如图2(a)所示,当原假设“H0:μ=μ0”为真而备择假设“H1:μ<μ0”非真时,检验中弃真错误发生的概率为真),即:
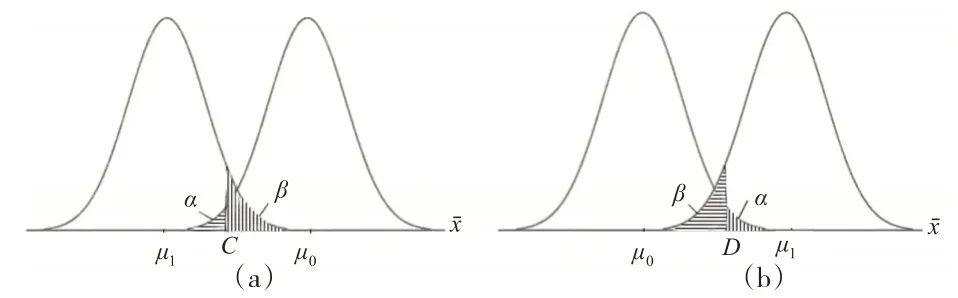
图2 单侧检验中的两类错误图
当原假设H0非真而备择假设“H1:μ=μ1(μ1<μ0)”为真时,检验中纳伪错误发生的概率即公式(5)。在两类错误的平衡点C,由公式(5)和公式(8)可以得到:
1.2.2 右侧检验
总体均值右侧检验的原假设是“H0:μ≤μ0”,备择假设是“H1:μ>μ0”。
如图2(b)所示,当原假设“H0:μ≤μ0”为真而备择假设“H1:μ>μ0”非真时,检验中弃真错误发生的概率为真),即:
在简单随机重复抽样和简单随机不重复抽样下,分别可以推导出与左侧检验相同的兼顾控制两类错误发生的概率α和β的样本容量确定公式(10)和公式(11)。
2 区间估计必要样本容量的确定
参数的区间估计是在给定的置信度1-α下,利用随机样本信息对总体参数真值的取值范围做出的统计推断。评价总体均值μ的区间估计的精度时常用绝对误差来衡量,它是样本均值与总体均值真值的误差。由于总体均值的真值μ是无法得到的,因此估计的绝对误差也无法计算,但在区间估计时需要控制这个绝对误差的取值范围,使它不超过一个极限值Δ,Δ 称为区间估计的极限误差。在区间估计中,置信度1-α和极限误差Δ 呈正向关系。当置信度1-α增大时,区间估计错误的概率α会减小,但极限误差Δ 会增大,估计的精度降低;反之,当提高估计精度时,极限误差Δ 变小,但置信度1-α会降低,区间估计错误的概率α将增大。通过调节样本容量可以有效调和区间估计错误的概率α和极限误差Δ 之间存在的矛盾。
2.1 闭区间估计
总体参数的闭区间估计是指在估计总体参数真值θ时,所估计的1-α置信区间是一个既有上限值又有下限值的闭区间,即为θ的点估计值,Δ ≥0 为估计的极限误差。
2.2 开区间估计
总体参数的开区间估计是指在估计总体参数真值θ时,所估计的1-α置信区间是一个只有上限值或只有下限值的开区间。其中,只有下限值的开区间估计称为最小值开区间估计,即只有上限值的开区间估计称为最大值开区间估计,即
假设x1,x2,…,xn是来自总体X的一个简单随机样本,X~N(μ,σ2),σ2已知,
2.2.1 最小值开区间估计
参照图2(b),在给定的置信度1-α下,有:
2.2.2 最大值开区间估计
参照图2(a),在给定的置信度1-α下,有:
3 假设检验与区间估计两种样本容量确定方法的比较
通过比较总体均值双侧检验的必要样本容量计算公式(4)、公式(7)和总体均值闭区间的必要样本容量计算公式(14)、公式(15),以及总体均值单侧检验的必要样本容量计算公式(10)、公式(11)和总体均值开区间的必要样本容量计算公式(17)、公式(18),可以得到如下结论:
(1)对于单侧检验而言,无论是左侧检验还是右侧检验,确定样本容量都采用同一个计算公式;在进行开区间估计时,无论是最小值开区间估计还是最大值开区间估计,确定样本容量也都采用同一个计算公式。单侧检验和双侧检验、闭区间估计和开区间估计,计算必要样本容量的公式不相同但非常相似。在研究总体均值时,只有一点不同:单侧检验或开区间估计计算必要样本容量公式中的zα在双侧检验或闭区间估计中变成了
(2)假设检验和区间估计的必要样本容量大小与抽样的方式和方法有关,不同的抽样方式和方法下计算必要样本容量的公式是不同的。就简单随机抽样方式而言,采用不重复抽样方法的必要样本容量小于重复抽样方法的必要样本容量。一般而言,分层抽样、系统抽样等其他抽样方式有效地利用了已有的总体信息,降低了随机抽样的盲目性,使样本的代表性增加,可以减小假设检验和区间估计的必要样本容量。
(3)假设检验和区间估计的必要样本容量与总体方差成正比。总体方差越大,总体中的个体变异程度越大,需要抽取更大容量的样本,以保证假设检验中两类错误的概率都得到有效控制或保证区间估计在一定的置信度下的估计精度。反之,总体方差越小,总体中的个体变异程度越低,只需要抽取较小容量的样本就能满足假设检验或区间估计的设计需要。
(4)在计算假设检验的必要样本容量时,需要确定参数真值与其假设值之间的偏差,如|μ1-μ0|。在计算区间估计的必要样本容量时,需要确定参数真值与样本估计值之间允许的最大偏差,如在实践中,|μ1-μ0|和都是未知的,在确定必要样本容量时,可以通过分析增大或减小偏差带来的成本和收益之间的平衡关系来确定这两个离差的最大允许值。两个最大允许偏差值均可以用Δ 来表示。
4 两类错误下的区间估计必要样本容量的确定
作为统计推断的两个基本研究内容,参数的假设检验和区间估计都是依据一个随机样本提供的统计信息和统计量的概率分布原理,在一定的概率保证下,对总体的数量特征进行科学推断。因此,可以用区间估计方法进行假设检验,即在假设检验中用区间估计准则进行检验决策:构造备择假设H1的1-α置信区间,如果备择假设H1的区间完全包含了这个1-α置信区间,那么就拒绝原假设;否则,就接受原假设[7]。用区间估计准则进行假设检验有助于从假设检验的视角认识区间估计问题。
可以把区间估计看作一个假设检验问题。对于单个总体均值的闭区间估计,可以用下列假设检验来表示:
显然,当β=0.5,即zβ=0 时,这样的假设检验的必要样本容量与区间估计的必要样本容量相等。由此可见,参数区间估计的实质是一个忽视纳伪错误的假设检验,它所检验的假设值就是样本估计值。忽视纳伪错误意味着当总体参数的真值没有落入所估计的1-α置信区间时,接受这个置信区间和拒绝这个置信区间具有相同的概率,区间估计方法本身并不能为人们避免接受错误的置信区间提供有用的信息,只能由决策人自己来做出判断。
如果期望区间估计和假设检验一样,能为人们避免接受错误的置信区间提供帮助,那么就不能忽视纳伪错误,必须把纳伪错误发生的概率β和弃真错误发生的概率α同时纳入必要样本容量的确定之中,使两类错误在区间估计中都得到有效控制。
5 两类错误下区间估计的效果模拟
在同时考虑两类错误的条件下进行区间估计时,纳伪错误发生的概率β应控制在0.5以下,zβ>0。此时,进行区间估计的必要样本容量n′大于仅考虑去真错误时进行区间估计的必要样本容量n。由于必要样本容量增大,因此当其他条件不变时,置信区间的宽度变窄,估计的精度提高。下面以简单重复抽样为例,模拟验证在同时考虑两类错误的条件下区间估计必要样本容量的变化及估计精度的变化。
假设总体服从正态分布,且方差σ2已知,采用重复抽样方法从总体中抽取一个简单随机样本。在相同的置信度1-α和相同的极限误差Δ 要求下,控制纳伪错误的概率β与不控制纳伪错误的概率β时,进行区间估计的必要样本容量变化率δn的计算公式分别如下:
抽取的必要样本容量变化后,引起的置信区间宽度变化率δΔ的计算公式分别如下:
当分别取常用的置信度0.90、0.95和0.99时,表1模拟了把纳伪错误的概率β控制在不同水平下的闭区间估计和开区间估计必要样本容量的变化率δn和置信区间宽度的变化率δΔ的变动规律。δn为正值表明控制纳伪错误的概率β之后,必须增加必要样本容量,才能在区间估计中满足同时控制两类错误和极限误差的要求;δΔ为负值表明控制纳伪错误的概率β之后,由于必要样本容量增加,因此区间估计宽度变窄,估计的精度提高。
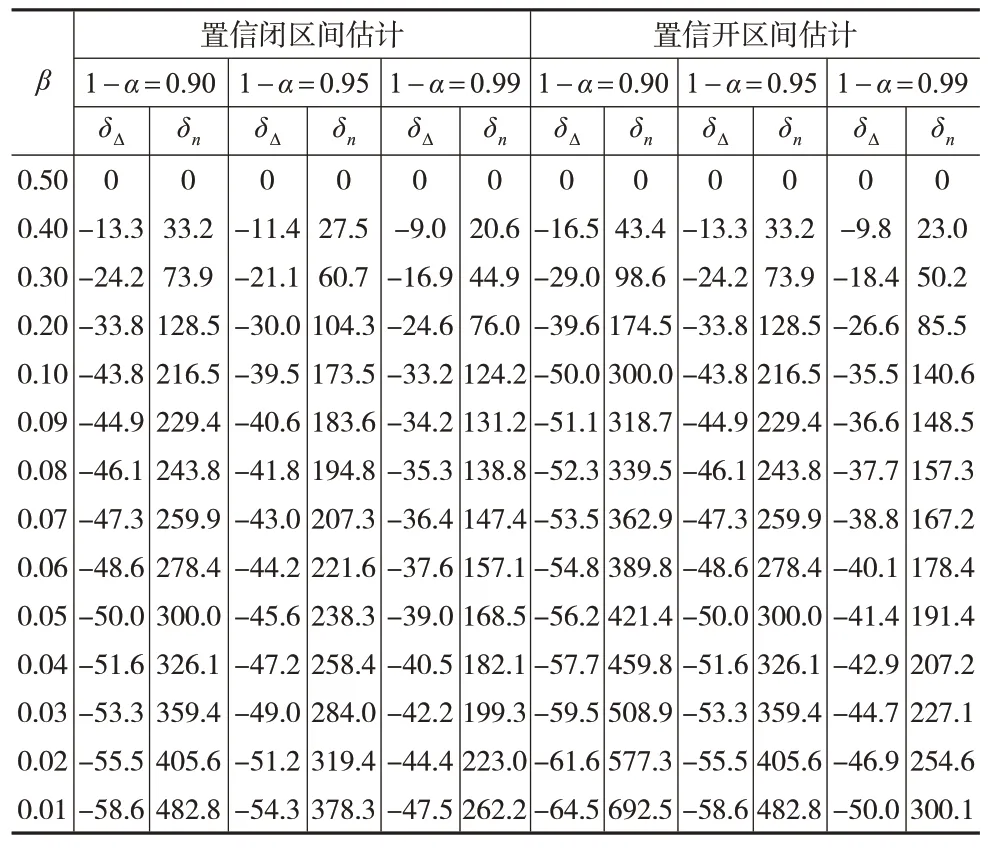
表1 控制两类错误下置信区间宽度变化率和必要样本容量变化率(单位:%)
表1的模拟结果显示,与不考虑纳伪错误的区间估计相比,将纳伪错误的概率β控制得越低,必要样本容量增加得越多,估计结果的精度也越高。在相同的两类错误控制要求下,开区间估计的必要样本容量增加率和估计精度增加率高于闭区间估计。当β取0.20时,必要样本容量约增加1 倍,区间估计的精度约增加30%。当β取0.05 时,必要样本容量约增加1.6至4.2倍,区间估计的精度约增加41%至50%。当β取值减小时,由于必要样本容量增加导致的抽样成本增加的程度可能会大于估计精度增加的程度,因此β的取值不宜太小。
6 结论
本文通过对总体均值单侧检验和双侧检验确定必要样本容量的方法和总体均值开区间估计和闭区间估计确定必要样本容量的方法进行比较,发现二者所依据的数理统计原理相同,主要区别在于二者采用不同的统计方法来推断总体的数量特征。区间估计所提供的方法可以用于进行假设检验。同理,区间估计也可以看作一种特殊的假设检验,即样本统计量计算值是否与总体参数的真值在统计上显著相同。在区间估计中,一般忽略了决策者使用置信区间时可能犯下的纳伪错误的概率为50%。如果决策者希望降低犯纳伪错误的概率,那么就需要在抽样实验设计或抽样调查设计中借助相应的假设检验方法来确定必要的样本容量。当其他条件不变时,在估计置信区间时若要同时控制弃真错误和纳伪错误的概率,则可以通过增加样本容量的方法来实现,进而提高置信区间的精度。
