基于结构匹配性视角的数据质量评估方法

陶春海，钟桂珍

（江西财经大学a.统计学院；b.财经数据科学重点实验室，南昌 330000）

0 引言

数据作为国家各级部门制定相关政策的重要依据，开展数据质量评估方法研究有利于提高数据质量评估的精度，从中把握事物的内在规律，进而提高决策效率。近些年，如何利用科学方法来诊断数据的质量，也成为理论界重点关注和探讨的课题。

关于数据质量评估的研究，从数据质量评估方法来看，主要集中在三个方面：一是利用Benford法则来检测统计数据质量，并构建面板模型进行实证分析[1]；二是基于异常值角度，运用数理统计方法检验数据中的异常值，对离群数据进行显著性检验来评估数据质量[2]；三是在多维统计数据的质量评估中引入Bootstrap统计分布检验法[3]。然而，鲜有学者综合运用三种方法评估数据的质量。从数据质量评估对象来看，现有研究主要关注GDP、GNI[4,5]等指标，但鲜有学者将贫困县调研数据作为研究对象。从数据质量评估视角来看，既有研究要么从数据质量内涵着手，如从精度、准确性、关联性、及时性、一致性等多个维度评估数据质量；要么从误差分析入手，以准确性为着力点，研究数据生产过程中的异常值情况，从而判断数据质量[6]。然而，鲜有学者从结构匹配性视角出发研究数据质量。

综上，既有文献虽为数据质量评估奠定了重要的理论和方法基础[7—10]，但在研究方法、对象和视角上仍存在可拓展的空间。同时，贫困县调研数据刻画了我国贫困地区农户的基本生活现状，对我国全面推进乡村振兴具有重要的理论和现实意义。鉴于此，本文根据贫困县调研数据中家庭成员年龄结构和劳动能力结构与收入之间的匹配性关系，提出基于结构匹配性视角，由Benford 法则、异常值检验、模型一致性和统计分布一致性四个维度共同组成的数据质量综合评估方法，以2020年S省Z贫困县的实地调研数据为样本，验证该方法的有效性，以期为高质量综合评估数据质量提供方法参考。

1 基于结构匹配性视角的数据质量评估方法

1.1 一般性数据质量评估方法

1.1.1 Benford法则数据质量评估方法

Benford法则最早于1881年由美国天文学家和数学家Simon Neweomb发现。经过不断发展和完善，Benford法则在检验数据等方面的应用越来越广泛。基于Benford法则检验数据质量的基本思想是：计算数据集中各位数字的理论频率与实际频率及其差异，构造卡方统计量与临界值比较，验证各位数字是否服从Benford法则。

首位数字（非零非负）按Benford定律出现的频率为：

第二位数字出现的频率为：

……

其中，d1和d2分别表示首位和第二位数字的取值，p(di)表示第i位出现数字di的频率。

由上式计算的首位和第二位数字按Benford法则分布的理论频率见表1。

表1 首位和第二位数字按Benford法则分布的理论频率

卡方检验原假设为理论频率与实际频率无差异，备择假设为理论频率与实际频率存在差异。

构造卡方统计量，χ2统计量的计算公式为：

其中，ei表示第i位数字出现的实际频率，bi表示第i位数字出现的理论频率，N为样本总量。

比较卡方统计量的计算值与临界值。若卡方统计量的计算值小于临界值，则没有理由拒绝原假设，说明理论频率与实际频率无差异，数据遵循Benford 法则。若卡方统计量计算值大于临界值，则拒绝原假设，说明理论频率与实际频率存在差异，数据不符合该法则。

1.1.2 异常值数据质量评估方法

异常值的多少是衡量数据质量的方法之一，同时异常值的存在可能会对分析结果产生较大的负面影响，需要深入研究。通过异常值检验数据质量的原理是：若数据质量好，则数据围绕拟合线分布会比较集中，不会存在大量分布在很远的异常值。

1.1.3 Bootstrap数据质量评估方法

Bootstrap 方法的基本思想是：若初始样本足够大，则根据初始样本生成的一系列Bootstrap 样本计算得到的统计量会无限接近总体的分布，比较原始分布与Bootstrap抽样的统计分布是否一致，从而判断数据质量。

1.2 基于结构匹配性视角的数据质量评估方法

虽然三种方法各有优点和缺点，例如，数据不遵循Benford 法则并不意味着一定存在数据质量问题，但他们的适用范围相对较广，且约束条件较少，故在数据质量评估应用中较为普遍。此外，单一的多元回归、逐步回归和分位数回归模型并不能直接评估数据质量，但考虑到三种回归方法都是统计学的基本方法，应用较广，约束较少，若三个模型的经济学意义和统计学意义一致，则也能够在一定程度上说明数据质量的好坏。

基于此，本文根据一般性数据质量评估方法和相关回归分析理论，提出结构匹配性视角数据质量评估方法：首先，根据Benford 法则初步判断某一核心指标是否服从该法则；其次，异常值的多少不仅影响数据质量，而且可能对建模产生较大的负面影响，故通过异常值检验判断数据质量，并找到异常值的具体位置；然后剔除异常值，再根据数据特征和变量间的匹配性关系分别构建线性和非线性模型，以模型的经济学意义和统计学意义是否一致判断数据质量；最后，根据Bootstrap 抽样方法自助抽样1000 次，检验关键核心指标的均值统计量是否呈对数正态分布，即与原始数据的统计分布是否一致，进而判断数据质量。

1.2.1 基于Benford法则的数据质量检验

基于Benford 法则的数据质量检验的基本思路是：计算数据中某个或某些关键核心指标首位和第二位数字出现的实际频率，比较实际频率与理论频率的差异，并通过卡方检验得到的首位和第二位数字的卡方值是否小于临界值来判断首位和第二位数字是否符合该法则。

1.2.2 基于异常值的数据质量检验

基于异常值的数据质量检验的基本思路是：首先，画出散点图矩阵，初步判断变量之间的关系；其次，通过Q-Q图了解数据分布特征，初步识别异常值的大致位置；最后，利用R 软件中的outlier test 函数，以数据残差值的显著性为依据进行检验，从而找出异常值函数的具体位置和数值。

1.2.3 基于模型一致性的数据质量检验

基于模型一致性的数据质量检验的基本思路是：若数据质量好，则无论线性还是非线性模型，模型的经济学意义和统计学意义都应该保持一致，即数据质量不受模型变化的影响。在剔除异常值的基础上，分别构建多元回归、逐步回归、分位数回归模型，根据各模型参数估计结果的符号（经济学意义）和显著性（统计学意义）是否一致来检验数据质量。

（1）多元回归模型

初步分析数据的分布特征和趋势，厘清解释变量的内在结构和被解释变量之间的匹配性关系。依据相关回归分析理论，构建理论模型如式（4）所示。

式（4）中，Y为被解释变量，X1至Xi为解释变量，ε为随机误差项，β0至βi为回归参数。

（2）逐步回归模型

考虑到多元线性回归模型易受多重共线性问题的影响，进而影响模型的准确性，故选用逐步回归模型筛选合适的变量，避免变量过多等因素导致的模型精度下降，最终形成“最优回归方程”。虽然逐步回归模型在一定程度上改进了传统的线性回归模型，但无法回避的是，逐步回归模型本质上仍然是线性模型，也存在序列相关、异方差等缺陷，需进行经济学和统计学意义检验[13]。

（3）分位数回归模型

仅依靠线性回归模型很难对数据进行全面的质量评估，故需进一步构建非线性回归模型，收入指标常用的非线性回归模型是分位数回归模型。计算公式为：

其中，0 ＜p＜1 表示数值小于第p分位数的比例。在分位数回归模型中，根据垂直距离的加权总和来测量数据点和回归线之间的距离，在拟合线之上数据点的权重为p，否则为1-p。故Y到特定q值的距离为：

若线性模型和非线性模型的参数估计符号一致，即经济学意义一致，统计学意义显著，则可认为解释变量结构和被解释变量具有匹配性关系，数据质量好。

1.2.4 基于Bootstrap自助抽样法的数据质量检验

本文借鉴白永昕等（2020）[3]的做法，对数据质量评估研究的基本思路是：首先判断原始数据是否符合对数正态分布的条件。其次，构建均值统计量，运用Bootstrap 抽样方法从原始数据中抽取1000 次，对均值统计量进行Lilliefor 检验和Anderson-Darling 检验，验证均值统计量是否也遵循对数正态分布规律。若均值统计量通过对数正态分布的检验，则认为Bootstrap机制抽样数据与原数据抽样机制的数据统计分布一致，数据质量较好；反之，则说明数据存在较大误差，需查找误差原因并加以修正，再进行上述检验。最后，人为扩大1 倍原始数据再进行Anderson-Darling检验和Lilliefor检验，若不能通过检测，则说明污染的数据是不能通过检验的。

1.2.5 基于结构匹配性视角的数据质量评估具体方法的递进关系

综上可知，本文提出的基于结构匹配性的数据质量评估方法是从定性和定量两个方面，综合Benford法则、异常值检验、模型一致性、Bootstrap 检验四个维度，从不同方面、角度对数据质量进行评估。具体评估方法之间存在递进关系，因模型一致性需多个指标同时满足三个模型的经济学意义和统计学意义基本一致，所以评估方法的优先原则是模型一致性检验优于Bootstrap检验，Bootstrap检验优于异常值检验和Benford法则检验。

2 实证分析

2.1 贫困县调研数据质量评估的数据来源和基本假设

2.1.1 数据来源

2020 年是我国脱贫攻坚的决胜之年，且新冠肺炎疫情暴发，考虑到深度贫困地区的贫困脆弱性，课题组选取脱贫攻坚主战场之一的S省Z贫困县开展实地调研，深入了解深度贫困地区农户的情况。调研内容涉及农户的家庭成员年龄结构、劳动能力结构、家庭纯收入等，整理获得1193份有效贫困县调研数据。

2.1.2 基本假设

马斯洛需求理论认为，在满足吃、穿、住等最基本的生存需要后，其他需要才会成为新的激励因素，而这些均与收入息息相关。若贫困地区农户的收入高，则基本生存需要不存在问题；若低于某一标准，则基本生存需要存在问题。故贫困地区家庭纯收入的高低与家庭基本生活条件之间的关系是稳定的。基于此，本文提出：

假设1：家庭收入与家庭生活状况具有稳定性。

虽然近些年农村空心化越来越严重，但外出务工人员中很多都是与农村家庭其他成员共享开支。除自然灾害、突发疾病、婚丧嫁娶等因素外，通常情况下家庭人员结构和劳动能力随时间推移遵循生老病死的自然规律，贫困地区家庭成员年龄结构和劳动能力结构具有相对稳定性。基于此，本文提出：

假设2：一定时期内贫困地区家庭成员内部结构具有稳定性。

凯恩斯货币需求理论认为，持有货币受三种动机影响，即交易动机、预防动机、投机动机。基于货币需求理论，贫困地区农户通过家庭成员提供劳动力等要素获得相应收入，来满足日常开支和应对不确定性等因素对家庭的影响。故贫困地区农户的要素贡献与家庭纯收入之间具有结构稳定性。基于此，本文提出：

假设3：要素贡献和家庭纯收入之间具有结构匹配性。

2.2 变量说明

2.2.1 变量定义

被解释变量：家庭纯收入。虽然该指标仅能反映农户的经济状况[9]，但考虑到非收入指标缺乏相对统一的标准，且从1978年开始收入已作为测量我国贫困标准的重要指标，数据又相对容易获得和处理，因此借鉴汪三贵（2018）[10]的做法，选取家庭纯收入作为被解释变量。

解释变量：考虑到家庭成员的年龄结构和劳动能力结构是影响家庭收入的重要因素，本文借鉴已有研究[5,6]的做法，选取家庭常住人口数、义务教育年龄段人数、16～60周岁人数、60周岁及以上人数、患大病人数、残疾人数、患慢性病人数作为解释变量。家庭常住人口数代表家庭人力资本情况，人力资本通过劳动创造家庭纯收入。义务教育年龄段人数能反映家庭潜在的劳动力情况。16～60 周岁人数反映家庭获得家庭纯收入的最大劳动力人数情况。60周岁及以上人数能反映家庭人员结构中需赡养的人员数。患大病人数反映家庭无劳动能力的人数情况。残疾人数和患慢性病人数反映弱劳动力或半劳动力的人数情况。

2.2.2 描述性统计

贫困县调研数据的描述性统计分析结果见表2。

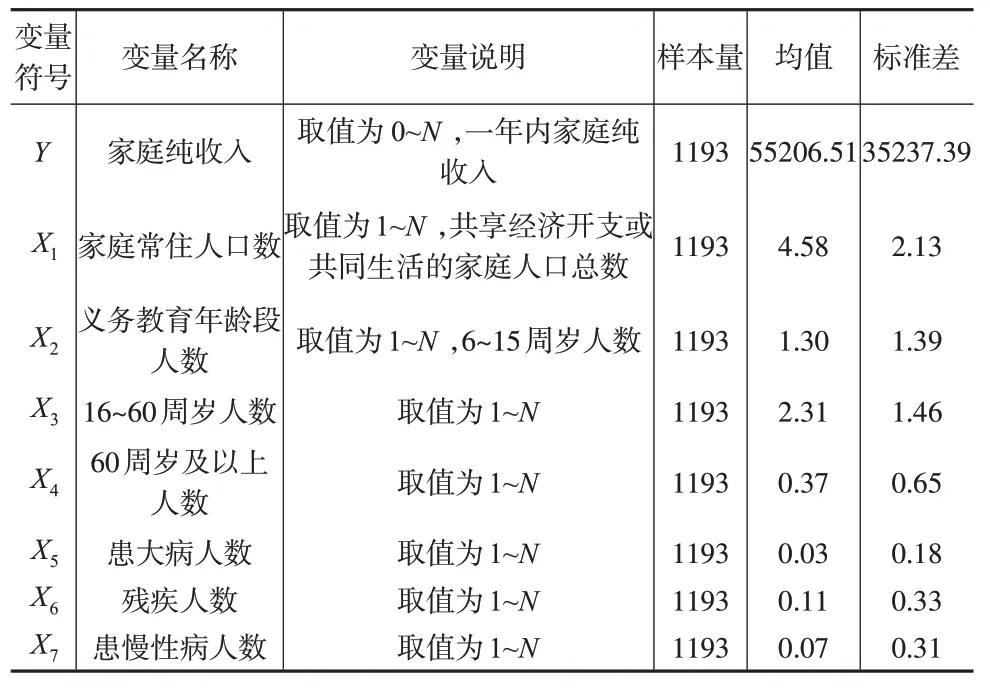
表2 变量说明及描述性统计

从表2 可以看出，S 省Z 贫困县家庭纯收入的均值为55206.51 元，家庭常住人口数的均值约为5 人，结合这两项数据计算可知家庭人均纯收入约为11000余元，高于国家贫困线标准，故贫困县调研数据与我国宣布的消除绝对贫困的结论一致。贫困地区每个家庭义务教育年龄段人数的均值约为1 人，贫困地区家庭16～60 周岁人数的均值约为2人，60周岁及以上人数、患大病人数、残疾人数和患慢性病人数的均值和方差均较小。

2.3 贫困县调研数据质量评估结果

根据前文基于结构匹配性数据质量评估方法的分析，接下来以贫困县调研数据为例，对其进行Benford 法则检验、异常值检验、模型一致性检验、Bootstrap 检验，进而从不同方面、角度评估贫困县调研数据质量，并根据数据质量评估结果验证该方法的有效性。

2.3.1 基于Benford法则的数据质量评估结果

计算家庭纯收入指标首位和第二位数字的实际频率，与根据Benford 法则计算的理论频率进行比较，比较结果见表3。

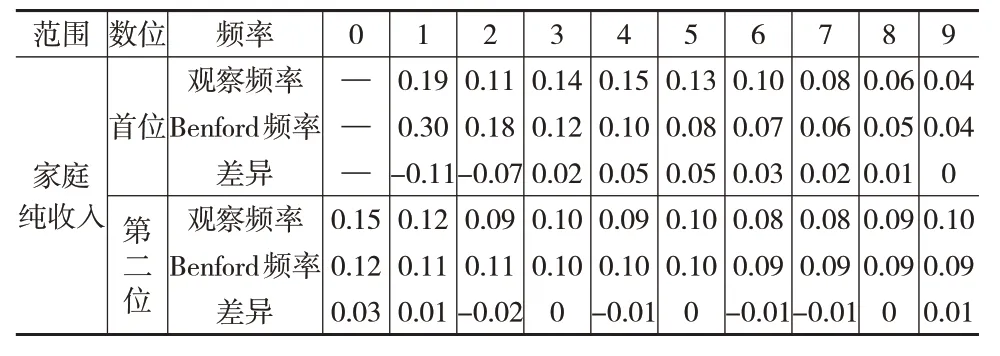
表3 家庭纯收入指标数据的实际频率、理论频率及差异

由表3 可知，除个别数值外，贫困县调研数据的家庭纯收入指标首位数字整体呈现递减趋势，第二位数字呈现波动趋势，但差异的绝对值较小。故需通过卡方拟合优度检验来判断数据是否符合Benford法则。

经计算，首位数字的χ2统计量为174.18，高于临界值15.51，拒绝原假设，说明家庭纯收入首位数字的理论频率和实际频率存在差异。但这并不意味着数据质量存在问题，可能是该法则不适用于贫困县调研数据质量评估，故需进一步采用其他方法综合研判。第二位数字的χ2统计量为16.70，低于临界值16.91，没有足够的理由拒绝原假设，表明该指标的第二位数字符合该法则。这与吴继英和薛艳杰（2021）[1]的研究结果一致。

综上，虽然Benford法则应用范围广泛，但并不意味着该法则能适用于所有数据。故本文将从异常值检验、模型一致性和统计分布一致性三个维度出发综合考量贫困县调研数据家庭成员年龄结构和劳动能力结构与收入之间的匹配性关系，从而验证该方法的有效性。

2.3.2 基于异常值的数据质量评估结果

根据散点图矩阵归纳特征点的分布模式，结果如图1所示。家庭纯收入指标大致呈正态分布，家庭纯收入指标数据随家庭常住人口数、义务教育年龄段人数和16～60周岁人数的增加而增加，家庭纯收入随60周岁及以上人数、患大病人数和残疾人数的增加而下降。

图1 贫困县调研数据变量的散点图矩阵

为进一步分析数据中是否存在异常值，本文构建相应模型进行检验。

由图2 可知，1193 个样本点中仅有3 个离群点，分布在样本中的第848、500 和797 位，故从Q-Q 图来看，贫困县调研数据样本点中离群点较少，贫困县调研数据质量较高。

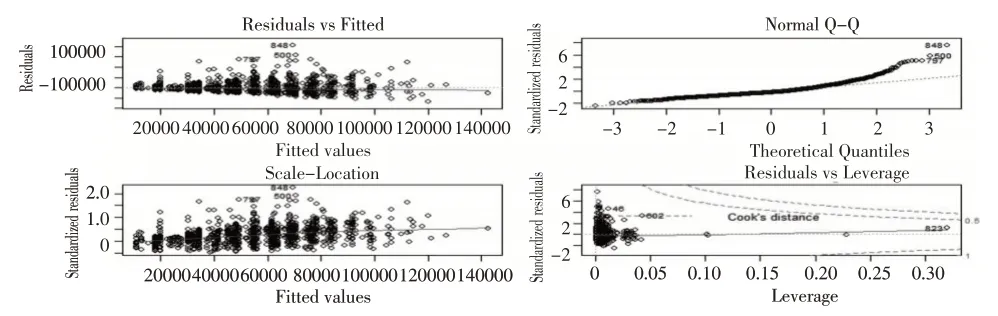
图2 家庭纯收入的Q-Q图

运用R 软件进行outlier test 函数检测发现，在1193 个样本点中检测出10 个离群点，分布在样本的第848、500、797、1028、115、503、501、1031、46 和1020 位，占比不到1%，说明贫困县调研数据质量较高。经分析发现，outlier test函数检测的前3位离群点与Q-Q图中的离群点位置一致，说明这3个必然是离群点。outlier test函数检测出其他7个离群点的P值均小于0.00，残差值显著，因此建模时也需要删除。综合两种方法的检测结果来看，离群点均较少，检测结果具有一致性，说明贫困县调研数据质量较高。

2.3.3 基于模型一致性的数据质量评估结果

根据模型设计，剔除outlier test 函数检测出的10个异常值，运用R软件进行模型参数估计，具体结果见表4。

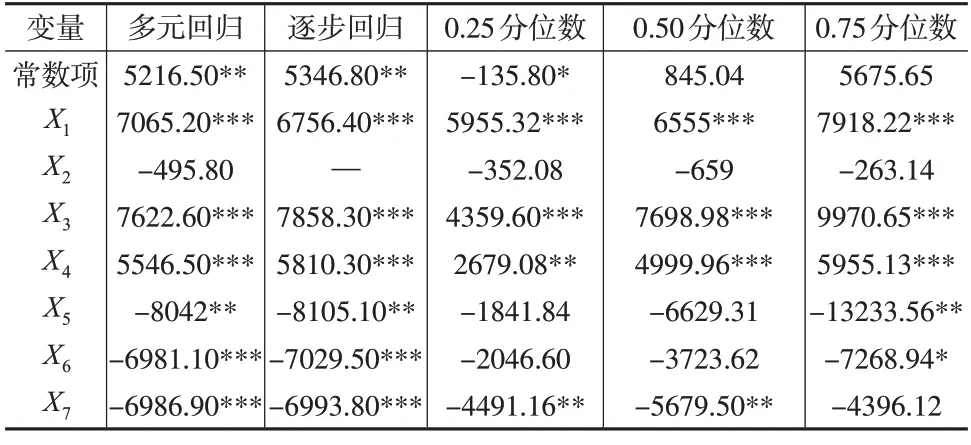
表4 模型一致性参数估计结果

以多元回归模型为例，分析家庭成员年龄结构、劳动能力结构与家庭纯收入指标之间的关系。被解释变量为家庭纯收入，X1为家庭常住人口数，斜率为正，且在1%的水平上显著。当其他变量保持不变时，家庭人数越多，潜在的具备劳动能力的人数也越多，提高家庭纯收入的可能性越大。X2为义务教育年龄段人数，斜率为负，但不显著。在其他变量保持不变的情况下，义务教育年龄段的人数与家庭纯收入之间关系不显著。X3为16～60 周岁人数，斜率为正，且在1%的水平上显著。当其他变量保持不变时，贫困地区农户家庭16～60 周岁人数越多，农户家庭纯收入越高。X4为60 周岁及以上人数，斜率为正，且在1%的水平上显著。当其他变量保持不变时，60 周岁及以上人数越多，家庭纯收入越高，这与人口老龄化会加重家庭负担是不一致的。究其原因，一是贫困地区多是自给自足，家庭养老负担较城市更轻；二是受经济发展水平提升、医疗水平提高等因素影响，劳动力减弱需要一个过程，农村地区60周岁及以上的人仍参加社会生产活动的现象较为普遍，这会增加家庭收入。X5为患大病人数，斜率为负，且在5%的水平上显著。当其他变量保持不变时，家中患大病人数越多，家庭纯收入越少。患大病的劳动力不仅无法获取收入，还需支付大额的看病开销。照顾患大病的人也很难获得收入，家庭整体劳动能力减弱，获取收入的能力下降。X6为残疾人数，斜率为负，且在1%的水平上显著。当其他变量保持不变时，家庭残疾人数越多，家庭纯收入越少。X7为患慢性病人数，斜率为负，且在1%的水平上显著。当其他变量保持不变时，患慢性病如高血压等的人数增加，会使得家庭成员劳动能力减弱，家庭纯收入减少，同时还需支付一定的医疗费用。

从表4的参数估计结果可知，无论是非线性回归模型还是线性回归模型，X1、X3、X4的参数估计结果都显著且参数符号为正，表明家庭常住人口数、16～60周岁人数、60 周岁及以上人数与家庭纯收入存在正向关系。X2、X5、X6、X7的参数估计结果符号为负，且X2不显著，表明义务教育年龄段人数与家庭纯收入的关系不显著，患大病人数、残疾人数和患慢性病人数与家庭纯收入存在负向关系。由此可知，线性和非线性回归模型的参数估计结果具有一致性，从匹配性角度来看，家庭成员年龄结构和劳动能力结构与家庭纯收入是相匹配的，说明贫困县调研数据质量较高。

2.3.4 基于Bootstrap抽样的数据质量评估结果

Cheng 等（2000）[4]已经证明，当统计量反映了总体规模生产、收入等对象时，统计量近似服从对数正态分布。贫困县调研数据中家庭纯收入反映了贫困地区农户的家庭总收入，很容易验证统计量满足规模统计的三个条件，故贫困县调研数据中的家庭纯收入服从对数正态分布。

采用Bootstrap 方法对贫困县调研数据的家庭纯收入指标的数值进行有放回的重复抽样1000 次，得到1000 个Bootstrap样本，计算得到1000个样本均值。为了验证均值统计量是否服从对数正态分布，给出了统计量对数的直方图，如图3所示。

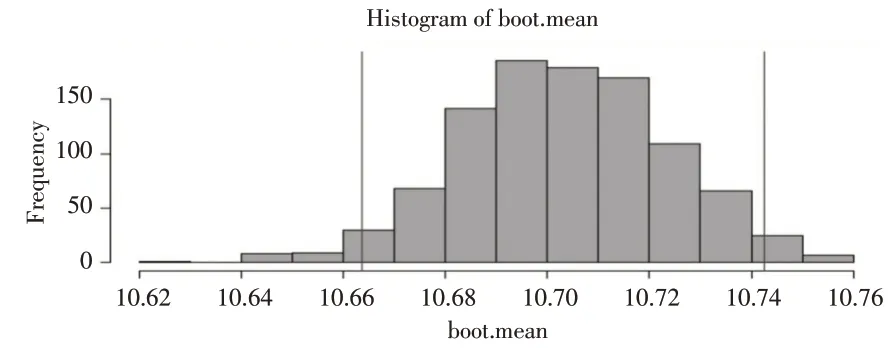
图3 Bootstrap抽样均值统计量分布直方图

根据图3 可知，统计量近似服从对数正态分布。此外，Lilliefor 检验和Anderson-Darling 检验是统计中用来检验数据是否服从正态分布的检验方法，利用上述两种检验方法对统计量的对数进行检验。原假设：数据符合正态分布。备择假设：数据不符合正态分布。经计算，Lilliefor test 检验的D 值为0.02，接近于0，P 值为0.76，明显大于0.05，没有足够的理由拒绝原假设，因此样本数据近似服从对数正态分布。Anderson-Darling 检验结果显示：A 值为0.31，P值为0.55，没有足够的理由拒绝原假设，故Bootstrap抽样数据的样本均值服从对数正态分布。

将原始数据扩大1 倍，即人为增补1193 个数据，再进行Lilliefor 检验和Anderson-Darling 检验，两个检验的P 值分别为2.2e-16和2.2e-6，远小于0.05，说明检验对于伪数据很敏感，即使对原始数据作很小的变动，检验结果也不能通过。综上，本文提出的结构匹配性视角下的数据质量评估方法确实有效。

3 结论与启示

3.1 结论

本文运用系统性思维，从解释变量的结构与被解释变量的匹配性视角出发，提出由Benford 法则、异常值检验、模型一致性和统计分布一致性四个维度共同组成的数据质量综合评估方法。以2020 年S 省Z 贫困县的实地调研数据为样本，从贫困县调研数据中劳动要素结构与收入的匹配性视角出发，应用结构匹配性数据质量评估方法检验贫困县调研数据的质量，从而验证该方法的有效性。

实证研究发现，调研数据中家庭纯收入指标的首位数字不符合Benford法则，第二位数字符合Benford法则，Q-Q图和outlier test 函数检测结果显示，数据样本点中异常值较少，剔除异常值后，多元回归、逐步回归和分位数回归三个模型中的参数估计符号和显著性基本一致，说明劳动要素与收入之间的结构匹配性关系较强，对比Bootstrap机制的模拟抽样数据与真实贫困县调研数据的分布结构可以发现，两套机制收集的数据分布一致，综合来看，调研数据质量较高。

综上，通过实证检验，贫困县调研数据验证了本文提出的结构匹配性视角下的数据质量评估方法确实有效，能从不同方面、角度对数据质量进行评估。

3.2 启示

第一，建立健全现有的数据质量评估体系。在研究对象上，数据质量评估既要关注GDP等宏观性指标，也要关注家庭收入等重要指标；在研究视角上，既要关注准确性、误差最小化等传统视角，也要将结构匹配性视角纳入现有数据质量评估体系中；在数据质量评估方法上，既要关注单一方法的数据质量检验思路，也要注意到联系是普遍的，运用系统性思维，综合运用多种方法检验数据质量的思路是可行的。

第二，拓展结构匹配性视角数据质量评估方法的应用范围。结构匹配性数据质量评估方法不仅能应用于贫困县调研数据，也能应用于其他具有匹配性关系的数据。但是在拓展该方法的应用范围时，要注意各种方法的适用范围和约束条件，找到多种方法融合的可能性，不断优化和改进结构匹配性数据质量评估方法。

第三，加强对匹配性数据质量评估方法的研究。除结构匹配性视角外，理论界还可以从其他维度考虑，以加强对匹配性数据质量评估方法的改进或创新研究。如从空间匹配性视角对基本条件相似的两个地域，就某个或某些指标展开数据质量评估；再如，随着大数据技术的广泛应用，学术界可以从不同数据源的匹配性视角出发，对数据质量展开评估。