函数系数协整模型局部线性估计方法的改进
2023-11-30曹晓舟
曹晓舟
(济南大学 数学科学学院,济南 250002)
0 引言
Cleveland 等(1992)[1]率先研究了函数系数模型,可灵活捕获丰富的动态特征,同时避免完全非参数形式中的“维数困难”现象。随后该模型被广泛用于协整关系的建模,统称为函数系数协整模型。20世纪初,该模型的研究重点是系数的逐点估计方法。方法多基于最小二乘估计构建,此类方法在残差服从正态分布时存在一些良好的性质[2]。同时,Cai 等(2000)[3]使用两步法对系数进行了局部多项式估计;Sun和L(i2011)[4]研究了局部常数和局部线性核估计量,且后者具有更小的均方误差。
随后学者们关注到数据中的异常值,研究发现基于最小绝对离差估计准则(即L1损失函数)构建的局部估计量效果更好[5,6]。同样,模型中同方差的设定在解决现实问题时存在很大局限。部分学者假设动态波动中的主要特征由时变因素引起。Xu和Phillips(2008)[7]、Tu和Wang(2020)[8]分别在研究自回归模型和函数系数协整模型时均提出构建自适应估计流程来减少时变波动方差对估计量产生的偏差;Zhu(2018)[9]扩展研究了含厚尾特征和时变波动的自回归模型,提出自适应最小绝对离差估计量(Adaptive Least Absolute Deviations Estimator,ALADE)。
本文将关注时间序列含厚尾特征及时变波动方差时函数系数协整模型估计流程的优化问题。
1 局部线性ALADE
1.1 引入模型
不失一般性,构建含厚尾特征和时变波动方差的函数系数协整模型(FCCM):
其中,xi,t是单位根过程,其系数依赖于单一外生变量zt变化;υt、μt是服从标准正态分布的新息项;εt可服从厚尾分布以体现经济变量中常出现的极端事件;σt是用时间的连续或间断函数表示的时变波动因子。该模型设定了易扩展至高维模型和多平滑变量的情景。
1.2 时变波动方差的处理
Tu 和Wang(2020)[8]将自适应估计用于含时变波动方差的函数系数协整模型,形如:
提出加权核最小二乘(Weighted KLS)估计,当权重取1σt时估计量为:
其拥有最小方差-协方差矩阵。其中,K(·)=k(·/h)为核函数,h是窗宽。当使用σ2的非参数估计值代替权重时,可得自适应核权最小二乘(Adaptive KLS)估计。
1.3 厚尾特征的处理
Tang 和Wang(2005)[5]研究了含异常值或厚尾特征的函数系数模型:
对于任意z0∈[0,1],在求解系数βj(z0)局部点的估计值时,周边点的系数均用线性函数近似:aj+bj(z-z0)。基于绝对离差之和最小,即最小化式(5)可求系数的逐点估计值:
1.4 改进的估计流程
基于模型(1)构建局部线性ALADE流程。将L1最优化准则引入估计全流程,选择局部线性估计方法,最优窗宽选择采用绝对值交叉验证方法,考虑可行的自适应估计流程以减少时变波动方差的影响。估计流程见图1。
第一,模型的局部线性LADE。将某点的系数值近似为:a0(zt)≈a0+b0(zt-z0),aj(zt)xtj≈ajxtj+bj(zt-z0)xtj,最小化式(7)可得局部线性LADE。
第二,在估计流程的第五步中涉及广义局部线性LADE:
当权重ωt设定为时变方差时(ωt=gt),估计量拥有最小的渐近方差-协方差矩阵。该方法被称为不可行的局部线性ALADE。
第三,可行的局部线性ALADE 的权重选择。文献中常将残差的局部核估计值作为权重的替代值,即:
第四,窗宽的选择。在核估计的过程中,窗宽的选择起决定性作用。异常值的存在导致该点所求的残差平方和将占据主导地位,窗宽的选取将异常困难,此处更适合采用绝对值交叉验证法(ACV)进行窗宽选择。
在流程中涉及三处窗宽选择,窗宽b的选择参考式(10):
窗宽h的选择参考式(11):
2 蒙特卡洛模拟
本文将模拟含时变波动方差和厚尾特征的函数系数协整模型,生成样本数据以分析局部线性ALADE 方法的优劣。考虑下列数据生成过程:
其中,zt服从(-0.5,0.5)上的均匀分布,x1,t、x2,t是初始值为0 的单位根过程。εt分别服从:(1)标准正态分布;(2)位置参数为0、尺度参数为0.2 的柯西分布。g(t/n)为时变波动方差,分三种情形讨论:
情形1 和情形2 代表了时变波动方差的突变形式,情形3 代表了方差的平滑特征。单变点令τ取(0.2,0.8)表示突变点发生在前端和后端;双变点τ和1-τ的取值表示跳跃发生的时间点,令τ取(0.2,0.4)表示两次跳跃发生在序列的两端和中间处;平滑时变特征中令m取(1,2)表示变化快慢。同时令σ0=2,标准差前后变化之比设为δ=σ1/σ0,令δ的取值为(0.2,0.5,1,5)。
样本量分别取200 和400,模拟次数设定为200 次。采用核权最小二乘估计(KLS)、自适应核权最小二乘估计(AKLS)、局部线性LADE(LADE)三种方法做对比,综合分析局部线性ALADE(ALADE)方法的表现。核函数选取二阶EP 核,采用局部线性估计以保证方法间的可比性。
2.1 系数估计情况分析
先分析单次样本数据下四种估计方法对模型系数拟合精度的表现。
当εt~N(0,1)且存在时变波动方差时,基于L2准则的系数估计曲线在各类时变波动情形下更加贴近系数真实值,而基于L1准则的曲线拟合效果较差(图略)。含单变点和双变点的时变波动方差时,(τ,δ)取值为(0.2,0.2)时四种估计方法下的系数均与实际值更加贴近,取值为(0.2,5)时各方法下的系数较实际系数曲线偏离严重。含平滑时变波动方差时,(m,δ)取值为(1,0.2)时各估计方法下的系数均贴合实际曲线,取值为(1,5)时各估计方法下的系数偏离实际系数曲线最大。当不存在时变波动(δ=1)时,AKLS 与KLS 估计的系数曲线基本重合,说明自适应估计和传统估计效果一致,且明显优于ALADE 和LADE。
当εt~C(0,0.2)时,基于L1准则的系数估计曲线更加贴近系数真实值(图略),且ALADE 估计方法在部分情况下优于LADE。含单变点和双变点的时变波动方差时,(τ,δ)取值为(0.2,0.2)时四种估计方法的系数曲线接近且紧贴实际曲线,取值为(0.2,5)时基于L2方法的估计值偏离实际值较大。含平滑时变波动方差时,(m,δ)取值为(1,0.2)时四种估计方法的系数与实际值相近,取值为(1,5)时基于L2方法的系数估计值严重偏离实际系数曲线。
综上,当残差中含厚尾特征且存在时变波动方差时:就系数估计精度而言,ALADE估计和LADE方法优于AKLS方法;并且时变波动方差的存在会影响估计效果,且波动值越大影响越大。
2.2 系数整体拟合精度分析
分析可知,当残差服从柯西分布时,基于L1最优准则的估计系数表现相对较好,但ALADE 方法与LADE 方法间的差异通过图形难以判断。接下来选取加权平均误差(Weighted Average Squared Error,WASE)指标来分析系数整体拟合情况,定义如下:
在模拟过程中,产生200和400的样本数据,并各进行200次蒙特卡洛模拟实验后取WASE的均值和标准差进行对比分析(见表1)。分析发现:第一,对比四种估计方法对系数整体的拟合效果可以发现,LADE和ALADE方法的WASE 的均值明显小于KLS 和AKLS 估计的取值。第二,随着样本的增加,ALADE相比LADE对系数的拟合情况更好:单变点除(τ,δ)取值为(0.8,0.2)外,双变点除δ=0.2 情形外,其他各类情况下ALADE 估计所得WASE 的均值相比LADE 估计值都更小,标准差也很接近且波动较小;含平滑变动时变波动方差的各类情况下,除(m,δ)取值(2,0.2),即方差变小且变动较慢外,其他各类情况下ALADE的WASE的均值均更小。整体而言,当残差来自厚尾分布时,ALADE估计对系数的拟合更好且稳健。
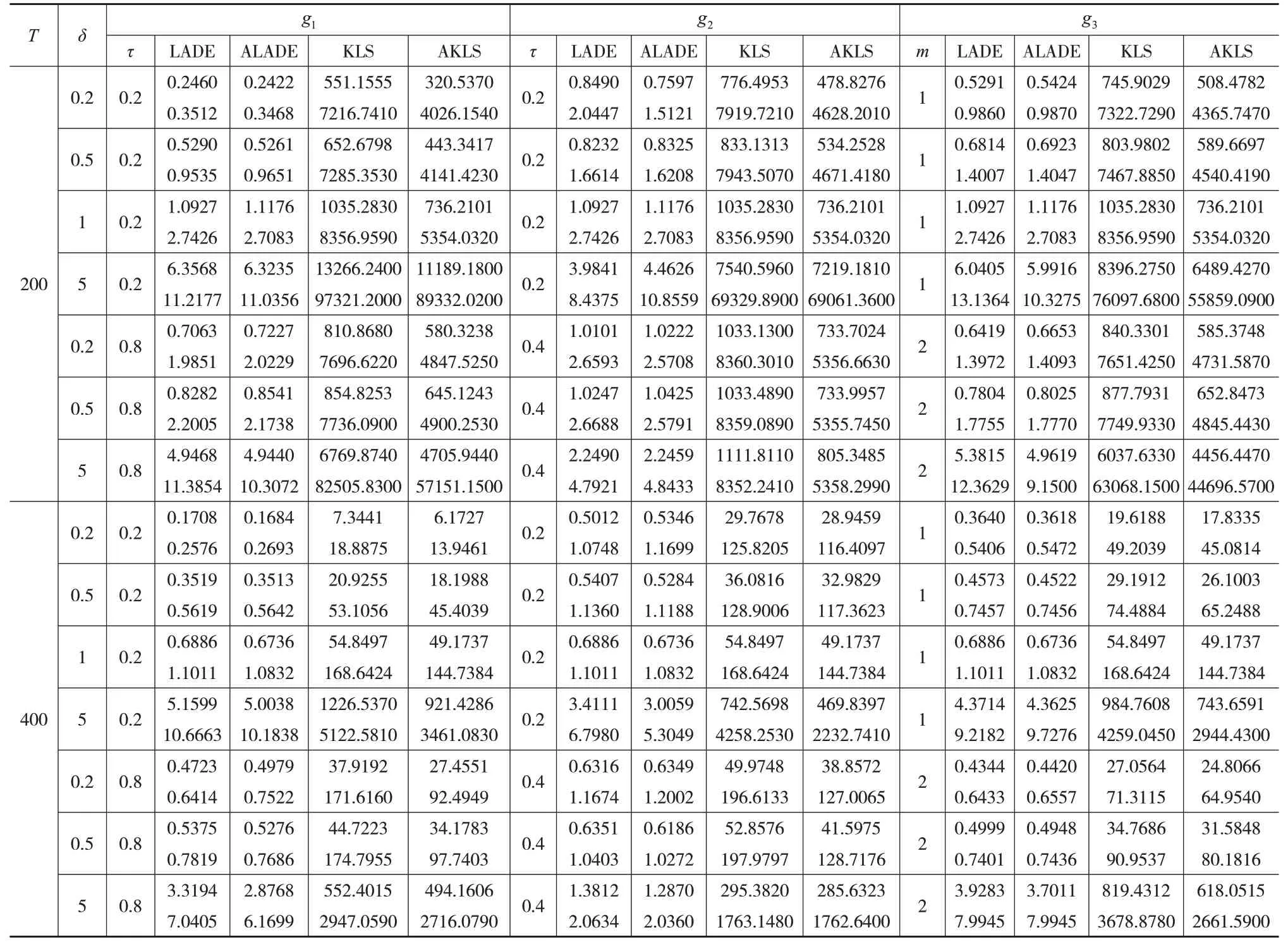
表1 εt~C(0,0.2)时WASE的均值和标准差
接下来,从最优窗宽的角度分析AKLS和ALADE两种估计方法对系数的整体拟合效果,通过分析WASE与窗宽h间的函数曲线图得出结论。限于篇幅,仅展示残差服从柯西分布的部分情形(见下页图2)。
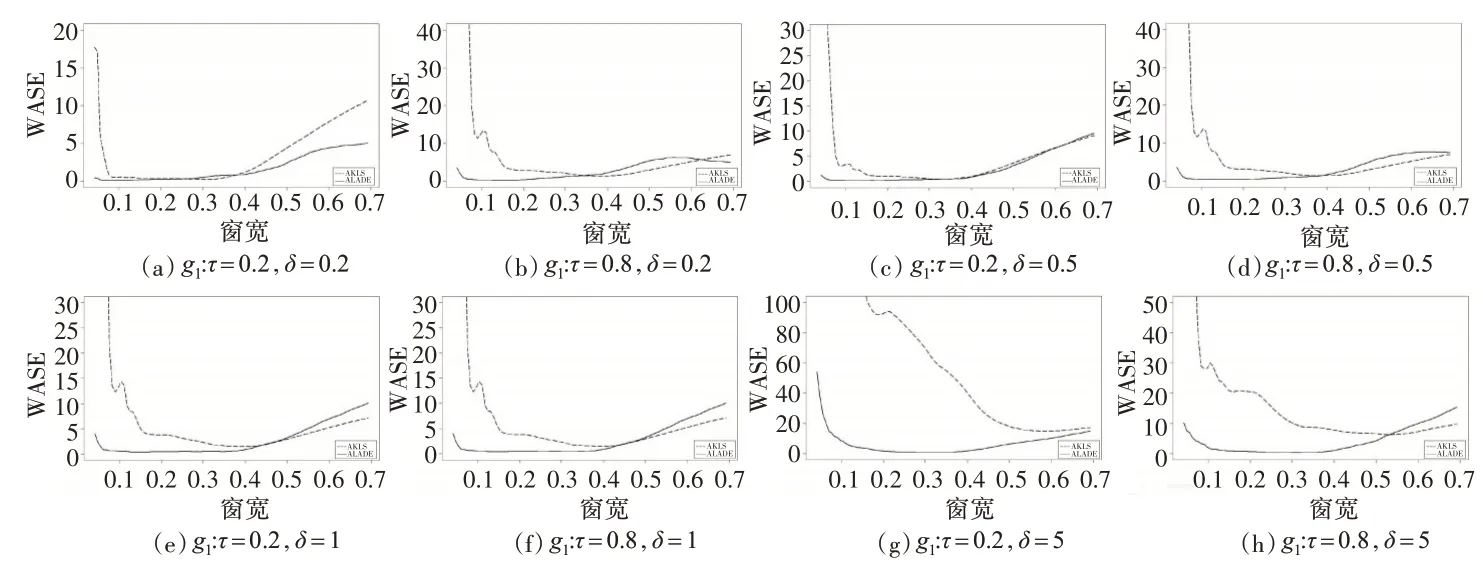
图2 εt~C(0,0.2)及g1 下WASE的窗宽曲线图
由图2 可知,当残差服从柯西分布时,两种估计方法的WASE 曲线在底部区域比较平缓,说明WASE 的取值对h的大小不太敏感,且δ取值越大,AKLS 估计下的WASE 曲线波动也越大。在各时变波动情形下,ALADE估计方法下的曲线低于AKLS 估计下的曲线,说明前者对系数的整体拟合精度更好。随着时变方差前后波动取值变大(δ>1),ALADE 估计的WASE 曲线相比AKLS的曲线更平滑且取值更低。但是,当残差服从正态分布时,AKLS估计下WASE曲线包络ALADE的曲线,对系数拟合更有效。
2.3 模型的整体拟合情况
本文选取均方误差(Mean Squared Error,MSE)来衡量模型偏差和方差的权衡情况。以ALADE 所计算的MSE 均值为基准,计算LADE 方法下MSE 均值的相对值(即MSELADE/MSEALADE)。
分析表2可得,当残差序列含厚尾特征且样本量较小时,ALADE 估计的MSE 均值远小于LADE 方法下的取值。随着样本量的增加,两种估计方法下的MSE 均值差异均变小,整体而言,ALADE方法对模型的整体拟合效果更好,且随着δ的取值变大,ALADE方法的优势更加明显。
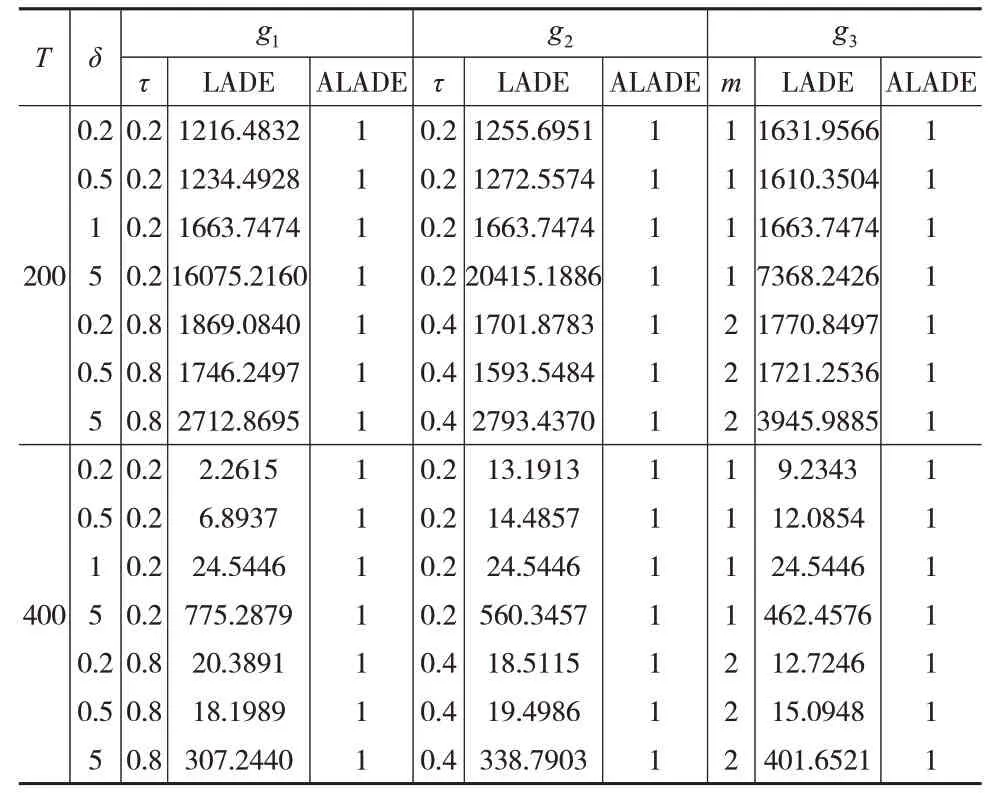
表2 εt~C(0,0.2)时MSE的相对值
综上所述,当残差服从厚尾分布时,基于L1损失函数的估计方法对模型的拟合要整体优于基于L2损失函数的方法。本文提出的局部线性ALADE方法在多数情况下对系数的拟合都更加精准,对模型的整体估计也具有绝对优势,当方差波动越大时表现出越好的稳健性。
2.4 最优窗宽选择方法比较
为了选取适合ALADE流程的窗宽选择方法,接下来分析绝对值交叉验证方法(ACV)和最小二乘交叉验证方法(CV)的表现。ALADE 流程共有三处需要进行最优窗宽选择,分别为LADE估计时的窗宽h1、计算权重估计值时的窗宽b,以及ALADE 估计时的窗宽h2,且均采用ACV 方法。现将三处统一替换为CV方法,比较替换前后两者的表现。本文仅展示求解最优窗宽h2的环节中ACV 和CV 两种窗宽选择方法中取值随窗宽变化的曲线图。纵轴的刻度没有实际意义,仅比较曲线随着窗宽变化的形态。要求曲线的形状随着窗宽的变动呈现平滑的凸性,且存在最小值。
当残差服从正态分布时,ALADE 估计中ACV 方法的表现略优于CV方法,但整体而言两者均为求解最优窗宽带来困难(图略)。下页图3 呈现了残差服从柯西分布时的表现。分析可知:ACV曲线在不同波动情况下均表现为一条较为平滑的凸性曲线,求解最优值明显且唯一,且随着δ取值越大,图形的凸性越明显。CV 曲线对h的取值不敏感;随着δ的取值变大,底部呈现“W”型波动形态,最优值不唯一。故ALADE 估计中的ACV 方法在各种时变波动情形下均优于CV方法。
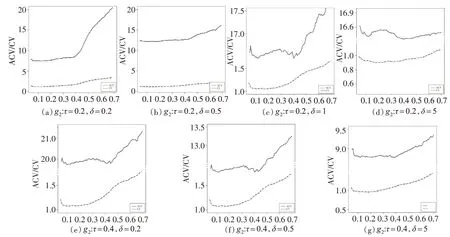
图3 εt~C(0,0.2)及g2 下ACV/CV随窗宽变化图
综合分析KLS、AKLS、LADE以及ALADE四种估计方法的系数拟合曲线、系数估计精度平均表现、模型整体拟合效果以及窗宽选择方法的优劣后发现,当FCCM含厚尾特征和时变波动方差时,可行的局部线性自适应LADE方法在大多数情况下都表现出了明显优势,且估计流程中ACV方法更适合进行最优窗宽选择。
3 实证分析
购买力平价理论(Theory of Purchasing Power Parity,简称PPP 理论)提供了相对价格关系间的客观比较,能反映经济发展水平和价格水平所具有的本质联系。现利用函数系数协整模型对中英两国PPP 理论的有效性进行再检验,模型构建如下:
变量定义和数据来源见下页表3。参考Tu 和Wang(2020)[8]的描述,zt选用两国间收益率之差(简称利差)表示,定义zt=(T10Y,C,t-T5Y,C,t)-(T10Y,U,t-T5Y,U,t)。根据建模前的相关分析可知:EXt、Pt、序列中均含有突变点且含厚尾特征,原序列通过方差比检验[10]均被确定为单位根过程,可构建函数系数协整模型。
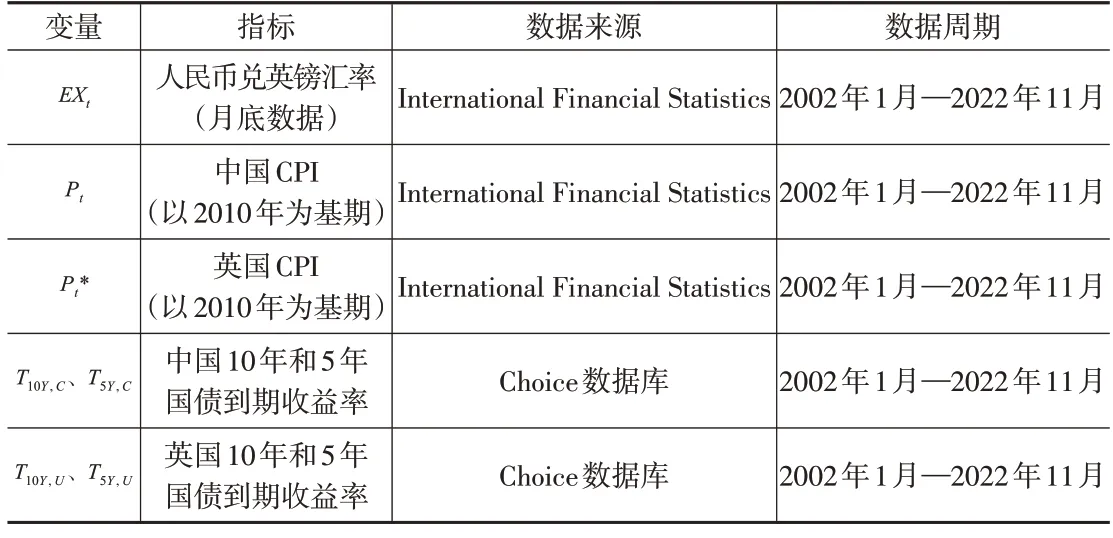
表3 变量选取说明
3.1 参照方法的估计结果
为了清晰地展示ALADE估计流程的优势,现梳理其他四种常用估计方法作为参照,分别是:传统核权最小二乘估计(KLS)、对局部常数(LC)和局部线性(LL)估计分别进行讨论、Tu 和Wang(2020)[8]提出的自适应核权最小二乘估计(AKLS)、Feng等(2012)[6]提出的最小绝对离差估计(LADE)。
使用KLS+LC、KLS+LL、AKLS、LADE四种方法对模型进行估计,核函数均采用二阶EP 核。选用方差比检验对估计后的残差进行平稳性检验,结果见表4,同时结合方差轮廓图[11]以及Wu 和Xiao(2018)[12]提出的U 统计量对是否含时变波动方差进行分析,当这两种方法都判定为同方差时,认为序列不含时变波动方差。

表4 残差检验结果
经检验,四种估计方法得到的残差均平稳,证明变量间的复杂协整关系成立。U 统计量的结果和方差轮廓图(见图4)显示,四种方法拟合后,残差中均存在明显的时变波动性,会影响估计效率。
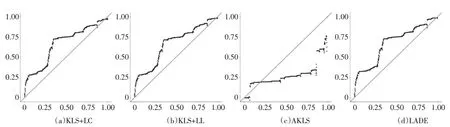
图4 方差轮廓图
两国间PPP 理论是否有效还需关注系数是否满足理论要求。下页图5给出了四种估计方法下Pt和的系数随利差的变动曲线图。分析可知,局部常数KLS 估计和局部线性KLS 估计下两国汇率和价格之差间的协整关系存在,但系数估计值偏离理论值较大,且残差中含时变波动性。AKLS估计的系数估计值与理论值完全不符,判定中英两国间PPP 理论非有效。LADE 估计方法证实序列间协整关系存在,但是系数随利差波动出现偏离理论值和异常波动的情况,且残差中含时变波动性。
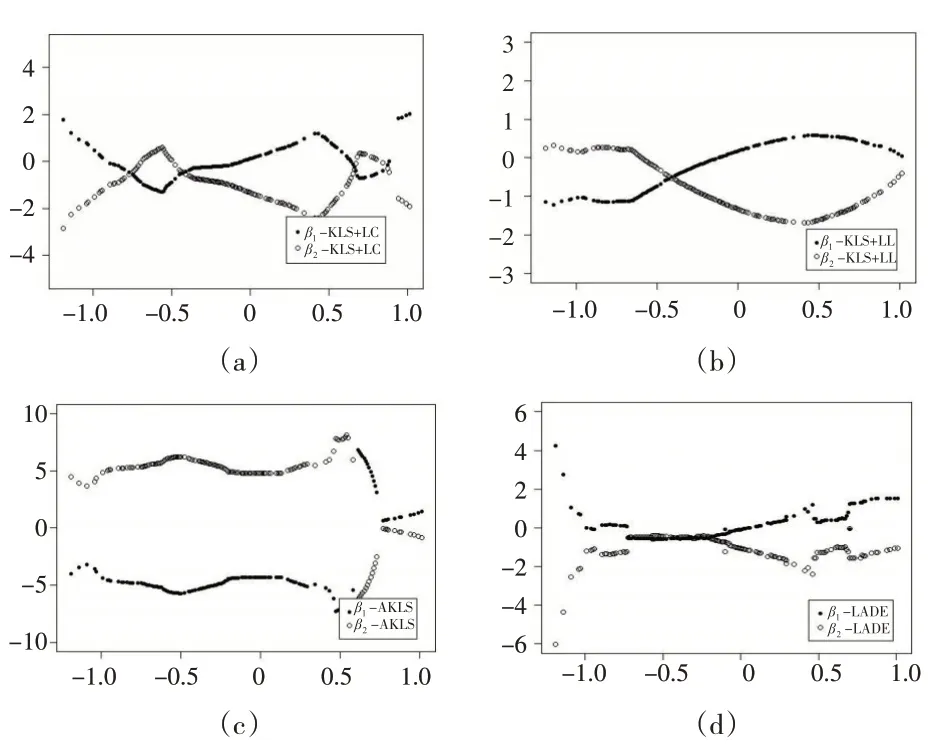
图5 不同方法下系数估计值随利差变动曲线图
3.2 ALADE流程估计结果
采用ALADE方法对模型(14)进行估计,估计后各类检验结果整理为表5。

表5 ALADE估计结果
将估计后残差序列的非参数估计值作为时变波动方差的替代值,窗宽b取值很小使得局部平滑估计值参考周边邻点的信息较少,更加贴近残差真实值。将非参数估计值作为权重代入ALADE 方法进行估计,最优窗宽h2取值适中,既能体现每个时点的波动特征,又能得到相对平滑的系数估计值。ALADE估计后模型的残差序列经检验为平稳序列。经U统计量和方差轮廓图(图略)证实,模型残差中不存在时变波动方差。中英两国汇率和价差间的协整关系成立。
下页图6 为系数估计值随利差变动曲线图。分析后发现,ALADE方法对模型系数的拟合表现较为出色,图形大部分取值围绕±1波动,更符合PPP理论的要求。
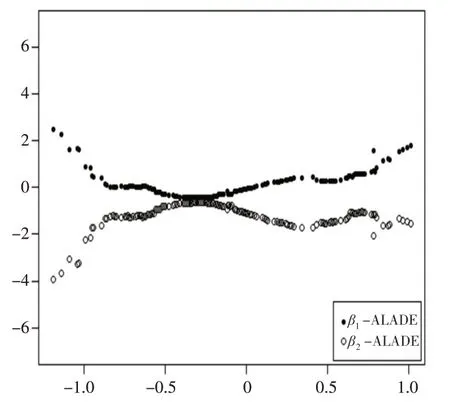
图6 系数估计值随利差变动曲线图(ALADE)
综上,中英两国汇率和价差序列所建模型中确实含时变波动方差和厚尾特征。通过ALADE方法进行估计和验证后,证实了中英两国PPP 理论的有效性,且系数的估计曲线随利差平滑变动,估计效果稳健且有效。
4 结论
函数系数协整模型被应用于复杂经济问题的研究时,当存在时变波动方差和厚尾特征时,估计量不再有效。本文考虑了此类特征后,提出局部线性自适应最小绝对离差估计(ALADE)流程。
本文所提方法在系数估计精度、整体拟合效果、窗宽最优选择等方面都表现优异,分析发现,ACV方法更适用于此类建模中的最优窗宽选择。实证分析部分将局部线性ALADE流程应用于中英两国PPP理论的建模分析,拟合后的残差平稳且不存在时变波动特征,系数更稳健且符合理论要求,最终证实了PPP 理论的有效性。
